7.5 多边形的内角和和外角和(第2课时)(共43张PPT)
文档属性
| 名称 | 7.5 多边形的内角和和外角和(第2课时)(共43张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 00:00:00 | ||
图片预览







文档简介
7.5 多边形的内角和和外角和
第2课时
第7章 平面图形的认识(二)
2020-2021学年度苏科版七年级下册
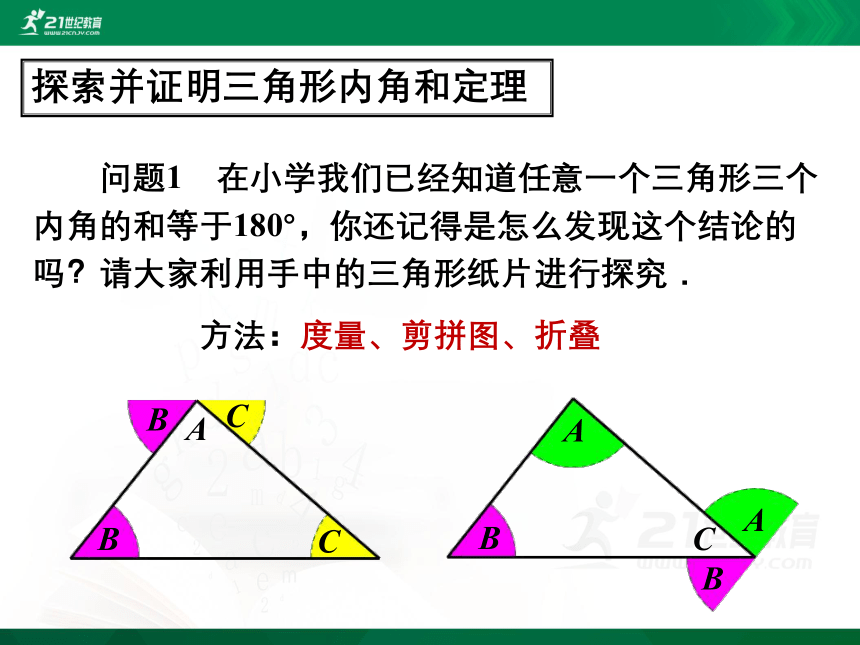
方法:度量、剪拼图、折叠
探索并证明三角形内角和定理
B
B
C
C
A
A
A
B
B
C
问题1 在小学我们已经知道任意一个三角形三个
内角的和等于180°,你还记得是怎么发现这个结论的
吗?请大家利用手中的三角形纸片进行探究.
问题1 在小学我们已经知道任意一个三角形三个
内角的和等于180°,你还记得是怎么发现这个结论的
吗?请大家利用手中的三角形纸片进行探究.
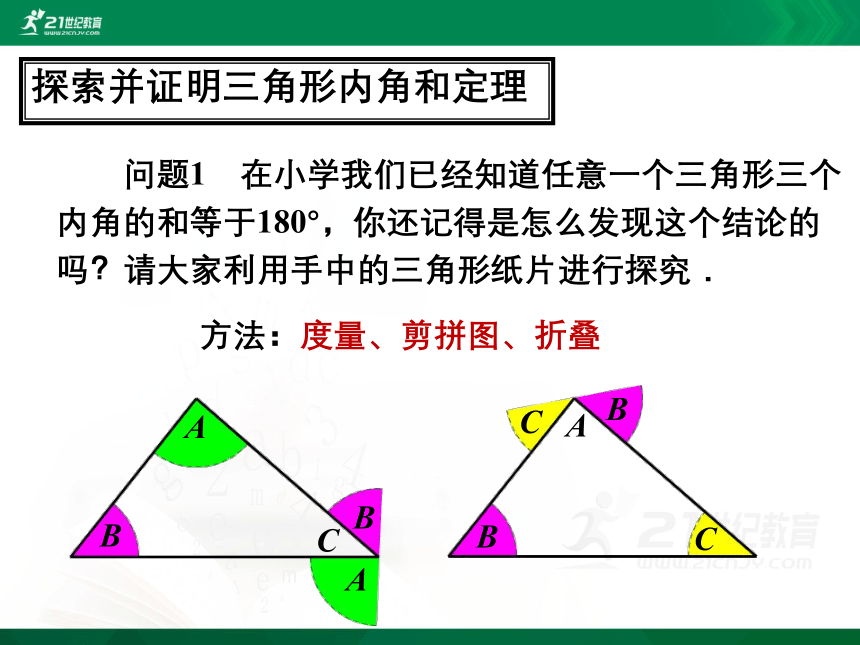
探索并证明三角形内角和定理
A
A
B
B
C
A
B
B
C
C
方法:度量、剪拼图、折叠
问题1 在小学我们已经知道任意一个三角形三个
内角的和等于180°,你还记得是怎么发现这个结论的
吗?请大家利用手中的三角形纸片进行探究.
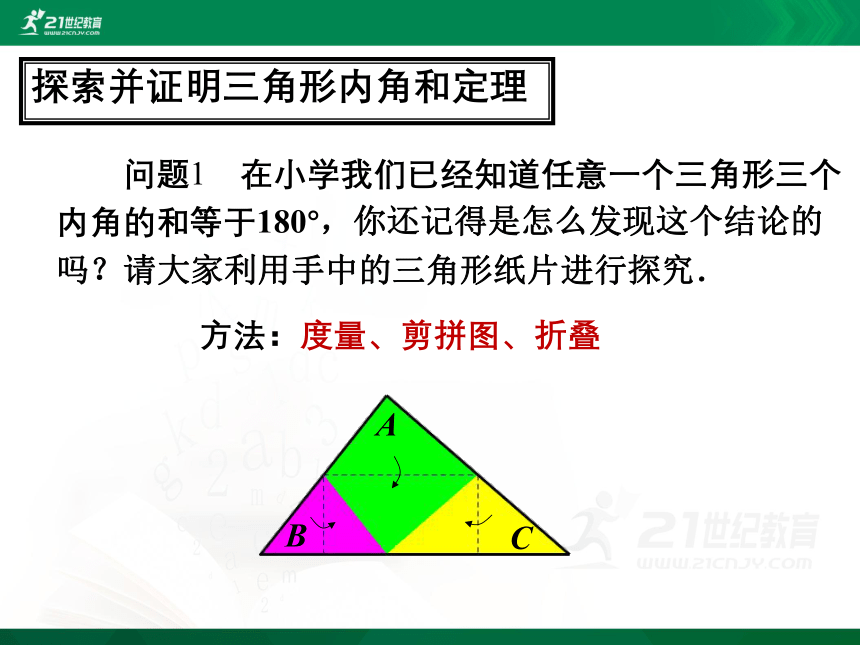
探索并证明三角形内角和定理
A
B
C
方法:度量、剪拼图、折叠
探索并证明三角形内角和定理
追问1 运用度量的方法,得出的三个内角的和都
是180°吗?为什么?
测量可能会有误差.
探索并证明三角形内角和定理
追问2 通过度量、剪拼图或折叠的方法验证了手
中的三角形纸片的三个内角和等于180°,但我们手中
的三角形只是所有三角形中有限的几个,而形状不同的
三角形有无数多个,我们如何能得出“所有的三角形的
三个内角的和都等于180°”这个结论呢?
需要通过推理的方法去证明.
2
1
E
D
C
B
A
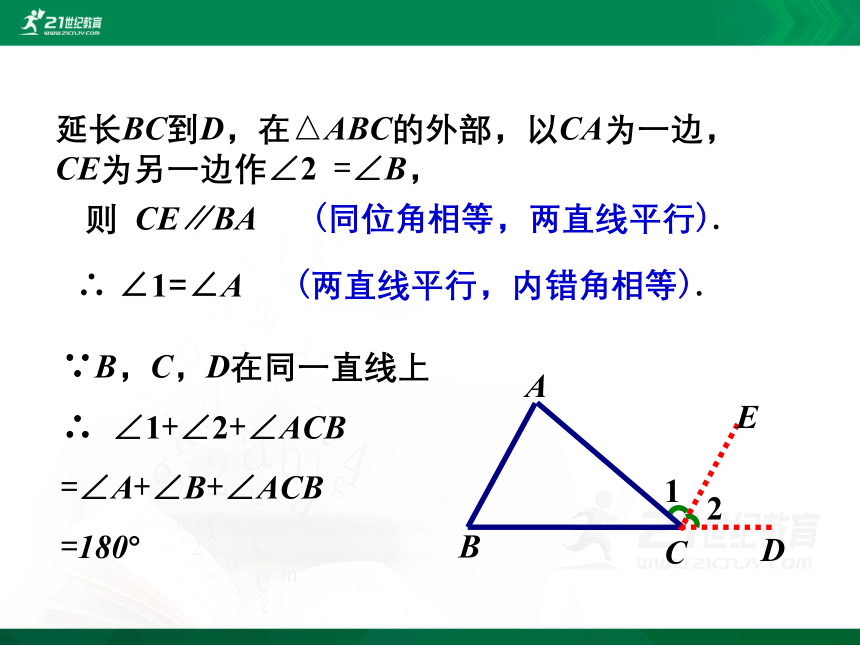
则 CE∥BA
(同位角相等,两直线平行).
∴ ∠1=∠A
(两直线平行,内错角相等).
∵B,C,D在同一直线上
∴ ∠1+∠2+∠ACB
=∠A+∠B+∠ACB
=180°
延长BC到D,在△ABC的外部,以CA为一边,
CE为另一边作∠2 =∠B,
例1 在△ABC中,∠A=40 ° ,∠B=∠C.求∠C的度数.
解:在△ABC,
由∠A+∠B+∠C=180 ° ,∠A=40 ° ,得
∠B+∠ C=180 °-∠A=180 ° -40 ° =140 °.
由∠ B=∠C,得
2∠C=140 ° ,∠C=70 °.
例题讲解
例2 如图7-30,△ABC的角平分线BD、CE相交于点P.∠A=70°.求∠BPC的度数.
解:在△ABC中,
由∠A+∠ABC+∠ACB=180 ° ,∠A=70 °,得
∠ABC+∠ACB=180 °-∠A=180 ° -70 ° =110 ° .
因为BD、CE分别平分∠ABC、∠ACB,
所以∠1= ∠ABC, ∠2= ∠ACB,
∠1+∠2= (∠ABC+ ∠ACB)= ×110 °=55 °.
在△PBC中,
由∠BPC+∠1+∠2=180 ° ,∠1+∠2=55 ° ,得
∠BPC=180 ° -(∠1+∠2)=180 °-55 ° =125 °.
例题讲解
在同一平面内,由一些线段首尾顺次连接而成的图形,
2.多边形可分为___________和__________两类.
3._________________________叫多边形的对角线.
1._______________________________叫多边形.
凸多边形
凹多边形
多边形不相邻的顶点的连线
你都知道吗?
2.长方形、正方形的内角和都是______.
3.任意四边形的内角和是360°吗?你
能用哪些方法说明?
1.三角形的内角和是________.
180°
360°
合作探究:小组讨论,有哪些方法可知道四边形内角和是多少?
A
B
C
D
A
B
C
D
B
C
D
A
A
B
D
C
E
小结方法
综合这几种方法,其共同点是什么?
从一个点出发和各顶点相连,把四边形的问题转化为三角形的问题.
转化
思想
请你选择一种简单的方法,分别求出任意的五边形、六边形、七边形的内角和.
A
E
D
C
B
五边形内角和为:180°×3=540°.
六边形内角和为:180°×4=720°.
B
C
D
E
F
D
C
B
A
E
F
G
A
七边形内角和为:180°×5=900°.
任意六边形内角和、七边形内角和
多边形
的边数
图形
多边形的
内角和
3
4
5
6
------
------
------
------
n
n-2
1
2
3
1×180?=180?
从一个顶点出发分割成的三角形个数
2×180?=360?
3×180?=540?
(n-2)×180?
4
4×180?=720?
n边形的内角和等于
(n-2)·180°.
多边形的内角和公式:
这里的字母n是指大于或等于3的整数.
解: ∠ B与∠D互补.
在四边形ABCD中,
∠A+∠B+∠C+∠D=(4-2) × 180 ° =360 °.
由∠A+∠C=180 ° ,得
∠B+∠D=360 ° -(∠A+∠C)=360 ° -180 ° =180 °,
即∠B与∠D互补.
例3 如图7-35,在四边形ABCD中,∠A与∠C互补.∠B与∠D有怎样的数量关系?为什么?
在2008年北京奥运会会徽征集的时候,小明曾想:设计一个内角和为2008°的多边形图案多有纪念意义呀,小明的想法能做到吗?
开动脑筋
小明的想法不能做到,因为多边形的边数必须是大于或等于3的正整数.
已知一个多边形,它的内角和等于五边形的内角和的2倍,求这个多边形的边数.
解:设边数为n,则可列方程为:
(n-2)×180°=(5-2)×180°×2
解得n=8,
所以这个多边形的边数是八.
方程
思想
一、n边形的内角和公式:
二、几种数学思想:
(n-2)·180°
转化思想、方程思想.
方法一:
180×2=360.
A
B
C
D
A
B
D
C
B
D
A
C
B
D
O
方法二:
180×4-360=360.
D
C
D
C
B
B
A
A
O
方法三:
180×3-180=360.
A
B
C
D
E
A
B
E
A
D
E
C
E
D
探索多边形的内角和与外角和
多边形内角的一边与________________所组成的角叫做这个多边形的外角.在每个顶点处取这个多边形的一个外角,它们的和叫做__________.
快速反应
(1)x=180°-81°-72°=27°;
(2)y=180°-90°-31°=59°.
1.求图中x和y的值.
2.如图,铅笔放置在△ABC的边AB上,笔尖方向为点A到点B的方向.把铅笔依次绕点A、点C、点B按逆时针方向旋转∠A、∠C、∠B的度数,笔尖方向发生了怎样的变化?这种变化说明了什么?
解:笔尖方向变为点B到点A的方向.说明三角形内角和等于180°.
3.一个三角形能有两个内角是直角或钝角吗?为什么?
解:不能.因为有两个内角是直角或钝角后其内角和就会大于180°,所以不能有.
探索多边形的外角和
怎样求三角形的外角和?
思考
四边形的外角和呢?
五边形的外角和呢?
探索多边形的外角和:
任意多边形的外角和都为360°.
多边形的边数
3
4
5
6
…
n
多边形的内角与外角的总和
…
多边形的内角和
…
多边形的外角和
…
540°
720°
900°
1080°
180°
360°
540°
720°
360°
360°
360°
360°
n×180°
(n-2×180°
360°
一个多边形的每个外角都是72°,这个多边形是几边形?
解:设多边形的变数是n,根据题意,得
n?72°=360°.
解得:n=5.
因此,这个多边形是五边形.
1、有一个正多边形的外角是60°,那么该正多边形是正___________边形.
快速反应
2、有一个多边形的内角和是它的外角和的3倍,那么该多边形的边数是____________.
1、一个多边形的每个内角都比邻外角的3倍还多20度,求这个多边形的边数.
自主学习
2、如果一个多边形的每一个外角都相等,并且小于45度,那么这个多边形的边数最少是多少?
3、已知四边形四个外角的度数之比分别为8:6:3:7.求四边形四个内角的度数分别是多少?
开动脑筋
若多边形的所有内角与它的一个外角的和为600°,求这个多边形的边数和内角和.
练习
填空:
(1)十边形的内角和是________,
外角和是_________;
如果十边形的各个内角都相等,
那么它的一个内角是_________.
1440°
360°
144°
(1)x=(360°-90°-150°)/2=60°;
(2)y=(540°-90°-150°-120°)/3=60°.
1.求图中x和y的值.
2.如图,六边形ABCDEF的内角都相等,求它的每个内角的度数.
解:(6-2) ×180°/6=120°.
3.一个多边形的内角和为1080°,这个多边形是几边形?
解:1080°/180°+2=8.
这个多边形是八边形.
小明转过的角度总共是360°,这说明了多边形外角和等于360°.
1.如图,S是六边形草地ABCDEF的边AB上一点.小明从点S出发,沿着它的边步行l周回到点S处.小明转过的角度总共是多少?这说明了什么?
2.在一个多边形中,小于108°的内角最多
有几个?为什么?
解:
要使内角小于108°,则就要使它对应的外角大于180°-108°=72°,我们知道,在凸多边形中,外角和总为360°,因为360°÷72°=5,所以最多只能有4个外角大于72°的,即小于108°的内角最多有4个.
谢谢聆听
第2课时
第7章 平面图形的认识(二)
2020-2021学年度苏科版七年级下册
方法:度量、剪拼图、折叠
探索并证明三角形内角和定理
B
B
C
C
A
A
A
B
B
C
问题1 在小学我们已经知道任意一个三角形三个
内角的和等于180°,你还记得是怎么发现这个结论的
吗?请大家利用手中的三角形纸片进行探究.
问题1 在小学我们已经知道任意一个三角形三个
内角的和等于180°,你还记得是怎么发现这个结论的
吗?请大家利用手中的三角形纸片进行探究.
探索并证明三角形内角和定理
A
A
B
B
C
A
B
B
C
C
方法:度量、剪拼图、折叠
问题1 在小学我们已经知道任意一个三角形三个
内角的和等于180°,你还记得是怎么发现这个结论的
吗?请大家利用手中的三角形纸片进行探究.
探索并证明三角形内角和定理
A
B
C
方法:度量、剪拼图、折叠
探索并证明三角形内角和定理
追问1 运用度量的方法,得出的三个内角的和都
是180°吗?为什么?
测量可能会有误差.
探索并证明三角形内角和定理
追问2 通过度量、剪拼图或折叠的方法验证了手
中的三角形纸片的三个内角和等于180°,但我们手中
的三角形只是所有三角形中有限的几个,而形状不同的
三角形有无数多个,我们如何能得出“所有的三角形的
三个内角的和都等于180°”这个结论呢?
需要通过推理的方法去证明.
2
1
E
D
C
B
A
则 CE∥BA
(同位角相等,两直线平行).
∴ ∠1=∠A
(两直线平行,内错角相等).
∵B,C,D在同一直线上
∴ ∠1+∠2+∠ACB
=∠A+∠B+∠ACB
=180°
延长BC到D,在△ABC的外部,以CA为一边,
CE为另一边作∠2 =∠B,
例1 在△ABC中,∠A=40 ° ,∠B=∠C.求∠C的度数.
解:在△ABC,
由∠A+∠B+∠C=180 ° ,∠A=40 ° ,得
∠B+∠ C=180 °-∠A=180 ° -40 ° =140 °.
由∠ B=∠C,得
2∠C=140 ° ,∠C=70 °.
例题讲解
例2 如图7-30,△ABC的角平分线BD、CE相交于点P.∠A=70°.求∠BPC的度数.
解:在△ABC中,
由∠A+∠ABC+∠ACB=180 ° ,∠A=70 °,得
∠ABC+∠ACB=180 °-∠A=180 ° -70 ° =110 ° .
因为BD、CE分别平分∠ABC、∠ACB,
所以∠1= ∠ABC, ∠2= ∠ACB,
∠1+∠2= (∠ABC+ ∠ACB)= ×110 °=55 °.
在△PBC中,
由∠BPC+∠1+∠2=180 ° ,∠1+∠2=55 ° ,得
∠BPC=180 ° -(∠1+∠2)=180 °-55 ° =125 °.
例题讲解
在同一平面内,由一些线段首尾顺次连接而成的图形,
2.多边形可分为___________和__________两类.
3._________________________叫多边形的对角线.
1._______________________________叫多边形.
凸多边形
凹多边形
多边形不相邻的顶点的连线
你都知道吗?
2.长方形、正方形的内角和都是______.
3.任意四边形的内角和是360°吗?你
能用哪些方法说明?
1.三角形的内角和是________.
180°
360°
合作探究:小组讨论,有哪些方法可知道四边形内角和是多少?
A
B
C
D
A
B
C
D
B
C
D
A
A
B
D
C
E
小结方法
综合这几种方法,其共同点是什么?
从一个点出发和各顶点相连,把四边形的问题转化为三角形的问题.
转化
思想
请你选择一种简单的方法,分别求出任意的五边形、六边形、七边形的内角和.
A
E
D
C
B
五边形内角和为:180°×3=540°.
六边形内角和为:180°×4=720°.
B
C
D
E
F
D
C
B
A
E
F
G
A
七边形内角和为:180°×5=900°.
任意六边形内角和、七边形内角和
多边形
的边数
图形
多边形的
内角和
3
4
5
6
------
------
------
------
n
n-2
1
2
3
1×180?=180?
从一个顶点出发分割成的三角形个数
2×180?=360?
3×180?=540?
(n-2)×180?
4
4×180?=720?
n边形的内角和等于
(n-2)·180°.
多边形的内角和公式:
这里的字母n是指大于或等于3的整数.
解: ∠ B与∠D互补.
在四边形ABCD中,
∠A+∠B+∠C+∠D=(4-2) × 180 ° =360 °.
由∠A+∠C=180 ° ,得
∠B+∠D=360 ° -(∠A+∠C)=360 ° -180 ° =180 °,
即∠B与∠D互补.
例3 如图7-35,在四边形ABCD中,∠A与∠C互补.∠B与∠D有怎样的数量关系?为什么?
在2008年北京奥运会会徽征集的时候,小明曾想:设计一个内角和为2008°的多边形图案多有纪念意义呀,小明的想法能做到吗?
开动脑筋
小明的想法不能做到,因为多边形的边数必须是大于或等于3的正整数.
已知一个多边形,它的内角和等于五边形的内角和的2倍,求这个多边形的边数.
解:设边数为n,则可列方程为:
(n-2)×180°=(5-2)×180°×2
解得n=8,
所以这个多边形的边数是八.
方程
思想
一、n边形的内角和公式:
二、几种数学思想:
(n-2)·180°
转化思想、方程思想.
方法一:
180×2=360.
A
B
C
D
A
B
D
C
B
D
A
C
B
D
O
方法二:
180×4-360=360.
D
C
D
C
B
B
A
A
O
方法三:
180×3-180=360.
A
B
C
D
E
A
B
E
A
D
E
C
E
D
探索多边形的内角和与外角和
多边形内角的一边与________________所组成的角叫做这个多边形的外角.在每个顶点处取这个多边形的一个外角,它们的和叫做__________.
快速反应
(1)x=180°-81°-72°=27°;
(2)y=180°-90°-31°=59°.
1.求图中x和y的值.
2.如图,铅笔放置在△ABC的边AB上,笔尖方向为点A到点B的方向.把铅笔依次绕点A、点C、点B按逆时针方向旋转∠A、∠C、∠B的度数,笔尖方向发生了怎样的变化?这种变化说明了什么?
解:笔尖方向变为点B到点A的方向.说明三角形内角和等于180°.
3.一个三角形能有两个内角是直角或钝角吗?为什么?
解:不能.因为有两个内角是直角或钝角后其内角和就会大于180°,所以不能有.
探索多边形的外角和
怎样求三角形的外角和?
思考
四边形的外角和呢?
五边形的外角和呢?
探索多边形的外角和:
任意多边形的外角和都为360°.
多边形的边数
3
4
5
6
…
n
多边形的内角与外角的总和
…
多边形的内角和
…
多边形的外角和
…
540°
720°
900°
1080°
180°
360°
540°
720°
360°
360°
360°
360°
n×180°
(n-2×180°
360°
一个多边形的每个外角都是72°,这个多边形是几边形?
解:设多边形的变数是n,根据题意,得
n?72°=360°.
解得:n=5.
因此,这个多边形是五边形.
1、有一个正多边形的外角是60°,那么该正多边形是正___________边形.
快速反应
2、有一个多边形的内角和是它的外角和的3倍,那么该多边形的边数是____________.
1、一个多边形的每个内角都比邻外角的3倍还多20度,求这个多边形的边数.
自主学习
2、如果一个多边形的每一个外角都相等,并且小于45度,那么这个多边形的边数最少是多少?
3、已知四边形四个外角的度数之比分别为8:6:3:7.求四边形四个内角的度数分别是多少?
开动脑筋
若多边形的所有内角与它的一个外角的和为600°,求这个多边形的边数和内角和.
练习
填空:
(1)十边形的内角和是________,
外角和是_________;
如果十边形的各个内角都相等,
那么它的一个内角是_________.
1440°
360°
144°
(1)x=(360°-90°-150°)/2=60°;
(2)y=(540°-90°-150°-120°)/3=60°.
1.求图中x和y的值.
2.如图,六边形ABCDEF的内角都相等,求它的每个内角的度数.
解:(6-2) ×180°/6=120°.
3.一个多边形的内角和为1080°,这个多边形是几边形?
解:1080°/180°+2=8.
这个多边形是八边形.
小明转过的角度总共是360°,这说明了多边形外角和等于360°.
1.如图,S是六边形草地ABCDEF的边AB上一点.小明从点S出发,沿着它的边步行l周回到点S处.小明转过的角度总共是多少?这说明了什么?
2.在一个多边形中,小于108°的内角最多
有几个?为什么?
解:
要使内角小于108°,则就要使它对应的外角大于180°-108°=72°,我们知道,在凸多边形中,外角和总为360°,因为360°÷72°=5,所以最多只能有4个外角大于72°的,即小于108°的内角最多有4个.
谢谢聆听
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
