7.5 多边形的内角和和外角和(第1课时)(共36张PPT)
文档属性
| 名称 | 7.5 多边形的内角和和外角和(第1课时)(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 00:00:00 | ||
图片预览







文档简介
第1课时
7.5 多边形的内角和和外角和
第7章 平面图形的认识(二)
2020-2021学年度苏科版七年级下册
在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结.可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?” 老二很纳闷.
同学们,你们知道其中的道理吗?
内角三兄弟之争
新课导入
三角形三个内角的和等于
已知:△ABC.
求证:∠A +∠B +∠C=180°
180°
命题的正确性还要严密的推理证明
想一想:如何证明呢?
三角形内角和定理:
2
1
E
D
C
B
A
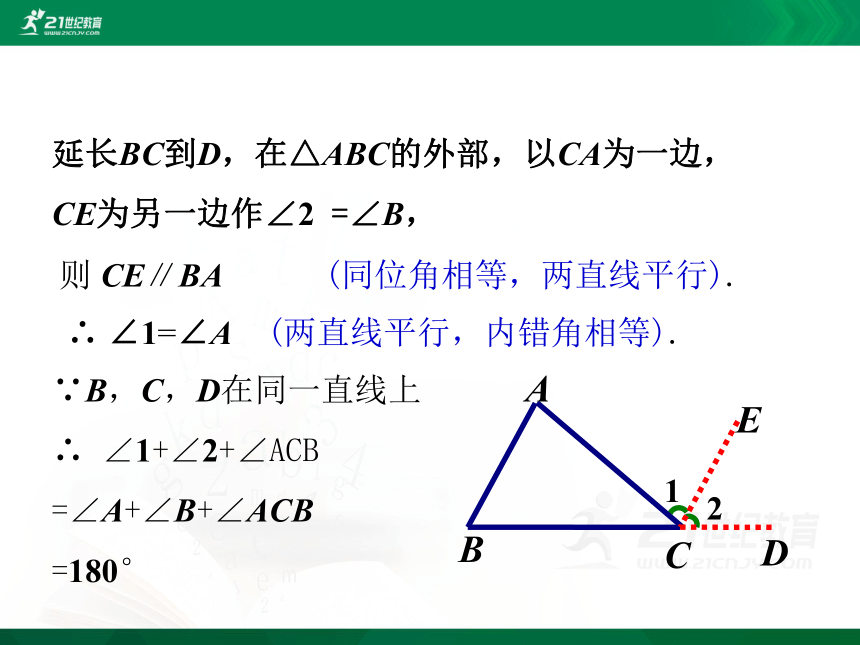
则 CE∥BA
(同位角相等,两直线平行).
∴ ∠1=∠A
(两直线平行,内错角相等).
∵B,C,D在同一直线上
∴ ∠1+∠2+∠ACB
=∠A+∠B+∠ACB
=180°
延长BC到D,在△ABC的外部,以CA为一边,
CE为另一边作∠2 =∠B,
例1 在△ABC中,∠A=40 ° ,∠B=∠C.求∠C的度数.
解:在△ABC,
由∠A+∠B+∠C=180 ° ,∠A=40 ° ,得
∠B+∠ C=180 °-∠A=180 ° -40 ° =140 °.
由∠ B=∠C,得
2∠C=140 ° ,∠C=70 °.
例2 如图7-30,△ABC的角平分线BD、CE相交于点P.∠A=70°.求∠BPC的度数.
解:在△ABC中,
由∠A+∠ABC+∠ACB=180 ° ,∠A=70 °,得
∠ABC+∠ACB=180 °-∠A=180 ° -70 ° =110 ° .
因为BD、CE分别平分∠ABC、∠ACB,
所以∠1= ∠ABC, ∠2= ∠ACB,
∠1+∠2= (∠ABC+ ∠ACB )= ×110 °=55 °.
在△PBC中,
由∠BPC+∠1+∠2=180 ° ,∠1+∠2=55 ° ,得
∠BPC=180 ° -(∠1+∠2)=180 °-55 ° =125 °.
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
为了证明三个角的和为1800,可以转化为一个平角,这种转化思想是数学中的常用方法.
比
一
比
?
1、你能说出什么叫四边形、五边形、多边形吗?
由n条不在同一直线上的线段首尾顺次连结组成的平面图形,称为n边形.
又称为多边形.
问题1:
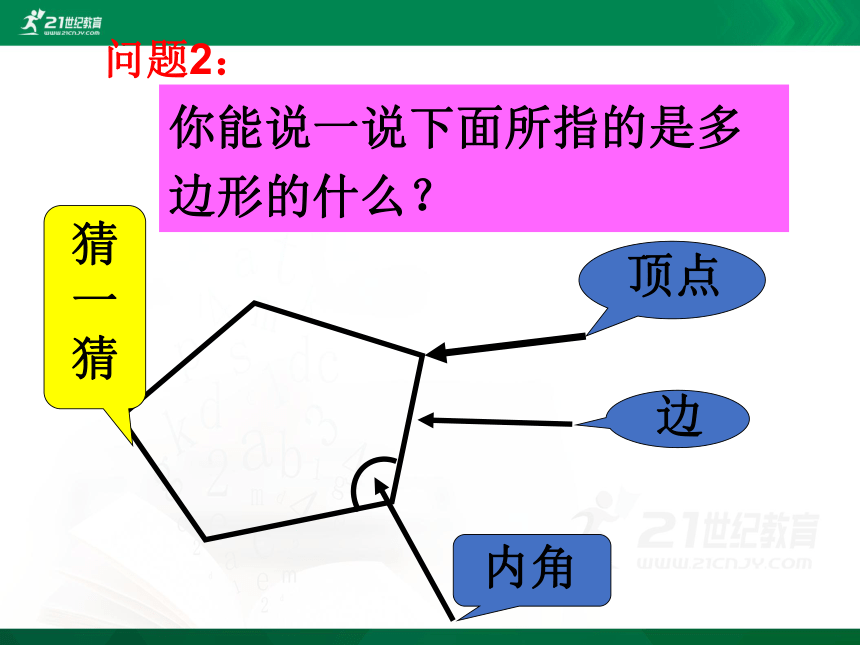
你能说一说下面所指的是多边形的什么?
猜一猜
边
内角
顶点
问题2:
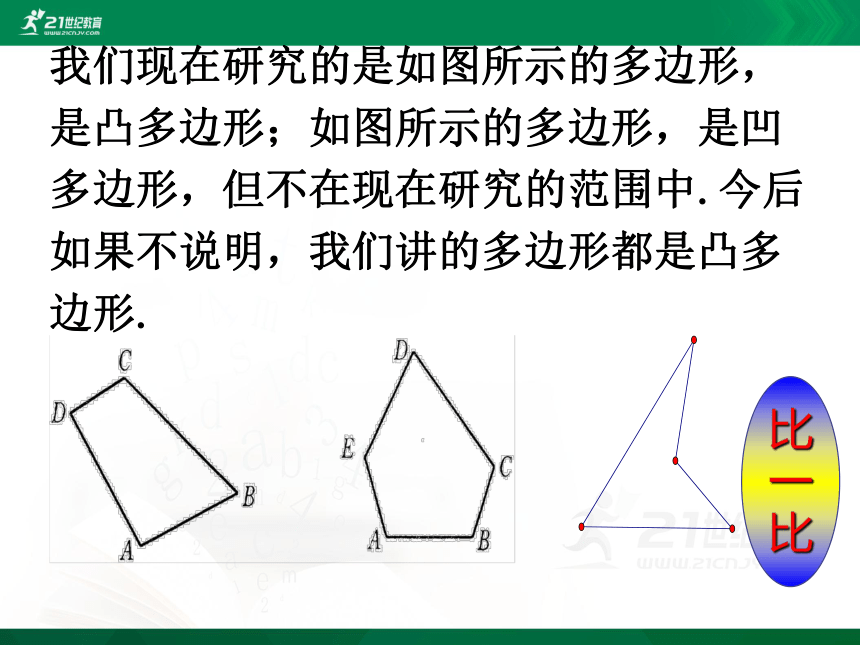
我们现在研究的是如图所示的多边形,是凸多边形;如图所示的多边形,是凹多边形,但不在现在研究的范围中.今后如果不说明,我们讲的多边形都是凸多边形.
比
一
比
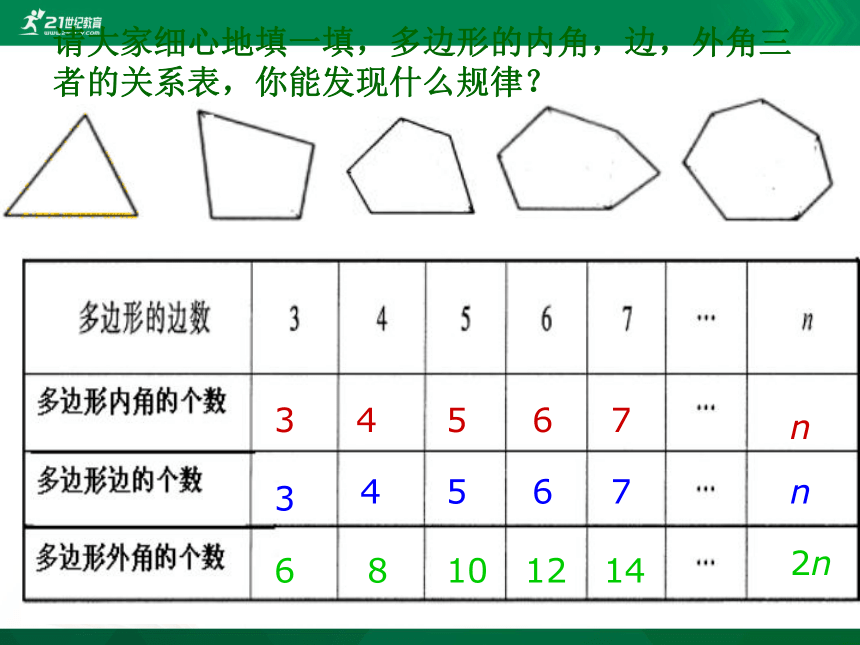
请大家细心地填一填,多边形的内角,边,外角三者的关系表,你能发现什么规律?
3
3
4
4
5
5
6
6
7
7
n
n
6
8
10
12
14
2n
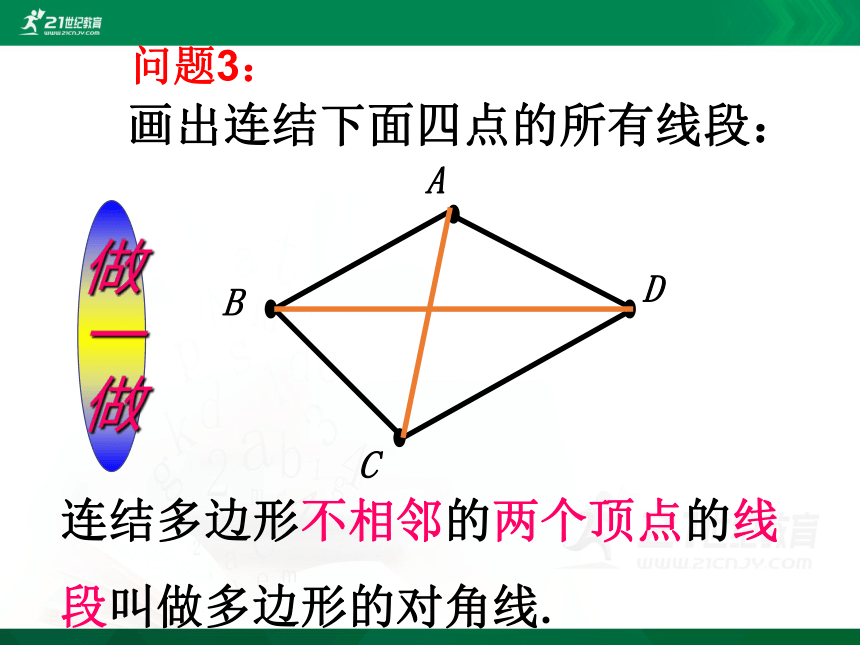
画出连结下面四点的所有线段:
连结多边形不相邻的两个顶点的线段叫做多边形的对角线.
做
一
做
A
B
C
D
问题3:
四边形的内角和
A
D
C
B
问题4:
四边形的内角和
A
D
C
B
结论:四边形的内角和为360o.
∠A+∠B+∠C+∠D=360o.
5边形
6边形
7边形
探究:多边形的内角和
对角线条数:
三角形个数:
内角和:
2
3
4
3
4
5
540°
720°
900°
…
n边形
?
?
?
问题5:
过多边形的一个顶点做对角线
n边形的内角和公式:
(n-2)×180°.
结论:
解: ∠ B与∠D互补.
在四边形ABCD 中,
∠A+∠B+∠C+∠D=(4-2) × 180 ° =360 °.
由∠A+∠C=180 ° ,得
∠B+∠D=360 °-(∠A+∠C )=360 °-180 °=180 °
即∠B与∠D互补.
例3 如图7-35,在四边形ABCD中,∠A与∠C互补.∠B与∠D有怎样的数量关系?为什么?
应用新知
考考你
1.如图所示的模板,按规定,AB,CD的延长线相交成80°的角,因交点不在板上,不便测量,质检员测得∠BAE=122°,∠DCF=155°.如果你是质检员,如何知道模板是否合格?为什么?
多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.
如:
如:
在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和.
结论:
?1,?2,?3,?4,?5的和等于360°.
A
B
C
D
E
1
2
3
4
5
7
8
9
10
11
想一想:
如果广场的形状是六边形、八边形,那么还有类似的结论吗?
如果广场的形状是六边形、八边形.它们的外角和也等于360°吗?
想一想:
还有什么方法可以推导出多边形外角和?
任何多边形的外角和都等于360°.
已知一个多边形,它的内角和与外角和相等,这个多边形是几边形?
解:设多边形的边数为n,那么它的内角和等于(n-2)×180°,外角和等于360°.由题意,得
(n-2) ×180°=360°.
解这个方程,得
n=4.
所以,这个多边形是四边形.
一个多边形的每个外角都是72°,这个多边形是几边形?
解:设多边形的变数是n,根据题意,得
n?72°=360°.
解得:n=5.
因此,这个多边形是五边形.
一个多边形的内角和等于它的外角和的5倍,这个多边形是几边形?
解:设这个多边形是n边形,根据题意,得
(n-2)?180°=5×360°.
解得:n=12.
因此,这个多边形是十二边形.
若一个多边形的每一个外角都等于24°,则这个多边形的边数是_____.
若一个多边形的每一个外角都等于30°,则它的内角和等于________.
各角都相等的五边形的每一个外角都等于_______.
如果一个多边形内角和对于外角和的二分之一倍,那么这个多边形的边数是__________.
1.一个多边形的外角都等于60°,这个多边形是几边形?
2.下图是三个完全相同的正多边形拼成的无缝隙、不重叠的图形的一部分,这种多边形是几边形?为什么?
3.直角三角形的两锐角之和是多少度?证明你的结论.
证明:
在△ABC中,
∵∠A+∠B+∠C=180°(三角形内角和定理),
∠C= 90°(已知),
∴∠A+∠B+90°=180° (等量代换) ,
∴∠A+∠B=180°-90°= 90° (等式性质).
即直角三角形的两锐角之和是90°.
A
B
C
证明:
在△ABC中,
∵∠A+∠B+∠C=180°(三角形内角和定理),
∠A=∠B=∠C (已知),
∴3∠A=180°(等量代换) ,
∴∠A=∠B=∠C =60°.
即正三角形的一个内角是60°.
4.正三角形的一个内角是多少度?证明你的结论.
A
B
C
5.一个多边形的内角和等是外角和的2倍,它是几边形?如果这个多边形的每个内角都相等,那么每个内角等于多少度?
解:设这个多边形是n边形,则它的内角和是(n-2)?180°,外角和等于360°,所以:
(n-2)?180°=2×360°.
解得:n=6.
这个多边形是六边形.
每个内角等于720°÷6=120°.
6.一个多边形能否有四个锐角?为什么?
解:不能.因为有四个锐角后其将会有4个钝角外角,那么外角和就会大于360°,所以不能有4个锐角内角.
矩形拼图
三角形拼图
六边形拼图
拼图游戏
谢谢聆听
7.5 多边形的内角和和外角和
第7章 平面图形的认识(二)
2020-2021学年度苏科版七年级下册
在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结.可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?” 老二很纳闷.
同学们,你们知道其中的道理吗?
内角三兄弟之争
新课导入
三角形三个内角的和等于
已知:△ABC.
求证:∠A +∠B +∠C=180°
180°
命题的正确性还要严密的推理证明
想一想:如何证明呢?
三角形内角和定理:
2
1
E
D
C
B
A
则 CE∥BA
(同位角相等,两直线平行).
∴ ∠1=∠A
(两直线平行,内错角相等).
∵B,C,D在同一直线上
∴ ∠1+∠2+∠ACB
=∠A+∠B+∠ACB
=180°
延长BC到D,在△ABC的外部,以CA为一边,
CE为另一边作∠2 =∠B,
例1 在△ABC中,∠A=40 ° ,∠B=∠C.求∠C的度数.
解:在△ABC,
由∠A+∠B+∠C=180 ° ,∠A=40 ° ,得
∠B+∠ C=180 °-∠A=180 ° -40 ° =140 °.
由∠ B=∠C,得
2∠C=140 ° ,∠C=70 °.
例2 如图7-30,△ABC的角平分线BD、CE相交于点P.∠A=70°.求∠BPC的度数.
解:在△ABC中,
由∠A+∠ABC+∠ACB=180 ° ,∠A=70 °,得
∠ABC+∠ACB=180 °-∠A=180 ° -70 ° =110 ° .
因为BD、CE分别平分∠ABC、∠ACB,
所以∠1= ∠ABC, ∠2= ∠ACB,
∠1+∠2= (∠ABC+ ∠ACB )= ×110 °=55 °.
在△PBC中,
由∠BPC+∠1+∠2=180 ° ,∠1+∠2=55 ° ,得
∠BPC=180 ° -(∠1+∠2)=180 °-55 ° =125 °.
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
为了证明三个角的和为1800,可以转化为一个平角,这种转化思想是数学中的常用方法.
比
一
比
?
1、你能说出什么叫四边形、五边形、多边形吗?
由n条不在同一直线上的线段首尾顺次连结组成的平面图形,称为n边形.
又称为多边形.
问题1:
你能说一说下面所指的是多边形的什么?
猜一猜
边
内角
顶点
问题2:
我们现在研究的是如图所示的多边形,是凸多边形;如图所示的多边形,是凹多边形,但不在现在研究的范围中.今后如果不说明,我们讲的多边形都是凸多边形.
比
一
比
请大家细心地填一填,多边形的内角,边,外角三者的关系表,你能发现什么规律?
3
3
4
4
5
5
6
6
7
7
n
n
6
8
10
12
14
2n
画出连结下面四点的所有线段:
连结多边形不相邻的两个顶点的线段叫做多边形的对角线.
做
一
做
A
B
C
D
问题3:
四边形的内角和
A
D
C
B
问题4:
四边形的内角和
A
D
C
B
结论:四边形的内角和为360o.
∠A+∠B+∠C+∠D=360o.
5边形
6边形
7边形
探究:多边形的内角和
对角线条数:
三角形个数:
内角和:
2
3
4
3
4
5
540°
720°
900°
…
n边形
?
?
?
问题5:
过多边形的一个顶点做对角线
n边形的内角和公式:
(n-2)×180°.
结论:
解: ∠ B与∠D互补.
在四边形ABCD 中,
∠A+∠B+∠C+∠D=(4-2) × 180 ° =360 °.
由∠A+∠C=180 ° ,得
∠B+∠D=360 °-(∠A+∠C )=360 °-180 °=180 °
即∠B与∠D互补.
例3 如图7-35,在四边形ABCD中,∠A与∠C互补.∠B与∠D有怎样的数量关系?为什么?
应用新知
考考你
1.如图所示的模板,按规定,AB,CD的延长线相交成80°的角,因交点不在板上,不便测量,质检员测得∠BAE=122°,∠DCF=155°.如果你是质检员,如何知道模板是否合格?为什么?
多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.
如:
如:
在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和.
结论:
?1,?2,?3,?4,?5的和等于360°.
A
B
C
D
E
1
2
3
4
5
7
8
9
10
11
想一想:
如果广场的形状是六边形、八边形,那么还有类似的结论吗?
如果广场的形状是六边形、八边形.它们的外角和也等于360°吗?
想一想:
还有什么方法可以推导出多边形外角和?
任何多边形的外角和都等于360°.
已知一个多边形,它的内角和与外角和相等,这个多边形是几边形?
解:设多边形的边数为n,那么它的内角和等于(n-2)×180°,外角和等于360°.由题意,得
(n-2) ×180°=360°.
解这个方程,得
n=4.
所以,这个多边形是四边形.
一个多边形的每个外角都是72°,这个多边形是几边形?
解:设多边形的变数是n,根据题意,得
n?72°=360°.
解得:n=5.
因此,这个多边形是五边形.
一个多边形的内角和等于它的外角和的5倍,这个多边形是几边形?
解:设这个多边形是n边形,根据题意,得
(n-2)?180°=5×360°.
解得:n=12.
因此,这个多边形是十二边形.
若一个多边形的每一个外角都等于24°,则这个多边形的边数是_____.
若一个多边形的每一个外角都等于30°,则它的内角和等于________.
各角都相等的五边形的每一个外角都等于_______.
如果一个多边形内角和对于外角和的二分之一倍,那么这个多边形的边数是__________.
1.一个多边形的外角都等于60°,这个多边形是几边形?
2.下图是三个完全相同的正多边形拼成的无缝隙、不重叠的图形的一部分,这种多边形是几边形?为什么?
3.直角三角形的两锐角之和是多少度?证明你的结论.
证明:
在△ABC中,
∵∠A+∠B+∠C=180°(三角形内角和定理),
∠C= 90°(已知),
∴∠A+∠B+90°=180° (等量代换) ,
∴∠A+∠B=180°-90°= 90° (等式性质).
即直角三角形的两锐角之和是90°.
A
B
C
证明:
在△ABC中,
∵∠A+∠B+∠C=180°(三角形内角和定理),
∠A=∠B=∠C (已知),
∴3∠A=180°(等量代换) ,
∴∠A=∠B=∠C =60°.
即正三角形的一个内角是60°.
4.正三角形的一个内角是多少度?证明你的结论.
A
B
C
5.一个多边形的内角和等是外角和的2倍,它是几边形?如果这个多边形的每个内角都相等,那么每个内角等于多少度?
解:设这个多边形是n边形,则它的内角和是(n-2)?180°,外角和等于360°,所以:
(n-2)?180°=2×360°.
解得:n=6.
这个多边形是六边形.
每个内角等于720°÷6=120°.
6.一个多边形能否有四个锐角?为什么?
解:不能.因为有四个锐角后其将会有4个钝角外角,那么外角和就会大于360°,所以不能有4个锐角内角.
矩形拼图
三角形拼图
六边形拼图
拼图游戏
谢谢聆听
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
