人教版八年级下册第十九章一次函数复习课件(17张)
文档属性
| 名称 | 人教版八年级下册第十九章一次函数复习课件(17张) |  | |
| 格式 | ppt | ||
| 文件大小 | 265.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-15 22:44:06 | ||
图片预览






文档简介
一次函数复习
回顾一:
1、形如________________的函数叫做一次函数.其中b=0时该
函数又叫做_______函数.
2、下列哪些函数是一次函数?
y=-3x; y= ; y=5x+2; y=4(x-3) -4x; y=x2+2; y=kx+5.
3、已知函数y=(m+2)x+3-m是一次函数,则m的取值范围
是_________,若此函数是正比例函数,则m的值是_______,
其解析式为_________.
y=kx+b(k≠0)
正比例
m≠-2
m=3
y=5x
小结一:
一次函数的定义.
y=kx+b(k≠0).
当b=0时是正比例函数
(是一次函数的特殊情况)
注意:
1、k≠0
2、等式右边是整式
3、自变量x的次数是一次
反馈一:
1、已知函数y=(2k-3)x+1-k是一次函数,则k的
取值范围是_________________________.
2、下列函数⑴y= ⑵y=2x-1 ⑶
⑷y=22-3x ⑸y= x2-1中,是一次函数的( )
A、4个 B、3个 C、2个 D、1个
C
回顾二:
1、一次函数y=kx+b(k≠0)的图像是 ( )
A、双曲线 B、直线 C、抛物线 D不能确定
2、一次函数y=-2x-4中,图像从左往右呈_____(上升、下
降)趋势,y随x的增大而_____, 图像与y轴交于点_______,图像与x轴交于点_______.
3、已知一次函数y=(1+2m)x-3中,函数值y随自变量x的增
大而增大,那么m的取值范围是____________.
4、如果直线y=k1x+b1与直线y=k2x+b2互相平行,那么( )
A、k1=k2 ,b1=b2 B、 k1≠k2 ,b1=b2
C、 k1=k2 , b1≠b2 D、 k1≠k2 ,b1≠b2
B
下降
减小
(0, -4)
(-2,0)
C
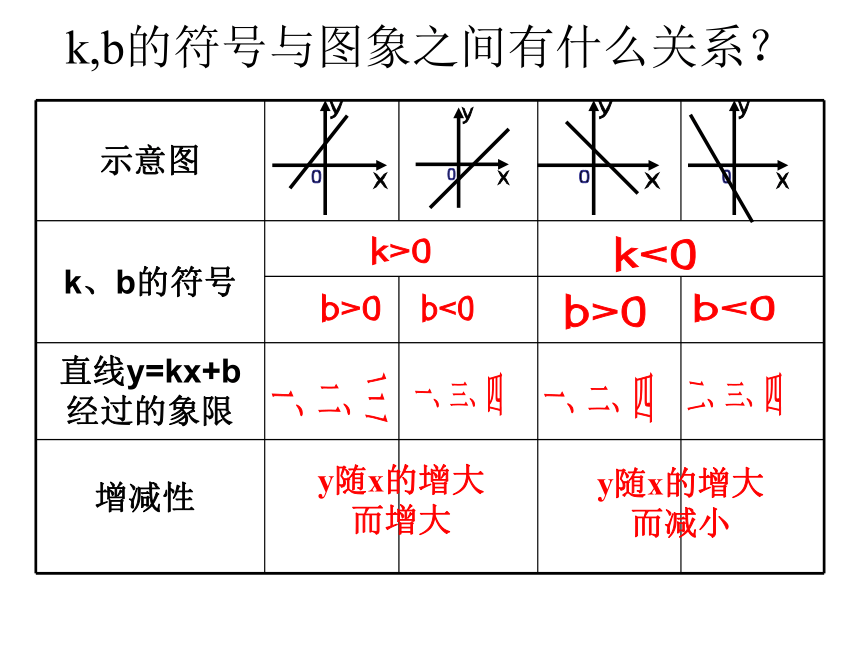
示意图
k、b的符号
直线y=kx+b经过的象限
x
y
0
x
y
0
x
y
0
x
y
0
k>0
b>0
一、二、三
b<0
一、三、四
k<0
b>0
一、二、四
b<0
二、三、四
k,b的符号与图象之间有什么关系?
增减性
y随x的增大
而增大
y随x的增大
而减小
小结二:
一次函数图像与性质:y=kx+b(k≠0)
1、图像是一条直线
2、当k>0时,图像从左往右呈上升趋势
当k<0时,图像从左往右呈下降趋势
3、b是直线与y轴交点的纵坐标
4、直线与x轴的交点的横坐标:令y=0,得x=
函数值y随自变量x的增大而增大
函数值y随自变量x的增大而减小
反馈二:
1、一次函数y=-1+ 中,图像从左往右呈______(上
升、下降)趋势,y随x的增大而______, 图像与y轴交于点_________.图像与x轴交于点_________.
2、直线y=kx+2与直线y= 平行,则k=_______.
3、已知一次函数y=(1-k)x+k,若k>1,则此函数的图像经过第____、____、____象限.
上升
增大
(0, -1)
( , 0)
一
二
四
4、已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐
标系内它的大致图象是( )
(A) (B) (C) (D)
A
5、一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的
高度h(厘米)与燃烧时间t(时)的函数关系式的图象是( )
0
t(时)
h(厘米)
4
20
t(时)
h(厘米)
4
20
0
t(时)
h(厘米)
4
20
0
t(时)
h(厘米)
4
20
0
(A) (B) (C) (D)
D
回顾三:
1、已知一次函数y=kx+3的图像经过点(2,5),求这个一次函数的解析式.
2、已知一次函数y=2x+b的图像经过点(-1,6),求这个一次函数的解析式为.
3、一次函数的图像经过点A(4,2)、B(5,1),求这个一次函数的解析式.
y=x+3
y=2x+8
y=-x+6
小结三:
一次函数解析式的确定
(待定系数法)
1、确定k、b,
设y=kx+b(k≠0)
(需要两个独立的条件)
2、把横坐标代入x,纵坐标代入y,列出方程组,求出k、b,再代回一次函数的解析式中
(2)直线与两坐标轴围成的面积;
一次函数y=ax+b经过点(1,2)、点(-1,6),求:
(1)这个一次函数的解析式;
讲一讲
(1)把点(1,2)和点(-1,6)代入
y=ax+b得:
∴一次函数的解析式:y=-2x+4
a=-2
b=4
2=a+ b
6=-a+b
{
解得
{
解:
(2)如图,直线y=-2x+4与y轴的交点A(0,4)与x轴的交点B(2,0)
∴OA=4,OB=2
∴S △AOB = OA × OB=4
1
2
x
y
0
B
A
M
P
x
y
0
B
A
讲一讲
一次函数y=ax+b经过点(1,2)、点(-1,6),求:
(1)这个一次函数的解析式;
(2)直线与两坐标轴围成的面积;
(3)如果正比例函数y= x与该一次函
数的交点P,求P点坐标和两直线与x轴围
成的三角形面积。
{
(3)由题意得
解得
{
∴P( ,1)
∴ OB=2 , PM=1
∴ S△OPB= OB×PM= ×2 ×1=1
1
2
1
2
小结:
1、一次函数的概念:函数y=_______(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。
kx +b
≠0
= 0
≠0
kx
★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,⑵、比例系数_____。
1
K≠0
2、正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________。
3、一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________。
0,0
1,k
一条直线
b
一条直线
4、正比例函数y=kx(k≠0)的性质:
⑴当k>0时,图象过______象限;y随x的增大而____。
⑵当k<0时,图象过______象限;y随x的增大而____。
一、三
增大
二、四
减小
5、一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图
中k、b的符号:
增大
减小
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
<
<
>
<
<
>
>
>
求直线y=2x+3、y=-2x-1及y轴围成的
三角形的面积
若将y轴改为x轴呢?
x
y
O
y=2x+3
y=-2x-1
A
B
C
D
P
作业
2、直线y1=kx与直线y2=kx-k在同一坐标系内的大致图象是( )
k>0
k<0
k<0
不平行
k>0 -k>0
k<0 -k<0
k<0 -k>0
(A)
(B)
(C)
(D)
C
做一做
回顾一:
1、形如________________的函数叫做一次函数.其中b=0时该
函数又叫做_______函数.
2、下列哪些函数是一次函数?
y=-3x; y= ; y=5x+2; y=4(x-3) -4x; y=x2+2; y=kx+5.
3、已知函数y=(m+2)x+3-m是一次函数,则m的取值范围
是_________,若此函数是正比例函数,则m的值是_______,
其解析式为_________.
y=kx+b(k≠0)
正比例
m≠-2
m=3
y=5x
小结一:
一次函数的定义.
y=kx+b(k≠0).
当b=0时是正比例函数
(是一次函数的特殊情况)
注意:
1、k≠0
2、等式右边是整式
3、自变量x的次数是一次
反馈一:
1、已知函数y=(2k-3)x+1-k是一次函数,则k的
取值范围是_________________________.
2、下列函数⑴y= ⑵y=2x-1 ⑶
⑷y=22-3x ⑸y= x2-1中,是一次函数的( )
A、4个 B、3个 C、2个 D、1个
C
回顾二:
1、一次函数y=kx+b(k≠0)的图像是 ( )
A、双曲线 B、直线 C、抛物线 D不能确定
2、一次函数y=-2x-4中,图像从左往右呈_____(上升、下
降)趋势,y随x的增大而_____, 图像与y轴交于点_______,图像与x轴交于点_______.
3、已知一次函数y=(1+2m)x-3中,函数值y随自变量x的增
大而增大,那么m的取值范围是____________.
4、如果直线y=k1x+b1与直线y=k2x+b2互相平行,那么( )
A、k1=k2 ,b1=b2 B、 k1≠k2 ,b1=b2
C、 k1=k2 , b1≠b2 D、 k1≠k2 ,b1≠b2
B
下降
减小
(0, -4)
(-2,0)
C
示意图
k、b的符号
直线y=kx+b经过的象限
x
y
0
x
y
0
x
y
0
x
y
0
k>0
b>0
一、二、三
b<0
一、三、四
k<0
b>0
一、二、四
b<0
二、三、四
k,b的符号与图象之间有什么关系?
增减性
y随x的增大
而增大
y随x的增大
而减小
小结二:
一次函数图像与性质:y=kx+b(k≠0)
1、图像是一条直线
2、当k>0时,图像从左往右呈上升趋势
当k<0时,图像从左往右呈下降趋势
3、b是直线与y轴交点的纵坐标
4、直线与x轴的交点的横坐标:令y=0,得x=
函数值y随自变量x的增大而增大
函数值y随自变量x的增大而减小
反馈二:
1、一次函数y=-1+ 中,图像从左往右呈______(上
升、下降)趋势,y随x的增大而______, 图像与y轴交于点_________.图像与x轴交于点_________.
2、直线y=kx+2与直线y= 平行,则k=_______.
3、已知一次函数y=(1-k)x+k,若k>1,则此函数的图像经过第____、____、____象限.
上升
增大
(0, -1)
( , 0)
一
二
四
4、已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐
标系内它的大致图象是( )
(A) (B) (C) (D)
A
5、一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的
高度h(厘米)与燃烧时间t(时)的函数关系式的图象是( )
0
t(时)
h(厘米)
4
20
t(时)
h(厘米)
4
20
0
t(时)
h(厘米)
4
20
0
t(时)
h(厘米)
4
20
0
(A) (B) (C) (D)
D
回顾三:
1、已知一次函数y=kx+3的图像经过点(2,5),求这个一次函数的解析式.
2、已知一次函数y=2x+b的图像经过点(-1,6),求这个一次函数的解析式为.
3、一次函数的图像经过点A(4,2)、B(5,1),求这个一次函数的解析式.
y=x+3
y=2x+8
y=-x+6
小结三:
一次函数解析式的确定
(待定系数法)
1、确定k、b,
设y=kx+b(k≠0)
(需要两个独立的条件)
2、把横坐标代入x,纵坐标代入y,列出方程组,求出k、b,再代回一次函数的解析式中
(2)直线与两坐标轴围成的面积;
一次函数y=ax+b经过点(1,2)、点(-1,6),求:
(1)这个一次函数的解析式;
讲一讲
(1)把点(1,2)和点(-1,6)代入
y=ax+b得:
∴一次函数的解析式:y=-2x+4
a=-2
b=4
2=a+ b
6=-a+b
{
解得
{
解:
(2)如图,直线y=-2x+4与y轴的交点A(0,4)与x轴的交点B(2,0)
∴OA=4,OB=2
∴S △AOB = OA × OB=4
1
2
x
y
0
B
A
M
P
x
y
0
B
A
讲一讲
一次函数y=ax+b经过点(1,2)、点(-1,6),求:
(1)这个一次函数的解析式;
(2)直线与两坐标轴围成的面积;
(3)如果正比例函数y= x与该一次函
数的交点P,求P点坐标和两直线与x轴围
成的三角形面积。
{
(3)由题意得
解得
{
∴P( ,1)
∴ OB=2 , PM=1
∴ S△OPB= OB×PM= ×2 ×1=1
1
2
1
2
小结:
1、一次函数的概念:函数y=_______(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。
kx +b
≠0
= 0
≠0
kx
★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,⑵、比例系数_____。
1
K≠0
2、正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________。
3、一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________。
0,0
1,k
一条直线
b
一条直线
4、正比例函数y=kx(k≠0)的性质:
⑴当k>0时,图象过______象限;y随x的增大而____。
⑵当k<0时,图象过______象限;y随x的增大而____。
一、三
增大
二、四
减小
5、一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图
中k、b的符号:
增大
减小
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
<
<
>
<
<
>
>
>
求直线y=2x+3、y=-2x-1及y轴围成的
三角形的面积
若将y轴改为x轴呢?
x
y
O
y=2x+3
y=-2x-1
A
B
C
D
P
作业
2、直线y1=kx与直线y2=kx-k在同一坐标系内的大致图象是( )
k>0
k<0
k<0
不平行
k>0 -k>0
k<0 -k<0
k<0 -k>0
(A)
(B)
(C)
(D)
C
做一做
