四川省凉山州2020-2021学年高一上学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 四川省凉山州2020-2021学年高一上学期期末考试数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 684.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 13:26:58 | ||
图片预览


文档简介
凉山州2020—2021学年度上期期末检测
高一数学试题
注意事项:全卷共8页(试题卷4页,答题卷4页),考试时间为120分钟,满分150分;请将自己的学校、姓名、考号写在答题卷密封线内,答题只能答在答题卷上,答题时用蓝黑墨水笔(芯)书写。考试结束后,只将答题卷交回。
第Ⅰ卷(选择题 共60分)
一、选择题(每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合,,则( )
A. B. C. D.
2.已知,且是第四象限的角,则( )
A. B. C. D.
3.下列函数中,在其定义域上既是奇函数又是单调递增函数的是( )
A. B. C. D.
4.已知函数,则( )
A.3 B.6 C.15 D.12
5.彝族图案作为人类社会发展的一种物质文化,有着灿烂历史。按照图案的载体大致分为彝族服饰图案,彝族漆器图案,彝族银器图案等。其中蕴含着丰富的数学文化,如图1:漆器图案中出现的“阿基米德螺线”,该曲线是由一动点沿一条射线以等角速度转动所形成的轨迹。这些螺线均匀分布,将其简化抽象为图2所示,若长为2个单位,则所对应的弧长为( )
图1 图2
A. B. C. D.
6.已知,,,则( )
A. B. C. D.
7.下列关于函数的零点所在区间最准确的是( )
A. B. C. D.
8.已知幂函数,满足在为减函数,则的值为( )
A.3或 B.3 C. D.
9.设角的终边过点,则等于( )
A. B.1 C. D.
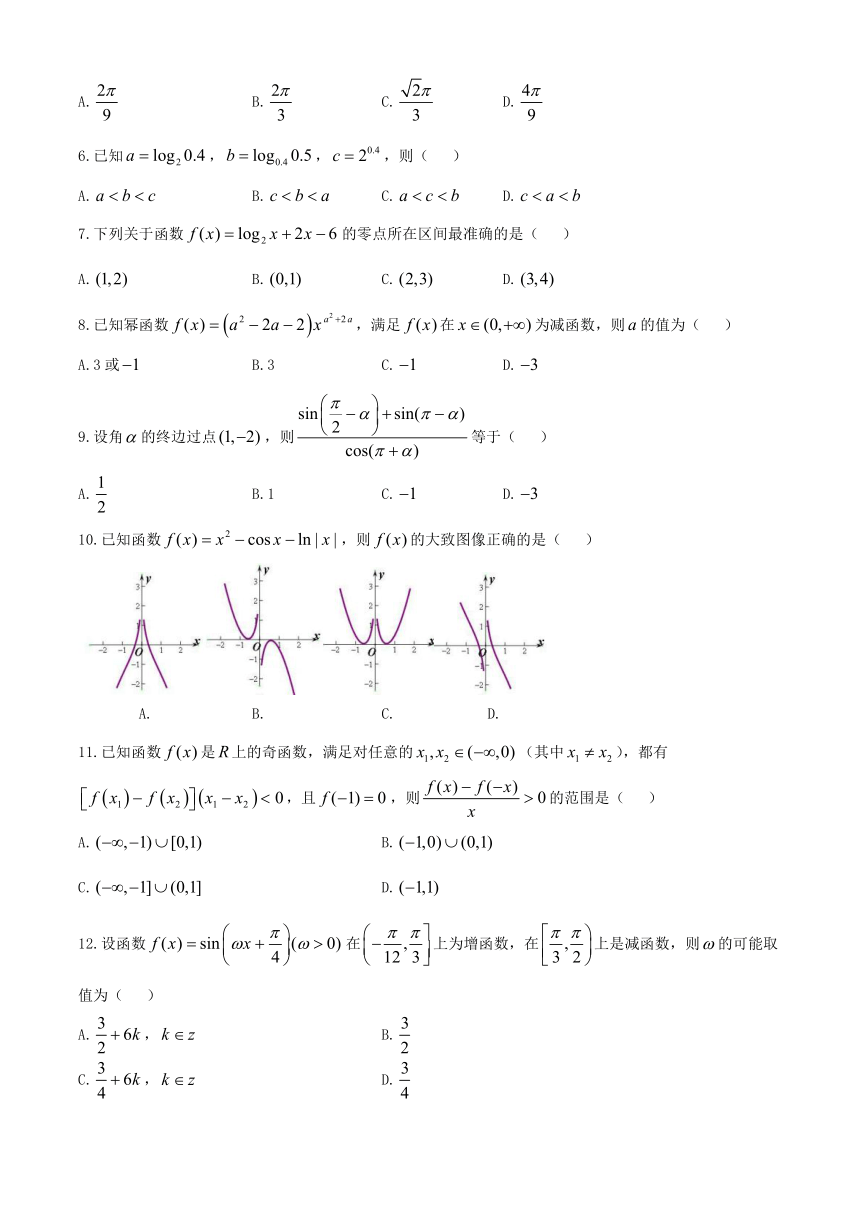
10.已知函数,则的大致图像正确的是( )
A. B. C. D.
11.已知函数是上的奇函数,满足对任意的(其中),都有,且,则的范围是( )
A. B.
C. D.
12.设函数在上为增函数,在上是减函数,则的可能取值为( )
A., B.
C., D.
第Ⅱ卷(非选择题 共90分)
二、填空题(共4个小题,每小题5分,共计20分,将答案填写在答题卡对应的横线上)
13.函数的定义域为 .
14.若,则 .
15.若函数在上是增函数,则的取值范围是 .
16.关于,有如下四个结论:
①是奇函数.
②图像关于轴对称.
③是的一条对称轴.
④有最大值和最小值.
其中说法正确的序号是 .
三、解答题(共6个小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.化简求值:
(1)
(2)已知,求
18.集合,.
(1)当时,求;
(2)若,求实数的取值范围.
19.已知函数是定义在上的偶函数,当时,.
(1)求在上的解析式;
(2)用定义法证明在上的单调性.
20.为助力凉山脱贫攻坚,州农科所通过培育新品种、引进新技术及配套高产栽培技术示范,为某县水果产业发展提供技术服务。研究发现,一亩脐橙树的产量(单位:吨)与肥料费用(单位:千元)近似满足如下关系:使用肥料不超过3千元时,若使用肥料超过3千元且不超过6千元时.此外,还需投入其他成本千元.若该脐橙的市场售价为1万元/吨,且市场上对脐橙的需求始终供不应求,该脐橙树每亩可获得的利润为.
(1)求的解析式;
(2)求当每亩地投入多少肥料时利润最大?并求出利润的最大值.
21.已知函数是定义在上的奇函数.
(1)求的值;
(2)对任意的,都有恒成立,求的取值范围.
22.已知函数的部分图像如图所示.
(1)求出函数的函数解析式;
(2)求函数的单调递增区间;
(3)求函数在上的最值.
凉山州2020—2021学年度上期期末检测
高一数学参答
一、选择题
1-5:DABCD 6-10:ACCBC 11、12:BD
二、填空题
13. 14. 15. 16.①③
三、解答题
17.解:(1)原式
(2)由得:,即.
18.解:(1)当时,,
由,可知:,
.
(2)由(1)知,,,且,
i)当时,,即;
ii)当时,,且满足,即.
综上所诉:的取值范围为:
19.解:(1)设,则,有
由于是定义在上的偶函数,即
故:,
(2)证明:设对任意的,且满足,有
,
,
故:函数在上为增函数.
20.解:(1)由题意可知:
即
(2)由(1)知:
①当时,为减函数,最大值为17千元.
②当时,,
时取得最大值为30千元.
综上所述:每亩地投入肥料5千元时,利润最大为30千元.
21.解:(1)由题意知:是定义在上的奇函数,
,
即
故:,
(2)由(1)知
因此在上是增函数,
对任意的,恒成立,
可转化,
根据在上是奇函数可知恒成立.
恒成立,
恒成立,
,
故:的取值范围为:.
22.解:(1)由图可知:,,即,
根据得:,
由得:,
,,
故:函数的解析式为:.
(2)由(1)知函数的解析式为,
,,
,,
故:函数的单调递增区间为,
(3)由(2)知在上为增函数,在上为减函数,
在时,取得最小值,
在时,取得最大值,
综上所述:在上的最小值为,最大值为2.
高一数学试题
注意事项:全卷共8页(试题卷4页,答题卷4页),考试时间为120分钟,满分150分;请将自己的学校、姓名、考号写在答题卷密封线内,答题只能答在答题卷上,答题时用蓝黑墨水笔(芯)书写。考试结束后,只将答题卷交回。
第Ⅰ卷(选择题 共60分)
一、选择题(每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合,,则( )
A. B. C. D.
2.已知,且是第四象限的角,则( )
A. B. C. D.
3.下列函数中,在其定义域上既是奇函数又是单调递增函数的是( )
A. B. C. D.
4.已知函数,则( )
A.3 B.6 C.15 D.12
5.彝族图案作为人类社会发展的一种物质文化,有着灿烂历史。按照图案的载体大致分为彝族服饰图案,彝族漆器图案,彝族银器图案等。其中蕴含着丰富的数学文化,如图1:漆器图案中出现的“阿基米德螺线”,该曲线是由一动点沿一条射线以等角速度转动所形成的轨迹。这些螺线均匀分布,将其简化抽象为图2所示,若长为2个单位,则所对应的弧长为( )
图1 图2
A. B. C. D.
6.已知,,,则( )
A. B. C. D.
7.下列关于函数的零点所在区间最准确的是( )
A. B. C. D.
8.已知幂函数,满足在为减函数,则的值为( )
A.3或 B.3 C. D.
9.设角的终边过点,则等于( )
A. B.1 C. D.
10.已知函数,则的大致图像正确的是( )
A. B. C. D.
11.已知函数是上的奇函数,满足对任意的(其中),都有,且,则的范围是( )
A. B.
C. D.
12.设函数在上为增函数,在上是减函数,则的可能取值为( )
A., B.
C., D.
第Ⅱ卷(非选择题 共90分)
二、填空题(共4个小题,每小题5分,共计20分,将答案填写在答题卡对应的横线上)
13.函数的定义域为 .
14.若,则 .
15.若函数在上是增函数,则的取值范围是 .
16.关于,有如下四个结论:
①是奇函数.
②图像关于轴对称.
③是的一条对称轴.
④有最大值和最小值.
其中说法正确的序号是 .
三、解答题(共6个小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.化简求值:
(1)
(2)已知,求
18.集合,.
(1)当时,求;
(2)若,求实数的取值范围.
19.已知函数是定义在上的偶函数,当时,.
(1)求在上的解析式;
(2)用定义法证明在上的单调性.
20.为助力凉山脱贫攻坚,州农科所通过培育新品种、引进新技术及配套高产栽培技术示范,为某县水果产业发展提供技术服务。研究发现,一亩脐橙树的产量(单位:吨)与肥料费用(单位:千元)近似满足如下关系:使用肥料不超过3千元时,若使用肥料超过3千元且不超过6千元时.此外,还需投入其他成本千元.若该脐橙的市场售价为1万元/吨,且市场上对脐橙的需求始终供不应求,该脐橙树每亩可获得的利润为.
(1)求的解析式;
(2)求当每亩地投入多少肥料时利润最大?并求出利润的最大值.
21.已知函数是定义在上的奇函数.
(1)求的值;
(2)对任意的,都有恒成立,求的取值范围.
22.已知函数的部分图像如图所示.
(1)求出函数的函数解析式;
(2)求函数的单调递增区间;
(3)求函数在上的最值.
凉山州2020—2021学年度上期期末检测
高一数学参答
一、选择题
1-5:DABCD 6-10:ACCBC 11、12:BD
二、填空题
13. 14. 15. 16.①③
三、解答题
17.解:(1)原式
(2)由得:,即.
18.解:(1)当时,,
由,可知:,
.
(2)由(1)知,,,且,
i)当时,,即;
ii)当时,,且满足,即.
综上所诉:的取值范围为:
19.解:(1)设,则,有
由于是定义在上的偶函数,即
故:,
(2)证明:设对任意的,且满足,有
,
,
故:函数在上为增函数.
20.解:(1)由题意可知:
即
(2)由(1)知:
①当时,为减函数,最大值为17千元.
②当时,,
时取得最大值为30千元.
综上所述:每亩地投入肥料5千元时,利润最大为30千元.
21.解:(1)由题意知:是定义在上的奇函数,
,
即
故:,
(2)由(1)知
因此在上是增函数,
对任意的,恒成立,
可转化,
根据在上是奇函数可知恒成立.
恒成立,
恒成立,
,
故:的取值范围为:.
22.解:(1)由图可知:,,即,
根据得:,
由得:,
,,
故:函数的解析式为:.
(2)由(1)知函数的解析式为,
,,
,,
故:函数的单调递增区间为,
(3)由(2)知在上为增函数,在上为减函数,
在时,取得最小值,
在时,取得最大值,
综上所述:在上的最小值为,最大值为2.
同课章节目录
