六年级数学下册 一课一练《正比例和反比例》习题1 -苏教版(含答案)
文档属性
| 名称 | 六年级数学下册 一课一练《正比例和反比例》习题1 -苏教版(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 571.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 21:19:05 | ||
图片预览


文档简介
《正比例和反比例》习题1
1、判断下面的两个量成正比例、反比例还是不成比例.
①圆的周长和半径.
②圆的面积和半径.
③正方形的周长和边长.
④圆柱的侧面积一定,圆柱的高和底面的半径.
⑤一个自然数和它的倒数.
⑥比例尺一定,图上距离和实际距离.
.
2、甲、乙是两个相关联的量,,和,,,,均不为是两组相对应的值,如下表.
甲
乙
(1)如果甲、乙成正比例,那么
.
(2)如果甲、乙成反比例,那么
.
3、、、三个相关联的量,并有.
(1)当一定时,与成 比例关系.
(2)当一定时,与成
比例关系.
(3)当一定时,与成
比例关系.
4、判断下面各题中的两个量,哪些成正比例?哪些成反比例,哪些不成比例?填入横线内.
(1)正方形的周长与边长.
(2)小丽步行上学的平均速度与所花时间.
(3)一个人的身高和年龄.
(4)三角形的面积一定,它的底和高.
(5)一捆100米长的电线,用去的长度和剩下的长度.
.
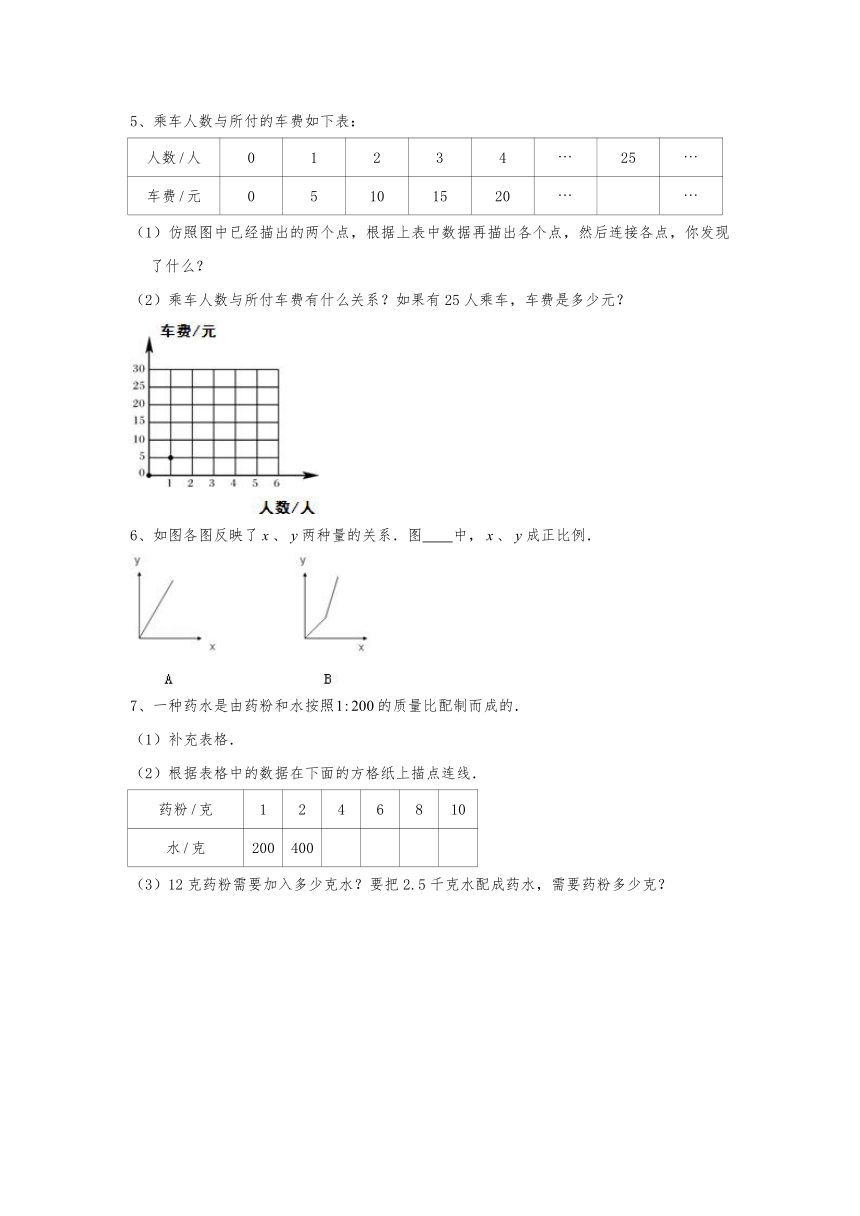
5、乘车人数与所付的车费如下表:
人数人
0
1
2
3
4
25
车费元
0
5
10
15
20
(1)仿照图中已经描出的两个点,根据上表中数据再描出各个点,然后连接各点,你发现了什么?
(2)乘车人数与所付车费有什么关系?如果有25人乘车,车费是多少元?
6、如图各图反映了、两种量的关系.图 中,、成正比例.
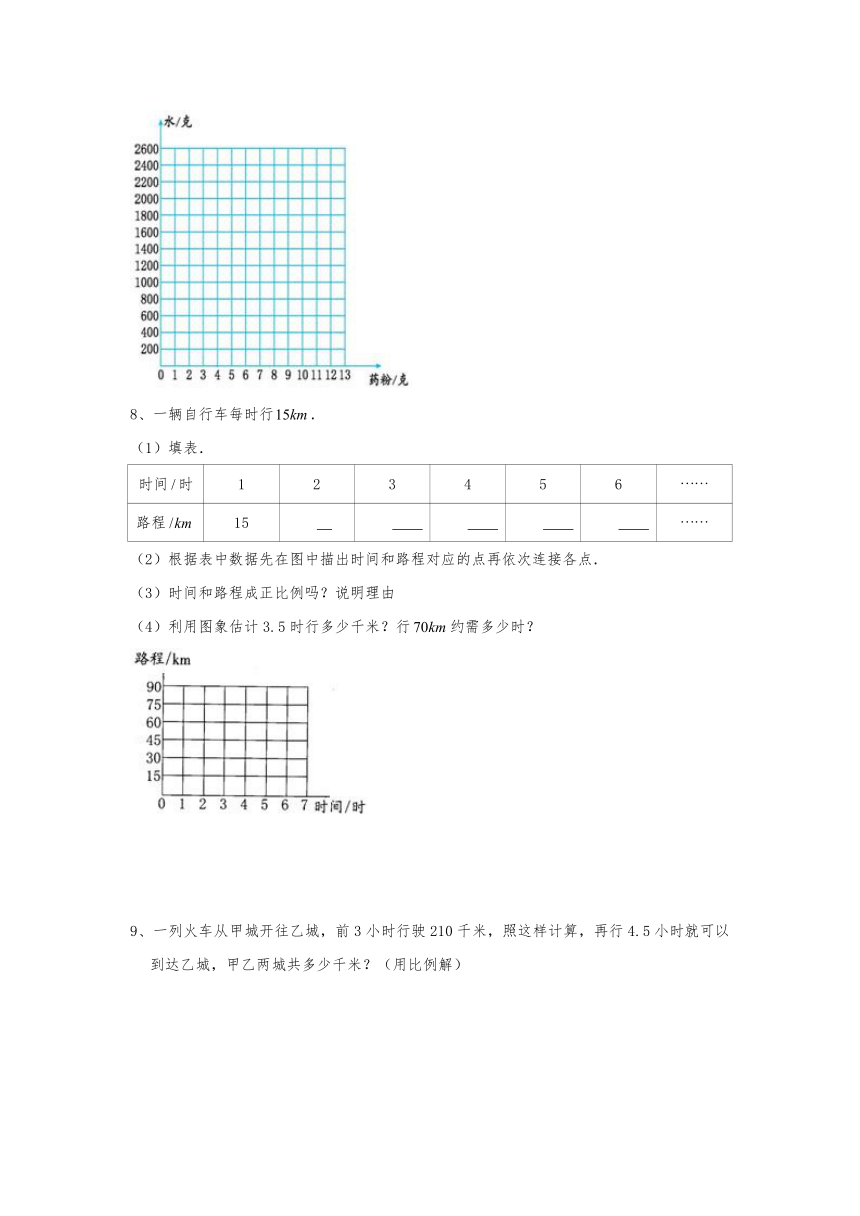
7、一种药水是由药粉和水按照的质量比配制而成的.
(1)补充表格.
(2)根据表格中的数据在下面的方格纸上描点连线.
药粉克
1
2
4
6
8
10
水克
200
400
(3)12克药粉需要加入多少克水?要把2.5千克水配成药水,需要药粉多少克?
8、一辆自行车每时行.
(1)填表.
时间时
1
2
3
4
5
6
路程
15
(2)根据表中数据先在图中描出时间和路程对应的点再依次连接各点.
(3)时间和路程成正比例吗?说明理由
(4)利用图象估计3.5时行多少千米?行约需多少时?
9、一列火车从甲城开往乙城,前3小时行驶210千米,照这样计算,再行4.5小时就可以到达乙城,甲乙两城共多少千米?(用比例解)
10、在比例尺是地图上,量得北京到杭州的铁路长4.7厘米,这条铁路实际长多少千米?(用两种方法)
11、法国巴黎的埃菲尔铁塔高.北京的“世界公园”里有一座埃菲尔铁塔的模型,它的高度与原塔高度的比是.这座模型高多少米?(用比例解)
12、某工程队要铺设一条公路,前20天已铺设了2.8千米,照这样计算,剩下的4.2千米,还要多少天才能铺完?(用比例解)
13、铺地砖:
(1)小芳家的客厅是一个长方形,按原计划选用边长是4分米的方砖需250块.如果改用边长5分米的方砖来铺需多少块?(用比例解)
(2)从价格方面考虑,选用哪种地砖较合适?(边长4分米的每块12.8元,铺每平方米手工费13元;边长5分米的每块22元,铺每平方米手工费8元).
14、某工厂四月份天)计划生产一批零件,平均每天要生产400个才能完成任务,实际上前6天就生产了3000个.照这样计算,完成原计划任务要用多少天?(分别用正、反比例解)
15、某厂生产一批水泥,原计划每天生产150吨,20天可以完成任务.实际每天比原计划增产,实际可以少用几天?(用比例解)
16、刘师傅要加工一批零件,每小时加工40个,3小时可以完成,如果要提1小时完成任务,工作效率需提高百分之几?(用比例的方法解)
答案
1、解:由思路分析知:
①圆的周长和半径.成正比例关系;
②圆的面积和半径.不成比例关系;
③正方形的周长和边长.成正比例关系;
④圆柱的侧面积一定,圆柱的高和底面的半径.成反比例关系;
⑤一个自然数和它的倒数.成反比例关系;
⑥比例尺一定,图上距离和实际距离.成正比例关系.
故答案为:成正比例关系;不成比例关系;成正比例关系;成反比例关系;成反比例关系;成正比例关系.
2、解:(1)如果甲、乙成正比例,那么,即;
(2)如果甲、乙成反比例,那么;
故答案为:、、、,、、、.
3、解:、、三个相关联的量,并有.
(1)当一定时,与成
反比例关系.
(2)当一定时,与成
正比例关系.
(3)当一定时,与成
正比例关系.
故答案为:反,正,正.
4、解:
(1)因为正方形的周长边长,所以正方形的周长边长(一定),即正方形的周长和它的边长的比值一定,符合正比例的意义,所以正方形的边长和周长成正比例;
(2)小丽每天步行上学的速度和时间是两种相关联的量,它们与小丽家到学校的距离有下面的关系:
速度时间家到学校的距离(一定);已知小丽到学校的距离一定,也就是小丽每天步行上学的速度和时间的乘积一定,符合反比例的意义,所以小丽每天步行上学的速度和时间成反比例.
(3)通常在生长期,人的身高是随着年龄的增长而增长,但是生长期过了后,骨膜会闭合,停止长高;
即人的身高与年龄的比值是不一定的,所以一个人的年龄与身高不成比例.
(4)三角形的底高面积(一定),是乘积一定,它的底和高成反比例.
(5)因为用的长度剩下的长度一捆电线的长度,所以用的长度与剩下的长度的比值和乘积都不一定,所以用的长度和剩下的长度不成比例.
故答案为:成正比例,成反比例,不成比例,成反比例,不成比例.
5、解:(1)如图:
(2)所付车费人数每人的车费(一定),乘车人数与所付车费成正比例;
(元
答:如果有25人乘车,车费是125元.
6、解:因为正比例的图形是一条直线,所以图中,、成正比例.
故答案为:.
7、解:(1)填表如下:
药粉克
1
2
4
6
8
10
水克
200
400
800
1200
1600
2000
(2)作图如下:
(3)(克,
2.5千克克,
(克,
答:12克药粉需要加水2400克,要把2.5千克水配成药水,需要药粉12.5克.
8、解:(1)(千米),(千米),(千米),(千米),(千米)
填表如下:
时间时
1
2
3
4
5
6
路程
15
30
45
60
75
90
(2)根据数据连线后如下图:
(3)时间和路程成正比例;因为自行车行驶的速度一定,也就是路程和时间的比值一定,所以时间和路程成正比例.
(4)图象是一条经过原点的直线,从图象中可看出自行车3.5小时约行52.5千米;行驶70千米用小时;
答:3.5小时行驶52.5千米.行驶70千米用小时.
故答案为:30;45;60;75;90.
9、解:设甲乙两城共千米.
;
答:甲乙两城共525千米.
10、解:方法一:
,
,
(厘米);
164500000厘米千米;
方法二:设这条铁路实际长厘米,则:
,
,
;
164500000厘米千米;
答:这条铁路实际长1645千米.
11、解:设这座模型高米,
则,
,
;
答:这座模型高32米.
12、解:设还要天才能铺完.
;
答:还要30天才能铺完.
13、解:(1)设用边长5分米的方砖来铺需块,
,
,
,
,
答:改用边长5分米的方砖来铺需160块.
(2)小芳家客厅的面积:(平方分米)平方米,
用边长是4分米的方砖花的钱数:(元,
手工费:(元,
总共花钱数:(元;
用边长5分米的方砖花的钱数:(元,
手工费:(元,
总共花钱数:(元,
,
所以选用边长是4分米的方砖较合适.
答:选用边长是4分米的方砖较合适.
14、解:(1)设完成原计划任务要用天.
;
(2)设完成原计划任务要用天.
;
答:完成原计划任务要用24天.
15、解:实际每天生产水泥的吨数:,
,
(吨,
设实际可以用天完成,
,
,
,
实际可以少用的天数:(天,
答:实际可以少用5天.
16、解:设提前1小时完成任务时的工作效率为个,
,
,
,
;
,
,
;
答:工作效率需提高.
1、判断下面的两个量成正比例、反比例还是不成比例.
①圆的周长和半径.
②圆的面积和半径.
③正方形的周长和边长.
④圆柱的侧面积一定,圆柱的高和底面的半径.
⑤一个自然数和它的倒数.
⑥比例尺一定,图上距离和实际距离.
.
2、甲、乙是两个相关联的量,,和,,,,均不为是两组相对应的值,如下表.
甲
乙
(1)如果甲、乙成正比例,那么
.
(2)如果甲、乙成反比例,那么
.
3、、、三个相关联的量,并有.
(1)当一定时,与成 比例关系.
(2)当一定时,与成
比例关系.
(3)当一定时,与成
比例关系.
4、判断下面各题中的两个量,哪些成正比例?哪些成反比例,哪些不成比例?填入横线内.
(1)正方形的周长与边长.
(2)小丽步行上学的平均速度与所花时间.
(3)一个人的身高和年龄.
(4)三角形的面积一定,它的底和高.
(5)一捆100米长的电线,用去的长度和剩下的长度.
.
5、乘车人数与所付的车费如下表:
人数人
0
1
2
3
4
25
车费元
0
5
10
15
20
(1)仿照图中已经描出的两个点,根据上表中数据再描出各个点,然后连接各点,你发现了什么?
(2)乘车人数与所付车费有什么关系?如果有25人乘车,车费是多少元?
6、如图各图反映了、两种量的关系.图 中,、成正比例.
7、一种药水是由药粉和水按照的质量比配制而成的.
(1)补充表格.
(2)根据表格中的数据在下面的方格纸上描点连线.
药粉克
1
2
4
6
8
10
水克
200
400
(3)12克药粉需要加入多少克水?要把2.5千克水配成药水,需要药粉多少克?
8、一辆自行车每时行.
(1)填表.
时间时
1
2
3
4
5
6
路程
15
(2)根据表中数据先在图中描出时间和路程对应的点再依次连接各点.
(3)时间和路程成正比例吗?说明理由
(4)利用图象估计3.5时行多少千米?行约需多少时?
9、一列火车从甲城开往乙城,前3小时行驶210千米,照这样计算,再行4.5小时就可以到达乙城,甲乙两城共多少千米?(用比例解)
10、在比例尺是地图上,量得北京到杭州的铁路长4.7厘米,这条铁路实际长多少千米?(用两种方法)
11、法国巴黎的埃菲尔铁塔高.北京的“世界公园”里有一座埃菲尔铁塔的模型,它的高度与原塔高度的比是.这座模型高多少米?(用比例解)
12、某工程队要铺设一条公路,前20天已铺设了2.8千米,照这样计算,剩下的4.2千米,还要多少天才能铺完?(用比例解)
13、铺地砖:
(1)小芳家的客厅是一个长方形,按原计划选用边长是4分米的方砖需250块.如果改用边长5分米的方砖来铺需多少块?(用比例解)
(2)从价格方面考虑,选用哪种地砖较合适?(边长4分米的每块12.8元,铺每平方米手工费13元;边长5分米的每块22元,铺每平方米手工费8元).
14、某工厂四月份天)计划生产一批零件,平均每天要生产400个才能完成任务,实际上前6天就生产了3000个.照这样计算,完成原计划任务要用多少天?(分别用正、反比例解)
15、某厂生产一批水泥,原计划每天生产150吨,20天可以完成任务.实际每天比原计划增产,实际可以少用几天?(用比例解)
16、刘师傅要加工一批零件,每小时加工40个,3小时可以完成,如果要提1小时完成任务,工作效率需提高百分之几?(用比例的方法解)
答案
1、解:由思路分析知:
①圆的周长和半径.成正比例关系;
②圆的面积和半径.不成比例关系;
③正方形的周长和边长.成正比例关系;
④圆柱的侧面积一定,圆柱的高和底面的半径.成反比例关系;
⑤一个自然数和它的倒数.成反比例关系;
⑥比例尺一定,图上距离和实际距离.成正比例关系.
故答案为:成正比例关系;不成比例关系;成正比例关系;成反比例关系;成反比例关系;成正比例关系.
2、解:(1)如果甲、乙成正比例,那么,即;
(2)如果甲、乙成反比例,那么;
故答案为:、、、,、、、.
3、解:、、三个相关联的量,并有.
(1)当一定时,与成
反比例关系.
(2)当一定时,与成
正比例关系.
(3)当一定时,与成
正比例关系.
故答案为:反,正,正.
4、解:
(1)因为正方形的周长边长,所以正方形的周长边长(一定),即正方形的周长和它的边长的比值一定,符合正比例的意义,所以正方形的边长和周长成正比例;
(2)小丽每天步行上学的速度和时间是两种相关联的量,它们与小丽家到学校的距离有下面的关系:
速度时间家到学校的距离(一定);已知小丽到学校的距离一定,也就是小丽每天步行上学的速度和时间的乘积一定,符合反比例的意义,所以小丽每天步行上学的速度和时间成反比例.
(3)通常在生长期,人的身高是随着年龄的增长而增长,但是生长期过了后,骨膜会闭合,停止长高;
即人的身高与年龄的比值是不一定的,所以一个人的年龄与身高不成比例.
(4)三角形的底高面积(一定),是乘积一定,它的底和高成反比例.
(5)因为用的长度剩下的长度一捆电线的长度,所以用的长度与剩下的长度的比值和乘积都不一定,所以用的长度和剩下的长度不成比例.
故答案为:成正比例,成反比例,不成比例,成反比例,不成比例.
5、解:(1)如图:
(2)所付车费人数每人的车费(一定),乘车人数与所付车费成正比例;
(元
答:如果有25人乘车,车费是125元.
6、解:因为正比例的图形是一条直线,所以图中,、成正比例.
故答案为:.
7、解:(1)填表如下:
药粉克
1
2
4
6
8
10
水克
200
400
800
1200
1600
2000
(2)作图如下:
(3)(克,
2.5千克克,
(克,
答:12克药粉需要加水2400克,要把2.5千克水配成药水,需要药粉12.5克.
8、解:(1)(千米),(千米),(千米),(千米),(千米)
填表如下:
时间时
1
2
3
4
5
6
路程
15
30
45
60
75
90
(2)根据数据连线后如下图:
(3)时间和路程成正比例;因为自行车行驶的速度一定,也就是路程和时间的比值一定,所以时间和路程成正比例.
(4)图象是一条经过原点的直线,从图象中可看出自行车3.5小时约行52.5千米;行驶70千米用小时;
答:3.5小时行驶52.5千米.行驶70千米用小时.
故答案为:30;45;60;75;90.
9、解:设甲乙两城共千米.
;
答:甲乙两城共525千米.
10、解:方法一:
,
,
(厘米);
164500000厘米千米;
方法二:设这条铁路实际长厘米,则:
,
,
;
164500000厘米千米;
答:这条铁路实际长1645千米.
11、解:设这座模型高米,
则,
,
;
答:这座模型高32米.
12、解:设还要天才能铺完.
;
答:还要30天才能铺完.
13、解:(1)设用边长5分米的方砖来铺需块,
,
,
,
,
答:改用边长5分米的方砖来铺需160块.
(2)小芳家客厅的面积:(平方分米)平方米,
用边长是4分米的方砖花的钱数:(元,
手工费:(元,
总共花钱数:(元;
用边长5分米的方砖花的钱数:(元,
手工费:(元,
总共花钱数:(元,
,
所以选用边长是4分米的方砖较合适.
答:选用边长是4分米的方砖较合适.
14、解:(1)设完成原计划任务要用天.
;
(2)设完成原计划任务要用天.
;
答:完成原计划任务要用24天.
15、解:实际每天生产水泥的吨数:,
,
(吨,
设实际可以用天完成,
,
,
,
实际可以少用的天数:(天,
答:实际可以少用5天.
16、解:设提前1小时完成任务时的工作效率为个,
,
,
,
;
,
,
;
答:工作效率需提高.
