六年级数学下册 一课一练《正比例和反比例》习题2 苏教版(含答案)
文档属性
| 名称 | 六年级数学下册 一课一练《正比例和反比例》习题2 苏教版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 614.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 00:00:00 | ||
图片预览




文档简介
《正比例和反比例》习题2
1、下面 中两种量成正比例关系,
中两种量成反比例关系.
.甲、乙两地相距120千米,汽车每小时所行路程和时间
.圆的周长和圆周率
.总钱数一定,花了的钱和剩余的钱
.正方体一个面的面积和它的表面积.
2、当路程一定时,速度与时间成 比例.
当比例尺一定时,图上距离与实际距离成
比例.
当煤的总吨数一定时,用去的吨数与剩下的吨数
比例.
3、如果,、均不为那么和成 比例;如果,那么和成
比例.
4、在式子中,如果一定,和成 比例;如果一定,那么和成
比例.
5、如果,和成 比例;如果,和成
比例
6、同一时间、同一地点测得树高和影长的数据如表:
树高
2
3
4
6
影长
1.6
2.4
3.2
4.8
(1)在图中描出表示树高和对应影长的点,然后把它们连起来.
(2)连线以后观察,它们是在一条直线上吗?
,说明树高和影长成
关系.
(3)不计算,利用图象判断,树高8米时,影长
米?影长4米时,树高
米?
7、如图的图象表示一幅地图的图上距离和实际距离的关系.
(1)图上距离和实际距离成
比例.
(2)这幅地图的比例尺是
.
(3)在这幅地图上量得两地的图上距离是12厘米,两地的实际距离是多少千米?
8、实践活动:旗杆有多高?
操场上,同学们正在阳光下测量竹竿、木棒的高度以及它们影子的长度,测量数据如下表:
实际高度
影长
实际高度与影长的比值
竹竿
1
2
0.5
竹竿
2
1.6
0.4
木棒
1
1
0.25
(1)计算并填写表格;
(2)仔细观察表格中竹竿、木棒的实际高度与影长的比值,你有什么发现?
(3)根据你的发现想一想,如果这时同学们测出旗杆的影长是
3.2
米,那么旗杆的实际高度应是
米.
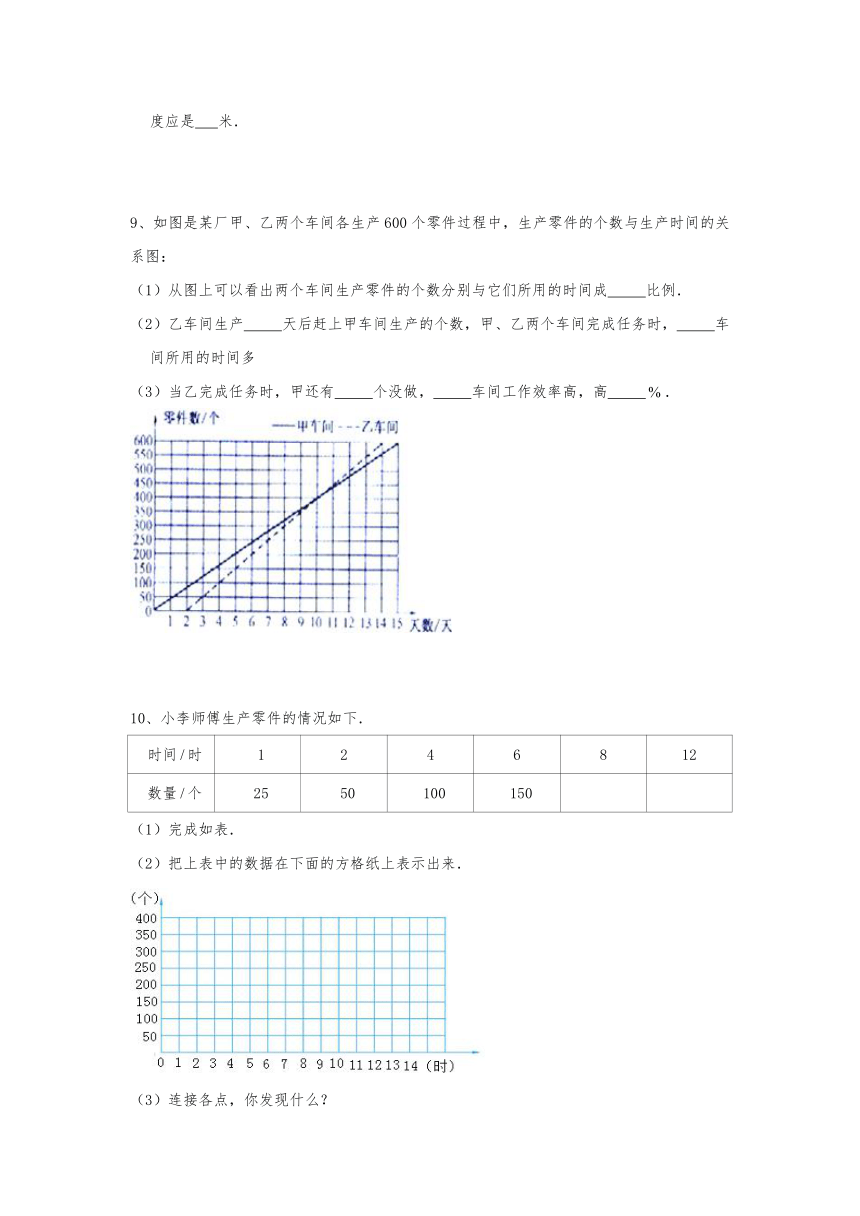
9、如图是某厂甲、乙两个车间各生产600个零件过程中,生产零件的个数与生产时间的关系图:
(1)从图上可以看出两个车间生产零件的个数分别与它们所用的时间成
比例.
(2)乙车间生产
天后赶上甲车间生产的个数,甲、乙两个车间完成任务时,
车间所用的时间多
(3)当乙完成任务时,甲还有
个没做,
车间工作效率高,高
.
10、小李师傅生产零件的情况如下.
时间时
1
2
4
6
8
12
数量个
25
50
100
150
(1)完成如表.
(2)把上表中的数据在下面的方格纸上表示出来.
(3)连接各点,你发现什么?
(4)表中的数量和时间有什么关系?
(5)估计一下,2.5小时大约做多少个零件?5.5小时呢?
11、在比例尺是的地图上,两地间的距离是16厘米.
(1)两地间的实际距离是多少千米?
(2)一列火车由到用了3小时,火车每小时行多少千米?
12、一个房间,用边长3分米的方砖铺地,需要432块,如果改用边长4分米的方砖铺地,需要多少块?
13、从儿童节那天开始,小明读名著《红楼梦》.开始的4天他读完了32页,照这样计算,这个月小明一共可以读完多少页?(用比例规范解答)
14、小兰的身高,她的影子长是.如果同一时间,同一地点测得一棵树的影子长,这棵树有多高?
15、某小区维修线路,需停电半小时,妈妈找来一根长20厘米的蜡烛,点燃8分钟后,还剩15厘米,请问,这根蜡烛够燃烧到送电吗?(用比例知识规范解答并简要说明理由)
16、某人步行4小时走了22.4千米,照这样的速度,如果再走3小时,一共可以走多少千米?(用比例解)
17、一批零件计划每天生产42套,20天完成,实际每天多生产14套,结果提前几天就完成了任务,(用比例解)
18、一个筑路队铺一条公路,原计划每天铺1.6千米,30天铺完,实际每天比原计划多铺0.8千米,实际多少天完成?(用比例解)
答案
1、解:、甲、乙
两地相距120千米,汽车每小时所行路程时间甲、乙
两地相距120千米(一定),所以成反比例;
、圆的周长圆周率圆的直径,由于圆周率是定值,所以不成比例;
、花了的剩余的钱总钱数(一定),是和一定,所以不成比例;
、正方体的表面积一个面的面积(一定),所以成正比例.
故答案为:,.
2、解:(1)速度时间路程(一定),是乘积一定
所以当路程一定时,速度与时间成反比例.
(2)图上距离:实际距离比例尺(一定),是比值一定
所以当比例尺一定时,图上距离与实际距离成正比例
(3)用去的吨数剩下的吨数煤的总吨数(一定),既不是乘积一定也不是比值一定.
所以当煤的总吨数一定时,用去的吨数与剩下的吨数不成比例.
故答案为:反,正,不成.
3、解:如果,、均不为,即,是比值一定,则和成正比例;
如果,即,是乘积一定,那么和成反比例.
故答案为:正,反.
4、解:因为子中,如果一定,
即比值一定,所以和成正比例;
因为
所以,所以如果一定,即乘积一定,所以和成反比例.
故答案为:正,反.
5、解:如果,则(一定),则和成
反比例;
如果,即(一定),所以和成
正比例
故答案为:反,正.
6、解:(1)所作图象如下图,观察发现:表示树高和对应影长的点,都在一条直线上.
(2)连线以后,发现表示树高和对应影长的点,都在一条直线上,这说明树高和影长成正比例关系,
因为随着树的高度的增加,影长也在增加,且树高与影长的商是一定的,所以树高和影长成正比例关系;
(3)设树高8时,影长为米,影长时,树高米,
则有
;
答:树高时,影长6.4米,影长时,树高5米.
故答案为:在、正比例;
6.4,5.
7、解:(1)2厘米:50千米
厘米:5000000厘米
4厘米:100千米
厘米:10000000厘米
因为比例尺(一定)
所以图上距离和实际距离成正比例.
(2)2厘米:50千米
厘米:5000000厘米
,
答:这幅地图的比例尺是.
(3)
(厘米),
30000000厘米千米,
答:两地的实际距离是300千米.
故答案为:正比例;.
8、解:(1)
,
,
,
填表如下:
实际高度
影长
实际高度与影长的比值
竹竿
1
2
0.5
4
竹竿
2
1.6
0.4
4
木棒
1
1
0.25
4
(2)仔细观察表格中竹竿、木棒的实际高度与影长的比值,,发现比值是比值一定,所以实际高度与影长之间成正比例;
(3)(米;
答:旗杆的实际高度应是12.8米,
故答案为:12.8.
9、解:(1)因为两种量是否是对应的比值一定
所以两个车间生产零件的个数分别与它们所用的时间成正比例.
(2)乙车间生产9天后赶上甲车间生产的个数,甲、乙两个车间完成任务时,甲车间所用的时间多.
(3)(个
(个
答:高.
故答案为:正,9,甲,50,乙,25.
10、解:(1)
时间时
1
2
4
6
8
12
数量个
25
50
100
150
200
300
(2)
(3)我发现加工零件的时间和数量成正比例关系.
(4)加工零件的时间和数量成正比例关系
(5)(个
(个
答:2.5小时大约做63个零件,5.5小时大约做138个零件.
11、解:(1)(厘米);
96000000厘米(千米);
(2)(千米);
答:两地间的实际距离是960千米,火车每小时行320千米.
12、解:设需要块.
;
答:需要243块.
13、解:设小明一个月天)可以页书,
,
,
,
;
答:这个月小明一共可以读完240页.
14、解:设这棵树的高为米,
,
,
,
.
答:这棵树有2.5米.
15、解:20厘米的蜡烛燃烧所用的时间为分钟,
,
,
,
,
,
因为半小时分钟,
,
所以这根蜡烛够燃烧到送电;
答:这根蜡烛够燃烧到送电.
16、解;设一共可以走千米,
,
,
,
,
.
答:一共可以走39.2千米.
17、解:设可以提前天完成.
,
,
;
答:可以提前5天完成.
18、解:设实际天完成,
则,
,
;
答:实际20天完成.
1、下面 中两种量成正比例关系,
中两种量成反比例关系.
.甲、乙两地相距120千米,汽车每小时所行路程和时间
.圆的周长和圆周率
.总钱数一定,花了的钱和剩余的钱
.正方体一个面的面积和它的表面积.
2、当路程一定时,速度与时间成 比例.
当比例尺一定时,图上距离与实际距离成
比例.
当煤的总吨数一定时,用去的吨数与剩下的吨数
比例.
3、如果,、均不为那么和成 比例;如果,那么和成
比例.
4、在式子中,如果一定,和成 比例;如果一定,那么和成
比例.
5、如果,和成 比例;如果,和成
比例
6、同一时间、同一地点测得树高和影长的数据如表:
树高
2
3
4
6
影长
1.6
2.4
3.2
4.8
(1)在图中描出表示树高和对应影长的点,然后把它们连起来.
(2)连线以后观察,它们是在一条直线上吗?
,说明树高和影长成
关系.
(3)不计算,利用图象判断,树高8米时,影长
米?影长4米时,树高
米?
7、如图的图象表示一幅地图的图上距离和实际距离的关系.
(1)图上距离和实际距离成
比例.
(2)这幅地图的比例尺是
.
(3)在这幅地图上量得两地的图上距离是12厘米,两地的实际距离是多少千米?
8、实践活动:旗杆有多高?
操场上,同学们正在阳光下测量竹竿、木棒的高度以及它们影子的长度,测量数据如下表:
实际高度
影长
实际高度与影长的比值
竹竿
1
2
0.5
竹竿
2
1.6
0.4
木棒
1
1
0.25
(1)计算并填写表格;
(2)仔细观察表格中竹竿、木棒的实际高度与影长的比值,你有什么发现?
(3)根据你的发现想一想,如果这时同学们测出旗杆的影长是
3.2
米,那么旗杆的实际高度应是
米.
9、如图是某厂甲、乙两个车间各生产600个零件过程中,生产零件的个数与生产时间的关系图:
(1)从图上可以看出两个车间生产零件的个数分别与它们所用的时间成
比例.
(2)乙车间生产
天后赶上甲车间生产的个数,甲、乙两个车间完成任务时,
车间所用的时间多
(3)当乙完成任务时,甲还有
个没做,
车间工作效率高,高
.
10、小李师傅生产零件的情况如下.
时间时
1
2
4
6
8
12
数量个
25
50
100
150
(1)完成如表.
(2)把上表中的数据在下面的方格纸上表示出来.
(3)连接各点,你发现什么?
(4)表中的数量和时间有什么关系?
(5)估计一下,2.5小时大约做多少个零件?5.5小时呢?
11、在比例尺是的地图上,两地间的距离是16厘米.
(1)两地间的实际距离是多少千米?
(2)一列火车由到用了3小时,火车每小时行多少千米?
12、一个房间,用边长3分米的方砖铺地,需要432块,如果改用边长4分米的方砖铺地,需要多少块?
13、从儿童节那天开始,小明读名著《红楼梦》.开始的4天他读完了32页,照这样计算,这个月小明一共可以读完多少页?(用比例规范解答)
14、小兰的身高,她的影子长是.如果同一时间,同一地点测得一棵树的影子长,这棵树有多高?
15、某小区维修线路,需停电半小时,妈妈找来一根长20厘米的蜡烛,点燃8分钟后,还剩15厘米,请问,这根蜡烛够燃烧到送电吗?(用比例知识规范解答并简要说明理由)
16、某人步行4小时走了22.4千米,照这样的速度,如果再走3小时,一共可以走多少千米?(用比例解)
17、一批零件计划每天生产42套,20天完成,实际每天多生产14套,结果提前几天就完成了任务,(用比例解)
18、一个筑路队铺一条公路,原计划每天铺1.6千米,30天铺完,实际每天比原计划多铺0.8千米,实际多少天完成?(用比例解)
答案
1、解:、甲、乙
两地相距120千米,汽车每小时所行路程时间甲、乙
两地相距120千米(一定),所以成反比例;
、圆的周长圆周率圆的直径,由于圆周率是定值,所以不成比例;
、花了的剩余的钱总钱数(一定),是和一定,所以不成比例;
、正方体的表面积一个面的面积(一定),所以成正比例.
故答案为:,.
2、解:(1)速度时间路程(一定),是乘积一定
所以当路程一定时,速度与时间成反比例.
(2)图上距离:实际距离比例尺(一定),是比值一定
所以当比例尺一定时,图上距离与实际距离成正比例
(3)用去的吨数剩下的吨数煤的总吨数(一定),既不是乘积一定也不是比值一定.
所以当煤的总吨数一定时,用去的吨数与剩下的吨数不成比例.
故答案为:反,正,不成.
3、解:如果,、均不为,即,是比值一定,则和成正比例;
如果,即,是乘积一定,那么和成反比例.
故答案为:正,反.
4、解:因为子中,如果一定,
即比值一定,所以和成正比例;
因为
所以,所以如果一定,即乘积一定,所以和成反比例.
故答案为:正,反.
5、解:如果,则(一定),则和成
反比例;
如果,即(一定),所以和成
正比例
故答案为:反,正.
6、解:(1)所作图象如下图,观察发现:表示树高和对应影长的点,都在一条直线上.
(2)连线以后,发现表示树高和对应影长的点,都在一条直线上,这说明树高和影长成正比例关系,
因为随着树的高度的增加,影长也在增加,且树高与影长的商是一定的,所以树高和影长成正比例关系;
(3)设树高8时,影长为米,影长时,树高米,
则有
;
答:树高时,影长6.4米,影长时,树高5米.
故答案为:在、正比例;
6.4,5.
7、解:(1)2厘米:50千米
厘米:5000000厘米
4厘米:100千米
厘米:10000000厘米
因为比例尺(一定)
所以图上距离和实际距离成正比例.
(2)2厘米:50千米
厘米:5000000厘米
,
答:这幅地图的比例尺是.
(3)
(厘米),
30000000厘米千米,
答:两地的实际距离是300千米.
故答案为:正比例;.
8、解:(1)
,
,
,
填表如下:
实际高度
影长
实际高度与影长的比值
竹竿
1
2
0.5
4
竹竿
2
1.6
0.4
4
木棒
1
1
0.25
4
(2)仔细观察表格中竹竿、木棒的实际高度与影长的比值,,发现比值是比值一定,所以实际高度与影长之间成正比例;
(3)(米;
答:旗杆的实际高度应是12.8米,
故答案为:12.8.
9、解:(1)因为两种量是否是对应的比值一定
所以两个车间生产零件的个数分别与它们所用的时间成正比例.
(2)乙车间生产9天后赶上甲车间生产的个数,甲、乙两个车间完成任务时,甲车间所用的时间多.
(3)(个
(个
答:高.
故答案为:正,9,甲,50,乙,25.
10、解:(1)
时间时
1
2
4
6
8
12
数量个
25
50
100
150
200
300
(2)
(3)我发现加工零件的时间和数量成正比例关系.
(4)加工零件的时间和数量成正比例关系
(5)(个
(个
答:2.5小时大约做63个零件,5.5小时大约做138个零件.
11、解:(1)(厘米);
96000000厘米(千米);
(2)(千米);
答:两地间的实际距离是960千米,火车每小时行320千米.
12、解:设需要块.
;
答:需要243块.
13、解:设小明一个月天)可以页书,
,
,
,
;
答:这个月小明一共可以读完240页.
14、解:设这棵树的高为米,
,
,
,
.
答:这棵树有2.5米.
15、解:20厘米的蜡烛燃烧所用的时间为分钟,
,
,
,
,
,
因为半小时分钟,
,
所以这根蜡烛够燃烧到送电;
答:这根蜡烛够燃烧到送电.
16、解;设一共可以走千米,
,
,
,
,
.
答:一共可以走39.2千米.
17、解:设可以提前天完成.
,
,
;
答:可以提前5天完成.
18、解:设实际天完成,
则,
,
;
答:实际20天完成.
