1.6 利用三角函数测高同步练习(含解析)
文档属性
| 名称 | 1.6 利用三角函数测高同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 11:17:06 | ||
图片预览



文档简介
1.7利用三角函数测高
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,其中选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020?石家庄二模)如图,嘉琪在一座桥的附近试飞一架小型无人机,为了测量无人机飞行的高度AD,嘉琪通过操控装置测得无人机俯视桥头B,C的俯角分别为∠EAB=60°和∠EAC=30°,且D、B、C在同一水平线上.已知桥BC=30米,则无人机的飞行高度AD=( )
A.15米 B.153米 C.(153-15)米 D.(153+15)米
2.(2020?深圳模拟)如图所示,从一热气球的探测器A点,看一栋高楼顶部B点的仰角为30°,看这栋高楼底部C点的俯角为60°,若热气球与高楼的水平距离为30m,则这栋高楼高度是( )
A.60m B.403m C.303m D.603m
3.(2020春?南岸区校级月考)如图所示,林克想测量一座传送塔的高度,但是塔周围有怪物无法接近.于是他先在传送塔周围的空地C处的地面上水平放置了一个小平面镜,然后他沿着BC方向移动,当移动到点E时.他刚好在小平面镜内看到这座传送塔的顶端A的像,此时,测得顶端A的仰角为32°,CE=2米,林克眼睛与地面的距离DE=1.6米,已知点B、C、E在同一水平直线上,且DE、AB均垂直于BE,若小平面镜的大小忽略不计,则这座传送塔的高度AB是( )米.(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.64)
A.14.4 B.15.4 C.16.2 D.17.5
4.(2020春?北碚区校级月考)学校某数学兴趣小组想测学校旗杆高度如图,明明在稻香园一楼A点测得旗杆顶点F仰角为45°,在稻香园二楼B点测得点F的仰角为37°.明明从A点朝旗杆方向步行4米到C点,沿坡度i=1:3的台阶走到点D,再向前走5米到旗杆底部E,已知稻香园AB高度为4.5米,则旗杆EF的高度约为( )(参考数据:sin37°=0.6,cos37°=0.8,tan37°=0.75)
A.13.5米 B.15米 C.16.5米 D.18米
5.(2020?渝中区校级三模)如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是27°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°,若斜坡AF的坡度i=1:3,则大树的高度为( )(结果保留整数,参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.5,sin48°≈0.74,cos48°≈0.67,tan48°≈1.1,3≈1.7)
A.8米 B.9米 C.10米 D.11米
6.(2020?渝中区校级二模)保利观澜旁边有一望江公园,公园里有一文峰塔,工程人员在与塔底中心的D同一水平线的A处,测得AD=20米,沿坡度i=0.75的斜坡AB走到B点,测得塔顶E仰角为37°,再沿水平方向走20米到C处,测得塔顶E的仰角为22°,则塔高DE为( )米.(结果精确到十分位)(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,)
A.18.3米 B.19.3米 C.20米 D.21.2米
7.(2020?大东区二模)小明同学在校外实践活动中对一座大桥开展测量活动.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=m,则此时大桥主架顶端离水面的高CD为( )
A.msinα+msinβ B.mcosα+mcosβ
C.mtanα+mtanβ D.mtanα+mtanβ
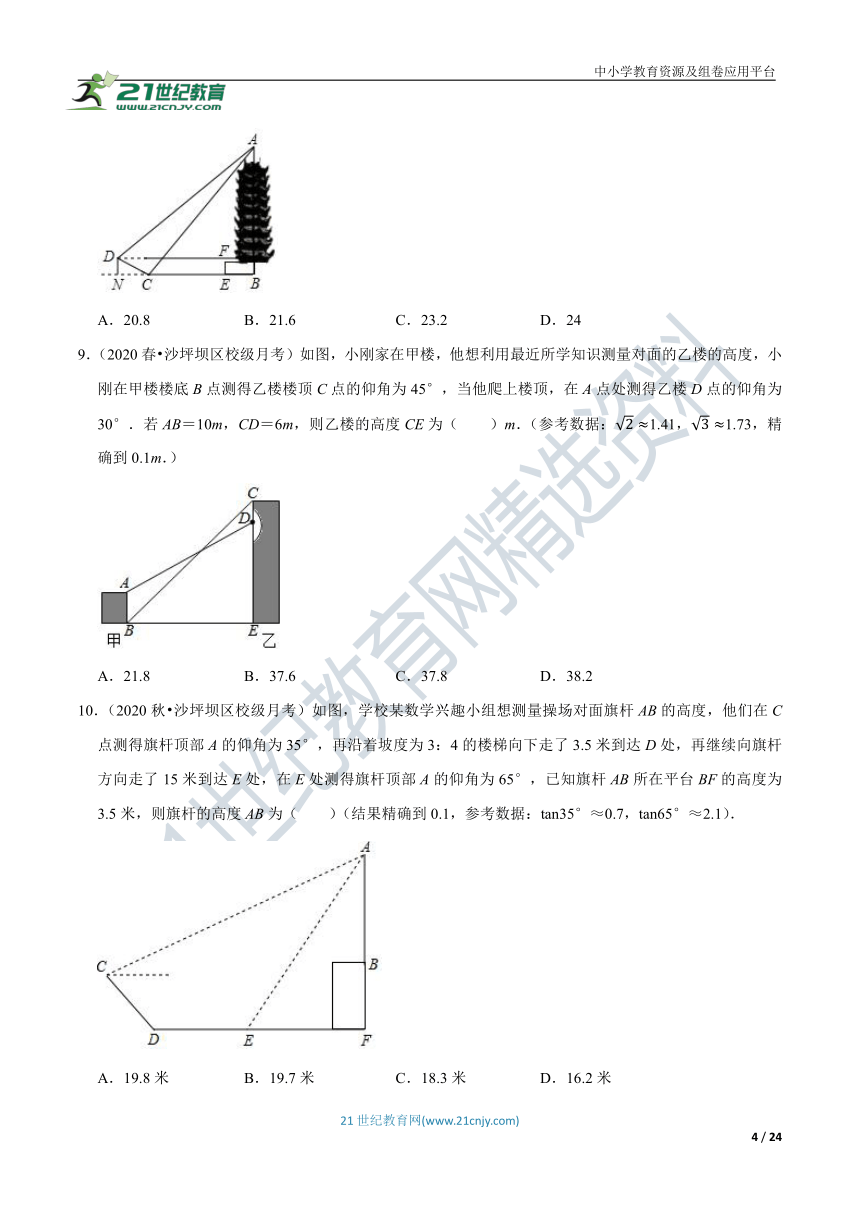
8.(2020?沙坪坝区校级一模)碧津公园坐落在江北机场旁,它是一个风景秀丽、优美如画的公园.园中的碧津塔是一座八角塔,每个角挂有一个风铃,被评为重庆市公园最美景点.重庆一中某数学兴趣小组,想测量碧津塔的高度,他们在点C处测得碧津塔顶部A处的仰角为45°,再沿着坡度为i=1:2.4的斜坡CD向上走了5.2米到达点D,此时测得碧津塔顶部A的仰角为37°,碧津塔AB所在平台高度EF为0.8米.A、B、C、D、E、F在同一平面内,则碧津塔AB的高约为( )米(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
A.20.8 B.21.6 C.23.2 D.24
9.(2020春?沙坪坝区校级月考)如图,小刚家在甲楼,他想利用最近所学知识测量对面的乙楼的高度,小刚在甲楼楼底B点测得乙楼楼顶C点的仰角为45°,当他爬上楼顶,在A点处测得乙楼D点的仰角为30°.若AB=10m,CD=6m,则乙楼的高度CE为( )m.(参考数据:2≈1.41,3≈1.73,精确到0.1m.)
A.21.8 B.37.6 C.37.8 D.38.2
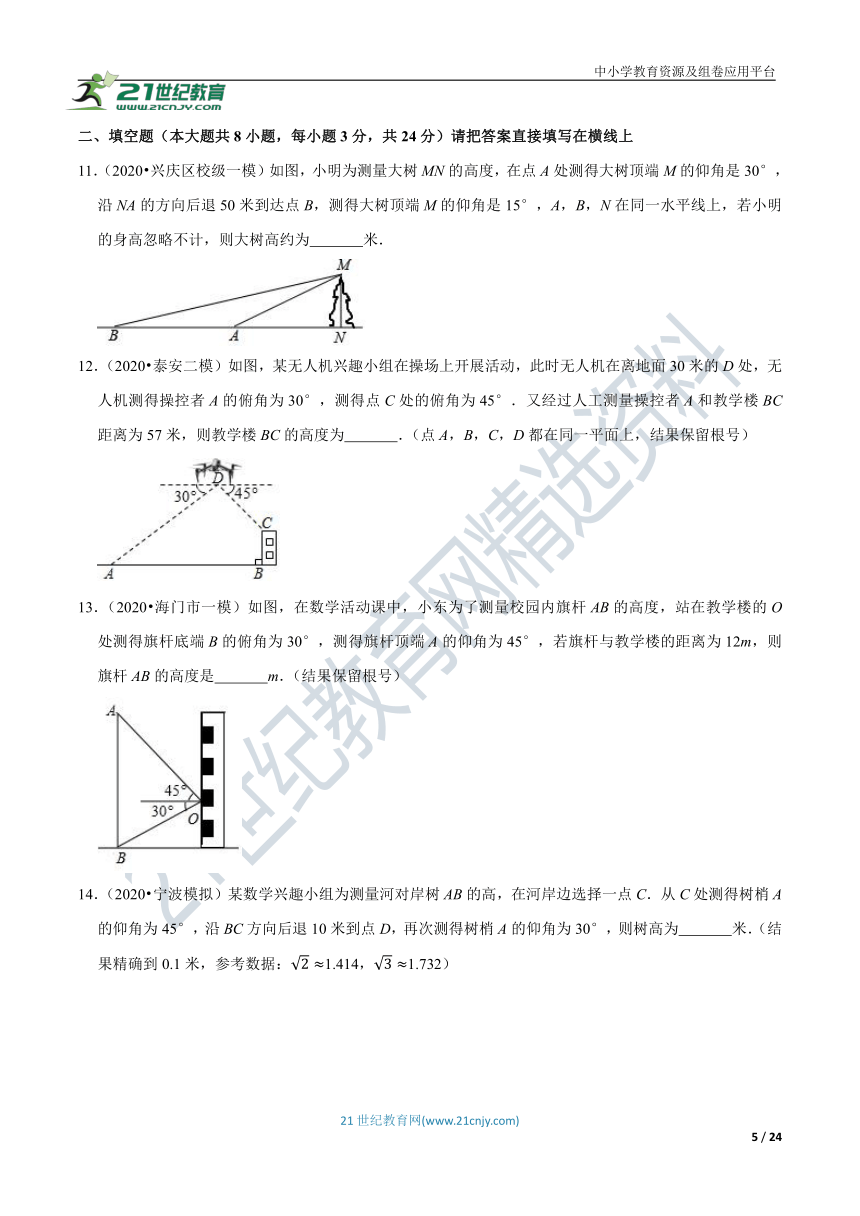
10.(2020秋?沙坪坝区校级月考)如图,学校某数学兴趣小组想测量操场对面旗杆AB的高度,他们在C点测得旗杆顶部A的仰角为35°,再沿着坡度为3:4的楼梯向下走了3.5米到达D处,再继续向旗杆方向走了15米到达E处,在E处测得旗杆顶部A的仰角为65°,已知旗杆AB所在平台BF的高度为3.5米,则旗杆的高度AB为( )(结果精确到0.1,参考数据:tan35°≈0.7,tan65°≈2.1).
A.19.8米 B.19.7米 C.18.3米 D.16.2米
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020?兴庆区校级一模)如图,小明为测量大树MN的高度,在点A处测得大树顶端M的仰角是30°,沿NA的方向后退50米到达点B,测得大树顶端M的仰角是15°,A,B,N在同一水平线上,若小明的身高忽略不计,则大树高约为 米.
12.(2020?泰安二模)如图,某无人机兴趣小组在操场上开展活动,此时无人机在离地面30米的D处,无人机测得操控者A的俯角为30°,测得点C处的俯角为45°.又经过人工测量操控者A和教学楼BC距离为57米,则教学楼BC的高度为 .(点A,B,C,D都在同一平面上,结果保留根号)
13.(2020?海门市一模)如图,在数学活动课中,小东为了测量校园内旗杆AB的高度,站在教学楼的O处测得旗杆底端B的俯角为30°,测得旗杆顶端A的仰角为45°,若旗杆与教学楼的距离为12m,则旗杆AB的高度是 m.(结果保留根号)
14.(2020?宁波模拟)某数学兴趣小组为测量河对岸树AB的高,在河岸边选择一点C.从C处测得树梢A的仰角为45°,沿BC方向后退10米到点D,再次测得树梢A的仰角为30°,则树高为 米.(结果精确到0.1米,参考数据:2≈1.414,3≈1.732)
15.(2020春?太原期中)如图,小亮为了测量校园里教学楼AB的高度,他站在离教学楼30m的C处仰望教学楼顶部A,仰角为30°.已知小亮的高度是1.6m,则教学楼的高度约为 m(3≈1.7,结果精确到0.1).
16.(2020?闵行区二模)七宝琉璃玲珑塔(简称七宝塔),位于上海市七宝古镇的七宝教寺内,塔高47米,共7层.学校老师组织学生利用无人机实地勘测,如果无人机在飞行的某一高度时传回数据,测得塔顶的仰角为60°,塔底的俯角为45°,那么此时无人机距离地面的高度为 米.(结果保留根号)
17.(2020?镇平县模拟)如图,某地修建高速公路,要从A地向B地修一条隧道(点A、B在同一水平面上)为了测量A、B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为α,则A、B两地之间的距离为 米.
18.(2020春?新泰市期中)如图,某建筑物的顶部有一块标识牌CD,小明在斜坡上B处测得标识牌顶部C的仰角为45°,沿斜坡走下来,在地面A处测得标识牌底部D的仰角为60°,已知斜坡AB的坡角为30°,AB=AE=10米.则标识牌CD的高度是 米.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020?新昌县校级模拟)如图,某学校体育场看台的顶端C到地面的垂直距离CD为2m,看台所在斜坡CM的坡比i=1:3,在点C处测得旗杆顶点A的仰角为30°,在点M处测得旗杆顶点A的仰角为60°,且B,M,D三点在同一水平线上.
(1)求DM的长.
(2)求旗杆AB的高度.(结果保留根号)
20.(2020春?辉南县校级月考)如图,已知线段AB、CD分别表示甲、乙两栋楼的高,AB⊥BD,CD⊥BD,甲楼的高AB=24米.从甲楼顶部A处测得乙楼顶部C的仰角α=30°,测得乙楼底部D的俯角β=60°.求乙楼的高CD.
21.(2020春?亭湖区校级月考)如图,随着社会经济的发展,人们的环境保护意识也在逐步增强.某社区设立了“保护环境爱我地球“的宣传牌,已知立杆AB的高度是4m,从地面上某处D点测得宣传牌顶端C和底端B点的仰角分别是62°和45°、求宜传牌的高度BC的长.(精确到0.1m,参考数据:sin62°=0.83,cos62°=0.47,tan62°=1.88)
22.(2020春?吴兴区校级期中)第十一届全国少数民族传统体育运动会于2019年9月8日至16日在郑州举行,据了解,该赛事每四年举办一届,是我国规格最高、规模最大的综合性民族体育盛会,其中,花炮、押加、民族式摔跤三个项目的比赛在郑州大学主校区进行.如图,钟楼是郑州大学主校区标志性建筑物之一,是郑大的“第一高度”,寓意来自五湖四海的郑大人的团结和凝聚.小刚站在钟楼前C处测得钟楼顶A的仰角为53°,小强站在对面的教学楼三楼上的D处测得钟楼顶A的仰角为45°,此时,两人的水平距离EC为4m,已知教学楼三楼所在的高度为10m,根据测得的数据,计算钟楼AB的高度.
(参考数据:sin53°≈45,cos53°≈35,tan53°≈43)
23.(2020?安宁区校级模拟)兰州白塔山山势起伏,山中白塔七级八面,上有绿项,下筑圆基,几经强烈地震仍屹立未动,显示了我国古代劳动人民在建筑艺术上的智慧与才能.
问题提出:如何测量白塔的高MN.
方案设计:九年级三班的白亮同学去测量白塔的高,如图,他在点A处测得塔尖M的仰角是30°,向前走了50米到达点B处,又测得塔尖M的仰角是60°.
问题解决:根据上述方案和数据,求白塔的高度MN(结果精确到1m,参考数据:3≈1.73).
24.(2020?中原区校级模拟)某数学兴趣小组学过锐角三角函数后,计划测量中原福塔的总高度.如图所示,在B处测得福塔主体建筑顶点A的仰角为45°,福塔顶部桅杆天线AD高120m,再沿CB方向前进20m到达E处,测得桅杆天线顶部D的仰角为53.4°.求中原福塔CD的总高度.(结果精确到1m.参考数据:sin53.4°≈0.803,cos53.4°≈0.596,tan53.4°≈1.346)
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.
【解答】解:∵∠EAB=60°,∠EAC=30°,
∴∠CAD=60°,∠BAD=30°,
∴CD=AD?tan∠CAD=3AD,BD=AD?tan∠BAD=33AD,
∴BC=CD﹣BD=233AD=30,
∴AD=153(米).
答:无人机的飞行高度AD为153米.
故选:B.
2.
【解答】解:过A作AD⊥BC,垂足为D
在Rt△ABD中,∵∠BAD=30°,AD=30m,
∴BD=AD?tan30°=30×33=103(m),
在Rt△ACD中,∵∠CAD=60°,AD=30m,
∴CD=AD?tan60°=30×3=303(m),
∴BC=BD+CD=103+303=403(m),
即这栋高楼高度是403m.
故选:B.
3.
【解答】解:作DF⊥AB于F,如图:
则DF=EB,BF=DE=1.6,
由题意得:∠ADF=32°,∠DCE=∠ACB,∠DEC=∠ABC=90°,
∴△CDE∽△CAB,
∴DECE=1.62=45=ABBC,
设AB=4x,则BC=5x,
∴DF=EB=CE+BC=2+5x,AF=AB﹣BF=4x﹣1.6,
在Rt△ADF中,tan∠ADF=tan32°≈0.64=AFDF,
即4x-1.62+5x=0.64,
解得:x=3.6,
∴AB=14.4(米);
故选:A.
4.
【解答】解:延长FE、AC交于点G,作DH⊥AG于H,BM⊥FE于M,如图所示:
则BM=AG,GM=AB=4.5,GH=DE=5,EG=DH,∠MBF=37°,∠GAF=45°,
∴△AFG是等腰直角三角形,
∴FG=AG=BM,
∵CD的坡度i=1:3,
∴DHCH=1:3,
∴CH=3DH,
设EG=DH=x,则CH=3x,
∴BM=FG=AG=GH+CH+AC=5+3x+4=9+3x,
∴FM=FG﹣GM=9+3x﹣4.5=4.5+3x,
在Rt△BFM中,tan∠MBF=FMBM=tan37°=0.75,
∴4.5+3x9+3x=34,
解得:x=3,
∴FG=18,EG=3,
∴EF=FG﹣EG=18﹣3=15(米);
故选:B.
5.
【解答】解:过点D作DM⊥BC于点M,DN⊥AC于点N,
则四边形DMCN是矩形,
∵DA=6,斜坡AF的坡比i=1:3=33=tan∠DAN,
∴∠DAN=30°,DN=12AD=3,AN=3DN=33,
设大树的高度为x米,
∵在斜坡上A处测得大树顶端B的仰角是48°,
∴tan48°=BCAC≈1.1,
∴AC=x1.1,
∴DM=CN=AN+AC=33+x1.1,
在△BDM中,tan∠BDM=BMDM=tan27°≈0.5,
∴BM=0.5DM,
∴x﹣3=0.5×(33+x1.1),
解得:x≈10.
即树高BC约10米.
故选:C.
6.
【解答】解:连接DE,作BF⊥DE于F,BG⊥DA于G,如图:
则DF=BG,BF=DG=AD+AG,
∵AB=斜坡AB的坡度i=0.75=BGAG,
∴设BG=3xm,则AG=4xm,BF=DG=20+4x(m),CF=BF+BC=20+4x+20=40+4x(m),
由题意得:∠EBF=37°,∠ECF=22°,
∵tan∠BEF=EFBF=EF20+4x,tan∠ECF=EFCF=EF40+4x,
∴EF=tan37°(20+4x),EF=tan22°(40+4x),
∴0.75(20+4x)=0.40(40+4x),
解得:x=57,
∴DF=BG=3x=157(m),
EF=0.40(40+4x)=1207(m),
∴DE=DF+EF=157+1207≈19.3(m);
故选:B.
7.
【解答】解:∵在Rt△ABC中,tanα=BCAB,
∴BC=AB?tanα=mtanα,
在Rt△ABD中,tanβ=BDAB,
∴BD=AB?tanβ=mtanβ,
∴CD=BC+BD=mtanα+mtanβ.
故选:C.
8.
【解答】解:根据题意可知:
∠ABC=90°,∠ACB=45°,
∴AB=BC,
∵DN:NC=i=1:2.4,CD=5.2,
∴DN=2,CN=4.8,
设DG⊥AB,垂足为G,
∴在Rt△ADG中,∠ADG=37°,
∵AG=AB﹣GB=AB﹣DN=AB﹣2,
又DG=BN=CN+BC=4.8+AB,
∴tan∠ADG=AGDG,
∴34×(4.8+AB)=AB﹣2,
解得AB=22.4,
∵AB所在平台高度EF为0.8米,
∴22.4﹣0.8=21.6(米).
答:碧津塔AB的高约为21.6米.
故选:B.
9.
【解答】解:如图,过点A作AF⊥CE于点F,
根据题意可知:
AB⊥BE,CE⊥BE,
∴四边形ABEF是矩形,
∴AF=BE,EF=AB=10,
在Rt△CBE中,∠CBE=45,
∴BE=CE=CD+DF+FE=6+DF+10=16+DF,
在Rt△ADF中,∠DAF=30°,
∴DF=AF?tan30°,
∴DF=(16+DF)×33,
解得DF=8(3+1),
∴CE=16+DF=24+83≈37.8(m).
答:乙楼的高度CE为37.8m.
故选:C.
10.
【解答】解:作CG⊥AF于G,DH⊥CG于H,如图所示:
则HG=DF,FG=DH,
∵楼梯CD的坡度为3:4,CD=3.5,
∴FG=DH=2.1,CH=2.8,
在Rt△ACG中,∠ACG=35°,tan∠ACG=AGCG=tan35°≈0.7,
∴AG≈0.7CG,
∴AF=AG+FG=0.7CG+2.1,
∵DF=HG=CG﹣CH=CG﹣2.8,
∴EF=DF﹣DE=CG﹣2.8﹣15=CG﹣17.8,
在Rt△AEF中,∠AEF=65°,tan∠AEF=AFEF=tan65°≈2.1,
∴AF=2.1EF,
∴0.7CG+2.1=2.1(CG﹣17.8),
解得:CG=28.2,
∴AF=0.7×28.2+2.1=21.84,
∴AB=AF﹣BF=21.84﹣3.5≈18.3(米),
即旗杆的高度AB约为18.3米;
故选:C.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.
【解答】解:∠MAN是△ABM的一个外角,
∴∠AMB=∠MAN﹣∠ABM=30°﹣15°=15°,
∴∠AMB=∠ABM,
∴AM=AB=50米,
在Rt△AMN中,∠MAN=30°,
∴MN=12AM=25米;
故答案为:25.
12.
【解答】解:过点D作DE⊥AB于点E,过点C作CF⊥DE于点F.
由题意得,AB=57,DE=30,∠A=30°,∠DCF=45°.
在Rt△ADE中,∠AED=90°,
∴tan30°=DEAE,
即33=30AE,
∴AE=303,
∵AB=57,
∴BE=AB﹣AE=57﹣303,
∵四边形BCFE是矩形,
∴CF=BE=57﹣303.
在Rt△DCF中,∠DFC=90°,
∴∠CDF=∠DCF=45°.
∴DF=CF=57﹣303,
∴BC=EF=30﹣57+303=(303-27)米.
答:教学楼BC高约(303-27)米.
故答案为:(303-27)米.
13.
【解答】解:如图,作OC⊥AB于点C,
∴∠ACO=∠BCO=90°,
根据题意可知:
∠AOC=45°,∠BOC=30°,OC=12,
∴AC=OC=12,
∴BC=OC?tan30°=12×33=43.
∴AB=AC+BC=12+43(m).
所以旗杆AB的高度是(12+43)m.
故答案为:(12+43).
14.
【解答】解:根据题意可知:
∠ABC=90°,CD=10,
在Rt△ABC中,∠ACB=45°,
∴AB=CB,
在Rt△ABD中,∠ADB=30°,BD=CD+BC=10+AB,
∴tan30°=ABBD,
即33=AB10+AB,
解得AB≈13.7(米).
答:树高约为13.7米.
故答案为:13.7
15.
【解答】解:如图,作DE⊥AB于点E,
根据题意可知:
DC⊥BC,AB⊥BC,
∴四边形DCBE是矩形,
∴BE=DC=1.6,DE=CB=30,
∴在Rt△ADE中,∠ADE=30°,DE=30,
∴AE=DE?tan30°=30×33=103≈17(m).
答:教学楼的高度约为17m.
故答案为:17.
16.
【解答】解:如图所示:设无人机所在位置为点A,
根据题意可知:
∠BAD=60°,∠DAC=45°,BC=47(米),
设此时无人机距离地面的高度为x米,
则CD=x,则BD=47﹣x,AD=CD=x,
在Rt△ADB中,tan60°=BDAD,
即3=47-xx,
解得x=473-472(米).
答:此时无人机距离地面的高度为473-472米.
故答案为:473-472.
17.
【解答】解:在Rt△ABC中,∵∠CAB=90°,∠B=α,AC=800米,
∴tanα=ACAB,
∴AB=ACtanα=800tanα(米).
故答案为:800tanα.
18.
【解答】解:如图,过点B作BH⊥AE于点H,BF⊥CE于点F,
根据题意可知:
∠BAH=30°,
AB=AE=10,
∴BH=5,AH=53,
∵CE⊥AE,
∴四边形BHEF是矩形,
∴EF=BH=5,
BF=HE=AH+AE=53+10,
∵∠DAE=60°,
∴DE=AE?tan60°=103,
∴DF=DE﹣EF=103-5,
∵∠CBF=45°,
∴CF=BF=53+10,
∴CD=CF﹣DF=53+10﹣(103-5)=15﹣53(米).
所以标识牌CD的高度是(15﹣53)米.
故答案为:(15﹣53).
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.
【解答】解:(1)∵CD=2,tan∠CMD=13,
∴MD=6m;
(2)过点C作CE⊥AB于点E,
设BM=x,
∴BD=x+6,
∵∠AMB=60°,
∴∠BAM=30°,
∴AB=3x,
已知四边形CDBE是矩形,
∴BE=CD=2,CE=BD=x+6,
∴AE=3x﹣23
在Rt△ACE中,
∵tan30°=AECE,
∴13=3x-2x+6,
解得:x=3+3,
∴AB=3x=3+33≈8.2m.
20.
【解答】解:∵AB⊥BD,CD⊥BD,
∴四边形ABDE是矩形,
∴DE=AB=24m,
在Rt△AED中,AE=EDtanβ=243=83(m),
在Rt△ACE中,CE=AE?tanα=83×33=8(m),
∴CD=DE+CE=24+8=32(m).
答:乙楼CD的高为32m.
21.
【解答】解:在Rt△ADB中,
∵∠BDA=45°,
∴AD=AB=4m.
在Rt△ADC中,AC=AD?tan62°≈4×1.88=7.52(m).
∴BC=AC﹣AB=7.52﹣4=3.52≈3.5(m).
答:宣传牌BC的高度是3.5m.
22.
【解答】解:作DF⊥AB于F,
设AB=xm,
∵FB⊥EB,DE⊥EB,DF⊥AB,
∴四边形FBED为矩形,
∴FB=DE=10,DF=BE,
∴AF=10﹣x,
在Rt△AFD中,∠ADF=45°,
∴DF=AF=x﹣10,
在Rt△ABC中,∠ACB=53°,tan∠ACB=ABBC,
∴BC=ABtan∠ACB≈34x,
由题意得,BE﹣BC=CE,即x﹣10-34x=4,
解得,x=56,
答:钟楼AB的高度约为56m.
23.
【解答】解:∵∠MBN是△ABM的一个外角,
∴∠AMB=∠MBN﹣∠MAB=30°,
∴∠AMB=∠MAB,
∴BM=AB=50,
在Rt△MBN中,sin∠MBN=MNMB,
∴MN=BM?sin∠MBN=50×32=253≈43,
答:白塔的高度MN约为43米.
24.
【解答】解:设AC为xm,则CD=(x+120)m,
在Rt△ACB中,∠ABC=45°,
∴BC=AC=x,
∴CE=x+20,
在Rt△DCE中,tan∠DEC=CDCE,即x+120x+20≈1.346,
解得,x≈269.0,
∴CD=x+120=389.0≈389,
答:中原福塔CD的总高度约为389m.
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,其中选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020?石家庄二模)如图,嘉琪在一座桥的附近试飞一架小型无人机,为了测量无人机飞行的高度AD,嘉琪通过操控装置测得无人机俯视桥头B,C的俯角分别为∠EAB=60°和∠EAC=30°,且D、B、C在同一水平线上.已知桥BC=30米,则无人机的飞行高度AD=( )
A.15米 B.153米 C.(153-15)米 D.(153+15)米
2.(2020?深圳模拟)如图所示,从一热气球的探测器A点,看一栋高楼顶部B点的仰角为30°,看这栋高楼底部C点的俯角为60°,若热气球与高楼的水平距离为30m,则这栋高楼高度是( )
A.60m B.403m C.303m D.603m
3.(2020春?南岸区校级月考)如图所示,林克想测量一座传送塔的高度,但是塔周围有怪物无法接近.于是他先在传送塔周围的空地C处的地面上水平放置了一个小平面镜,然后他沿着BC方向移动,当移动到点E时.他刚好在小平面镜内看到这座传送塔的顶端A的像,此时,测得顶端A的仰角为32°,CE=2米,林克眼睛与地面的距离DE=1.6米,已知点B、C、E在同一水平直线上,且DE、AB均垂直于BE,若小平面镜的大小忽略不计,则这座传送塔的高度AB是( )米.(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.64)
A.14.4 B.15.4 C.16.2 D.17.5
4.(2020春?北碚区校级月考)学校某数学兴趣小组想测学校旗杆高度如图,明明在稻香园一楼A点测得旗杆顶点F仰角为45°,在稻香园二楼B点测得点F的仰角为37°.明明从A点朝旗杆方向步行4米到C点,沿坡度i=1:3的台阶走到点D,再向前走5米到旗杆底部E,已知稻香园AB高度为4.5米,则旗杆EF的高度约为( )(参考数据:sin37°=0.6,cos37°=0.8,tan37°=0.75)
A.13.5米 B.15米 C.16.5米 D.18米
5.(2020?渝中区校级三模)如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是27°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°,若斜坡AF的坡度i=1:3,则大树的高度为( )(结果保留整数,参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.5,sin48°≈0.74,cos48°≈0.67,tan48°≈1.1,3≈1.7)
A.8米 B.9米 C.10米 D.11米
6.(2020?渝中区校级二模)保利观澜旁边有一望江公园,公园里有一文峰塔,工程人员在与塔底中心的D同一水平线的A处,测得AD=20米,沿坡度i=0.75的斜坡AB走到B点,测得塔顶E仰角为37°,再沿水平方向走20米到C处,测得塔顶E的仰角为22°,则塔高DE为( )米.(结果精确到十分位)(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,)
A.18.3米 B.19.3米 C.20米 D.21.2米
7.(2020?大东区二模)小明同学在校外实践活动中对一座大桥开展测量活动.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=m,则此时大桥主架顶端离水面的高CD为( )
A.msinα+msinβ B.mcosα+mcosβ
C.mtanα+mtanβ D.mtanα+mtanβ
8.(2020?沙坪坝区校级一模)碧津公园坐落在江北机场旁,它是一个风景秀丽、优美如画的公园.园中的碧津塔是一座八角塔,每个角挂有一个风铃,被评为重庆市公园最美景点.重庆一中某数学兴趣小组,想测量碧津塔的高度,他们在点C处测得碧津塔顶部A处的仰角为45°,再沿着坡度为i=1:2.4的斜坡CD向上走了5.2米到达点D,此时测得碧津塔顶部A的仰角为37°,碧津塔AB所在平台高度EF为0.8米.A、B、C、D、E、F在同一平面内,则碧津塔AB的高约为( )米(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
A.20.8 B.21.6 C.23.2 D.24
9.(2020春?沙坪坝区校级月考)如图,小刚家在甲楼,他想利用最近所学知识测量对面的乙楼的高度,小刚在甲楼楼底B点测得乙楼楼顶C点的仰角为45°,当他爬上楼顶,在A点处测得乙楼D点的仰角为30°.若AB=10m,CD=6m,则乙楼的高度CE为( )m.(参考数据:2≈1.41,3≈1.73,精确到0.1m.)
A.21.8 B.37.6 C.37.8 D.38.2
10.(2020秋?沙坪坝区校级月考)如图,学校某数学兴趣小组想测量操场对面旗杆AB的高度,他们在C点测得旗杆顶部A的仰角为35°,再沿着坡度为3:4的楼梯向下走了3.5米到达D处,再继续向旗杆方向走了15米到达E处,在E处测得旗杆顶部A的仰角为65°,已知旗杆AB所在平台BF的高度为3.5米,则旗杆的高度AB为( )(结果精确到0.1,参考数据:tan35°≈0.7,tan65°≈2.1).
A.19.8米 B.19.7米 C.18.3米 D.16.2米
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020?兴庆区校级一模)如图,小明为测量大树MN的高度,在点A处测得大树顶端M的仰角是30°,沿NA的方向后退50米到达点B,测得大树顶端M的仰角是15°,A,B,N在同一水平线上,若小明的身高忽略不计,则大树高约为 米.
12.(2020?泰安二模)如图,某无人机兴趣小组在操场上开展活动,此时无人机在离地面30米的D处,无人机测得操控者A的俯角为30°,测得点C处的俯角为45°.又经过人工测量操控者A和教学楼BC距离为57米,则教学楼BC的高度为 .(点A,B,C,D都在同一平面上,结果保留根号)
13.(2020?海门市一模)如图,在数学活动课中,小东为了测量校园内旗杆AB的高度,站在教学楼的O处测得旗杆底端B的俯角为30°,测得旗杆顶端A的仰角为45°,若旗杆与教学楼的距离为12m,则旗杆AB的高度是 m.(结果保留根号)
14.(2020?宁波模拟)某数学兴趣小组为测量河对岸树AB的高,在河岸边选择一点C.从C处测得树梢A的仰角为45°,沿BC方向后退10米到点D,再次测得树梢A的仰角为30°,则树高为 米.(结果精确到0.1米,参考数据:2≈1.414,3≈1.732)
15.(2020春?太原期中)如图,小亮为了测量校园里教学楼AB的高度,他站在离教学楼30m的C处仰望教学楼顶部A,仰角为30°.已知小亮的高度是1.6m,则教学楼的高度约为 m(3≈1.7,结果精确到0.1).
16.(2020?闵行区二模)七宝琉璃玲珑塔(简称七宝塔),位于上海市七宝古镇的七宝教寺内,塔高47米,共7层.学校老师组织学生利用无人机实地勘测,如果无人机在飞行的某一高度时传回数据,测得塔顶的仰角为60°,塔底的俯角为45°,那么此时无人机距离地面的高度为 米.(结果保留根号)
17.(2020?镇平县模拟)如图,某地修建高速公路,要从A地向B地修一条隧道(点A、B在同一水平面上)为了测量A、B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为α,则A、B两地之间的距离为 米.
18.(2020春?新泰市期中)如图,某建筑物的顶部有一块标识牌CD,小明在斜坡上B处测得标识牌顶部C的仰角为45°,沿斜坡走下来,在地面A处测得标识牌底部D的仰角为60°,已知斜坡AB的坡角为30°,AB=AE=10米.则标识牌CD的高度是 米.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020?新昌县校级模拟)如图,某学校体育场看台的顶端C到地面的垂直距离CD为2m,看台所在斜坡CM的坡比i=1:3,在点C处测得旗杆顶点A的仰角为30°,在点M处测得旗杆顶点A的仰角为60°,且B,M,D三点在同一水平线上.
(1)求DM的长.
(2)求旗杆AB的高度.(结果保留根号)
20.(2020春?辉南县校级月考)如图,已知线段AB、CD分别表示甲、乙两栋楼的高,AB⊥BD,CD⊥BD,甲楼的高AB=24米.从甲楼顶部A处测得乙楼顶部C的仰角α=30°,测得乙楼底部D的俯角β=60°.求乙楼的高CD.
21.(2020春?亭湖区校级月考)如图,随着社会经济的发展,人们的环境保护意识也在逐步增强.某社区设立了“保护环境爱我地球“的宣传牌,已知立杆AB的高度是4m,从地面上某处D点测得宣传牌顶端C和底端B点的仰角分别是62°和45°、求宜传牌的高度BC的长.(精确到0.1m,参考数据:sin62°=0.83,cos62°=0.47,tan62°=1.88)
22.(2020春?吴兴区校级期中)第十一届全国少数民族传统体育运动会于2019年9月8日至16日在郑州举行,据了解,该赛事每四年举办一届,是我国规格最高、规模最大的综合性民族体育盛会,其中,花炮、押加、民族式摔跤三个项目的比赛在郑州大学主校区进行.如图,钟楼是郑州大学主校区标志性建筑物之一,是郑大的“第一高度”,寓意来自五湖四海的郑大人的团结和凝聚.小刚站在钟楼前C处测得钟楼顶A的仰角为53°,小强站在对面的教学楼三楼上的D处测得钟楼顶A的仰角为45°,此时,两人的水平距离EC为4m,已知教学楼三楼所在的高度为10m,根据测得的数据,计算钟楼AB的高度.
(参考数据:sin53°≈45,cos53°≈35,tan53°≈43)
23.(2020?安宁区校级模拟)兰州白塔山山势起伏,山中白塔七级八面,上有绿项,下筑圆基,几经强烈地震仍屹立未动,显示了我国古代劳动人民在建筑艺术上的智慧与才能.
问题提出:如何测量白塔的高MN.
方案设计:九年级三班的白亮同学去测量白塔的高,如图,他在点A处测得塔尖M的仰角是30°,向前走了50米到达点B处,又测得塔尖M的仰角是60°.
问题解决:根据上述方案和数据,求白塔的高度MN(结果精确到1m,参考数据:3≈1.73).
24.(2020?中原区校级模拟)某数学兴趣小组学过锐角三角函数后,计划测量中原福塔的总高度.如图所示,在B处测得福塔主体建筑顶点A的仰角为45°,福塔顶部桅杆天线AD高120m,再沿CB方向前进20m到达E处,测得桅杆天线顶部D的仰角为53.4°.求中原福塔CD的总高度.(结果精确到1m.参考数据:sin53.4°≈0.803,cos53.4°≈0.596,tan53.4°≈1.346)
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.
【解答】解:∵∠EAB=60°,∠EAC=30°,
∴∠CAD=60°,∠BAD=30°,
∴CD=AD?tan∠CAD=3AD,BD=AD?tan∠BAD=33AD,
∴BC=CD﹣BD=233AD=30,
∴AD=153(米).
答:无人机的飞行高度AD为153米.
故选:B.
2.
【解答】解:过A作AD⊥BC,垂足为D
在Rt△ABD中,∵∠BAD=30°,AD=30m,
∴BD=AD?tan30°=30×33=103(m),
在Rt△ACD中,∵∠CAD=60°,AD=30m,
∴CD=AD?tan60°=30×3=303(m),
∴BC=BD+CD=103+303=403(m),
即这栋高楼高度是403m.
故选:B.
3.
【解答】解:作DF⊥AB于F,如图:
则DF=EB,BF=DE=1.6,
由题意得:∠ADF=32°,∠DCE=∠ACB,∠DEC=∠ABC=90°,
∴△CDE∽△CAB,
∴DECE=1.62=45=ABBC,
设AB=4x,则BC=5x,
∴DF=EB=CE+BC=2+5x,AF=AB﹣BF=4x﹣1.6,
在Rt△ADF中,tan∠ADF=tan32°≈0.64=AFDF,
即4x-1.62+5x=0.64,
解得:x=3.6,
∴AB=14.4(米);
故选:A.
4.
【解答】解:延长FE、AC交于点G,作DH⊥AG于H,BM⊥FE于M,如图所示:
则BM=AG,GM=AB=4.5,GH=DE=5,EG=DH,∠MBF=37°,∠GAF=45°,
∴△AFG是等腰直角三角形,
∴FG=AG=BM,
∵CD的坡度i=1:3,
∴DHCH=1:3,
∴CH=3DH,
设EG=DH=x,则CH=3x,
∴BM=FG=AG=GH+CH+AC=5+3x+4=9+3x,
∴FM=FG﹣GM=9+3x﹣4.5=4.5+3x,
在Rt△BFM中,tan∠MBF=FMBM=tan37°=0.75,
∴4.5+3x9+3x=34,
解得:x=3,
∴FG=18,EG=3,
∴EF=FG﹣EG=18﹣3=15(米);
故选:B.
5.
【解答】解:过点D作DM⊥BC于点M,DN⊥AC于点N,
则四边形DMCN是矩形,
∵DA=6,斜坡AF的坡比i=1:3=33=tan∠DAN,
∴∠DAN=30°,DN=12AD=3,AN=3DN=33,
设大树的高度为x米,
∵在斜坡上A处测得大树顶端B的仰角是48°,
∴tan48°=BCAC≈1.1,
∴AC=x1.1,
∴DM=CN=AN+AC=33+x1.1,
在△BDM中,tan∠BDM=BMDM=tan27°≈0.5,
∴BM=0.5DM,
∴x﹣3=0.5×(33+x1.1),
解得:x≈10.
即树高BC约10米.
故选:C.
6.
【解答】解:连接DE,作BF⊥DE于F,BG⊥DA于G,如图:
则DF=BG,BF=DG=AD+AG,
∵AB=斜坡AB的坡度i=0.75=BGAG,
∴设BG=3xm,则AG=4xm,BF=DG=20+4x(m),CF=BF+BC=20+4x+20=40+4x(m),
由题意得:∠EBF=37°,∠ECF=22°,
∵tan∠BEF=EFBF=EF20+4x,tan∠ECF=EFCF=EF40+4x,
∴EF=tan37°(20+4x),EF=tan22°(40+4x),
∴0.75(20+4x)=0.40(40+4x),
解得:x=57,
∴DF=BG=3x=157(m),
EF=0.40(40+4x)=1207(m),
∴DE=DF+EF=157+1207≈19.3(m);
故选:B.
7.
【解答】解:∵在Rt△ABC中,tanα=BCAB,
∴BC=AB?tanα=mtanα,
在Rt△ABD中,tanβ=BDAB,
∴BD=AB?tanβ=mtanβ,
∴CD=BC+BD=mtanα+mtanβ.
故选:C.
8.
【解答】解:根据题意可知:
∠ABC=90°,∠ACB=45°,
∴AB=BC,
∵DN:NC=i=1:2.4,CD=5.2,
∴DN=2,CN=4.8,
设DG⊥AB,垂足为G,
∴在Rt△ADG中,∠ADG=37°,
∵AG=AB﹣GB=AB﹣DN=AB﹣2,
又DG=BN=CN+BC=4.8+AB,
∴tan∠ADG=AGDG,
∴34×(4.8+AB)=AB﹣2,
解得AB=22.4,
∵AB所在平台高度EF为0.8米,
∴22.4﹣0.8=21.6(米).
答:碧津塔AB的高约为21.6米.
故选:B.
9.
【解答】解:如图,过点A作AF⊥CE于点F,
根据题意可知:
AB⊥BE,CE⊥BE,
∴四边形ABEF是矩形,
∴AF=BE,EF=AB=10,
在Rt△CBE中,∠CBE=45,
∴BE=CE=CD+DF+FE=6+DF+10=16+DF,
在Rt△ADF中,∠DAF=30°,
∴DF=AF?tan30°,
∴DF=(16+DF)×33,
解得DF=8(3+1),
∴CE=16+DF=24+83≈37.8(m).
答:乙楼的高度CE为37.8m.
故选:C.
10.
【解答】解:作CG⊥AF于G,DH⊥CG于H,如图所示:
则HG=DF,FG=DH,
∵楼梯CD的坡度为3:4,CD=3.5,
∴FG=DH=2.1,CH=2.8,
在Rt△ACG中,∠ACG=35°,tan∠ACG=AGCG=tan35°≈0.7,
∴AG≈0.7CG,
∴AF=AG+FG=0.7CG+2.1,
∵DF=HG=CG﹣CH=CG﹣2.8,
∴EF=DF﹣DE=CG﹣2.8﹣15=CG﹣17.8,
在Rt△AEF中,∠AEF=65°,tan∠AEF=AFEF=tan65°≈2.1,
∴AF=2.1EF,
∴0.7CG+2.1=2.1(CG﹣17.8),
解得:CG=28.2,
∴AF=0.7×28.2+2.1=21.84,
∴AB=AF﹣BF=21.84﹣3.5≈18.3(米),
即旗杆的高度AB约为18.3米;
故选:C.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.
【解答】解:∠MAN是△ABM的一个外角,
∴∠AMB=∠MAN﹣∠ABM=30°﹣15°=15°,
∴∠AMB=∠ABM,
∴AM=AB=50米,
在Rt△AMN中,∠MAN=30°,
∴MN=12AM=25米;
故答案为:25.
12.
【解答】解:过点D作DE⊥AB于点E,过点C作CF⊥DE于点F.
由题意得,AB=57,DE=30,∠A=30°,∠DCF=45°.
在Rt△ADE中,∠AED=90°,
∴tan30°=DEAE,
即33=30AE,
∴AE=303,
∵AB=57,
∴BE=AB﹣AE=57﹣303,
∵四边形BCFE是矩形,
∴CF=BE=57﹣303.
在Rt△DCF中,∠DFC=90°,
∴∠CDF=∠DCF=45°.
∴DF=CF=57﹣303,
∴BC=EF=30﹣57+303=(303-27)米.
答:教学楼BC高约(303-27)米.
故答案为:(303-27)米.
13.
【解答】解:如图,作OC⊥AB于点C,
∴∠ACO=∠BCO=90°,
根据题意可知:
∠AOC=45°,∠BOC=30°,OC=12,
∴AC=OC=12,
∴BC=OC?tan30°=12×33=43.
∴AB=AC+BC=12+43(m).
所以旗杆AB的高度是(12+43)m.
故答案为:(12+43).
14.
【解答】解:根据题意可知:
∠ABC=90°,CD=10,
在Rt△ABC中,∠ACB=45°,
∴AB=CB,
在Rt△ABD中,∠ADB=30°,BD=CD+BC=10+AB,
∴tan30°=ABBD,
即33=AB10+AB,
解得AB≈13.7(米).
答:树高约为13.7米.
故答案为:13.7
15.
【解答】解:如图,作DE⊥AB于点E,
根据题意可知:
DC⊥BC,AB⊥BC,
∴四边形DCBE是矩形,
∴BE=DC=1.6,DE=CB=30,
∴在Rt△ADE中,∠ADE=30°,DE=30,
∴AE=DE?tan30°=30×33=103≈17(m).
答:教学楼的高度约为17m.
故答案为:17.
16.
【解答】解:如图所示:设无人机所在位置为点A,
根据题意可知:
∠BAD=60°,∠DAC=45°,BC=47(米),
设此时无人机距离地面的高度为x米,
则CD=x,则BD=47﹣x,AD=CD=x,
在Rt△ADB中,tan60°=BDAD,
即3=47-xx,
解得x=473-472(米).
答:此时无人机距离地面的高度为473-472米.
故答案为:473-472.
17.
【解答】解:在Rt△ABC中,∵∠CAB=90°,∠B=α,AC=800米,
∴tanα=ACAB,
∴AB=ACtanα=800tanα(米).
故答案为:800tanα.
18.
【解答】解:如图,过点B作BH⊥AE于点H,BF⊥CE于点F,
根据题意可知:
∠BAH=30°,
AB=AE=10,
∴BH=5,AH=53,
∵CE⊥AE,
∴四边形BHEF是矩形,
∴EF=BH=5,
BF=HE=AH+AE=53+10,
∵∠DAE=60°,
∴DE=AE?tan60°=103,
∴DF=DE﹣EF=103-5,
∵∠CBF=45°,
∴CF=BF=53+10,
∴CD=CF﹣DF=53+10﹣(103-5)=15﹣53(米).
所以标识牌CD的高度是(15﹣53)米.
故答案为:(15﹣53).
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.
【解答】解:(1)∵CD=2,tan∠CMD=13,
∴MD=6m;
(2)过点C作CE⊥AB于点E,
设BM=x,
∴BD=x+6,
∵∠AMB=60°,
∴∠BAM=30°,
∴AB=3x,
已知四边形CDBE是矩形,
∴BE=CD=2,CE=BD=x+6,
∴AE=3x﹣23
在Rt△ACE中,
∵tan30°=AECE,
∴13=3x-2x+6,
解得:x=3+3,
∴AB=3x=3+33≈8.2m.
20.
【解答】解:∵AB⊥BD,CD⊥BD,
∴四边形ABDE是矩形,
∴DE=AB=24m,
在Rt△AED中,AE=EDtanβ=243=83(m),
在Rt△ACE中,CE=AE?tanα=83×33=8(m),
∴CD=DE+CE=24+8=32(m).
答:乙楼CD的高为32m.
21.
【解答】解:在Rt△ADB中,
∵∠BDA=45°,
∴AD=AB=4m.
在Rt△ADC中,AC=AD?tan62°≈4×1.88=7.52(m).
∴BC=AC﹣AB=7.52﹣4=3.52≈3.5(m).
答:宣传牌BC的高度是3.5m.
22.
【解答】解:作DF⊥AB于F,
设AB=xm,
∵FB⊥EB,DE⊥EB,DF⊥AB,
∴四边形FBED为矩形,
∴FB=DE=10,DF=BE,
∴AF=10﹣x,
在Rt△AFD中,∠ADF=45°,
∴DF=AF=x﹣10,
在Rt△ABC中,∠ACB=53°,tan∠ACB=ABBC,
∴BC=ABtan∠ACB≈34x,
由题意得,BE﹣BC=CE,即x﹣10-34x=4,
解得,x=56,
答:钟楼AB的高度约为56m.
23.
【解答】解:∵∠MBN是△ABM的一个外角,
∴∠AMB=∠MBN﹣∠MAB=30°,
∴∠AMB=∠MAB,
∴BM=AB=50,
在Rt△MBN中,sin∠MBN=MNMB,
∴MN=BM?sin∠MBN=50×32=253≈43,
答:白塔的高度MN约为43米.
24.
【解答】解:设AC为xm,则CD=(x+120)m,
在Rt△ACB中,∠ABC=45°,
∴BC=AC=x,
∴CE=x+20,
在Rt△DCE中,tan∠DEC=CDCE,即x+120x+20≈1.346,
解得,x≈269.0,
∴CD=x+120=389.0≈389,
答:中原福塔CD的总高度约为389m.
