2.4二次函数的图象与性质(3)同步练习(含解析)
文档属性
| 名称 | 2.4二次函数的图象与性质(3)同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 16:45:13 | ||
图片预览




文档简介
2.4二次函数的图象与性质(3)
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,其中选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020春?岳麓区校级期末)将抛物线y=x2﹣4x﹣4向左平移3个单位,再向上平移3个单位,得到抛物线的表达式为( )
A.y=(x+1)2﹣13 B.y=(x﹣5)2﹣5
C.y=(x﹣5)2﹣13 D.y=(x+1)2﹣5
2.(2020?南岗区校级三模)对二次函数y=2(x﹣3)2﹣4的图象,下列叙述正确的是( )
A.顶点坐标为(﹣3,﹣4)
B.与y 轴的交点坐标为(0,﹣4)
C.当x≥3时,y随x增大而减小
D.最小值是y=﹣4
3.(2019秋?思明区校级期中)对于二次函数y=x2﹣2x+3的图象,下列说法正确的是( )
A.开口向下
B.对称轴是直线x=﹣1
C.当x<1时,y随x的增大而减小
D.函数最大值为4
4.(2019春?西湖区校级月考)二次函数y=a2x2+bx+c(a≠0)的图象的顶点为P(m,k)且有一点Q(k,m)也在该函数图象上,则下列结论一定正确的是( )
A.m=k B.m>k C.m≥k D.m<k
5.(2020?宝应县一模)二次函数y=x2﹣ax+b的图象如图所示,对称轴为直线x=1,下列结论不正确的是( )
A.a=2
B.顶点的坐标为(1,﹣4)
C.当﹣1<x<3时,y>0
D.当x>3时,y 随着x的增大而增大
6.(2019?温岭市一模)将抛物线y=x2﹣2x﹣3沿x轴折得到的新抛物线的解析式为( )
A.y=﹣x2+2x+3 B.y=﹣x2﹣2x﹣3 C.y=x2+2x﹣3 D.y=x2﹣2x+3
7.(2019秋?工业园区期末)下列对于二次函数y=﹣x2+x图象的描述中,正确的是( )
A.开口向上
B.对称轴是y轴
C.有最低点
D.在对称轴右侧的部分从左往右是下降的
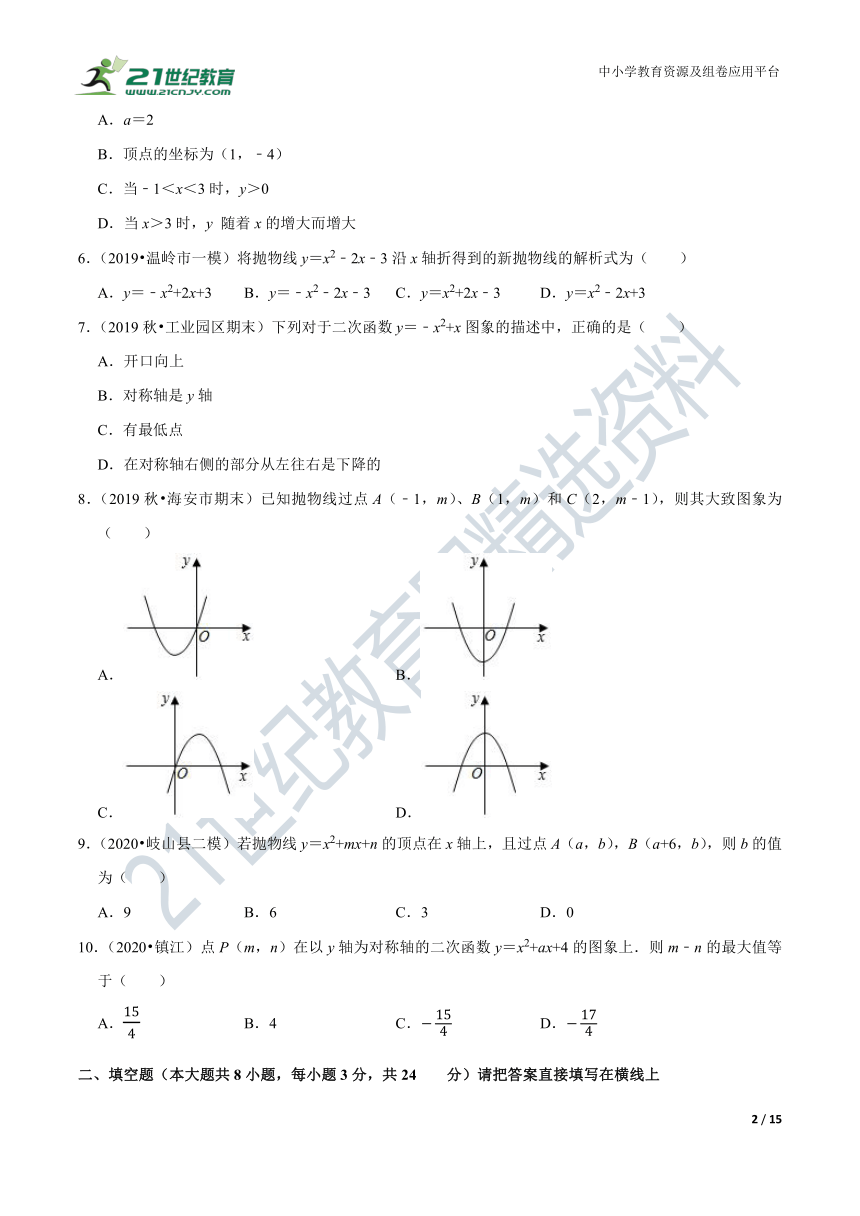
8.(2019秋?海安市期末)已知抛物线过点A(﹣1,m)、B(1,m)和C(2,m﹣1),则其大致图象为( )
A. B.
C. D.
9.(2020?岐山县二模)若抛物线y=x2+mx+n的顶点在x轴上,且过点A(a,b),B(a+6,b),则b的值为( )
A.9 B.6 C.3 D.0
10.(2020?镇江)点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上.则m﹣n的最大值等于( )
A.154 B.4 C.-154 D.-174
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020?立山区二模)若二次函数y=mx2+(m﹣2)x+m的顶点在x轴上,则m= .
12.(2020?海珠区一模)抛物线y=x2+bx+c经过点A(﹣2,0)、B(1,0)两点,则该抛物线的顶点坐标是 .
13.(2018秋?顺庆区校级月考)某同学用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格由于粗心他算错了其中一个y的值,则这个错误的数值是 .
x
…
﹣2
﹣1
0
1
2
…
y
…
﹣11
﹣2
1
﹣2
﹣5
…
14.(2020?梁园区一模)点P1(﹣2,y1),P2(0,y2),P3(1,y3)均在二次函数y=﹣x2﹣2x+c 的图象上,则 y1,y2,y3的大小关系是 .
15.(2020?仓山区校级模拟)若抛物线y=ax2+bx+c的开口向上,对称轴是直线x=12,点A(﹣2,y1)、B (1,y2)、C(2,y3)都在该抛物线上,则y1、y2、y3的大小关系是 .
16.(2019秋?南充期末)将抛物线y=﹣x2﹣4x(﹣4≤x≤0)沿y轴折叠后得另一条抛物线,若直线y=x+b与这两条抛物线共有3个公共点,则b的取值范围为 .
17.(2020春?崇川区期末)抛物线y=x2+bx+c经过点A(﹣2,m),B(4,m),C(5,n)给出下列结论:①b=2;②函数最小值为c﹣1;③当x=2时,y=c;④c>n.其中正确的有 .(填序号)
18.(2020?长春一模)如图,直线y=x+1与抛物线y=x2﹣4x+5交于A,B两点,点P是y轴上的一个动点,当△PAB的周长最小时,点P的坐标为 .
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020秋?江岸区校级月考)已知二次函数C2:y=ax2+2x+c图象经过点A(2,3)和点C(0,3).
(1)求该二次函数的解析式;
(2)填空:抛物线C1:y=ax2的顶点坐标为( , ),而抛物线C2:y=ax2+2x+c的顶点坐标为( , ).将抛物线C1经过适当平移,得到抛物线C2:应该先向 (填:左或右)平移 个单位长度,再向 (填:上或下)平移 个单位长度.
20.设抛物线为y=x2﹣kx+k﹣1,根据下列各条件,求k的值.
(1)抛物线的顶点在x轴上;
(2)抛物线的顶点在y轴上;
(3)抛物线的顶点(﹣1,﹣4);
(4)抛物线经过原点;
(5)当x=1时,y有最小值;
(6)y的最小值为﹣1.
21.(2020?海门市一模)已知平面直角坐标系xOy中,抛物线y═12x2﹣mx+12m2+m.
(1)若该抛物线经过原点,求m的值;
(2)求证该抛物线的顶点在直线y=x上;
(3)若点A(﹣4,0),B(0,2),当该抛物线与线段AB只有一个公共点时,结合函数图象,直接写出m的取值范围.
22.(2020?建水县模拟)如图所示,已知抛物线y=13x2+bx+c经过点A(﹣1,0),B(5,0).
(1)求抛物线的解析式并写出顶点M的坐标;
(2)若点C在抛物线上,且点C的横坐标为8,求四边形AMBC的面积.
23.(2020秋?津南区期中)二次函数y=ax2+bx+c(a≠0)的自变量x与对应的函数y的值(部分)如表所示:
x
……
﹣3
﹣2
﹣1
0
1
2
……
y
……
m
7
1
﹣1
1
7
……
解答下列问题:
(Ⅰ)求这个二次函数的解析式;
(Ⅱ)表格中m的值等于 ;
(Ⅲ)在直角坐标系中,画出这个函数的图象;
(Ⅳ)将这个函数的图象向右平移2个单位长,向上平移1个单位长,写出平移后的二次函数解析式.
24.(2020?湖北)把抛物线C1:y=x2+2x+3先向右平移4个单位长度,再向下平移5个单位长度得到抛物线C2.
(1)直接写出抛物线C2的函数关系式;
(2)动点P(a,﹣6)能否在抛物线C2上?请说明理由;
(3)若点A(m,y1),B(n,y2)都在抛物线C2上,且m<n<0,比较y1,y2的大小,并说明理由.
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解答】解:∵y=x2﹣4x﹣4=(x﹣2)2﹣8,
∴将抛物线y=x2﹣4x﹣4向左平移3个单位,再向上平移3个单位,得到抛物线的表达式为y=(x﹣2+3)2﹣8+3,即y=(x+1)2﹣5.
故选:D.
2.【解答】解:由二次函数y=2(x﹣3)2﹣4可知,开口向上.对称轴为直线x=3,顶点坐标为(3,﹣4),抛物线有最小值﹣4,当x≥3时,y随x增大而增大,故A、C错误,D正确;
令x=0,则y=14,抛物线与y轴的交点为(0,14),故B错误;
故选:D.
3.【解答】解:∵y=x2﹣2x+3=(x﹣1)2+2,
∴由a=1>0知抛物线开口向上,顶点坐标是(1,2),对称轴是直线x=1,当x<1时,y随x的增大而减小,函数有最小值为2,无最大值,
∴C选项正确;
故选:C.
4.【解答】解:∵二次函数y=a2x2+bx+c(a≠0),
∴a2>0,
∴该函数开口向上,函数有最小值,
∵二次函数y=a2x2+bx+c(a≠0)的图象的顶点为P(m,k)且有一点Q(k,m)也在该函数图象上,
∴m≥k,
故选:C.
5.【解答】解:∵二次函数y=x2﹣ax+b对称轴为直线x=1,
∴--a2×1=1,得a=2,故选项A正确;
∵该函数图象过点(﹣1,0),
∴0=1﹣2×(﹣1)+b,得b=﹣3,
∴y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴该抛物线的顶点坐标为(1,﹣4),故选项B正确;
∵二次函数y=x2﹣ax+b对称轴为直线x=1,过点(﹣1,0),
∴该函数过点(3,0),
∴当﹣1<x<3时,y<0,故选项C不正确;
∴当x>1时,y随x的增大而增大,故选项D正确;
故选:C.
6.【解答】解:将抛物线y=x2﹣2x﹣3沿x轴折得到的新抛物线的解析式为:﹣y=x2﹣2x﹣3,即y=﹣x2+2x+3.
故选:A.
7.【解答】解:∵二次函数y=﹣x2+x=﹣(x-12)2+14,
∴a=﹣1,该函数的图象开口向下,故选项A错误;
对称轴是直线x=12,故选项B错误;
当x=12时取得最大值14,该函数有最高点,故选项C错误;
在对称轴右侧的部分从左往右是下降的,故选项D正确;
故选:D.
8.【解答】解:∵抛物线过点A(﹣1,m)、B(1,m),
∴抛物线的对称轴为y轴,
∴可排除A、C.
∵1<2,m>m﹣1,
∴在y轴右侧y随x的增大而减小,
∴抛物线开口向下,
∴B错误,D正确.
故选:D.
9.【解答】解:法一:∵抛物线y=x2+mx+n顶点在x轴上,
∴△=m2﹣4×1×n=m2﹣4n=0,
∴n=14m2,
∵抛物线y=x2+mx+n过点A(a,b),B(a+6,b),
∴b=a2+ma+n,b=(a+6)2+m(a+6)+n,
∴a2+ma+n=(a+6)2+m(a+6)+n,
化简,得
a=-6-m2,
∴b=a2+ma+n=(-6-m2)2+m×-6-m2+14m2=9,
法二:∵抛物线y=x2+mx+n过点A(a,b),B(a+6,b),
∴对称轴是x=a+a+62=a+3,
∵抛物线y=x2+mx+n顶点在x轴上,
∴y=x2+mx+n=[x﹣(a+3)]2,
把(a+6,b)代入得:b=[(a+6)﹣(a+3)]2=32=9,
故选:A.
10.【解答】解:∵点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上,
∴a=0,
∴n=m2+4,
∴m﹣n=m﹣(m2+4)=﹣m2+m﹣4=﹣(m-12)2-154,
∴当m=12时,m﹣n取得最大值,此时m﹣n=-154,
故选:C.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解答】解:∵二次函数y=mx2+(m﹣2)x+m的顶点在x轴上,
∴4m?m-(m-2)24m=0,
解得m=﹣2或23.
故答案为:﹣2或23.
12.【解答】解:∵抛物线y=x2+bx+c经过点A(﹣2,0)、B(1,0)两点,
∴4-2b+c=01+b+c=0,
解得:b=1c=-2,
∴y=x2+x﹣2=(x+12)2-94,
∴顶点坐标为(-12,-94),
故答案为:(-12,-94).
13.【解答】解:由函数图象关于对称轴对称,得
(﹣1,﹣2),(0,1),(1,﹣2)在函数图象上,
把(﹣1,﹣2),(0,1),(1,﹣2)代入函数解析式,得
a-b+c=-2c=1a+b+c=-2,
解得a=-3b=0c=1,
函数解析式为y=﹣3x2+1
x=2时y=﹣11,
故这个错误的数值是﹣5,
故答案为﹣5.
14.【解答】解:二次函数y=﹣x2﹣2x+c 的二次项系数a=﹣1,
∴函数图象开口向下
又∵对称轴为x=﹣1,
∴y1=y2>y3
点故答案为:y1=y2>y3.
15.【解答】解:抛物线y=ax2+bx+c的开口向上,对称轴是直线x=12,当x>12时,y随x的增大而增大,
∵点A(﹣2,y1)、B(1,y2)、C(2,y3)都在该抛物线上,
∴点A关于对称轴x=12的对称点是(3,y1),
∴y2<y3<y1,
故答案为y2<y3<y1.
16.【解答】解:将抛物线y=﹣x2﹣4x(﹣4≤x≤0)沿y轴折叠后得另一条抛物线为y=﹣x2+4x(0≤x≤4)
画出函数如图,
由图象可知,
当直线y=x+b经过原点时有两个公共点,此时b=0,
解y=x+by=-x2+4x,整理得x2﹣3x+b=0,
若直线y=x+b与这两条抛物线共有3个公共点,
则△=9﹣4b>0,
解得b<94
所以,当0<b<94时,直线y=x+b与这两条抛物线共有3个公共点,
故答案为0<b<94.
17.【解答】解:∵二次函数y=x2+bx+c的图象经过点A(﹣2,m)、B(4,m),
∴-b2=-2+42=1,
∴b=﹣2,故①错误;
∴y=x2﹣2x+c,
把x=1代入得,y=c﹣1,
∴函数最小值为c﹣1,故②正确;
把x=2代入得,y=4﹣4+c=c,故③正确;
∵点C(5,n)在二次函数y=x2﹣2x+c的图象上,
∴n=25﹣10+c,
∴n﹣c=15,
∴c<n,故④错误;
故答案为②③.
18.【解答】解:y=x+1y=x2-4x+5,
解得,x=1y=2或x=4y=5,
∴点A的坐标为(1,2),点B的坐标为(4,5),
∴AB=(5-2)2+(4-1)2=32,
作点A关于y轴的对称点A′,连接A′B与y轴的交于P,则此时△PAB的周长最小,
点A′的坐标为(﹣1,2),点B的坐标为(4,5),
设直线A′B的函数解析式为y=kx+b,
-k+b=24k+b=5,得k=35b=135,
∴直线A′B的函数解析式为y=35x+135,
当x=0时,y=135,
即点P的坐标为(0,135),
故答案为:(0,135).
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解答】解:(1)将点A和点C的坐标代入函数解析式,得4a+4+c=3c=3,
解得a=-1c=3,
二次函数的解析式为y=﹣x2+2x+3;
(2)∵抛物线C2:y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴抛物线C1:y=﹣x2的顶点坐标为(0,0),而抛物线C2:y=ax2+2x+c的顶点坐标为(1,4).将抛物线C1经过适当平移,得到抛物线C2:应该先向右(填:左或右)平移1个单位长度,再向上(填:上或下)平移4个单位长度.
故答案为:0、0,1、4,右,1,上,4.
20.【解答】解:(1)抛物线的顶点在x轴上,即4(k-1)-k24=0,∴k=2;
(2)抛物线的顶点在y轴上,即x=--k2=0,∴k=0;
(3)抛物线的顶点(﹣1,﹣4),即x=--k2=-1,4(k-1)-k24=-4,∴k=1;
(4)抛物线经过原点,即k﹣1=0,∴k=1;
(5)当x=1时,y有最小值,即--k2=1,k=2;
(6)y的最小值为﹣1,y=(x-k2)2+k﹣1-k24,即k﹣1-k24=-1,解得:k=0或k=4.
21.【解答】解:(1)∵抛物线经过原点,
∴12m2+m=0,
解得m1=0,m2=﹣2;
(2)∵y═12x2﹣mx+12m2+m
=12(x﹣m)2+m,
∴该抛物线的顶点坐标为(m,m),
∴抛物线的顶点直线直线y=x上;
(3)设直线AB的解析式为y=kx+b,
把点A(﹣4,0),B(0,2)代入得-4k+b=0b=2,解得k=12b=2,
∴直线AB的解析式为y=12x+2,
令12x+2=12x2﹣mx+12m2+m,整理得12x2﹣(m+12)x+12m2+m﹣2=0,
△=(m+12)2﹣4×12(12m2+m﹣2)=0,
解得m=174,
∵此时对称轴为x=-1742×12=174>0,故舍去;
把A(﹣4,0)代入y=12x2﹣mx+12m2+m得,
12m2+5m+8=0,
解得m=﹣2或﹣8;
把B(0,2)代入y=12x2﹣mx+12m2+m得,
12m2+m+﹣2=0,
解得m=﹣1±5,
由图象可知,该抛物线与线段AB只有一个公共点时,﹣8≤m≤﹣1-5或﹣2≤m≤﹣1+5.
22.【解答】解:(1)∵抛物线y=13x2+bx+c经过点A(﹣1,0),B(5,0).
∴函数的表达式为:y=13(x+1)(x﹣5)=13(x2﹣4x﹣5)=13x2-43x-53,
点M坐标为(2,﹣3);
(2)当x=8时,y=13(x+1)(x﹣5)=9,即点C(8,9),
因为AB=5+1=6,
且△ABM、△ABC的高分别是点M、点C纵坐标的绝对值,
所以S四边形AMBC=S△ABM+S△ABC=6×|-3|2+6×|9|2=36.
23.【解答】解:(Ⅰ)由表格可知,
该函数有最小值,当x=0时,y=﹣1,当x=﹣1和x=1时的函数值相等,
即该二次函数图象的开口方向向上,对称轴是直线x=0,顶点坐标为(0,﹣1),
设二次函数为y=ax2﹣1,把x=1,y=1代入得,1=a﹣1,解得a=2,
∴二次函数的解析式为y=2x2﹣1;
(Ⅱ)把x=﹣3代入y=2x2﹣1得,y=17;
∴m=17,
故答案为17;
(Ⅲ)在直角坐标系中,画出这个函数的图象如图:
(Ⅳ)将这个函数的图象向右平移2个单位长,向上平移1个单位长,则平移后的二次函数解析式为y=2(x﹣2)2.
24.【解答】解:(1)∵y=x2+2x+3=(x+1)2+2,
∴把抛物线C1:y=x2+2x+3先向右平移4个单位长度,再向下平移5个单位长度得到抛物线C2:y=(x+1﹣4)2+2﹣5,即y=(x﹣3)2﹣3,
∴抛物线C2的函数关系式为:y=(x﹣3)2﹣3.
(2)动点P(a,﹣6)不在抛物线C2上,理由如下:
∵抛物线C2的函数关系式为:y=(x﹣3)2﹣3,
∴函数的最小值为﹣3,
∵﹣6<﹣3,
∴动点P(a,﹣6)不在抛物线C2上;
(3)∵抛物线C2的函数关系式为:y=(x﹣3)2﹣3,
∴抛物线的开口向上,对称轴为x=3,
∴当x<3时,y随x的增大而减小,
∵点A(m,y1),B(n,y2)都在抛物线C2上,且m<n<0<3,
∴y1>y2.
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,其中选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020春?岳麓区校级期末)将抛物线y=x2﹣4x﹣4向左平移3个单位,再向上平移3个单位,得到抛物线的表达式为( )
A.y=(x+1)2﹣13 B.y=(x﹣5)2﹣5
C.y=(x﹣5)2﹣13 D.y=(x+1)2﹣5
2.(2020?南岗区校级三模)对二次函数y=2(x﹣3)2﹣4的图象,下列叙述正确的是( )
A.顶点坐标为(﹣3,﹣4)
B.与y 轴的交点坐标为(0,﹣4)
C.当x≥3时,y随x增大而减小
D.最小值是y=﹣4
3.(2019秋?思明区校级期中)对于二次函数y=x2﹣2x+3的图象,下列说法正确的是( )
A.开口向下
B.对称轴是直线x=﹣1
C.当x<1时,y随x的增大而减小
D.函数最大值为4
4.(2019春?西湖区校级月考)二次函数y=a2x2+bx+c(a≠0)的图象的顶点为P(m,k)且有一点Q(k,m)也在该函数图象上,则下列结论一定正确的是( )
A.m=k B.m>k C.m≥k D.m<k
5.(2020?宝应县一模)二次函数y=x2﹣ax+b的图象如图所示,对称轴为直线x=1,下列结论不正确的是( )
A.a=2
B.顶点的坐标为(1,﹣4)
C.当﹣1<x<3时,y>0
D.当x>3时,y 随着x的增大而增大
6.(2019?温岭市一模)将抛物线y=x2﹣2x﹣3沿x轴折得到的新抛物线的解析式为( )
A.y=﹣x2+2x+3 B.y=﹣x2﹣2x﹣3 C.y=x2+2x﹣3 D.y=x2﹣2x+3
7.(2019秋?工业园区期末)下列对于二次函数y=﹣x2+x图象的描述中,正确的是( )
A.开口向上
B.对称轴是y轴
C.有最低点
D.在对称轴右侧的部分从左往右是下降的
8.(2019秋?海安市期末)已知抛物线过点A(﹣1,m)、B(1,m)和C(2,m﹣1),则其大致图象为( )
A. B.
C. D.
9.(2020?岐山县二模)若抛物线y=x2+mx+n的顶点在x轴上,且过点A(a,b),B(a+6,b),则b的值为( )
A.9 B.6 C.3 D.0
10.(2020?镇江)点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上.则m﹣n的最大值等于( )
A.154 B.4 C.-154 D.-174
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020?立山区二模)若二次函数y=mx2+(m﹣2)x+m的顶点在x轴上,则m= .
12.(2020?海珠区一模)抛物线y=x2+bx+c经过点A(﹣2,0)、B(1,0)两点,则该抛物线的顶点坐标是 .
13.(2018秋?顺庆区校级月考)某同学用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格由于粗心他算错了其中一个y的值,则这个错误的数值是 .
x
…
﹣2
﹣1
0
1
2
…
y
…
﹣11
﹣2
1
﹣2
﹣5
…
14.(2020?梁园区一模)点P1(﹣2,y1),P2(0,y2),P3(1,y3)均在二次函数y=﹣x2﹣2x+c 的图象上,则 y1,y2,y3的大小关系是 .
15.(2020?仓山区校级模拟)若抛物线y=ax2+bx+c的开口向上,对称轴是直线x=12,点A(﹣2,y1)、B (1,y2)、C(2,y3)都在该抛物线上,则y1、y2、y3的大小关系是 .
16.(2019秋?南充期末)将抛物线y=﹣x2﹣4x(﹣4≤x≤0)沿y轴折叠后得另一条抛物线,若直线y=x+b与这两条抛物线共有3个公共点,则b的取值范围为 .
17.(2020春?崇川区期末)抛物线y=x2+bx+c经过点A(﹣2,m),B(4,m),C(5,n)给出下列结论:①b=2;②函数最小值为c﹣1;③当x=2时,y=c;④c>n.其中正确的有 .(填序号)
18.(2020?长春一模)如图,直线y=x+1与抛物线y=x2﹣4x+5交于A,B两点,点P是y轴上的一个动点,当△PAB的周长最小时,点P的坐标为 .
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020秋?江岸区校级月考)已知二次函数C2:y=ax2+2x+c图象经过点A(2,3)和点C(0,3).
(1)求该二次函数的解析式;
(2)填空:抛物线C1:y=ax2的顶点坐标为( , ),而抛物线C2:y=ax2+2x+c的顶点坐标为( , ).将抛物线C1经过适当平移,得到抛物线C2:应该先向 (填:左或右)平移 个单位长度,再向 (填:上或下)平移 个单位长度.
20.设抛物线为y=x2﹣kx+k﹣1,根据下列各条件,求k的值.
(1)抛物线的顶点在x轴上;
(2)抛物线的顶点在y轴上;
(3)抛物线的顶点(﹣1,﹣4);
(4)抛物线经过原点;
(5)当x=1时,y有最小值;
(6)y的最小值为﹣1.
21.(2020?海门市一模)已知平面直角坐标系xOy中,抛物线y═12x2﹣mx+12m2+m.
(1)若该抛物线经过原点,求m的值;
(2)求证该抛物线的顶点在直线y=x上;
(3)若点A(﹣4,0),B(0,2),当该抛物线与线段AB只有一个公共点时,结合函数图象,直接写出m的取值范围.
22.(2020?建水县模拟)如图所示,已知抛物线y=13x2+bx+c经过点A(﹣1,0),B(5,0).
(1)求抛物线的解析式并写出顶点M的坐标;
(2)若点C在抛物线上,且点C的横坐标为8,求四边形AMBC的面积.
23.(2020秋?津南区期中)二次函数y=ax2+bx+c(a≠0)的自变量x与对应的函数y的值(部分)如表所示:
x
……
﹣3
﹣2
﹣1
0
1
2
……
y
……
m
7
1
﹣1
1
7
……
解答下列问题:
(Ⅰ)求这个二次函数的解析式;
(Ⅱ)表格中m的值等于 ;
(Ⅲ)在直角坐标系中,画出这个函数的图象;
(Ⅳ)将这个函数的图象向右平移2个单位长,向上平移1个单位长,写出平移后的二次函数解析式.
24.(2020?湖北)把抛物线C1:y=x2+2x+3先向右平移4个单位长度,再向下平移5个单位长度得到抛物线C2.
(1)直接写出抛物线C2的函数关系式;
(2)动点P(a,﹣6)能否在抛物线C2上?请说明理由;
(3)若点A(m,y1),B(n,y2)都在抛物线C2上,且m<n<0,比较y1,y2的大小,并说明理由.
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解答】解:∵y=x2﹣4x﹣4=(x﹣2)2﹣8,
∴将抛物线y=x2﹣4x﹣4向左平移3个单位,再向上平移3个单位,得到抛物线的表达式为y=(x﹣2+3)2﹣8+3,即y=(x+1)2﹣5.
故选:D.
2.【解答】解:由二次函数y=2(x﹣3)2﹣4可知,开口向上.对称轴为直线x=3,顶点坐标为(3,﹣4),抛物线有最小值﹣4,当x≥3时,y随x增大而增大,故A、C错误,D正确;
令x=0,则y=14,抛物线与y轴的交点为(0,14),故B错误;
故选:D.
3.【解答】解:∵y=x2﹣2x+3=(x﹣1)2+2,
∴由a=1>0知抛物线开口向上,顶点坐标是(1,2),对称轴是直线x=1,当x<1时,y随x的增大而减小,函数有最小值为2,无最大值,
∴C选项正确;
故选:C.
4.【解答】解:∵二次函数y=a2x2+bx+c(a≠0),
∴a2>0,
∴该函数开口向上,函数有最小值,
∵二次函数y=a2x2+bx+c(a≠0)的图象的顶点为P(m,k)且有一点Q(k,m)也在该函数图象上,
∴m≥k,
故选:C.
5.【解答】解:∵二次函数y=x2﹣ax+b对称轴为直线x=1,
∴--a2×1=1,得a=2,故选项A正确;
∵该函数图象过点(﹣1,0),
∴0=1﹣2×(﹣1)+b,得b=﹣3,
∴y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴该抛物线的顶点坐标为(1,﹣4),故选项B正确;
∵二次函数y=x2﹣ax+b对称轴为直线x=1,过点(﹣1,0),
∴该函数过点(3,0),
∴当﹣1<x<3时,y<0,故选项C不正确;
∴当x>1时,y随x的增大而增大,故选项D正确;
故选:C.
6.【解答】解:将抛物线y=x2﹣2x﹣3沿x轴折得到的新抛物线的解析式为:﹣y=x2﹣2x﹣3,即y=﹣x2+2x+3.
故选:A.
7.【解答】解:∵二次函数y=﹣x2+x=﹣(x-12)2+14,
∴a=﹣1,该函数的图象开口向下,故选项A错误;
对称轴是直线x=12,故选项B错误;
当x=12时取得最大值14,该函数有最高点,故选项C错误;
在对称轴右侧的部分从左往右是下降的,故选项D正确;
故选:D.
8.【解答】解:∵抛物线过点A(﹣1,m)、B(1,m),
∴抛物线的对称轴为y轴,
∴可排除A、C.
∵1<2,m>m﹣1,
∴在y轴右侧y随x的增大而减小,
∴抛物线开口向下,
∴B错误,D正确.
故选:D.
9.【解答】解:法一:∵抛物线y=x2+mx+n顶点在x轴上,
∴△=m2﹣4×1×n=m2﹣4n=0,
∴n=14m2,
∵抛物线y=x2+mx+n过点A(a,b),B(a+6,b),
∴b=a2+ma+n,b=(a+6)2+m(a+6)+n,
∴a2+ma+n=(a+6)2+m(a+6)+n,
化简,得
a=-6-m2,
∴b=a2+ma+n=(-6-m2)2+m×-6-m2+14m2=9,
法二:∵抛物线y=x2+mx+n过点A(a,b),B(a+6,b),
∴对称轴是x=a+a+62=a+3,
∵抛物线y=x2+mx+n顶点在x轴上,
∴y=x2+mx+n=[x﹣(a+3)]2,
把(a+6,b)代入得:b=[(a+6)﹣(a+3)]2=32=9,
故选:A.
10.【解答】解:∵点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上,
∴a=0,
∴n=m2+4,
∴m﹣n=m﹣(m2+4)=﹣m2+m﹣4=﹣(m-12)2-154,
∴当m=12时,m﹣n取得最大值,此时m﹣n=-154,
故选:C.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解答】解:∵二次函数y=mx2+(m﹣2)x+m的顶点在x轴上,
∴4m?m-(m-2)24m=0,
解得m=﹣2或23.
故答案为:﹣2或23.
12.【解答】解:∵抛物线y=x2+bx+c经过点A(﹣2,0)、B(1,0)两点,
∴4-2b+c=01+b+c=0,
解得:b=1c=-2,
∴y=x2+x﹣2=(x+12)2-94,
∴顶点坐标为(-12,-94),
故答案为:(-12,-94).
13.【解答】解:由函数图象关于对称轴对称,得
(﹣1,﹣2),(0,1),(1,﹣2)在函数图象上,
把(﹣1,﹣2),(0,1),(1,﹣2)代入函数解析式,得
a-b+c=-2c=1a+b+c=-2,
解得a=-3b=0c=1,
函数解析式为y=﹣3x2+1
x=2时y=﹣11,
故这个错误的数值是﹣5,
故答案为﹣5.
14.【解答】解:二次函数y=﹣x2﹣2x+c 的二次项系数a=﹣1,
∴函数图象开口向下
又∵对称轴为x=﹣1,
∴y1=y2>y3
点故答案为:y1=y2>y3.
15.【解答】解:抛物线y=ax2+bx+c的开口向上,对称轴是直线x=12,当x>12时,y随x的增大而增大,
∵点A(﹣2,y1)、B(1,y2)、C(2,y3)都在该抛物线上,
∴点A关于对称轴x=12的对称点是(3,y1),
∴y2<y3<y1,
故答案为y2<y3<y1.
16.【解答】解:将抛物线y=﹣x2﹣4x(﹣4≤x≤0)沿y轴折叠后得另一条抛物线为y=﹣x2+4x(0≤x≤4)
画出函数如图,
由图象可知,
当直线y=x+b经过原点时有两个公共点,此时b=0,
解y=x+by=-x2+4x,整理得x2﹣3x+b=0,
若直线y=x+b与这两条抛物线共有3个公共点,
则△=9﹣4b>0,
解得b<94
所以,当0<b<94时,直线y=x+b与这两条抛物线共有3个公共点,
故答案为0<b<94.
17.【解答】解:∵二次函数y=x2+bx+c的图象经过点A(﹣2,m)、B(4,m),
∴-b2=-2+42=1,
∴b=﹣2,故①错误;
∴y=x2﹣2x+c,
把x=1代入得,y=c﹣1,
∴函数最小值为c﹣1,故②正确;
把x=2代入得,y=4﹣4+c=c,故③正确;
∵点C(5,n)在二次函数y=x2﹣2x+c的图象上,
∴n=25﹣10+c,
∴n﹣c=15,
∴c<n,故④错误;
故答案为②③.
18.【解答】解:y=x+1y=x2-4x+5,
解得,x=1y=2或x=4y=5,
∴点A的坐标为(1,2),点B的坐标为(4,5),
∴AB=(5-2)2+(4-1)2=32,
作点A关于y轴的对称点A′,连接A′B与y轴的交于P,则此时△PAB的周长最小,
点A′的坐标为(﹣1,2),点B的坐标为(4,5),
设直线A′B的函数解析式为y=kx+b,
-k+b=24k+b=5,得k=35b=135,
∴直线A′B的函数解析式为y=35x+135,
当x=0时,y=135,
即点P的坐标为(0,135),
故答案为:(0,135).
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解答】解:(1)将点A和点C的坐标代入函数解析式,得4a+4+c=3c=3,
解得a=-1c=3,
二次函数的解析式为y=﹣x2+2x+3;
(2)∵抛物线C2:y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴抛物线C1:y=﹣x2的顶点坐标为(0,0),而抛物线C2:y=ax2+2x+c的顶点坐标为(1,4).将抛物线C1经过适当平移,得到抛物线C2:应该先向右(填:左或右)平移1个单位长度,再向上(填:上或下)平移4个单位长度.
故答案为:0、0,1、4,右,1,上,4.
20.【解答】解:(1)抛物线的顶点在x轴上,即4(k-1)-k24=0,∴k=2;
(2)抛物线的顶点在y轴上,即x=--k2=0,∴k=0;
(3)抛物线的顶点(﹣1,﹣4),即x=--k2=-1,4(k-1)-k24=-4,∴k=1;
(4)抛物线经过原点,即k﹣1=0,∴k=1;
(5)当x=1时,y有最小值,即--k2=1,k=2;
(6)y的最小值为﹣1,y=(x-k2)2+k﹣1-k24,即k﹣1-k24=-1,解得:k=0或k=4.
21.【解答】解:(1)∵抛物线经过原点,
∴12m2+m=0,
解得m1=0,m2=﹣2;
(2)∵y═12x2﹣mx+12m2+m
=12(x﹣m)2+m,
∴该抛物线的顶点坐标为(m,m),
∴抛物线的顶点直线直线y=x上;
(3)设直线AB的解析式为y=kx+b,
把点A(﹣4,0),B(0,2)代入得-4k+b=0b=2,解得k=12b=2,
∴直线AB的解析式为y=12x+2,
令12x+2=12x2﹣mx+12m2+m,整理得12x2﹣(m+12)x+12m2+m﹣2=0,
△=(m+12)2﹣4×12(12m2+m﹣2)=0,
解得m=174,
∵此时对称轴为x=-1742×12=174>0,故舍去;
把A(﹣4,0)代入y=12x2﹣mx+12m2+m得,
12m2+5m+8=0,
解得m=﹣2或﹣8;
把B(0,2)代入y=12x2﹣mx+12m2+m得,
12m2+m+﹣2=0,
解得m=﹣1±5,
由图象可知,该抛物线与线段AB只有一个公共点时,﹣8≤m≤﹣1-5或﹣2≤m≤﹣1+5.
22.【解答】解:(1)∵抛物线y=13x2+bx+c经过点A(﹣1,0),B(5,0).
∴函数的表达式为:y=13(x+1)(x﹣5)=13(x2﹣4x﹣5)=13x2-43x-53,
点M坐标为(2,﹣3);
(2)当x=8时,y=13(x+1)(x﹣5)=9,即点C(8,9),
因为AB=5+1=6,
且△ABM、△ABC的高分别是点M、点C纵坐标的绝对值,
所以S四边形AMBC=S△ABM+S△ABC=6×|-3|2+6×|9|2=36.
23.【解答】解:(Ⅰ)由表格可知,
该函数有最小值,当x=0时,y=﹣1,当x=﹣1和x=1时的函数值相等,
即该二次函数图象的开口方向向上,对称轴是直线x=0,顶点坐标为(0,﹣1),
设二次函数为y=ax2﹣1,把x=1,y=1代入得,1=a﹣1,解得a=2,
∴二次函数的解析式为y=2x2﹣1;
(Ⅱ)把x=﹣3代入y=2x2﹣1得,y=17;
∴m=17,
故答案为17;
(Ⅲ)在直角坐标系中,画出这个函数的图象如图:
(Ⅳ)将这个函数的图象向右平移2个单位长,向上平移1个单位长,则平移后的二次函数解析式为y=2(x﹣2)2.
24.【解答】解:(1)∵y=x2+2x+3=(x+1)2+2,
∴把抛物线C1:y=x2+2x+3先向右平移4个单位长度,再向下平移5个单位长度得到抛物线C2:y=(x+1﹣4)2+2﹣5,即y=(x﹣3)2﹣3,
∴抛物线C2的函数关系式为:y=(x﹣3)2﹣3.
(2)动点P(a,﹣6)不在抛物线C2上,理由如下:
∵抛物线C2的函数关系式为:y=(x﹣3)2﹣3,
∴函数的最小值为﹣3,
∵﹣6<﹣3,
∴动点P(a,﹣6)不在抛物线C2上;
(3)∵抛物线C2的函数关系式为:y=(x﹣3)2﹣3,
∴抛物线的开口向上,对称轴为x=3,
∴当x<3时,y随x的增大而减小,
∵点A(m,y1),B(n,y2)都在抛物线C2上,且m<n<0<3,
∴y1>y2.
