【课时作业】3.5确定圆的条件(含答案)
文档属性
| 名称 | 【课时作业】3.5确定圆的条件(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 266.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 16:48:06 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2020-2021学年九年级数学下册课时作业(北师版)
第三章 圆
5 确定圆的条件
一、选择题
1.只能作一个圆的条件是( )
A.已知圆心 B.同一直线上的三点
C.已知半径 D.过不在同一直线上的三点
2.△ABC的外接圆的圆心在△ABC的外部,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.无法确定
3.下列说法正确的是( )
A.三角形的外心在三角形外
B.任意一个圆,有且只有一个内接三角形
C.任意一个三角形一定有一个外接圆,并且只有一个外接圆
D.三角形的外心是三边上的高的交点
4.小颖同学在手工制作中,把一个边长为12cm的等边三角形纸片贴到一个圆的纸片上,若三角形的三个顶点,恰好都在这个圆上,则圆的半径为( )
A.2cm B.4cm C.6cm D.8cm
5.小亮不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( )
A.第①块 B.第②块 C.第③块 D.第④块
6.在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,则它的外心与顶点C的距离为( )
A.3cm B.4cm C.5cm D.2.5cm
7.已知AB=5cm,则经过A,B两点,且半径为3cm的圆有( )
A.0个 B.1个 C.2个 D.无数个
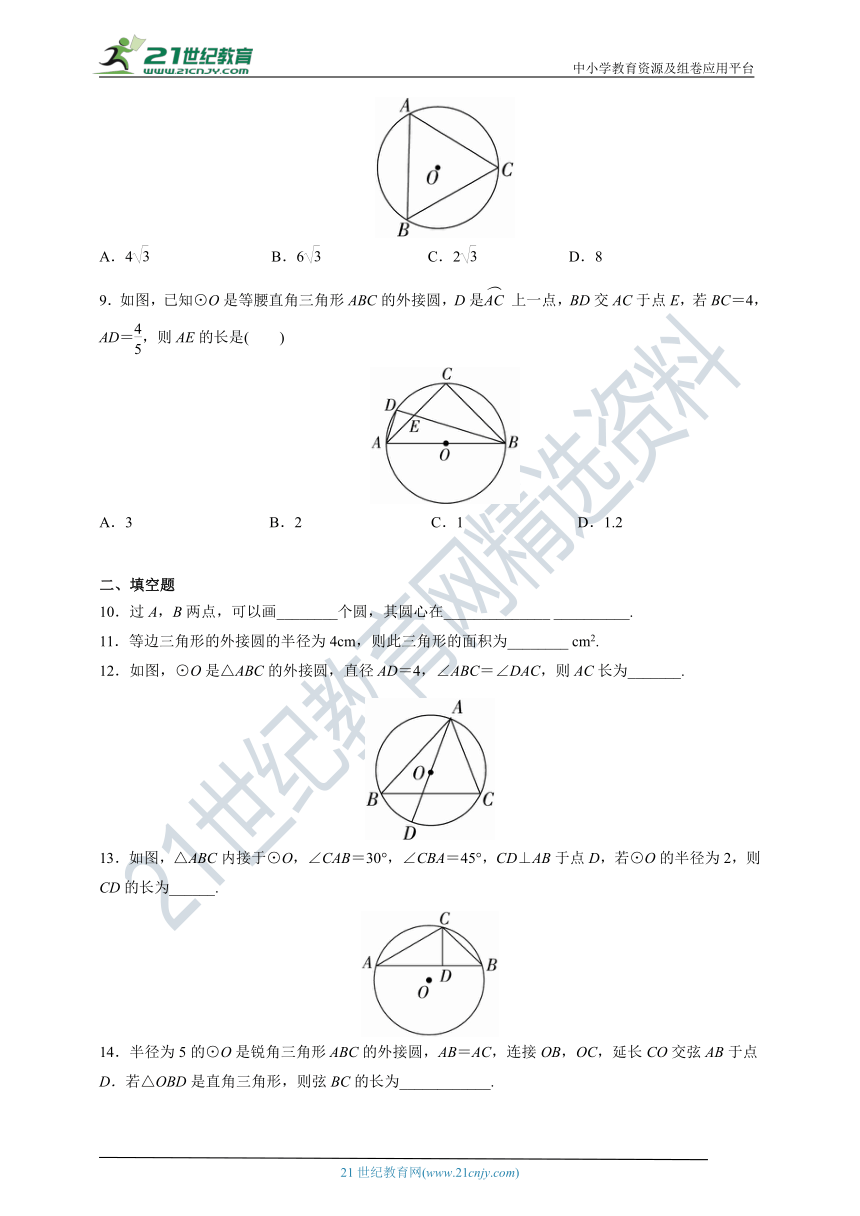
8.如图,⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4,则AC的长等于( )
A.4 B.6 C.2 D.8
9.如图,已知⊙O是等腰直角三角形ABC的外接圆,D是上一点,BD交AC于点E,若BC=4,AD=,则AE的长是( )
A.3 B.2 C.1 D.1.2
二、填空题
10.过A,B两点,可以画________个圆,其圆心在______________ __________.
11.等边三角形的外接圆的半径为4cm,则此三角形的面积为________ cm2.
12.如图,⊙O是△ABC的外接圆,直径AD=4,∠ABC=∠DAC,则AC长为_______.
13.如图,△ABC内接于⊙O,∠CAB=30°,∠CBA=45°,CD⊥AB于点D,若⊙O的半径为2,则CD的长为______.
14.半径为5的⊙O是锐角三角形ABC的外接圆,AB=AC,连接OB,OC,延长CO交弦AB于点D.若△OBD是直角三角形,则弦BC的长为____________.
三、解答题
15.如图,A,B,C是三个新建的居民住宅楼的所在地,现设想建立一个菜市场,使菜市场到三个居民住宅楼的距离相等,请问能否实现这一设想?若能,请设计并画出图形;若不能,请你说明理由.
16.如图,作一个圆,使它经过已知点A,B,且圆心在直线l上.
(1)当l与AB斜交时,可作出几个?
(2)当直线l和AB垂直但不经过AB的中点时,可作出几个?
(3)当直线l是AB的垂直平分线时又怎样呢?
17.如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以点D为圆心,以DB为半径的圆上?并说明理由.
18.如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙O于点D,交AC于点E,连接AD,BD,CD.
(1)求证:AD=CD;
(2)若AB=10,cos∠ABC=,求tan∠DBC的值.
参 考 答 案
1. D 2. C 3. C 4. B 5. B 6. C 7. C 8. A 9. C
10. 无数 AB的垂直平分线上
11. 12
12. 2
13.
14. 5或5
15. 解:能.只需作两边的垂直平分线,交点为O,然后以O为圆心,以OA长为半径作圆,那么点O就是所求的菜市场的位置.
16. 解:(1)当l与AB斜交时可作一个圆.
(2)不能作圆.
(3)可作无数个圆.
17. (1)证明:∵AD为直径,AD⊥BC,∴=.∴BD=CD.
(2)解:B,E,C三点在以点D为圆心,以DB为半径的圆上.理由:由(1),知=,∴∠BAD=∠CBD.又∵BE平分∠ABC,∴∠CBE=∠ABE.∵∠DBE=∠CBD+∠CBE,∠DEB=∠BAD+∠ABE,∴∠DBE=∠DEB.∴DB=DE.由(1),知BD=CD.∴DB=DE=DC.∴B,E,C三点在以点D为圆心,以DB为半径的圆上.
18.(1)证明:∵AB为⊙O的直径,∴∠ACB=90°.又∵OD∥BC,∴∠AEO=∠ACB=90°.∴OD⊥AC.∴=.∴AD=CD.
(2) 解:∵AB=10,∴OA=OD=AB=5.∵OD∥BC,∴∠AOE=∠ABC.在Rt△AEO中,OE=OA·cos∠AOE=OA·cos∠ABC=5×=3.∴DE=OD-OE=5-3=2.由勾股定理,得AE===4.在Rt△AED中,tan∠DAE===.又∵∠DBC=∠DAE,∴tan∠DBC=.
_21?????????è?????(www.21cnjy.com)_
2020-2021学年九年级数学下册课时作业(北师版)
第三章 圆
5 确定圆的条件
一、选择题
1.只能作一个圆的条件是( )
A.已知圆心 B.同一直线上的三点
C.已知半径 D.过不在同一直线上的三点
2.△ABC的外接圆的圆心在△ABC的外部,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.无法确定
3.下列说法正确的是( )
A.三角形的外心在三角形外
B.任意一个圆,有且只有一个内接三角形
C.任意一个三角形一定有一个外接圆,并且只有一个外接圆
D.三角形的外心是三边上的高的交点
4.小颖同学在手工制作中,把一个边长为12cm的等边三角形纸片贴到一个圆的纸片上,若三角形的三个顶点,恰好都在这个圆上,则圆的半径为( )
A.2cm B.4cm C.6cm D.8cm
5.小亮不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( )
A.第①块 B.第②块 C.第③块 D.第④块
6.在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,则它的外心与顶点C的距离为( )
A.3cm B.4cm C.5cm D.2.5cm
7.已知AB=5cm,则经过A,B两点,且半径为3cm的圆有( )
A.0个 B.1个 C.2个 D.无数个
8.如图,⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4,则AC的长等于( )
A.4 B.6 C.2 D.8
9.如图,已知⊙O是等腰直角三角形ABC的外接圆,D是上一点,BD交AC于点E,若BC=4,AD=,则AE的长是( )
A.3 B.2 C.1 D.1.2
二、填空题
10.过A,B两点,可以画________个圆,其圆心在______________ __________.
11.等边三角形的外接圆的半径为4cm,则此三角形的面积为________ cm2.
12.如图,⊙O是△ABC的外接圆,直径AD=4,∠ABC=∠DAC,则AC长为_______.
13.如图,△ABC内接于⊙O,∠CAB=30°,∠CBA=45°,CD⊥AB于点D,若⊙O的半径为2,则CD的长为______.
14.半径为5的⊙O是锐角三角形ABC的外接圆,AB=AC,连接OB,OC,延长CO交弦AB于点D.若△OBD是直角三角形,则弦BC的长为____________.
三、解答题
15.如图,A,B,C是三个新建的居民住宅楼的所在地,现设想建立一个菜市场,使菜市场到三个居民住宅楼的距离相等,请问能否实现这一设想?若能,请设计并画出图形;若不能,请你说明理由.
16.如图,作一个圆,使它经过已知点A,B,且圆心在直线l上.
(1)当l与AB斜交时,可作出几个?
(2)当直线l和AB垂直但不经过AB的中点时,可作出几个?
(3)当直线l是AB的垂直平分线时又怎样呢?
17.如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以点D为圆心,以DB为半径的圆上?并说明理由.
18.如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙O于点D,交AC于点E,连接AD,BD,CD.
(1)求证:AD=CD;
(2)若AB=10,cos∠ABC=,求tan∠DBC的值.
参 考 答 案
1. D 2. C 3. C 4. B 5. B 6. C 7. C 8. A 9. C
10. 无数 AB的垂直平分线上
11. 12
12. 2
13.
14. 5或5
15. 解:能.只需作两边的垂直平分线,交点为O,然后以O为圆心,以OA长为半径作圆,那么点O就是所求的菜市场的位置.
16. 解:(1)当l与AB斜交时可作一个圆.
(2)不能作圆.
(3)可作无数个圆.
17. (1)证明:∵AD为直径,AD⊥BC,∴=.∴BD=CD.
(2)解:B,E,C三点在以点D为圆心,以DB为半径的圆上.理由:由(1),知=,∴∠BAD=∠CBD.又∵BE平分∠ABC,∴∠CBE=∠ABE.∵∠DBE=∠CBD+∠CBE,∠DEB=∠BAD+∠ABE,∴∠DBE=∠DEB.∴DB=DE.由(1),知BD=CD.∴DB=DE=DC.∴B,E,C三点在以点D为圆心,以DB为半径的圆上.
18.(1)证明:∵AB为⊙O的直径,∴∠ACB=90°.又∵OD∥BC,∴∠AEO=∠ACB=90°.∴OD⊥AC.∴=.∴AD=CD.
(2) 解:∵AB=10,∴OA=OD=AB=5.∵OD∥BC,∴∠AOE=∠ABC.在Rt△AEO中,OE=OA·cos∠AOE=OA·cos∠ABC=5×=3.∴DE=OD-OE=5-3=2.由勾股定理,得AE===4.在Rt△AED中,tan∠DAE===.又∵∠DBC=∠DAE,∴tan∠DBC=.
_21?????????è?????(www.21cnjy.com)_
