2.6二次函数的应用(1)面积问题同步练习(含解析)
文档属性
| 名称 | 2.6二次函数的应用(1)面积问题同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 16:50:07 | ||
图片预览




文档简介
2.6二次函数的应用(1)面积问题
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,其中选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2019春?西湖区校级月考)有一个矩形苗圃园,其中一边靠墙,另外边用长为20m的篱笆围成.已知墙长为15m,若平行于墙的一边长不小于8m,则这个苗圃园面积的最大值和最小值分别为( )
A.48m2,37.5m2 B.50m2,32m2
C.50m2,37.5m2 D.48m2,32m2
2.(2019?宝安区二模)如图,小明想用长为12米的栅栏(虚线部分),借助围墙围成一个矩形花园ABCD,则矩形ABCD的最大面积是( )平方米.
A.16 B.18 C.20 D.24
3.(2019?桥西区校级模拟)如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,动点P从点A开始沿边AB向B以1cm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以2cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过( )秒,四边形APQC的面积最小.
A.1 B.2 C.3 D.4
4.(2018秋?大观区校级月考)用长度为8m的铝合金条制成如图所示的矩形窗框,那么这个窗户的最大透光面积为( )m2.
A.256 B.83 C.2 D.4
5.(2019?保定三模)某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为( )
A.75m2 B.752m2 C.48m2 D.2252m2
6.(2018秋?柯桥区期末)在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=m.若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积S的最大值为( )
A.193 B.194 C.195 D.196
7.(2007秋?吴中区期末)如图,在矩形ABCD中,AB=a,BC=b,b3≤a≤3b,AE=AH=CF=CG,则四边形EFGH的面积的最大值是( )
A.116(a+b)2 B.18(a+b)2 C.14(a+b)2 D.12(a+b)2
8.如图,△ABC是直角三角形,∠A=90°,AB=8cm,AC=6cm,点P从点A出发,沿AB方向以2cm/s的速度向点B运动;同时点Q从点A出发,沿AC方向以1cm/s的速度向点C运动,其中一个动点到达终点,则另一个动点也停止运动,则三角形APQ的最大面积是( )
A.8cm2 B.16cm2 C.24cm2 D.32cm2
9.(2019?江夏区模拟)如图,在△ABC中,AB=AC,BC=6,E为AC边上的点且AE=2EC,点D在BC边上且满足BD=DE,设BD=y,S△ABC=x,则y与x的函数关系式为( )
A.y=1810x2+52 B.y=4810x2+52
C.y=1810x2+2 D.y=4810x2+2
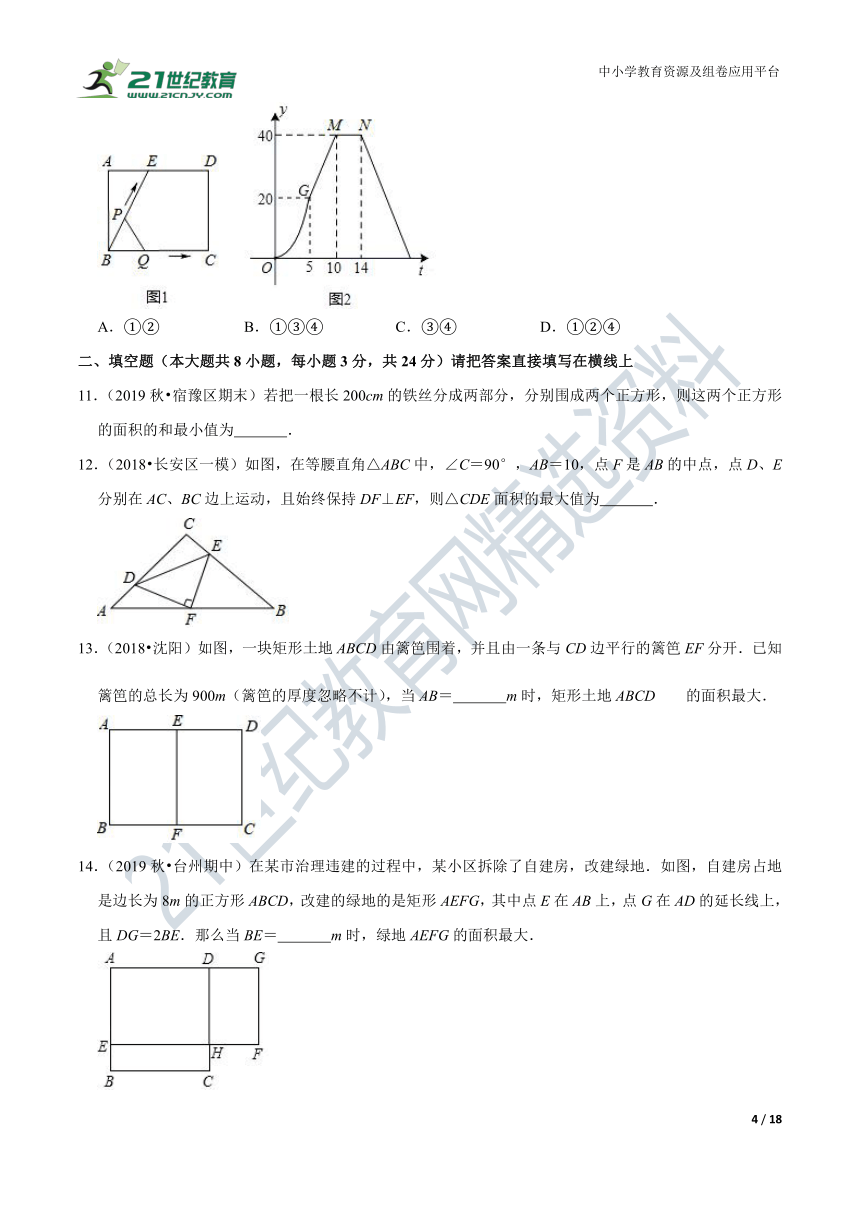
10.(2018?天心区校级一模)如图1所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE﹣ED﹣DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图2(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:①BE=BC; ②当t=6秒时,△ABE≌△PQB; ③点P运动了18秒; ④当t=272秒时,△ABE∽△QBP;其中正确的是( )
A.①② B.①③④ C.③④ D.①②④
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2019秋?宿豫区期末)若把一根长200cm的铁丝分成两部分,分别围成两个正方形,则这两个正方形的面积的和最小值为 .
12.(2018?长安区一模)如图,在等腰直角△ABC中,∠C=90°,AB=10,点F是AB的中点,点D、E分别在AC、BC边上运动,且始终保持DF⊥EF,则△CDE面积的最大值为 .
13.(2018?沈阳)如图,一块矩形土地ABCD由篱笆围着,并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900m(篱笆的厚度忽略不计),当AB= m时,矩形土地ABCD的面积最大.
14.(2019秋?台州期中)在某市治理违建的过程中,某小区拆除了自建房,改建绿地.如图,自建房占地是边长为8m的正方形ABCD,改建的绿地的是矩形AEFG,其中点E在AB上,点G在AD的延长线上,且DG=2BE.那么当BE= m时,绿地AEFG的面积最大.
15.(2019春?西湖区校级月考)用12m长的木材做窗框(如图所示),要使透过窗户的光线最多,窗框的长为 m,此时最大面积为 m2.
16.(2019?商南县二模)如图,菱形ABCD的边长为8,∠BAD=60°,点E是AD上一动点(不与A、D重合),点F是CD上一动点,且AE+CF=8,则△DEF面积的最大值为 .
17.(2019?兴庆区校级三模)已知如图,矩形ABCD的周长为18,其中E、F、G、H为矩形ABCD的各边中点,若AB=x,四边形EFGH的面积为y,则y与x之间的函数关系式为 .
18.(2019?温州模拟)为了节省材料,某农场主利用围墙(围墙足够长)为一边,用总长为80m的篱笆围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等,则能围成的矩形区域ABCD的面积最大值是 m2.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020?河池三模)如图,在足够大的空地上有一段长为100m的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100m的木栏
(1)若AD<20m,所围成的矩形菜园的面积为450m2,求所利用的旧墙AD的长.
(2)求矩形菜园ABCD面积的最大值.
20.(2020?宁波模拟)如图,是400米跑道示意图,中间的足球场ABCD是矩形,两边是半圆,直道AB的长是多少?
你一定知道是100米!可你也许不知道,这不仅仅为了比赛的需要,还有另外一个原因,等你做完本题就明白了.设AB=x米.
(1)请用含x的代数式表示BC.
(2)设矩形ABCD的面积为S.
①求出S关于x的函数表达式.
②当直道AB为多少米时,矩形ABCD的面积最大?
21.(2019秋?花都区期末)如图,将边长为40cm的正方形硬纸板的四个角各剪掉一个同样大小的正方形,剩余部分折成一个无盖的盒子.(纸板的厚度忽略不计).
(1)若该无盖盒子的底面积为900cm2,求剪掉的正方形的边长;
(2)求折成的无盖盒子的侧面积的最大值.
22.(2020春?道里区期末)某养鸡专业户用篱笆及一面墙(该墙可用最大长度为36米)围成一个矩形场地ABCD来供鸡室外活动,该场地中间隔有一道与AB平行的篱笆(EF),如图,BE、EF上各留有1米宽的门(门不需要篱笆),该养鸡专业户共用篱笆58米,设该矩形的一边AB长x米,AD>AB,矩形ABCD的面积为s平方米.
(1)求出S与x的函数关系式,直接写出自变量x的取值范围;
(2)若矩形ABCD的面积为252平方米,求AB的长.
23.(2020?无锡)有一块矩形地块ABCD,AB=20米,BC=30米.为美观,拟种植不同的花卉,如图所示,将矩形ABCD分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为x米.现决定在等腰梯形AEHD和BCGF中种植甲种花卉;在等腰梯形ABFE和CDHG中种植乙种花卉;在矩形EFGH中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元/米2、60元/米2、40元/米2,设三种花卉的种植总成本为y元.
(1)当x=5时,求种植总成本y;
(2)求种植总成本y与x的函数表达式,并写出自变量x的取值范围;
(3)若甲、乙两种花卉的种植面积之差不超过120平方米,求三种花卉的最低种植总成本.
24.(2019秋?南岸区期末)空地上有一段长为am的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,已知木栏总长为120m.
(1)已知a=30,矩形菜园的一边靠墙,另三边一共用了120m木栏,且围成的矩形菜园而积为1000m2.如图1,求所利用旧墙AD的长;
(2)已知0<a<60,且空地足够大,如图2.请你合理利用旧墙及所给木栏设计一个方案,使得所围成的矩形菜园ABCD的面积最大,并求面积的最大值.
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解析】设平行于墙的一边长为xm,苗圃园面积为Sm2,则
S=x×12(20﹣x)
=-12(x2﹣20x)
=-12(x﹣10)2+50 (8≤x≤15)
∵-12<0
∴S有最大值,x=10>8时,S最大=50
∵墙长为15m
∴当x=15时,S最小
S最小=15×12×(20﹣15)=37.5
∴这个苗圃园面积的最大值和最小值分别为50m2,37.5m2.
故选:C.
2.【解析】
设AB=x,则BC=12﹣2x
得矩形ABCD的面积:S=x(12﹣2x)=﹣2x2+12=﹣2(x﹣3)2+18
即矩形ABCD的最大面积为18平方米
故选:B.
3.【解析】设P、Q同时出发后经过的时间为ts,四边形APQC的面积为Scm2,则有:
S=S△ABC﹣S△PBQ
=12×12×6-12(6﹣t)×2t
=t2﹣6t+36
=(t﹣3)2+27.
∴当t=3s时,S取得最小值.
故选:C.
4.【解析】设宽为xm,则长为8-3x2m,
可得面积S=x?8-3x2=-32x2+4x,
当x=43时,S有最大值,最大值为-164×(-32)=83
故选:B.
5.【解析】设垂直于墙的材料长为x米,
则平行于墙的材料长为27+3﹣3x=30﹣3x,
则总面积S=x(30﹣3x)=﹣3x2+30x=﹣3(x﹣5)2+75,
故饲养室的最大面积为75平方米,
故选:A.
6.【解析】∵AB=m米,
∴BC=(28﹣m)米.
则S=AB?BC=m(28﹣m)=﹣m2+28m.
即S=﹣m2+28m(0<m<28).
由题意可知,m≥628-m≥15,
解得6≤m≤13.
∵在6≤m≤13内,S随m的增大而增大,
∴当m=13时,S最大值=195,
即花园面积的最大值为195m2.
故选:C.
7.【解析】设AE=AH=CF=CG=x,则BE=DG=a﹣x,BF=DH=b﹣x,
设四边形EFGH的面积为y,
依题意,得y=ab﹣x2﹣(a﹣x)(b﹣x),
即:y=﹣2x2+(a+b)x,
∵﹣2<0,抛物线开口向下,
∴x=a+b4时,有最大值,
∵b3≤a≤3b,
∴0<x≤a,
∴函数有最大值为-(a+b)24×(-2)=18(a+b)2.
故选:B.
8.【解析】根据题意
沿AB方向以2cm/s的速度向点B运动;同时点Q从点A出发,沿AC方向以1cm/s的速度向点C运动,
∴AP=2t,AQ=t,
S△APQ=t2,
∵0<t≤4,
∴三角形APQ的最大面积是16.
故选:B.
9.【解析】过A作AH⊥BC,过E作EP⊥BC,则AH∥EP,
∴HC=3,PC=1,BP=5,PE=13AH,
∵BD=DE=y,
∴在Rt△EDP中,y2=(5﹣y)2+PE2,
∵x=6AH÷2=3AH,
∴y2=(5﹣y)2+(19x)2,
∴y=1810x2+52,
故选:A.
10.【解析】观察图象可知,AD=BC=5×2=10,BE=1×10=10,ED=4×1=4,AE=10﹣4=6,
∴BE=BC,故①正确,
如图1中,当t=6秒时,点P在BE上,点Q静止于点C处,
在△ABE与△PQB中,
AE=PB=6∠1=∠2BE=BC,
∴△ABE≌△PQB(SAS),故②正确,
在Rt△ABE中,AB=BE2-AE2=102-62=8,
∴BE+DE+DC=10+4+8=22,
∴点P运动了22秒,故③错误,
当t=272秒时,点P在线段DE上,点Q与点C重合,此时∠PQB≠90°,
∴△ABE与△QBP不相似,故④错误.
∴①②正确,
故选:A.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解析】如图,设将铁丝分成xcm和(200﹣x)cm两部分,列方程得:
y=(x4)2+(200-x4)2=18(x﹣100)2+1250,
由于18>0,故其最小值为1250cm2,
故答案为:1250cm2.
12.【解析】如图所示,连接CF,
∵等腰直角△ABC中,∠C=90°,AB=10,点F是AB的中点,
∴CF=AF,∠A=∠FCE,AC=BC=10×22=52,
又∵∠DFC+∠CFE=90°,∠AFD+∠CFD=90°,
∴∠AFD=∠CFE,
∴△ADF≌△CEF(ASA),
设AD=x(0<x<52),△CDE的面积为y,则CE=x,CD=52-x,∠C=90°,
∴y=12x(52-x)=-12(x-522)2+254,
即△CDE面积的最大值为254,
故答案为:254.
13.【解析】设AB=xm,则BC=12(900﹣3x),
由题意可得,S=AB×BC=x×12(900﹣3x)=-32(x2﹣300x)=-32(x﹣150)2+33750
∴当x=150时,S取得最大值,此时,S=33750,
∴AB=150m,
故答案为:150.
14.【解析】设BE=xm,则DG=2BE=2xm,绿地AEFG的面积为ym2,根据题意得:
y=AE?AG
=(8﹣x)(8+2x)
=﹣2x2+8x+64
=﹣2(x﹣2)2+72.
∵二次项系数为﹣2,
∴当x=2时,y有最大值72.
故答案为:2.
15.【解析】设窗框的长为xm,则窗框的宽为13(12﹣2x),
所以,窗框的面积=13(12﹣2x)x=-23(x﹣3)2+6,
∵a=-23<0,
∴当x=3时,窗框的面积最大,透过窗户的光线最多,此时最大面积为6m2.
故答案为:3,6.
16.【解析】过点F作FG⊥AD交AD的延长线于点G,
∵菱形ABCD边长为8,∠BAD=60°,
∴AD=CD=8,∠ADC=180°﹣∠BAD=120°,
∴∠FDG=180°﹣∠ADB=60°,
设AE=x,
∵AE+CF=8,
∴CF=8﹣x;
∴DE=AD﹣AE=8﹣x,DF=CD﹣CF=8﹣(8﹣x)=x,
在Rt△DFG中,FG=DF?sin∠GDF=32x,
∴S△DEF=12DE?FG=12×(8﹣x)×32x=-34x2+23x=-34(x2﹣8x)=-34(x﹣4)2+43,
∴当x=4时,△DEF面积的最大,最大值为43.
故答案为:43.
17.【解析】∵矩形ABCD的周长为18,AB=x,
∴BC=12×18﹣x=9﹣x,
∵E、F、G、H为矩形ABCD的各边中点,
∴y=12x(9﹣x)=-12x2+92x,
故答案为:y=-12x2+92x;
18.【解析】如图,
∵三块矩形区域的面积相等,
∴矩形AEFD面积是矩形BCFE面积的2倍,
∴AE=2BE,
设BC=x,BE=FC=a,则AE=HG=DF=2a,
∴DF+FC+HG+AE+EB+EF+BC=80,即8a+2x=80,
∴a=-14x+10,3a=-34x+30,
∴矩形区域ABCD的面积S=(-34x+30)x=-34x2+30x,
∵a=-14x+10>0,
∴x<40,
则S=-34x2+30x(0<x<40);
∵S=-34x2+30x=-34(x﹣20)2+300(0<x<40),且二次项系数为-34<0,
∴当x=20时,S有最大值,最大值为300m2.
故答案为:300.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解析】(1)设AB=xm,则BC=(100﹣2x)m.
x(100﹣2x)=450.
解得,x1=5,x2=45,
当x=5时,100﹣2x=90>20,不合题意,舍去.
当x=45时,100﹣2x=10,
答:AD的长为10m;
(2)设AD=am,面积为Sm2,
S=a?100-a2=-12(a﹣50)2+1250,
∴当a=50时,S取得最大值,此时S=1250,
答:矩形菜园ABCD面积的最大值是1250m2.
20.【解析】(1)由题意可得:12π?BC=400-2x2,
∴BC=400-2xπ;
(2)①∵四边形ABCD是矩形,
∴S=400-2xπ×x=-2π(x﹣100)2+20000π;
②当x=100时,S最大,
∴当AB=100米时,S最大.
21.【解析】(1)设剪掉的正方形的边长为x cm,
则(40﹣2x)2=900,
即40﹣2x=±30,
解得x1=35(不合题意,舍去),x2=5;
答:剪掉的正方形边长为5cm;
(2)设剪掉的正方形的边长为x cm,盒子的侧面积为y cm2,
则y与x的函数关系式为y=4(40﹣2x)x,
即y=﹣8x2+160x,
y=﹣8(x﹣10)2+800,
∵﹣8<0,
∴y有最大值,
∴当x=10时,y最大=800;
答:折成的长方体盒子的侧面积有最大值,这个最大值是800cm2.
22.【解析】(1)由题意得:BC﹣1=58﹣x﹣x﹣(x﹣1),化简得,BC=60﹣3x,
可得矩形ABCD的面积:S=x(60﹣3x)=﹣3x2+60x(8≤x<15);
(2)由题意得:S=﹣3x2+60x=252,解得:x=14或6(舍去6),
故AB长为14米.
23.【解析】(1)当x=5时,EF=20﹣2x=10,EH=30﹣2x=20,
y=2×12(EH+AD)×20x+2×12(GH+CD)×x×60+EF?EH×40=(20+30)×5×20+(10+20)×5×60+20×10×40=22000;
(2)EF=(20﹣2x)米,EH=(30﹣2x)米,
参考(1),由题意得:y=(30+30﹣2x)?x?20+(20+20﹣2x)?x?60+(30﹣2x)(20﹣2x)?40=﹣400x+24000(0<x<10);
(3)S甲=2×12(EH+AD)×x=(30﹣2x+30)x=﹣2x2+60x,
同理S乙=﹣2x2+40x,
∵甲、乙两种花卉的种植面积之差不超过120米2,
∴﹣2x2+60x﹣(﹣2x2+40x)≤120,
解得:x≤6,
故0<x≤6,
而y=﹣400x+24000随x的增大而减小,故当x=6时,y的最小值为21600,
即三种花卉的最低种植总成本为21600元.
24.【解析】(1)设AD=x米,则AB=120-x2,
依题意得,x(120-x)2=1000,
解得x1=100,x2=20,
∵a=30,且x≤a,
∴x=100舍去,
∴利用旧墙AD的长为20米;
(2)设AD=x米,矩形ABCD的面积为S平方米,
①如果按图1案围成矩形菜园,依题意得,
S=x(120-x)2=-12(x-60)2+1800(0<x<a),
∵0<a<60,
∴x<a<60时,S随x的增大而增大,
当x=a时,S最大=60a-12a2,
②如按图2方案围成矩形菜园,依题意得,
S=x(120+a-2x)2=-(x-120+a4)2+(120+a)216(a≤x<120+a2),
当a<120+a4<120+a2时,即0<a<40时,
则x=120+a4时,S最大=(120+a)216=14400+240a+a216
当120+a4≤a,即40≤a<60时,S随x的增大而减小,
∴x=a时,S最大=-(a-120+a4)2+(120+a)216=60a-12a2,
综合①②,当0<a<40时,
14400+240a+a216-(60a-12a2)=9(a-40)216>0,
此时,按图2方案围成矩形菜园面积最大,最大面积为14400+240a+a216平方米,
当40≤a<60时,两种方案围成的矩形菜园面积最大值相等.
∴当0<a<40时,围成长和宽均为120+a4米的矩形菜园面积最大,最大面积为14400+240a+a216平方米;
当40≤a<60时,围成长为a米,宽为120-a2米的矩形菜园面积最大,最大面积为(60-12a2)平方米.
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,其中选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2019春?西湖区校级月考)有一个矩形苗圃园,其中一边靠墙,另外边用长为20m的篱笆围成.已知墙长为15m,若平行于墙的一边长不小于8m,则这个苗圃园面积的最大值和最小值分别为( )
A.48m2,37.5m2 B.50m2,32m2
C.50m2,37.5m2 D.48m2,32m2
2.(2019?宝安区二模)如图,小明想用长为12米的栅栏(虚线部分),借助围墙围成一个矩形花园ABCD,则矩形ABCD的最大面积是( )平方米.
A.16 B.18 C.20 D.24
3.(2019?桥西区校级模拟)如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,动点P从点A开始沿边AB向B以1cm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以2cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过( )秒,四边形APQC的面积最小.
A.1 B.2 C.3 D.4
4.(2018秋?大观区校级月考)用长度为8m的铝合金条制成如图所示的矩形窗框,那么这个窗户的最大透光面积为( )m2.
A.256 B.83 C.2 D.4
5.(2019?保定三模)某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为( )
A.75m2 B.752m2 C.48m2 D.2252m2
6.(2018秋?柯桥区期末)在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=m.若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积S的最大值为( )
A.193 B.194 C.195 D.196
7.(2007秋?吴中区期末)如图,在矩形ABCD中,AB=a,BC=b,b3≤a≤3b,AE=AH=CF=CG,则四边形EFGH的面积的最大值是( )
A.116(a+b)2 B.18(a+b)2 C.14(a+b)2 D.12(a+b)2
8.如图,△ABC是直角三角形,∠A=90°,AB=8cm,AC=6cm,点P从点A出发,沿AB方向以2cm/s的速度向点B运动;同时点Q从点A出发,沿AC方向以1cm/s的速度向点C运动,其中一个动点到达终点,则另一个动点也停止运动,则三角形APQ的最大面积是( )
A.8cm2 B.16cm2 C.24cm2 D.32cm2
9.(2019?江夏区模拟)如图,在△ABC中,AB=AC,BC=6,E为AC边上的点且AE=2EC,点D在BC边上且满足BD=DE,设BD=y,S△ABC=x,则y与x的函数关系式为( )
A.y=1810x2+52 B.y=4810x2+52
C.y=1810x2+2 D.y=4810x2+2
10.(2018?天心区校级一模)如图1所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE﹣ED﹣DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图2(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:①BE=BC; ②当t=6秒时,△ABE≌△PQB; ③点P运动了18秒; ④当t=272秒时,△ABE∽△QBP;其中正确的是( )
A.①② B.①③④ C.③④ D.①②④
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2019秋?宿豫区期末)若把一根长200cm的铁丝分成两部分,分别围成两个正方形,则这两个正方形的面积的和最小值为 .
12.(2018?长安区一模)如图,在等腰直角△ABC中,∠C=90°,AB=10,点F是AB的中点,点D、E分别在AC、BC边上运动,且始终保持DF⊥EF,则△CDE面积的最大值为 .
13.(2018?沈阳)如图,一块矩形土地ABCD由篱笆围着,并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900m(篱笆的厚度忽略不计),当AB= m时,矩形土地ABCD的面积最大.
14.(2019秋?台州期中)在某市治理违建的过程中,某小区拆除了自建房,改建绿地.如图,自建房占地是边长为8m的正方形ABCD,改建的绿地的是矩形AEFG,其中点E在AB上,点G在AD的延长线上,且DG=2BE.那么当BE= m时,绿地AEFG的面积最大.
15.(2019春?西湖区校级月考)用12m长的木材做窗框(如图所示),要使透过窗户的光线最多,窗框的长为 m,此时最大面积为 m2.
16.(2019?商南县二模)如图,菱形ABCD的边长为8,∠BAD=60°,点E是AD上一动点(不与A、D重合),点F是CD上一动点,且AE+CF=8,则△DEF面积的最大值为 .
17.(2019?兴庆区校级三模)已知如图,矩形ABCD的周长为18,其中E、F、G、H为矩形ABCD的各边中点,若AB=x,四边形EFGH的面积为y,则y与x之间的函数关系式为 .
18.(2019?温州模拟)为了节省材料,某农场主利用围墙(围墙足够长)为一边,用总长为80m的篱笆围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等,则能围成的矩形区域ABCD的面积最大值是 m2.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020?河池三模)如图,在足够大的空地上有一段长为100m的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100m的木栏
(1)若AD<20m,所围成的矩形菜园的面积为450m2,求所利用的旧墙AD的长.
(2)求矩形菜园ABCD面积的最大值.
20.(2020?宁波模拟)如图,是400米跑道示意图,中间的足球场ABCD是矩形,两边是半圆,直道AB的长是多少?
你一定知道是100米!可你也许不知道,这不仅仅为了比赛的需要,还有另外一个原因,等你做完本题就明白了.设AB=x米.
(1)请用含x的代数式表示BC.
(2)设矩形ABCD的面积为S.
①求出S关于x的函数表达式.
②当直道AB为多少米时,矩形ABCD的面积最大?
21.(2019秋?花都区期末)如图,将边长为40cm的正方形硬纸板的四个角各剪掉一个同样大小的正方形,剩余部分折成一个无盖的盒子.(纸板的厚度忽略不计).
(1)若该无盖盒子的底面积为900cm2,求剪掉的正方形的边长;
(2)求折成的无盖盒子的侧面积的最大值.
22.(2020春?道里区期末)某养鸡专业户用篱笆及一面墙(该墙可用最大长度为36米)围成一个矩形场地ABCD来供鸡室外活动,该场地中间隔有一道与AB平行的篱笆(EF),如图,BE、EF上各留有1米宽的门(门不需要篱笆),该养鸡专业户共用篱笆58米,设该矩形的一边AB长x米,AD>AB,矩形ABCD的面积为s平方米.
(1)求出S与x的函数关系式,直接写出自变量x的取值范围;
(2)若矩形ABCD的面积为252平方米,求AB的长.
23.(2020?无锡)有一块矩形地块ABCD,AB=20米,BC=30米.为美观,拟种植不同的花卉,如图所示,将矩形ABCD分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为x米.现决定在等腰梯形AEHD和BCGF中种植甲种花卉;在等腰梯形ABFE和CDHG中种植乙种花卉;在矩形EFGH中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元/米2、60元/米2、40元/米2,设三种花卉的种植总成本为y元.
(1)当x=5时,求种植总成本y;
(2)求种植总成本y与x的函数表达式,并写出自变量x的取值范围;
(3)若甲、乙两种花卉的种植面积之差不超过120平方米,求三种花卉的最低种植总成本.
24.(2019秋?南岸区期末)空地上有一段长为am的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,已知木栏总长为120m.
(1)已知a=30,矩形菜园的一边靠墙,另三边一共用了120m木栏,且围成的矩形菜园而积为1000m2.如图1,求所利用旧墙AD的长;
(2)已知0<a<60,且空地足够大,如图2.请你合理利用旧墙及所给木栏设计一个方案,使得所围成的矩形菜园ABCD的面积最大,并求面积的最大值.
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解析】设平行于墙的一边长为xm,苗圃园面积为Sm2,则
S=x×12(20﹣x)
=-12(x2﹣20x)
=-12(x﹣10)2+50 (8≤x≤15)
∵-12<0
∴S有最大值,x=10>8时,S最大=50
∵墙长为15m
∴当x=15时,S最小
S最小=15×12×(20﹣15)=37.5
∴这个苗圃园面积的最大值和最小值分别为50m2,37.5m2.
故选:C.
2.【解析】
设AB=x,则BC=12﹣2x
得矩形ABCD的面积:S=x(12﹣2x)=﹣2x2+12=﹣2(x﹣3)2+18
即矩形ABCD的最大面积为18平方米
故选:B.
3.【解析】设P、Q同时出发后经过的时间为ts,四边形APQC的面积为Scm2,则有:
S=S△ABC﹣S△PBQ
=12×12×6-12(6﹣t)×2t
=t2﹣6t+36
=(t﹣3)2+27.
∴当t=3s时,S取得最小值.
故选:C.
4.【解析】设宽为xm,则长为8-3x2m,
可得面积S=x?8-3x2=-32x2+4x,
当x=43时,S有最大值,最大值为-164×(-32)=83
故选:B.
5.【解析】设垂直于墙的材料长为x米,
则平行于墙的材料长为27+3﹣3x=30﹣3x,
则总面积S=x(30﹣3x)=﹣3x2+30x=﹣3(x﹣5)2+75,
故饲养室的最大面积为75平方米,
故选:A.
6.【解析】∵AB=m米,
∴BC=(28﹣m)米.
则S=AB?BC=m(28﹣m)=﹣m2+28m.
即S=﹣m2+28m(0<m<28).
由题意可知,m≥628-m≥15,
解得6≤m≤13.
∵在6≤m≤13内,S随m的增大而增大,
∴当m=13时,S最大值=195,
即花园面积的最大值为195m2.
故选:C.
7.【解析】设AE=AH=CF=CG=x,则BE=DG=a﹣x,BF=DH=b﹣x,
设四边形EFGH的面积为y,
依题意,得y=ab﹣x2﹣(a﹣x)(b﹣x),
即:y=﹣2x2+(a+b)x,
∵﹣2<0,抛物线开口向下,
∴x=a+b4时,有最大值,
∵b3≤a≤3b,
∴0<x≤a,
∴函数有最大值为-(a+b)24×(-2)=18(a+b)2.
故选:B.
8.【解析】根据题意
沿AB方向以2cm/s的速度向点B运动;同时点Q从点A出发,沿AC方向以1cm/s的速度向点C运动,
∴AP=2t,AQ=t,
S△APQ=t2,
∵0<t≤4,
∴三角形APQ的最大面积是16.
故选:B.
9.【解析】过A作AH⊥BC,过E作EP⊥BC,则AH∥EP,
∴HC=3,PC=1,BP=5,PE=13AH,
∵BD=DE=y,
∴在Rt△EDP中,y2=(5﹣y)2+PE2,
∵x=6AH÷2=3AH,
∴y2=(5﹣y)2+(19x)2,
∴y=1810x2+52,
故选:A.
10.【解析】观察图象可知,AD=BC=5×2=10,BE=1×10=10,ED=4×1=4,AE=10﹣4=6,
∴BE=BC,故①正确,
如图1中,当t=6秒时,点P在BE上,点Q静止于点C处,
在△ABE与△PQB中,
AE=PB=6∠1=∠2BE=BC,
∴△ABE≌△PQB(SAS),故②正确,
在Rt△ABE中,AB=BE2-AE2=102-62=8,
∴BE+DE+DC=10+4+8=22,
∴点P运动了22秒,故③错误,
当t=272秒时,点P在线段DE上,点Q与点C重合,此时∠PQB≠90°,
∴△ABE与△QBP不相似,故④错误.
∴①②正确,
故选:A.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解析】如图,设将铁丝分成xcm和(200﹣x)cm两部分,列方程得:
y=(x4)2+(200-x4)2=18(x﹣100)2+1250,
由于18>0,故其最小值为1250cm2,
故答案为:1250cm2.
12.【解析】如图所示,连接CF,
∵等腰直角△ABC中,∠C=90°,AB=10,点F是AB的中点,
∴CF=AF,∠A=∠FCE,AC=BC=10×22=52,
又∵∠DFC+∠CFE=90°,∠AFD+∠CFD=90°,
∴∠AFD=∠CFE,
∴△ADF≌△CEF(ASA),
设AD=x(0<x<52),△CDE的面积为y,则CE=x,CD=52-x,∠C=90°,
∴y=12x(52-x)=-12(x-522)2+254,
即△CDE面积的最大值为254,
故答案为:254.
13.【解析】设AB=xm,则BC=12(900﹣3x),
由题意可得,S=AB×BC=x×12(900﹣3x)=-32(x2﹣300x)=-32(x﹣150)2+33750
∴当x=150时,S取得最大值,此时,S=33750,
∴AB=150m,
故答案为:150.
14.【解析】设BE=xm,则DG=2BE=2xm,绿地AEFG的面积为ym2,根据题意得:
y=AE?AG
=(8﹣x)(8+2x)
=﹣2x2+8x+64
=﹣2(x﹣2)2+72.
∵二次项系数为﹣2,
∴当x=2时,y有最大值72.
故答案为:2.
15.【解析】设窗框的长为xm,则窗框的宽为13(12﹣2x),
所以,窗框的面积=13(12﹣2x)x=-23(x﹣3)2+6,
∵a=-23<0,
∴当x=3时,窗框的面积最大,透过窗户的光线最多,此时最大面积为6m2.
故答案为:3,6.
16.【解析】过点F作FG⊥AD交AD的延长线于点G,
∵菱形ABCD边长为8,∠BAD=60°,
∴AD=CD=8,∠ADC=180°﹣∠BAD=120°,
∴∠FDG=180°﹣∠ADB=60°,
设AE=x,
∵AE+CF=8,
∴CF=8﹣x;
∴DE=AD﹣AE=8﹣x,DF=CD﹣CF=8﹣(8﹣x)=x,
在Rt△DFG中,FG=DF?sin∠GDF=32x,
∴S△DEF=12DE?FG=12×(8﹣x)×32x=-34x2+23x=-34(x2﹣8x)=-34(x﹣4)2+43,
∴当x=4时,△DEF面积的最大,最大值为43.
故答案为:43.
17.【解析】∵矩形ABCD的周长为18,AB=x,
∴BC=12×18﹣x=9﹣x,
∵E、F、G、H为矩形ABCD的各边中点,
∴y=12x(9﹣x)=-12x2+92x,
故答案为:y=-12x2+92x;
18.【解析】如图,
∵三块矩形区域的面积相等,
∴矩形AEFD面积是矩形BCFE面积的2倍,
∴AE=2BE,
设BC=x,BE=FC=a,则AE=HG=DF=2a,
∴DF+FC+HG+AE+EB+EF+BC=80,即8a+2x=80,
∴a=-14x+10,3a=-34x+30,
∴矩形区域ABCD的面积S=(-34x+30)x=-34x2+30x,
∵a=-14x+10>0,
∴x<40,
则S=-34x2+30x(0<x<40);
∵S=-34x2+30x=-34(x﹣20)2+300(0<x<40),且二次项系数为-34<0,
∴当x=20时,S有最大值,最大值为300m2.
故答案为:300.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解析】(1)设AB=xm,则BC=(100﹣2x)m.
x(100﹣2x)=450.
解得,x1=5,x2=45,
当x=5时,100﹣2x=90>20,不合题意,舍去.
当x=45时,100﹣2x=10,
答:AD的长为10m;
(2)设AD=am,面积为Sm2,
S=a?100-a2=-12(a﹣50)2+1250,
∴当a=50时,S取得最大值,此时S=1250,
答:矩形菜园ABCD面积的最大值是1250m2.
20.【解析】(1)由题意可得:12π?BC=400-2x2,
∴BC=400-2xπ;
(2)①∵四边形ABCD是矩形,
∴S=400-2xπ×x=-2π(x﹣100)2+20000π;
②当x=100时,S最大,
∴当AB=100米时,S最大.
21.【解析】(1)设剪掉的正方形的边长为x cm,
则(40﹣2x)2=900,
即40﹣2x=±30,
解得x1=35(不合题意,舍去),x2=5;
答:剪掉的正方形边长为5cm;
(2)设剪掉的正方形的边长为x cm,盒子的侧面积为y cm2,
则y与x的函数关系式为y=4(40﹣2x)x,
即y=﹣8x2+160x,
y=﹣8(x﹣10)2+800,
∵﹣8<0,
∴y有最大值,
∴当x=10时,y最大=800;
答:折成的长方体盒子的侧面积有最大值,这个最大值是800cm2.
22.【解析】(1)由题意得:BC﹣1=58﹣x﹣x﹣(x﹣1),化简得,BC=60﹣3x,
可得矩形ABCD的面积:S=x(60﹣3x)=﹣3x2+60x(8≤x<15);
(2)由题意得:S=﹣3x2+60x=252,解得:x=14或6(舍去6),
故AB长为14米.
23.【解析】(1)当x=5时,EF=20﹣2x=10,EH=30﹣2x=20,
y=2×12(EH+AD)×20x+2×12(GH+CD)×x×60+EF?EH×40=(20+30)×5×20+(10+20)×5×60+20×10×40=22000;
(2)EF=(20﹣2x)米,EH=(30﹣2x)米,
参考(1),由题意得:y=(30+30﹣2x)?x?20+(20+20﹣2x)?x?60+(30﹣2x)(20﹣2x)?40=﹣400x+24000(0<x<10);
(3)S甲=2×12(EH+AD)×x=(30﹣2x+30)x=﹣2x2+60x,
同理S乙=﹣2x2+40x,
∵甲、乙两种花卉的种植面积之差不超过120米2,
∴﹣2x2+60x﹣(﹣2x2+40x)≤120,
解得:x≤6,
故0<x≤6,
而y=﹣400x+24000随x的增大而减小,故当x=6时,y的最小值为21600,
即三种花卉的最低种植总成本为21600元.
24.【解析】(1)设AD=x米,则AB=120-x2,
依题意得,x(120-x)2=1000,
解得x1=100,x2=20,
∵a=30,且x≤a,
∴x=100舍去,
∴利用旧墙AD的长为20米;
(2)设AD=x米,矩形ABCD的面积为S平方米,
①如果按图1案围成矩形菜园,依题意得,
S=x(120-x)2=-12(x-60)2+1800(0<x<a),
∵0<a<60,
∴x<a<60时,S随x的增大而增大,
当x=a时,S最大=60a-12a2,
②如按图2方案围成矩形菜园,依题意得,
S=x(120+a-2x)2=-(x-120+a4)2+(120+a)216(a≤x<120+a2),
当a<120+a4<120+a2时,即0<a<40时,
则x=120+a4时,S最大=(120+a)216=14400+240a+a216
当120+a4≤a,即40≤a<60时,S随x的增大而减小,
∴x=a时,S最大=-(a-120+a4)2+(120+a)216=60a-12a2,
综合①②,当0<a<40时,
14400+240a+a216-(60a-12a2)=9(a-40)216>0,
此时,按图2方案围成矩形菜园面积最大,最大面积为14400+240a+a216平方米,
当40≤a<60时,两种方案围成的矩形菜园面积最大值相等.
∴当0<a<40时,围成长和宽均为120+a4米的矩形菜园面积最大,最大面积为14400+240a+a216平方米;
当40≤a<60时,围成长为a米,宽为120-a2米的矩形菜园面积最大,最大面积为(60-12a2)平方米.
