2.7二次函数的应用(2)抛物型问题同步练习(含解析)
文档属性
| 名称 | 2.7二次函数的应用(2)抛物型问题同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 17:00:22 | ||
图片预览



文档简介
2.7二次函数的应用(2)抛物型问题
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,其中选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020?濮阳模拟)小明以二次函数y=2x2﹣4x+8的图象为灵感为“2017北京?房山国际葡萄酒大赛”设计了一款杯子,如图为杯子的设计稿,若AB=4,DE=3,则杯子的高CE为( )
A.14 B.11 C.6 D.3
2.(2019秋?武昌区校级期中)如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m.若水面再下降1.5m,水面宽度为( )m.
A.4.5 B.25 C.26 D.27
3.(2019秋?汾阳市期末)如图,某幢建筑物从2.25米高的窗口A用水管向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点M离墙1米,离地面3米,则水流下落点B离墙的距离OB是( )
A.2.5米 B.3米 C.3.5米 D.4米
4.(2020?山西)竖直上抛物体离地面的高度h(m)与运动时间t(s)之间的关系可以近似地用公式h=﹣5t2+v0t+h0表示,其中h0(m)是物体抛出时离地面的高度,v0(m/s)是物体抛出时的速度.某人将一个小球从距地面1.5m的高处以20m/s的速度竖直向上抛出,小球达到的离地面的最大高度为( )
A.23.5m B.22.5m C.21.5m D.20.5m
5.(2020?绵阳)三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为10米,孔顶离水面1.5米;当水位下降,大孔水面宽度为14米时,单个小孔的水面宽度为4米,若大孔水面宽度为20米,则单个小孔的水面宽度为( )
A.43米 B.52米 C.213米 D.7米
6.(2019秋?北京期末)小悦乘座中国最高的摩天轮“南昌之星”,从最低点开始旋转一圈,她离地面的高度y(米)与旋转时间x(分)之间的关系可以近似地用二次函数来刻画.经测试得出部分数据如表.根据函数模型和数据,可推断出南昌之星旋转一圈的时间大约是( )
x(分)
…
13.5
14.7
16.0
…
y(米)
…
156.25
159.85
158.33
…
A.32分 B.30分 C.15分 D.13分
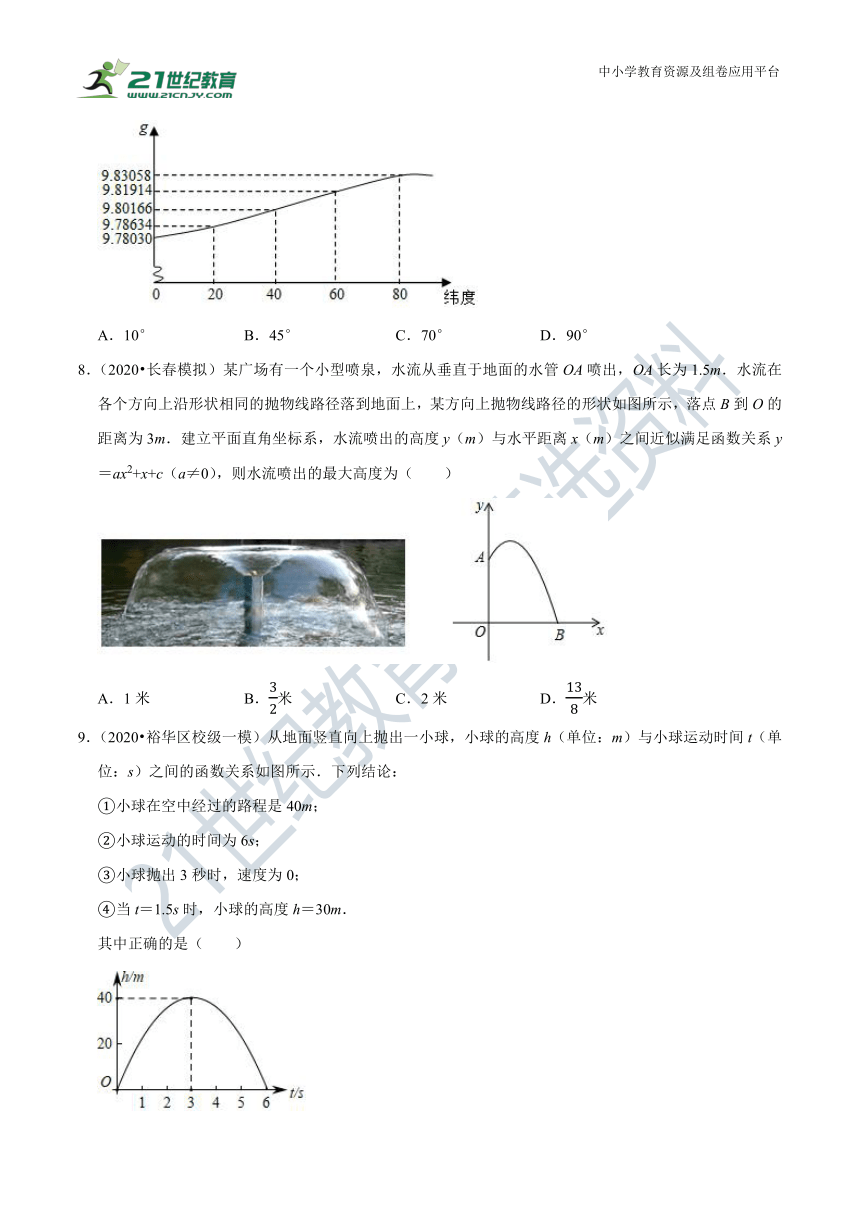
7.(2020?永康市模拟)已知物体下落时间t与下落距离x成以下关系:x=12gt2,其中g与纬度的关系如图.若一只熊掉进一个洞深为19.664m的洞,下落时间刚好为2s,这只熊最有可能生活在哪个纬度附近( )
A.10° B.45° C.70° D.90°
8.(2020?长春模拟)某广场有一个小型喷泉,水流从垂直于地面的水管OA喷出,OA长为1.5m.水流在各个方向上沿形状相同的抛物线路径落到地面上,某方向上抛物线路径的形状如图所示,落点B到O的距离为3m.建立平面直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间近似满足函数关系y=ax2+x+c(a≠0),则水流喷出的最大高度为( )
A.1米 B.32米 C.2米 D.138米
9.(2020?裕华区校级一模)从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是40m;
②小球运动的时间为6s;
③小球抛出3秒时,速度为0;
④当t=1.5s时,小球的高度h=30m.
其中正确的是( )
A.①④ B.①② C.②③④ D.②④
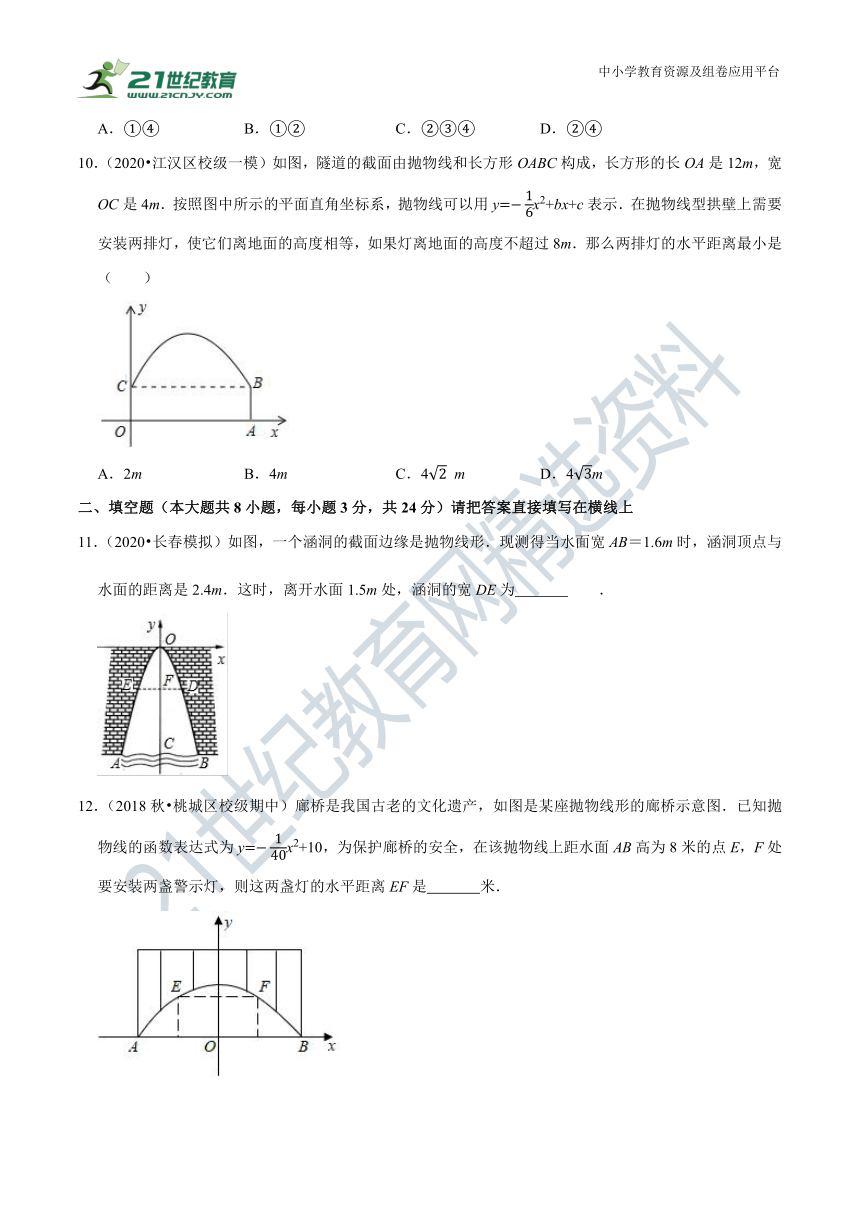
10.(2020?江汉区校级一模)如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m,宽OC是4m.按照图中所示的平面直角坐标系,抛物线可以用y=-16x2+bx+c表示.在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )
A.2m B.4m C.42 m D.43m
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020?长春模拟)如图,一个涵洞的截面边缘是抛物线形.现测得当水面宽AB=1.6m时,涵洞顶点与水面的距离是2.4m.这时,离开水面1.5m处,涵洞的宽DE为 .
12.(2018秋?桃城区校级期中)廊桥是我国古老的文化遗产,如图是某座抛物线形的廊桥示意图.已知抛物线的函数表达式为y=-140x2+10,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离EF是 米.
13.(2019秋?巴南区校级月考)汽车在高速公路刹车后滑行的距离y(米)与行驶的时间x(秒)的函数关系式是y=﹣3x2+36x,汽车刹车后,会继续向前滑行直至静止,那么汽车静止前2秒内滑行的距离是 米.
14.(2020?长春模拟)跳台滑雪是冬季奥运会比赛项目之一,运动员起跳后的飞行路线可以看作是抛物线的一部分,运动员起跳后的竖直高度y(单位:米)与水平距离x(单位:米)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某运动员起跳后的x与y的三组数据,根据上述函数模型和数据,可推断出该运动员起跳后飞行到最高点时,水平距离为 米.
15.(2019秋?建湖县期末)如图,有一个横截面边缘为抛物线的隧道入口,隧道入口处的底面宽度为8m,两侧距底面4m高处各有一盏灯,两灯间的水平距离为6m,则这个隧道入口的最大高度为 m(精确到0.1m).
16.(2020?李沧区模拟)如图,要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端A点安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为3m处达到最高,高度为5m,水柱落地处离池中心距离为9m,则水管的长度OA是 m.
17.(2020?长春模拟)如图,在喷水池的中心A处竖直安装一个水管AB,水管的顶端B处有一个喷水孔,喷出的抛物线形水柱在与池中心A的水平距离为1m处达到最高点C,高度为3m,水柱落地点D离池中心A处3m,则水管AB的长为 m.
18.(2018秋?富裕县期末)如图,是某公园一圆形喷水池,在池中心竖直安装一根水管OA=1.25m,A处是喷头,水流在各个方向沿形状相同的抛物线落下,水落地后形成一个圆,圆心为O,直径为线段CB.建立如图所示的平面直角坐标系,若水流路线达到最高处时,到x轴的距离为2.25m,到y轴的距离为1m,则水落地后形成的圆的直径CB= m.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020?顺德区三模)如图,隧道的截面由抛物线和长方形构成.长方形的长为16m,宽为6m,抛物线的最高点C离路面AA1的距离为8m.
(1)建立适当的坐标系,求出表示抛物线的函数表达式;
(2)一大型货车装载设备后高为7m,宽为4m.如果隧道内设双向行驶车道,那么这辆货车能否安全通过?
20.(2019秋?西城区校级期中)跳台滑雪是冬季奥运会比赛项目之一,运动员起跳后的飞行路线可以看作是抛物线的一部分.一名运动员起跳后,他的飞行路线如图所示,当他的水平距离为15m时,达到飞行的最高点C处,此时的竖直高度为45m,他落地时的水平距离(即OA的长)为60m,求这名运动员起跳时的竖直高度(即OB的长).
21.(2019秋?德城区校级期中)如图,隧道的截面由抛物线和矩形构成,AB=8m,BC=2m,隧道的最高点P位于AB的中点的正上方,且与AB的距离为4m.
(1)建立如图所示的坐标系,求图中抛物线的解析式;
(2)若隧道为单向通行,一辆高4米、宽3米的火车能否从隧道内通过?请说明理由.
22.(2020?市南区一模)如图,某小区在墙体OM上的点A处安装一抛物线型遮阳棚,现以地面和墙体分别为x轴和y轴建立直角坐标系,已知遮阳棚的高度y(m)与地面水平距离x(m)之间的关系式可以用y=-15x2+bx+c表示,且抛物线经过B(2,245),C(5,215).
请根据以上信息,解答下列问题:
(1)求抛物线的函数关系式;
(2)求遮阳棚跨度ON的长;
(3)现准备在抛物线上一点E处,安装一直角形钢架GEF对遮阳棚进行加固(点F,G分别在x轴,y轴上,且EG∥x轴,EF∥y轴),现有库存10米的钢材是否够用?
23.(2019秋?溧阳市期末)如图,某足球运动员站在点O处练习射门.将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)a= ,c= ;
(2)当足球飞行的时间为多少时,足球离地面最高?最大高度是多少?
(3)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?
24.(2020?绍兴)如图1,排球场长为18m,宽为9m,网高为2.24m,队员站在底线O点处发球,球从点O的正上方1.9m的C点发出,运动路线是抛物线的一部分,当球运动到最高点A时,高度为2.88m,即BA=2.88m,这时水平距离OB=7m,以直线OB为x轴,直线OC为y轴,建立平面直角坐标系,如图2.
(1)若球向正前方运动(即x轴垂直于底线),求球运动的高度y(m)与水平距离x(m)之间的函数关系式(不必写出x取值范围).并判断这次发球能否过网?是否出界?说明理由.
(2)若球过网后的落点是对方场地①号位内的点P(如图1,点P距底线1m,边线0.5m),问发球点O在底线上的哪个位置?(参考数据:2取1.4)
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解析】∵y=2x2﹣4x+8=2(x﹣1)2+6,
∴抛物线顶点D的坐标为(1,6),
∵AB=4,
∴B点的横坐标为x=3,
把x=3代入y=2x2﹣4x+8,得到y=14,
∴CD=14﹣6=8,
∴CE=CD+DE=8+3=11.
故选:B.
2.【解析】如图,以AB所在直线为x轴,以过拱顶C且垂直于AB的直线为y轴,建立平面直角坐标系,
则由题意可知A(﹣2,0),B(2,0),C(0,2),
设该抛物线的解析式为y=ax2+2,将B(2,0)代入得:
0=a×4+2,
解得:a=-12.
∴抛物线的解析式为y=-12x2+2,
∴若水面再下降1.5m,则有﹣1.5=-12x2+2,
解得:x=±7.
∵7-(-7)=27,
∴水面宽度为27m.
故选:D.
3.【解析】由题意可得,抛物线的顶点坐标为(1,3),
设抛物线的解析式为:y=a(x﹣1)2+3,
2.25=a(0﹣1)2+3,
解得a=﹣0.75,
∴y=-34(x﹣1)2+3,
当y=0时,-34(x﹣1)2+3=0,
解得,x1=﹣1,x2=3,
∴点B的坐标为(3,0),
∴OB=3,
答:水流下落点B离墙距离OB的长度是3米.
故选:B.
4.【解析】由题意可得,
h=﹣5t2+20t+1.5=﹣5(t﹣2)2+21.5,
因为a=﹣5<0,
故当t=2时,h取得最大值,此时h=21.5,
故选:C.
5.【解析】如图,建立如图所示的平面直角坐标系,由题意可得MN=4,EF=14,BC=10,DO=32,
设大孔所在抛物线解析式为y=ax2+32,
∵BC=10,
∴点B(﹣5,0),
∴0=a×(﹣5)2+32,
∴a=-350,
∴大孔所在抛物线解析式为y=-350x2+32,
设点A(b,0),则设顶点为A的小孔所在抛物线的解析式为y=m(x﹣b)2,
∵EF=14,
∴点E的横坐标为﹣7,
∴点E坐标为(﹣7,-3625),
∴-3625=m(x﹣b)2,
∴x1=65-1m+b,x2=-65-1m+b,
∴MN=4,
∴|65-1m+b﹣(-65-1m+b)|=4
∴m=-925,
∴顶点为A的小孔所在抛物线的解析式为y=-925(x﹣b)2,
∵大孔水面宽度为20米,
∴当x=﹣10时,y=-92,
∴-92=-925(x﹣b)2,
∴x1=522+b,x2=-522+b,
∴单个小孔的水面宽度=|(522+b)﹣(-522+b)|=52(米),
故选:B.
6.【解析】最值在自变量大于13.5小于14.7之间,
所以最接近摩天轮转一圈的时间的是15×2=30分钟.
故选:B.
7.【解析】∵若一只熊掉进一个洞深为19.664m的洞,下落时间刚好为2s,
∴x=19.664,t=2s,代入x=12gt2,得:
19.664=12g×22
∴g=9.832,
由图可知g=9.83058时,纬度为80,9.832比9.83058略大,
∴这只熊最有可能生活在纬度为90附近.
故选:D.
8.【解析】由题意可得,抛物线经过点(0,1.5)和(3,0),
把上述两个点坐标代入二次函数表达式得:
c=1.59a+3+c=0,
解得:a=-12c=32,
∴函数表达式为:y=-12x2+x+32,
=-12(x﹣1)2+2,
∵a<0,故函数有最大值,
∴当x=1时,y取得最大值,此时y=2,
答:水流喷出的最大高度为2米.
故选:C.
9.【解析】①由图象可知,小球在空中达到的最大高度为40m,则小球在空中经过的路程一定大于40m,故①错误;
②由图象可知,小球6s时落地,故小球运动的时间为6s,故②正确;
③小球抛出3秒时达到最高点,即速度为0,故③正确;
④设函数解析式为h=a(t﹣3)2+40,将(0,0)代入得:
0=a(0﹣3)2+40,
解得a=-409,
∴函数解析式为h=-409(t﹣3)2+40,
∴当t=1.5s时,h=-409(1.5﹣3)2+40=30,
∴④正确.
综上,正确的有②③④.
故选:C.
10.【解析】根据题意,得
OA=12,OC=4.
所以抛物线的顶点横坐标为6,
即-b2a=b13=6,
∴b=2,
∵C(0,4),
∴c=4,
所以抛物线解析式为:
y=-16x2+2x+4
=-16(x﹣6)2+10
当y=8时,
8=-16(x﹣6)2+10,
解得x1=6+23,x2=6﹣23.
则x1﹣x2=43.
所以两排灯的水平距离最小是43.
故选:D.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解析】∵抛物线y=ax2(a<0),
点B在抛物线上,将B(0.8,﹣2.4),
它的坐标代入y=ax2(a<0),
求得a=-154,
所求解析式为y=-154x2.
再由条件设D点坐标为(x,﹣0.9),
则有:﹣0.9=-154x2.,
解得:x=±65,
所以宽度为265,
故答案为:265.
12.【解析】令y=8,即y=-140x2+10=8,
解得:x=±45,
∴则EF=45-(﹣45)=85.
13.【解析】y=﹣3x2+36x=﹣3(x﹣6)2+108,
∴x=6(秒)时,汽车静止,此时滑行了108(米),
故当x=4(秒)时,y=﹣3x2+36x=96(米),
故汽车静止前2秒内滑行的距离是108﹣96=12(米),
故答案为12.
14.【解析】根据题意知,抛物线y=ax2+bx+c(a≠0)经过点(0,54.0)、(40,46.2)、(20,57.9),
则c=54.01600a+40b+c=46.2400a+20b+c=57.9,
解得:a=-0.0195b=0.585c=54.0,
所以x=-b2a=-0.5852×(-0.0195)=15(m).
故答案为:15.
15.【解析】建立如图所示的平面直角坐标系.
由题意可知各点的坐标,A(﹣4,0),B(4,0),D(﹣3,4).
设抛物线的解析式为:y=ax2+c(a≠0),把B(4,0),D(﹣3,4)代入,得
16a+c=09a+c=4,
解得a=-47c=647,
∴该抛物线的解析式为:y=-47x2+647,
则C(0,647).
∵647m≈9.1m.
故答案为:9.1.
16.【解析】设抛物线的表达式为:y=a(x﹣h)2+k=a(x﹣3)2+5,
将点(9,0)代入上式并解得:a=-536,
故抛物线的表达式为:y=-536(x﹣3)2+5,
令x=0,则y=154,即OA=154,
故答案为154.
17.【解析】以池中心为原点,竖直安装的水管为y轴,与水管垂直的为x轴建立直角坐标系.
由于在距池中心的水平距离为1m时达到最高,高度为3m,
则设抛物线的解析式为:y=a(x﹣1)2+3,
代入(3,0)求得:a=-34(x﹣1)2+3.
将a值代入得到抛物线的解析式为:y=-34(x﹣1)2+3(0≤x≤3);
令x=0,则y=-34+3=2.25.
故水管AB的长为2.25m.
故答案为:2.25.
18.【解析】设y轴右侧的抛物线解析式为:y=a(x﹣1)2+2.25
∵点A(0,1.25)在抛物线上
∴1.25=a(0﹣1)2+2.25
解得:a=﹣1
∴抛物线的解析式为:y=﹣(x﹣1)2+2.25
令y=0得:0=﹣(x﹣1)2+2.25
解得:x=2.5或x=﹣0.5(舍去)
∴点B坐标为(﹣2.5,0)
∴OB=OC=2.5
∴CB=5
故答案为:5.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解析】(1)如图,以AA1所在直线为x轴,以线段AA1的中点为坐标原点建立平面直角坐标系,
根据题意得A(﹣8,0),B(﹣8,6),C(0,8),
设抛物线的解析式为y=ax2+8,把B(﹣8,6)代入,得:
64a+8=6,
解得:a=-132.
∴抛物线的解析式为y=-132x2+8.
(2)根据题意,把x=±4代入解析式y=-132x2+8,
得y=7.5m.
∵7.5m>7m,
∴货运卡车能通过.
20.【解析】设抛物线的解析式为y=a(x﹣h)2+k,
根据题意得:抛物线的顶点坐标为(15,45),
∴y=a(x﹣15)2+45,
∵与x轴交于点A(60,0),
∴0=a(60﹣15)2+45,
解得:a=-145,
∴解析式为y=-145(x﹣15)2+45,
令x=0得:y=-145(0﹣15)2+45=40,
∴点B的坐标为(0,40),
∴这名运动员起跳时的竖直高度为40米.
21.【解析】(1)由题意可知,抛物线的顶点坐标(4,6),
设抛物线的方程为y=a(x﹣4)2+6,
又因为点A(0,2)在抛物线上,
所以有2=a(0﹣4)2+6.
所以a=-14.
因此有:y=-14(x-4)2+6;
(2)令y=4,则有4=-14(x-4)2+6,
解得:x1=4+22,x2=4-22,|x1-x2|=42>3,
∴货车可以通过.
22.【解析】(1)将点B、C的坐标代入抛物线表达式得:245=-45+2b+c215=-5+5b+c,解得b=65c=165,
故抛物线的表达式为:y=-15x2+65x+165;
(2)y=-15x2+65x+165,
令y=0,解得:x=﹣2(舍去)或8,
故ON=8;
(3)设点E(x,-15x2+65x+165),
由题意得:GE+EF=x-15x2+65x+165=-15(x-112)2+374
∵-15<0,
∴GE+EF的最大值为374,
∵374<10,
故现有库存10米的钢材够用.
23.【解析】(1)由题意得:函数y=at2+5t+c的图象经过(0,0.5)(0.8,3.5),
∴0.5=c3.5=0.82a+5×0.8+c,
解得:a=-2516c=12,
∴抛物线的解析式为:y=-2516t2+5t+12,
故答案为:-2516,12;
(2)∵y=-2516t2+5t+12,
∴y=-2516(t-85)2+92,
∴当t=85时,y最大=4.5,
∴当足球飞行的时间85s时,足球离地面最高,最大高度是4.5m;
(3)把x=28代入x=10t得t=2.8,
∴当t=2.8时,y=-2516×2.82+5×2.8+12=2.25<2.44,
∴他能将球直接射入球门.
24.【解析】(1)设抛物线的表达式为:y=a(x﹣7)2+2.88,
将x=0,y=1.9代入上式并解得:a=-150,
故抛物线的表达式为:y=-150(x﹣7)2+2.88;
当x=9时,y=-150(x﹣7)2+2.88=2.8>2.24,
当x=18时,y=-150(x﹣7)2+2.88=0.46>0,
故这次发球过网,但是出界了;
(2)如图,分别过点O,P作边线的平行线交于点Q,
在Rt△OPQ中,OQ=18﹣1=17,
当y=0时,-150(x﹣7)2+2.88=0,解得:x=19或﹣5(舍去﹣5),
∴OP=19,而OQ=17,
故PQ=62=8.4,
∵9﹣8.4﹣0.5=0.1,
∴发球点O在底线上且距右边线0.1米处.
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,其中选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020?濮阳模拟)小明以二次函数y=2x2﹣4x+8的图象为灵感为“2017北京?房山国际葡萄酒大赛”设计了一款杯子,如图为杯子的设计稿,若AB=4,DE=3,则杯子的高CE为( )
A.14 B.11 C.6 D.3
2.(2019秋?武昌区校级期中)如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m.若水面再下降1.5m,水面宽度为( )m.
A.4.5 B.25 C.26 D.27
3.(2019秋?汾阳市期末)如图,某幢建筑物从2.25米高的窗口A用水管向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点M离墙1米,离地面3米,则水流下落点B离墙的距离OB是( )
A.2.5米 B.3米 C.3.5米 D.4米
4.(2020?山西)竖直上抛物体离地面的高度h(m)与运动时间t(s)之间的关系可以近似地用公式h=﹣5t2+v0t+h0表示,其中h0(m)是物体抛出时离地面的高度,v0(m/s)是物体抛出时的速度.某人将一个小球从距地面1.5m的高处以20m/s的速度竖直向上抛出,小球达到的离地面的最大高度为( )
A.23.5m B.22.5m C.21.5m D.20.5m
5.(2020?绵阳)三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为10米,孔顶离水面1.5米;当水位下降,大孔水面宽度为14米时,单个小孔的水面宽度为4米,若大孔水面宽度为20米,则单个小孔的水面宽度为( )
A.43米 B.52米 C.213米 D.7米
6.(2019秋?北京期末)小悦乘座中国最高的摩天轮“南昌之星”,从最低点开始旋转一圈,她离地面的高度y(米)与旋转时间x(分)之间的关系可以近似地用二次函数来刻画.经测试得出部分数据如表.根据函数模型和数据,可推断出南昌之星旋转一圈的时间大约是( )
x(分)
…
13.5
14.7
16.0
…
y(米)
…
156.25
159.85
158.33
…
A.32分 B.30分 C.15分 D.13分
7.(2020?永康市模拟)已知物体下落时间t与下落距离x成以下关系:x=12gt2,其中g与纬度的关系如图.若一只熊掉进一个洞深为19.664m的洞,下落时间刚好为2s,这只熊最有可能生活在哪个纬度附近( )
A.10° B.45° C.70° D.90°
8.(2020?长春模拟)某广场有一个小型喷泉,水流从垂直于地面的水管OA喷出,OA长为1.5m.水流在各个方向上沿形状相同的抛物线路径落到地面上,某方向上抛物线路径的形状如图所示,落点B到O的距离为3m.建立平面直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间近似满足函数关系y=ax2+x+c(a≠0),则水流喷出的最大高度为( )
A.1米 B.32米 C.2米 D.138米
9.(2020?裕华区校级一模)从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是40m;
②小球运动的时间为6s;
③小球抛出3秒时,速度为0;
④当t=1.5s时,小球的高度h=30m.
其中正确的是( )
A.①④ B.①② C.②③④ D.②④
10.(2020?江汉区校级一模)如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m,宽OC是4m.按照图中所示的平面直角坐标系,抛物线可以用y=-16x2+bx+c表示.在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )
A.2m B.4m C.42 m D.43m
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020?长春模拟)如图,一个涵洞的截面边缘是抛物线形.现测得当水面宽AB=1.6m时,涵洞顶点与水面的距离是2.4m.这时,离开水面1.5m处,涵洞的宽DE为 .
12.(2018秋?桃城区校级期中)廊桥是我国古老的文化遗产,如图是某座抛物线形的廊桥示意图.已知抛物线的函数表达式为y=-140x2+10,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离EF是 米.
13.(2019秋?巴南区校级月考)汽车在高速公路刹车后滑行的距离y(米)与行驶的时间x(秒)的函数关系式是y=﹣3x2+36x,汽车刹车后,会继续向前滑行直至静止,那么汽车静止前2秒内滑行的距离是 米.
14.(2020?长春模拟)跳台滑雪是冬季奥运会比赛项目之一,运动员起跳后的飞行路线可以看作是抛物线的一部分,运动员起跳后的竖直高度y(单位:米)与水平距离x(单位:米)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某运动员起跳后的x与y的三组数据,根据上述函数模型和数据,可推断出该运动员起跳后飞行到最高点时,水平距离为 米.
15.(2019秋?建湖县期末)如图,有一个横截面边缘为抛物线的隧道入口,隧道入口处的底面宽度为8m,两侧距底面4m高处各有一盏灯,两灯间的水平距离为6m,则这个隧道入口的最大高度为 m(精确到0.1m).
16.(2020?李沧区模拟)如图,要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端A点安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为3m处达到最高,高度为5m,水柱落地处离池中心距离为9m,则水管的长度OA是 m.
17.(2020?长春模拟)如图,在喷水池的中心A处竖直安装一个水管AB,水管的顶端B处有一个喷水孔,喷出的抛物线形水柱在与池中心A的水平距离为1m处达到最高点C,高度为3m,水柱落地点D离池中心A处3m,则水管AB的长为 m.
18.(2018秋?富裕县期末)如图,是某公园一圆形喷水池,在池中心竖直安装一根水管OA=1.25m,A处是喷头,水流在各个方向沿形状相同的抛物线落下,水落地后形成一个圆,圆心为O,直径为线段CB.建立如图所示的平面直角坐标系,若水流路线达到最高处时,到x轴的距离为2.25m,到y轴的距离为1m,则水落地后形成的圆的直径CB= m.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020?顺德区三模)如图,隧道的截面由抛物线和长方形构成.长方形的长为16m,宽为6m,抛物线的最高点C离路面AA1的距离为8m.
(1)建立适当的坐标系,求出表示抛物线的函数表达式;
(2)一大型货车装载设备后高为7m,宽为4m.如果隧道内设双向行驶车道,那么这辆货车能否安全通过?
20.(2019秋?西城区校级期中)跳台滑雪是冬季奥运会比赛项目之一,运动员起跳后的飞行路线可以看作是抛物线的一部分.一名运动员起跳后,他的飞行路线如图所示,当他的水平距离为15m时,达到飞行的最高点C处,此时的竖直高度为45m,他落地时的水平距离(即OA的长)为60m,求这名运动员起跳时的竖直高度(即OB的长).
21.(2019秋?德城区校级期中)如图,隧道的截面由抛物线和矩形构成,AB=8m,BC=2m,隧道的最高点P位于AB的中点的正上方,且与AB的距离为4m.
(1)建立如图所示的坐标系,求图中抛物线的解析式;
(2)若隧道为单向通行,一辆高4米、宽3米的火车能否从隧道内通过?请说明理由.
22.(2020?市南区一模)如图,某小区在墙体OM上的点A处安装一抛物线型遮阳棚,现以地面和墙体分别为x轴和y轴建立直角坐标系,已知遮阳棚的高度y(m)与地面水平距离x(m)之间的关系式可以用y=-15x2+bx+c表示,且抛物线经过B(2,245),C(5,215).
请根据以上信息,解答下列问题:
(1)求抛物线的函数关系式;
(2)求遮阳棚跨度ON的长;
(3)现准备在抛物线上一点E处,安装一直角形钢架GEF对遮阳棚进行加固(点F,G分别在x轴,y轴上,且EG∥x轴,EF∥y轴),现有库存10米的钢材是否够用?
23.(2019秋?溧阳市期末)如图,某足球运动员站在点O处练习射门.将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)a= ,c= ;
(2)当足球飞行的时间为多少时,足球离地面最高?最大高度是多少?
(3)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?
24.(2020?绍兴)如图1,排球场长为18m,宽为9m,网高为2.24m,队员站在底线O点处发球,球从点O的正上方1.9m的C点发出,运动路线是抛物线的一部分,当球运动到最高点A时,高度为2.88m,即BA=2.88m,这时水平距离OB=7m,以直线OB为x轴,直线OC为y轴,建立平面直角坐标系,如图2.
(1)若球向正前方运动(即x轴垂直于底线),求球运动的高度y(m)与水平距离x(m)之间的函数关系式(不必写出x取值范围).并判断这次发球能否过网?是否出界?说明理由.
(2)若球过网后的落点是对方场地①号位内的点P(如图1,点P距底线1m,边线0.5m),问发球点O在底线上的哪个位置?(参考数据:2取1.4)
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解析】∵y=2x2﹣4x+8=2(x﹣1)2+6,
∴抛物线顶点D的坐标为(1,6),
∵AB=4,
∴B点的横坐标为x=3,
把x=3代入y=2x2﹣4x+8,得到y=14,
∴CD=14﹣6=8,
∴CE=CD+DE=8+3=11.
故选:B.
2.【解析】如图,以AB所在直线为x轴,以过拱顶C且垂直于AB的直线为y轴,建立平面直角坐标系,
则由题意可知A(﹣2,0),B(2,0),C(0,2),
设该抛物线的解析式为y=ax2+2,将B(2,0)代入得:
0=a×4+2,
解得:a=-12.
∴抛物线的解析式为y=-12x2+2,
∴若水面再下降1.5m,则有﹣1.5=-12x2+2,
解得:x=±7.
∵7-(-7)=27,
∴水面宽度为27m.
故选:D.
3.【解析】由题意可得,抛物线的顶点坐标为(1,3),
设抛物线的解析式为:y=a(x﹣1)2+3,
2.25=a(0﹣1)2+3,
解得a=﹣0.75,
∴y=-34(x﹣1)2+3,
当y=0时,-34(x﹣1)2+3=0,
解得,x1=﹣1,x2=3,
∴点B的坐标为(3,0),
∴OB=3,
答:水流下落点B离墙距离OB的长度是3米.
故选:B.
4.【解析】由题意可得,
h=﹣5t2+20t+1.5=﹣5(t﹣2)2+21.5,
因为a=﹣5<0,
故当t=2时,h取得最大值,此时h=21.5,
故选:C.
5.【解析】如图,建立如图所示的平面直角坐标系,由题意可得MN=4,EF=14,BC=10,DO=32,
设大孔所在抛物线解析式为y=ax2+32,
∵BC=10,
∴点B(﹣5,0),
∴0=a×(﹣5)2+32,
∴a=-350,
∴大孔所在抛物线解析式为y=-350x2+32,
设点A(b,0),则设顶点为A的小孔所在抛物线的解析式为y=m(x﹣b)2,
∵EF=14,
∴点E的横坐标为﹣7,
∴点E坐标为(﹣7,-3625),
∴-3625=m(x﹣b)2,
∴x1=65-1m+b,x2=-65-1m+b,
∴MN=4,
∴|65-1m+b﹣(-65-1m+b)|=4
∴m=-925,
∴顶点为A的小孔所在抛物线的解析式为y=-925(x﹣b)2,
∵大孔水面宽度为20米,
∴当x=﹣10时,y=-92,
∴-92=-925(x﹣b)2,
∴x1=522+b,x2=-522+b,
∴单个小孔的水面宽度=|(522+b)﹣(-522+b)|=52(米),
故选:B.
6.【解析】最值在自变量大于13.5小于14.7之间,
所以最接近摩天轮转一圈的时间的是15×2=30分钟.
故选:B.
7.【解析】∵若一只熊掉进一个洞深为19.664m的洞,下落时间刚好为2s,
∴x=19.664,t=2s,代入x=12gt2,得:
19.664=12g×22
∴g=9.832,
由图可知g=9.83058时,纬度为80,9.832比9.83058略大,
∴这只熊最有可能生活在纬度为90附近.
故选:D.
8.【解析】由题意可得,抛物线经过点(0,1.5)和(3,0),
把上述两个点坐标代入二次函数表达式得:
c=1.59a+3+c=0,
解得:a=-12c=32,
∴函数表达式为:y=-12x2+x+32,
=-12(x﹣1)2+2,
∵a<0,故函数有最大值,
∴当x=1时,y取得最大值,此时y=2,
答:水流喷出的最大高度为2米.
故选:C.
9.【解析】①由图象可知,小球在空中达到的最大高度为40m,则小球在空中经过的路程一定大于40m,故①错误;
②由图象可知,小球6s时落地,故小球运动的时间为6s,故②正确;
③小球抛出3秒时达到最高点,即速度为0,故③正确;
④设函数解析式为h=a(t﹣3)2+40,将(0,0)代入得:
0=a(0﹣3)2+40,
解得a=-409,
∴函数解析式为h=-409(t﹣3)2+40,
∴当t=1.5s时,h=-409(1.5﹣3)2+40=30,
∴④正确.
综上,正确的有②③④.
故选:C.
10.【解析】根据题意,得
OA=12,OC=4.
所以抛物线的顶点横坐标为6,
即-b2a=b13=6,
∴b=2,
∵C(0,4),
∴c=4,
所以抛物线解析式为:
y=-16x2+2x+4
=-16(x﹣6)2+10
当y=8时,
8=-16(x﹣6)2+10,
解得x1=6+23,x2=6﹣23.
则x1﹣x2=43.
所以两排灯的水平距离最小是43.
故选:D.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解析】∵抛物线y=ax2(a<0),
点B在抛物线上,将B(0.8,﹣2.4),
它的坐标代入y=ax2(a<0),
求得a=-154,
所求解析式为y=-154x2.
再由条件设D点坐标为(x,﹣0.9),
则有:﹣0.9=-154x2.,
解得:x=±65,
所以宽度为265,
故答案为:265.
12.【解析】令y=8,即y=-140x2+10=8,
解得:x=±45,
∴则EF=45-(﹣45)=85.
13.【解析】y=﹣3x2+36x=﹣3(x﹣6)2+108,
∴x=6(秒)时,汽车静止,此时滑行了108(米),
故当x=4(秒)时,y=﹣3x2+36x=96(米),
故汽车静止前2秒内滑行的距离是108﹣96=12(米),
故答案为12.
14.【解析】根据题意知,抛物线y=ax2+bx+c(a≠0)经过点(0,54.0)、(40,46.2)、(20,57.9),
则c=54.01600a+40b+c=46.2400a+20b+c=57.9,
解得:a=-0.0195b=0.585c=54.0,
所以x=-b2a=-0.5852×(-0.0195)=15(m).
故答案为:15.
15.【解析】建立如图所示的平面直角坐标系.
由题意可知各点的坐标,A(﹣4,0),B(4,0),D(﹣3,4).
设抛物线的解析式为:y=ax2+c(a≠0),把B(4,0),D(﹣3,4)代入,得
16a+c=09a+c=4,
解得a=-47c=647,
∴该抛物线的解析式为:y=-47x2+647,
则C(0,647).
∵647m≈9.1m.
故答案为:9.1.
16.【解析】设抛物线的表达式为:y=a(x﹣h)2+k=a(x﹣3)2+5,
将点(9,0)代入上式并解得:a=-536,
故抛物线的表达式为:y=-536(x﹣3)2+5,
令x=0,则y=154,即OA=154,
故答案为154.
17.【解析】以池中心为原点,竖直安装的水管为y轴,与水管垂直的为x轴建立直角坐标系.
由于在距池中心的水平距离为1m时达到最高,高度为3m,
则设抛物线的解析式为:y=a(x﹣1)2+3,
代入(3,0)求得:a=-34(x﹣1)2+3.
将a值代入得到抛物线的解析式为:y=-34(x﹣1)2+3(0≤x≤3);
令x=0,则y=-34+3=2.25.
故水管AB的长为2.25m.
故答案为:2.25.
18.【解析】设y轴右侧的抛物线解析式为:y=a(x﹣1)2+2.25
∵点A(0,1.25)在抛物线上
∴1.25=a(0﹣1)2+2.25
解得:a=﹣1
∴抛物线的解析式为:y=﹣(x﹣1)2+2.25
令y=0得:0=﹣(x﹣1)2+2.25
解得:x=2.5或x=﹣0.5(舍去)
∴点B坐标为(﹣2.5,0)
∴OB=OC=2.5
∴CB=5
故答案为:5.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解析】(1)如图,以AA1所在直线为x轴,以线段AA1的中点为坐标原点建立平面直角坐标系,
根据题意得A(﹣8,0),B(﹣8,6),C(0,8),
设抛物线的解析式为y=ax2+8,把B(﹣8,6)代入,得:
64a+8=6,
解得:a=-132.
∴抛物线的解析式为y=-132x2+8.
(2)根据题意,把x=±4代入解析式y=-132x2+8,
得y=7.5m.
∵7.5m>7m,
∴货运卡车能通过.
20.【解析】设抛物线的解析式为y=a(x﹣h)2+k,
根据题意得:抛物线的顶点坐标为(15,45),
∴y=a(x﹣15)2+45,
∵与x轴交于点A(60,0),
∴0=a(60﹣15)2+45,
解得:a=-145,
∴解析式为y=-145(x﹣15)2+45,
令x=0得:y=-145(0﹣15)2+45=40,
∴点B的坐标为(0,40),
∴这名运动员起跳时的竖直高度为40米.
21.【解析】(1)由题意可知,抛物线的顶点坐标(4,6),
设抛物线的方程为y=a(x﹣4)2+6,
又因为点A(0,2)在抛物线上,
所以有2=a(0﹣4)2+6.
所以a=-14.
因此有:y=-14(x-4)2+6;
(2)令y=4,则有4=-14(x-4)2+6,
解得:x1=4+22,x2=4-22,|x1-x2|=42>3,
∴货车可以通过.
22.【解析】(1)将点B、C的坐标代入抛物线表达式得:245=-45+2b+c215=-5+5b+c,解得b=65c=165,
故抛物线的表达式为:y=-15x2+65x+165;
(2)y=-15x2+65x+165,
令y=0,解得:x=﹣2(舍去)或8,
故ON=8;
(3)设点E(x,-15x2+65x+165),
由题意得:GE+EF=x-15x2+65x+165=-15(x-112)2+374
∵-15<0,
∴GE+EF的最大值为374,
∵374<10,
故现有库存10米的钢材够用.
23.【解析】(1)由题意得:函数y=at2+5t+c的图象经过(0,0.5)(0.8,3.5),
∴0.5=c3.5=0.82a+5×0.8+c,
解得:a=-2516c=12,
∴抛物线的解析式为:y=-2516t2+5t+12,
故答案为:-2516,12;
(2)∵y=-2516t2+5t+12,
∴y=-2516(t-85)2+92,
∴当t=85时,y最大=4.5,
∴当足球飞行的时间85s时,足球离地面最高,最大高度是4.5m;
(3)把x=28代入x=10t得t=2.8,
∴当t=2.8时,y=-2516×2.82+5×2.8+12=2.25<2.44,
∴他能将球直接射入球门.
24.【解析】(1)设抛物线的表达式为:y=a(x﹣7)2+2.88,
将x=0,y=1.9代入上式并解得:a=-150,
故抛物线的表达式为:y=-150(x﹣7)2+2.88;
当x=9时,y=-150(x﹣7)2+2.88=2.8>2.24,
当x=18时,y=-150(x﹣7)2+2.88=0.46>0,
故这次发球过网,但是出界了;
(2)如图,分别过点O,P作边线的平行线交于点Q,
在Rt△OPQ中,OQ=18﹣1=17,
当y=0时,-150(x﹣7)2+2.88=0,解得:x=19或﹣5(舍去﹣5),
∴OP=19,而OQ=17,
故PQ=62=8.4,
∵9﹣8.4﹣0.5=0.1,
∴发球点O在底线上且距右边线0.1米处.
