2.9二次函数与一元二次方程同步练习(含解析)
文档属性
| 名称 | 2.9二次函数与一元二次方程同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 16:55:53 | ||
图片预览




文档简介
2.9二次函数与一元二次方程
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,其中选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2019?碑林区校级模拟)下列关于二次函数y=ax2﹣(a+1)x+1(a>0)的图象经判断正确的是( )
A.对称轴位于y轴右侧
B.与x轴的交点有两个
C.当x>0时,y随x的增大而增大
D.与坐标轴的交点有三个
2.(2019秋?天等县期中)二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法错误的是( )
A.函数有最小值
B.对称轴是直线x=12
C.当x=﹣1或x=2时,y=0
D.当x>0时,y随x的增大而增大
3.(2020春?越秀区校级月考)抛物线y=x2+bx+3的对称轴为直线x=2.若关于x的一元二次方程x2+bx+3﹣t=0(t为实数)在﹣1<x<4的范围内有实数根,则t的取值范围是( )
A.﹣1≤t<3 B.3<t<8 C.﹣1≤t<8 D.﹣1<t<4
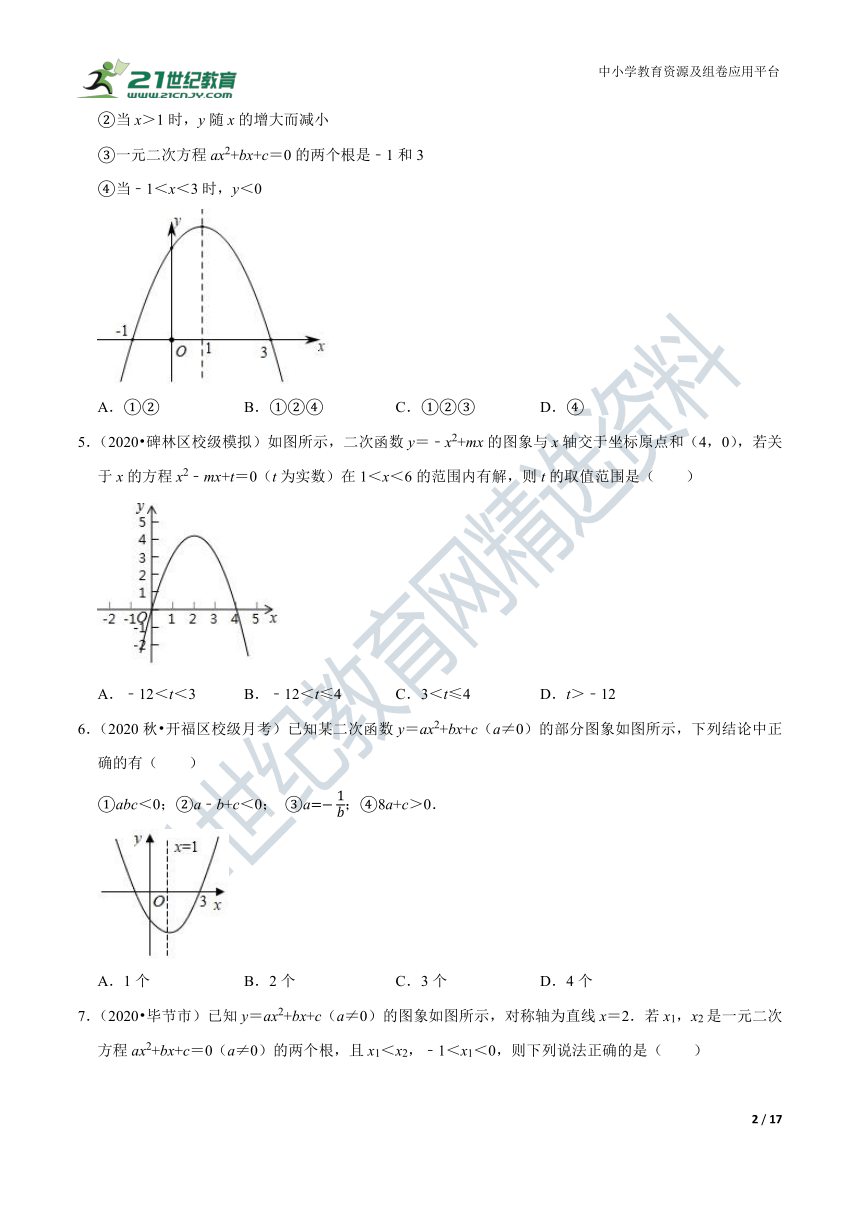
4.如图,抛物线y=ax2+bx+c交x轴于(﹣1,0),(3,0)两点:则下列判断中正确的是( )
①图象的对称轴是过点(1,0)且平行于y轴的直线
②当x>1时,y随x的增大而减小
③一元二次方程ax2+bx+c=0的两个根是﹣1和3
④当﹣1<x<3时,y<0
A.①② B.①②④ C.①②③ D.④
5.(2020?碑林区校级模拟)如图所示,二次函数y=﹣x2+mx的图象与x轴交于坐标原点和(4,0),若关于x的方程x2﹣mx+t=0(t为实数)在1<x<6的范围内有解,则t的取值范围是( )
A.﹣12<t<3 B.﹣12<t≤4 C.3<t≤4 D.t>﹣12
6.(2020秋?开福区校级月考)已知某二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,下列结论中正确的有( )
①abc<0;②a﹣b+c<0; ③a=-1b;④8a+c>0.
A.1个 B.2个 C.3个 D.4个
7.(2020?毕节市)已知y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=2.若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两个根,且x1<x2,﹣1<x1<0,则下列说法正确的是( )
A.x1+x2<0 B.4<x2<5 C.b2﹣4ac<0 D.ab>0
8.(2020?雁塔区校级模拟)已知二次函数y=ax2+bx+c的y与x的部分对应值如表:
x
﹣1
0
1
3
y
﹣3
1
3
1
下列结论:①抛物线的开口向下;②其图象的对称轴为直线x=1;③当x<2时,函数值y随x的增大而增大;④方程ax2+bx+c=0有一个根大于4.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
9.(2020秋?椒江区校级月考)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②4a+2b+c>0;③(a+c)2>b2;④2c<3b;⑤a+b>m(am+b)(m≠1的实数).其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
10.(2020?思明区校级模拟)二次函数y=x2+mx﹣n的对称轴为x=2.若关于x的一元二次方程x2+mx﹣n=0在﹣1<x<6的范围内有实数解,则n的取值范围是( )
A.﹣4≤n<5 B.n≥﹣4 C.﹣4≤n<12 D.5<n<12
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020?宁夏)若二次函数y=﹣x2+2x+k的图象与x轴有两个交点,则k的取值范围是 .
12.(2020春?岳麓区校级期末)抛物线y=﹣x2+bx+c的部分图象如图所示,则抛物线与x轴的另一个交点坐标为 .
13.(2019秋?西城区校级月考)如果函数y=x2+4x﹣m的图象与x轴有公共点,那么m的取值范围是 .
14.(2020?朝阳)抛物线y=(k﹣1)x2﹣x+1与x轴有交点,则k的取值范围是 .
15.(2020?东莞市校级模拟)已知抛物线y=x2+bx+c的部分图象如图所示,当y<0时,x的取值范围是 .
16.(2020?武汉模拟)抛物线y=ax2+bx+c经过A(﹣1,3),B(2,3),则关于x的一元二次方程a(x﹣2)2﹣3=2b﹣bx﹣c的解为 .
17.(2019秋?长春月考)如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,对称轴为直线x=12,抛物线与x轴的交点分别为A、B,则A、B两点间的距离是 .
18.(2018秋?安陆市期中)如图,一段抛物线y=﹣x2+4(﹣2≤x≤2)为C1,与x轴交于A0,A1两点,顶点为D1;将C1绕点A1旋转180°得到C2,顶点为D2;C1与C2组成一个新的图象,垂直于y轴的直线l与新图象交于点P1(x1,y1),P2(x2,y2),与线段D1D2交于点P3(x3,y3),设x1,x2,x3均为正数,t=x1+x2+x3,则t的取值范围是 .
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020秋?庆阳期中)已知抛物线y=x2﹣x﹣6与x轴交于A,B两点(点A在点B的左侧),与y轴交于C点.
(1)求点A,B,C的坐标;
(2)若P(m,﹣4)为二次函数y=x2﹣x﹣6图象上一点,求m的值.
20.(2020秋?南开区期中)如图,已知抛物线y=﹣x2+(m﹣1)x+m的对称轴为x=1,请你解答下列问题:
(Ⅰ)求m的值;
(Ⅱ)求出抛物线与x轴的交点;
(Ⅲ)当y随x的增大而减小时x的取值范围是 .
(Ⅳ)当y<0时,x的取值范围是 .
21.(2019秋?龙湾区期中)已知函数y=x2+(m+3)x+2m+2
(1)判断该函数的图象与x轴的交点个数.
(2)若m=﹣5,求出函数值y在0<x<5时的取值范围.
(3)若方程x2﹣2x﹣8=k在0<x<5内有且只有一个解,直接写出k的范围.
22.(2020?岳麓区校级二模)已知二次函数y=ax2+bx+c(a≠0).
(1)若b=1,a=-12c,求证:二次函数的图象与x轴一定有两个不同的交点;
(2)若a<0,c=0,且对于任意的实数x,都有y≤1,求4a+b2的取值范围;
(3)若函数图象上两点(0,y1)和(1,y2)满足y1?y2>0,且2a+3b+6c=0,试确定二次函数图象对称轴与x轴交点横坐标的取值范围.
23.(2020?南通)已知抛物线y=ax2+bx+c经过A(2,0),B(3n﹣4,y1),C(5n+6,y2)三点,对称轴是直线x=1.关于x的方程ax2+bx+c=x有两个相等的实数根.
(1)求抛物线的解析式;
(2)若n<﹣5,试比较y1与y2的大小;
(3)若B,C两点在直线x=1的两侧,且y1>y2,求n的取值范围.
24.(2020秋?海淀区期中)如图,在平面直角坐标系xOy中,一次函数y=﹣x+m的图象过点A(1,3),且与x轴交于点B.
(1)求m的值和点B的坐标;
(2)若二次函数y=ax2+bx图象过A,B两点,直接写出关于x的不等式ax2+bx>﹣x+m的解集.
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解析】A.∵a>0,
∴对称轴为x=-a+12a<0,
∴对称轴位于y轴左边,
故A错误,不符合题意;
B.∵△=(a+1)2﹣4a=a2+2a+1﹣4a=(a﹣1)2,
∴当a=1时,△=0,
∴当a=1时,抛物线与x轴只一个交点,
故B错误,不符合题意;
C.由A知,对称轴位于y轴左边,抛物线开口向上,
则函数对称轴右侧y随x的增大而增大,
故当x>0时,y随x的增大而增大,正确,符合题意;
D.由B知,当a=1时,抛物线与x轴只一个交点,此时抛物线与坐标轴就没有三个交点,
故D错误,不符合题意;
故选:C.
2.【解析】由函数图象可得,
函数y=ax2+bx+c(a≠0)有最小值,故选项A正确;
对称轴是直线x=-1+22=12,故选项B正确;
当x=﹣1或x=2时,y=0,故选项C正确;
当0<x<12时,y随x的增大而减小,故选项D错误;
故选:D.
3.【解析】∵抛物线y=x2+bx+3的对称轴为直线x=2.
∴-b2=2,解得:b=﹣4,
∴y=x2﹣4x+3,
∴一元二次方程x2+bx+3﹣t=0有实数根可以看做y=x2﹣4x+3与函数y=t有交点,
∵方程x2﹣4x+3﹣t=0(t为实数)在﹣1<x<4的范围内只有一个实数根,
当x=﹣1时,y=8;
当x=4时,y=3;
当x=2时,y=﹣1;
∴t的取值范围是﹣1≤t<8.
故选:C.
4.【解析】二次函数的图象与x轴的交点为(﹣1,0),(3,0),
抛物线的对称轴直线为:x=3-12=1,故①正确;
∵抛物线开口向下,对称轴为x=1,
∴当x>1时,y随x的增大而减小,故②正确;
∵二次函数的图象与x轴的交点为(﹣1,0),(3,0),
∴一元二次方程的两个根是﹣1,3,故③正确;
∵当﹣1<x<3时,抛物线在x轴的上方,
∴当﹣1<x<3时,y>0,故④错误.
综上,正确的选项有①②③.
故选:C.
5.【解析】∵抛物线的对称轴为直线x=-m2×(-1)=2,解得m=4,
∴抛物线解析式为y=﹣x2+4x,
抛物线的顶点坐标为(2,4),
当x=1时,y=﹣x2+4x=﹣1+4=3;
当x=6时,y=﹣x2+4x=﹣36+24=﹣12,
当x=2时,y=4,
在1<x<6时有公共点时
当直线y=t与抛物线y=﹣x2+4x在1<x<6时有公共点时,﹣12<t≤4,
故选:B.
6.【解析】①函数的对称轴在y轴右侧,则ab<0,而c<0,则abc>0,故①错误;
②函数的对称轴为x=1,函数和x轴的一个交点是(3,0),则另外一个交点为(﹣1,0),
当x=﹣1时,y=a﹣b+c=0,故②错误;
③函数的对称轴为x=-b2a=1,即a=-12b,故③错误;
④由②③得,b=﹣2a,a﹣b+c=0,故3a+c=0,而a>0,即5a>0,故8a+c>0,故④正确;
故选:A.
7.【解析】∵x1,x2是一元二次方程ax2+bx+c=0的两个根,
∴x1、x2是抛物线与x轴交点的横坐标,
∵抛物线的对称轴为直线x=2,
∴x1+x22=2,即x1+x2=4>0,故选项A错误;
∵x1<x2,﹣1<x1<0,
∴﹣1<4﹣x2<0,
解得:4<x2<5,故选项B正确;
∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,故选项C错误;
∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=2,
∴-b2a=2,
∴b=﹣4a>0,
∴ab<0,故选项D错误;
故选:B.
8.【解析】根据题意:将点(﹣1,﹣3)、(0,1)、(1,3)代入二次函数y=ax2+bx+c中,
a-b+c=-3c=1a+b+c=3,
解得a=-1b=3c=1,
所以二次函数y=﹣x2+3x+1,
∵a=﹣1<0,
∴抛物线的开口向下,
所以①正确;
∵y=﹣x2+3x+1=﹣(x-32)2+134,
则图象的对称轴为直线x=32,
所以②错误;
∵图象的对称轴为直线x=32,
∴当x<32时,函数值y随x的增大而增大,
所以③错误;
当y=0时,﹣(x-32)2+134=0,
解得x1=3-132,x2=3+132,
∵3<13<4,
∴3<3+132<72,
所以方程ax2+bx+c=0有一个根小于4,
所以④错误.
综上所述:其中正确的结论有①.
故选:A.
9.【解析】①由图象可知:a<0,c>0,
∵-b2a>0,
∴b>0,
∴abc<0,故此选项错误;
②由对称知,当x=2时,函数值大于0,即y=4a+2b+c>0,故此选项正确;
③当x=﹣1时,y=a﹣b+c<0;当x=1时,y=a+b+c>0,
∴(a﹣b+c)(a+b+c)<0,即(a+c)2﹣b2<0,
∴(a+c)2<b2,故此选项错误;
④当x=3时函数值小于0,y=9a+3b+c<0,且x=-b2a=1,
即a=-b2,代入得9(-b2)+3b+c<0,得2c<3b,故此选项正确;
⑤当x=1时,y的值最大.此时,y=a+b+c,
而当x=m时,y=am2+bm+c,
所以a+b+c>am2+bm+c,
故a+b>am2+bm,即a+b>m(am+b),故此选项正确.
故②④⑤正确.
故选:B.
10.【解析】∵抛物线的对称轴x=-m2=2,
∴m=﹣4,
则方程x2+mx﹣n=0,即x2﹣4x﹣n=0的解相当于y=x2﹣4x与直线y=n的交点的横坐标,
∵方程x2+mx﹣n=0在﹣1<x<6的范围内有实数解,
∴当x=﹣1时,y=1+4=5,
当x=6时,y=36﹣24=12,
又∵y=x2﹣4x=(x﹣2)2﹣4,
∴当﹣4≤n<12时,在﹣1<x<6的范围内有解.
∴n的取值范围是﹣4≤n<12,
故选:C.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解析】∵二次函数y=﹣x2+2x+k的图象与x轴有两个交点,
∴△=4﹣4×(﹣1)?k>0,
解得:k>﹣1,
故答案为:k>﹣1.
12.【解析】如图,抛物线的对称轴为直线x=﹣1,根据抛物线的对称性,可得抛物线与x轴两交点到对称轴的距离相等,那么抛物线与x轴的另一个交点的横坐标为﹣3,纵坐标为0,则抛物线与x轴的另一个交点坐标为(﹣3,0).
故答案是:(﹣3,0).
13.【解析】∵函数y=x2+4x﹣m的图象与x轴有公共点,
∴△=42﹣4×1×(﹣m)≥0,
∴m≥﹣4.
故答案为:m≥﹣4.
14.【解析】∵抛物线y=(k﹣1)x2﹣x+1与x轴有交点,
∴△=(﹣1)2﹣4×(k﹣1)×1≥0,解得k≤54,
又∵k﹣1≠0,
∴k≠1,
∴k的取值范围是k≤54且k≠1;
故答案为:k≤54且k≠1.
15.【解析】由图象可得,
该抛物线的对称轴为直线x=1,与x轴的一个交点为(﹣1,0),
故抛物线与x轴的另一个交点为(3,0),
故当y<0时,x的取值范围是﹣1<x<3.
16.【解答】关于x的一元二次方程a(x﹣2)2+bx=2b﹣c变形为a(x﹣2)2+b(x﹣2)+c=0,
把抛物线y=ax2+bx+c沿x轴向右平移2个单位得到y′=a(x﹣2)2+b(x﹣2)+c,
设y′′=3,
当y′=y′′时,即a(x﹣2)2+b(x﹣2)+c=3,即a(x﹣2)2﹣3=2b﹣bx﹣c,
即一元二次方程a(x﹣2)2﹣3=2b﹣bx﹣c的解转化为y′=y′′的交点,
而平移前函数交点的横坐标为﹣1或2,向右平移2个单位后交点的横坐标为1或4
故答案为1或4.
17.【解析】由图象可知,
该抛物线的对称轴是直线x=12,与x轴的一个交点是(2,0),则与x轴的另一个交点为(﹣1,0),
设点A(﹣1,0),则点B为(2,0),
故AB=2﹣(﹣1)=2+1=3,
故答案为:3.
18.【解析】当﹣x2+4=0,解得x1=﹣2,x2=2,则A0(﹣2,0),A1(2,0),
抛物线y=﹣x2+4的顶点为D1的坐标为(0,4),
∵将C1绕点A1旋转180°得到C2,顶点为D2;
∴D2的坐标为(4,﹣4),
抛物线C2的对称轴为直线x=4,
∵x2﹣4=4﹣x1,
∴x1+x2=8,
∵点P3(x3,y3)在线段A1D2上,x1,x2,x3均为正数,
∴2≤x3≤4,
∴10≤x1+x2+x3≤12,即10≤t≤12.
故答案为10≤t≤12.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解析】(1)对于y=x2﹣x﹣6,令y=x2﹣x﹣6=0,解得x=3或﹣2,令x=0,则y=﹣6,
故点A、B、C的坐标分别为(3,0)、(﹣2,0)、(0,﹣6)
(2)将点P的坐标代入y=x2﹣x﹣6得,﹣4=m2﹣m﹣6,解得m=2或﹣1.
20.【解析】(Ⅰ)抛物线的对称轴为直线x=-m-12×(-1)=1,
∴m=3;
(Ⅱ)∵m=3,
∴抛物线解析式为y=﹣x2+2x+3,
当y=0时,﹣x2+2x+3=0,解得x1=﹣1,x2=3,
∴抛物线与x轴的交点为(﹣1,0),(3,0);
(Ⅲ)∵a=﹣1<0,对称轴为直线x=1,
∴当x>1时,y的值随x的增大而减小,
故答案为x>1;
(Ⅳ)当x<﹣1或x>3时,y<0,
故答案为x<﹣1或x>3.
21.【解析】(1)∵△=(m+3)2﹣4(2m+2)=m2﹣2m+1=(m﹣1)2,
∴当m=1时,图象与x轴只有一个交点,当m≠1时,图象与x轴有两个交点;
(2)m=﹣5时,y=x2﹣2x﹣8=(x﹣1)2﹣9,
当x=1时,函数有最小值﹣9,
当x=5时,y=7,
故:﹣9≤y<7;
(3)若方程x2﹣2x﹣8=k在0<x<5内有且只有一个解,
即为y=x2﹣2x﹣8和函数y=k只有一个交点,
函数y=x2﹣2x﹣8,与y轴的交点为:(0,﹣8),函数的顶点坐标为:(1,﹣9),
故在0<x<5时,
y=x2﹣2x﹣8和函数y=k只有一个交点时,k=﹣9或﹣8≤k<7.
22.【解析】(1)证明:∵y=ax2+bx+c(a≠0),
∴令y=0得:ax2+bx+c=0
∵b=1,a=-12c,
∴△=b2﹣4ac=1﹣4(-12c)c=1+2c2,
∵2c2≥0,
∴1+2c2>0,即△>0,
∴二次函数的图象与x轴一定有两个不同的交点;
(2)∵a<0,c=0,
∴抛物线的解析式为y=ax2+bx,其图象开口向下,
又∵对于任意的实数x,都有y≤1,
∴顶点纵坐标-b24a≤1,
∴﹣b2≥4a,
∴4a+b2≤0;
(3)由2a+3b+6c=0,可得6c=﹣(2a+3b),
∵函数图象上两点(0,y1)和(1,y2)满足y1?y2>0,
∴c(a+b+c)>0,
∴6c(6a+6b+6c)>0,
∴将6c=﹣(2a+3b)代入上式得,﹣(2a+3b)(4a+3b)>0,
∴(2a+3b)(4a+3b)<0,
∵a≠0,则9a2>0,
∴两边同除以9a2得,
(ba+23)(ba+43)<0,
∴ba+23<0ba+43>0或ba+23>0ba+43<0,
∴-43<ba<-23,
∴二次函数图象对称轴与x轴交点横坐标的取值范围是13<-b2a<23.
23.【解析】(1)∵抛物线y=ax2+bx+c经过A(2,0),
∴0=4a+2b+c①,
∵对称轴是直线x=1,
∴-b2a=1②,
∵关于x的方程ax2+bx+c=x有两个相等的实数根,
∴△=(b﹣1)2﹣4ac=0③,
由①②③可得:a=-12b=1c=0,
∴抛物线的解析式为y=-12x2+x;
(2)∵n<﹣5,
∴3n﹣4<﹣19,5n+6<﹣19
∴点B,点C在对称轴直线x=1的左侧,
∵抛物线y=-12x2+x,
∴-12<0,即y随x的增大而增大,
∵(3n﹣4)﹣(5n+6)=﹣2n﹣10=﹣2(n+5)>0,
∴3n﹣4>5n+6,
∴y1>y2;
(3)若点B在对称轴直线x=1的左侧,点C在对称轴直线x=1的右侧时,
由题意可得3n-4<15n+6>11-(3n-4)<5n+6-1,
∴0<n<53,
若点C在对称轴直线x=1的左侧,点B在对称轴直线x=1的右侧时,
由题意可得:3n-4>15n+6<13n-4-1<1-(5n+6),
∴不等式组无解,
综上所述:0<n<53.
24.【解析】(1)∵一次函数y=﹣x+m的图象过点A(1,3),
∴3=﹣1+m,
∴m=4,
∴一次函数为y=﹣x+4,
令y=0,得x=4,
∴点B的坐标为(4,0);
(2)∵二次函数y=ax2+bx图象过A,B两点,
∴a+b=316a+b=0,解得a=-13,
∴抛物线开口向下,
∴不等式ax2+bx>﹣x+m的解集为1<x<4.
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,其中选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2019?碑林区校级模拟)下列关于二次函数y=ax2﹣(a+1)x+1(a>0)的图象经判断正确的是( )
A.对称轴位于y轴右侧
B.与x轴的交点有两个
C.当x>0时,y随x的增大而增大
D.与坐标轴的交点有三个
2.(2019秋?天等县期中)二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法错误的是( )
A.函数有最小值
B.对称轴是直线x=12
C.当x=﹣1或x=2时,y=0
D.当x>0时,y随x的增大而增大
3.(2020春?越秀区校级月考)抛物线y=x2+bx+3的对称轴为直线x=2.若关于x的一元二次方程x2+bx+3﹣t=0(t为实数)在﹣1<x<4的范围内有实数根,则t的取值范围是( )
A.﹣1≤t<3 B.3<t<8 C.﹣1≤t<8 D.﹣1<t<4
4.如图,抛物线y=ax2+bx+c交x轴于(﹣1,0),(3,0)两点:则下列判断中正确的是( )
①图象的对称轴是过点(1,0)且平行于y轴的直线
②当x>1时,y随x的增大而减小
③一元二次方程ax2+bx+c=0的两个根是﹣1和3
④当﹣1<x<3时,y<0
A.①② B.①②④ C.①②③ D.④
5.(2020?碑林区校级模拟)如图所示,二次函数y=﹣x2+mx的图象与x轴交于坐标原点和(4,0),若关于x的方程x2﹣mx+t=0(t为实数)在1<x<6的范围内有解,则t的取值范围是( )
A.﹣12<t<3 B.﹣12<t≤4 C.3<t≤4 D.t>﹣12
6.(2020秋?开福区校级月考)已知某二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,下列结论中正确的有( )
①abc<0;②a﹣b+c<0; ③a=-1b;④8a+c>0.
A.1个 B.2个 C.3个 D.4个
7.(2020?毕节市)已知y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=2.若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两个根,且x1<x2,﹣1<x1<0,则下列说法正确的是( )
A.x1+x2<0 B.4<x2<5 C.b2﹣4ac<0 D.ab>0
8.(2020?雁塔区校级模拟)已知二次函数y=ax2+bx+c的y与x的部分对应值如表:
x
﹣1
0
1
3
y
﹣3
1
3
1
下列结论:①抛物线的开口向下;②其图象的对称轴为直线x=1;③当x<2时,函数值y随x的增大而增大;④方程ax2+bx+c=0有一个根大于4.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
9.(2020秋?椒江区校级月考)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②4a+2b+c>0;③(a+c)2>b2;④2c<3b;⑤a+b>m(am+b)(m≠1的实数).其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
10.(2020?思明区校级模拟)二次函数y=x2+mx﹣n的对称轴为x=2.若关于x的一元二次方程x2+mx﹣n=0在﹣1<x<6的范围内有实数解,则n的取值范围是( )
A.﹣4≤n<5 B.n≥﹣4 C.﹣4≤n<12 D.5<n<12
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020?宁夏)若二次函数y=﹣x2+2x+k的图象与x轴有两个交点,则k的取值范围是 .
12.(2020春?岳麓区校级期末)抛物线y=﹣x2+bx+c的部分图象如图所示,则抛物线与x轴的另一个交点坐标为 .
13.(2019秋?西城区校级月考)如果函数y=x2+4x﹣m的图象与x轴有公共点,那么m的取值范围是 .
14.(2020?朝阳)抛物线y=(k﹣1)x2﹣x+1与x轴有交点,则k的取值范围是 .
15.(2020?东莞市校级模拟)已知抛物线y=x2+bx+c的部分图象如图所示,当y<0时,x的取值范围是 .
16.(2020?武汉模拟)抛物线y=ax2+bx+c经过A(﹣1,3),B(2,3),则关于x的一元二次方程a(x﹣2)2﹣3=2b﹣bx﹣c的解为 .
17.(2019秋?长春月考)如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,对称轴为直线x=12,抛物线与x轴的交点分别为A、B,则A、B两点间的距离是 .
18.(2018秋?安陆市期中)如图,一段抛物线y=﹣x2+4(﹣2≤x≤2)为C1,与x轴交于A0,A1两点,顶点为D1;将C1绕点A1旋转180°得到C2,顶点为D2;C1与C2组成一个新的图象,垂直于y轴的直线l与新图象交于点P1(x1,y1),P2(x2,y2),与线段D1D2交于点P3(x3,y3),设x1,x2,x3均为正数,t=x1+x2+x3,则t的取值范围是 .
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020秋?庆阳期中)已知抛物线y=x2﹣x﹣6与x轴交于A,B两点(点A在点B的左侧),与y轴交于C点.
(1)求点A,B,C的坐标;
(2)若P(m,﹣4)为二次函数y=x2﹣x﹣6图象上一点,求m的值.
20.(2020秋?南开区期中)如图,已知抛物线y=﹣x2+(m﹣1)x+m的对称轴为x=1,请你解答下列问题:
(Ⅰ)求m的值;
(Ⅱ)求出抛物线与x轴的交点;
(Ⅲ)当y随x的增大而减小时x的取值范围是 .
(Ⅳ)当y<0时,x的取值范围是 .
21.(2019秋?龙湾区期中)已知函数y=x2+(m+3)x+2m+2
(1)判断该函数的图象与x轴的交点个数.
(2)若m=﹣5,求出函数值y在0<x<5时的取值范围.
(3)若方程x2﹣2x﹣8=k在0<x<5内有且只有一个解,直接写出k的范围.
22.(2020?岳麓区校级二模)已知二次函数y=ax2+bx+c(a≠0).
(1)若b=1,a=-12c,求证:二次函数的图象与x轴一定有两个不同的交点;
(2)若a<0,c=0,且对于任意的实数x,都有y≤1,求4a+b2的取值范围;
(3)若函数图象上两点(0,y1)和(1,y2)满足y1?y2>0,且2a+3b+6c=0,试确定二次函数图象对称轴与x轴交点横坐标的取值范围.
23.(2020?南通)已知抛物线y=ax2+bx+c经过A(2,0),B(3n﹣4,y1),C(5n+6,y2)三点,对称轴是直线x=1.关于x的方程ax2+bx+c=x有两个相等的实数根.
(1)求抛物线的解析式;
(2)若n<﹣5,试比较y1与y2的大小;
(3)若B,C两点在直线x=1的两侧,且y1>y2,求n的取值范围.
24.(2020秋?海淀区期中)如图,在平面直角坐标系xOy中,一次函数y=﹣x+m的图象过点A(1,3),且与x轴交于点B.
(1)求m的值和点B的坐标;
(2)若二次函数y=ax2+bx图象过A,B两点,直接写出关于x的不等式ax2+bx>﹣x+m的解集.
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解析】A.∵a>0,
∴对称轴为x=-a+12a<0,
∴对称轴位于y轴左边,
故A错误,不符合题意;
B.∵△=(a+1)2﹣4a=a2+2a+1﹣4a=(a﹣1)2,
∴当a=1时,△=0,
∴当a=1时,抛物线与x轴只一个交点,
故B错误,不符合题意;
C.由A知,对称轴位于y轴左边,抛物线开口向上,
则函数对称轴右侧y随x的增大而增大,
故当x>0时,y随x的增大而增大,正确,符合题意;
D.由B知,当a=1时,抛物线与x轴只一个交点,此时抛物线与坐标轴就没有三个交点,
故D错误,不符合题意;
故选:C.
2.【解析】由函数图象可得,
函数y=ax2+bx+c(a≠0)有最小值,故选项A正确;
对称轴是直线x=-1+22=12,故选项B正确;
当x=﹣1或x=2时,y=0,故选项C正确;
当0<x<12时,y随x的增大而减小,故选项D错误;
故选:D.
3.【解析】∵抛物线y=x2+bx+3的对称轴为直线x=2.
∴-b2=2,解得:b=﹣4,
∴y=x2﹣4x+3,
∴一元二次方程x2+bx+3﹣t=0有实数根可以看做y=x2﹣4x+3与函数y=t有交点,
∵方程x2﹣4x+3﹣t=0(t为实数)在﹣1<x<4的范围内只有一个实数根,
当x=﹣1时,y=8;
当x=4时,y=3;
当x=2时,y=﹣1;
∴t的取值范围是﹣1≤t<8.
故选:C.
4.【解析】二次函数的图象与x轴的交点为(﹣1,0),(3,0),
抛物线的对称轴直线为:x=3-12=1,故①正确;
∵抛物线开口向下,对称轴为x=1,
∴当x>1时,y随x的增大而减小,故②正确;
∵二次函数的图象与x轴的交点为(﹣1,0),(3,0),
∴一元二次方程的两个根是﹣1,3,故③正确;
∵当﹣1<x<3时,抛物线在x轴的上方,
∴当﹣1<x<3时,y>0,故④错误.
综上,正确的选项有①②③.
故选:C.
5.【解析】∵抛物线的对称轴为直线x=-m2×(-1)=2,解得m=4,
∴抛物线解析式为y=﹣x2+4x,
抛物线的顶点坐标为(2,4),
当x=1时,y=﹣x2+4x=﹣1+4=3;
当x=6时,y=﹣x2+4x=﹣36+24=﹣12,
当x=2时,y=4,
在1<x<6时有公共点时
当直线y=t与抛物线y=﹣x2+4x在1<x<6时有公共点时,﹣12<t≤4,
故选:B.
6.【解析】①函数的对称轴在y轴右侧,则ab<0,而c<0,则abc>0,故①错误;
②函数的对称轴为x=1,函数和x轴的一个交点是(3,0),则另外一个交点为(﹣1,0),
当x=﹣1时,y=a﹣b+c=0,故②错误;
③函数的对称轴为x=-b2a=1,即a=-12b,故③错误;
④由②③得,b=﹣2a,a﹣b+c=0,故3a+c=0,而a>0,即5a>0,故8a+c>0,故④正确;
故选:A.
7.【解析】∵x1,x2是一元二次方程ax2+bx+c=0的两个根,
∴x1、x2是抛物线与x轴交点的横坐标,
∵抛物线的对称轴为直线x=2,
∴x1+x22=2,即x1+x2=4>0,故选项A错误;
∵x1<x2,﹣1<x1<0,
∴﹣1<4﹣x2<0,
解得:4<x2<5,故选项B正确;
∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,故选项C错误;
∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=2,
∴-b2a=2,
∴b=﹣4a>0,
∴ab<0,故选项D错误;
故选:B.
8.【解析】根据题意:将点(﹣1,﹣3)、(0,1)、(1,3)代入二次函数y=ax2+bx+c中,
a-b+c=-3c=1a+b+c=3,
解得a=-1b=3c=1,
所以二次函数y=﹣x2+3x+1,
∵a=﹣1<0,
∴抛物线的开口向下,
所以①正确;
∵y=﹣x2+3x+1=﹣(x-32)2+134,
则图象的对称轴为直线x=32,
所以②错误;
∵图象的对称轴为直线x=32,
∴当x<32时,函数值y随x的增大而增大,
所以③错误;
当y=0时,﹣(x-32)2+134=0,
解得x1=3-132,x2=3+132,
∵3<13<4,
∴3<3+132<72,
所以方程ax2+bx+c=0有一个根小于4,
所以④错误.
综上所述:其中正确的结论有①.
故选:A.
9.【解析】①由图象可知:a<0,c>0,
∵-b2a>0,
∴b>0,
∴abc<0,故此选项错误;
②由对称知,当x=2时,函数值大于0,即y=4a+2b+c>0,故此选项正确;
③当x=﹣1时,y=a﹣b+c<0;当x=1时,y=a+b+c>0,
∴(a﹣b+c)(a+b+c)<0,即(a+c)2﹣b2<0,
∴(a+c)2<b2,故此选项错误;
④当x=3时函数值小于0,y=9a+3b+c<0,且x=-b2a=1,
即a=-b2,代入得9(-b2)+3b+c<0,得2c<3b,故此选项正确;
⑤当x=1时,y的值最大.此时,y=a+b+c,
而当x=m时,y=am2+bm+c,
所以a+b+c>am2+bm+c,
故a+b>am2+bm,即a+b>m(am+b),故此选项正确.
故②④⑤正确.
故选:B.
10.【解析】∵抛物线的对称轴x=-m2=2,
∴m=﹣4,
则方程x2+mx﹣n=0,即x2﹣4x﹣n=0的解相当于y=x2﹣4x与直线y=n的交点的横坐标,
∵方程x2+mx﹣n=0在﹣1<x<6的范围内有实数解,
∴当x=﹣1时,y=1+4=5,
当x=6时,y=36﹣24=12,
又∵y=x2﹣4x=(x﹣2)2﹣4,
∴当﹣4≤n<12时,在﹣1<x<6的范围内有解.
∴n的取值范围是﹣4≤n<12,
故选:C.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解析】∵二次函数y=﹣x2+2x+k的图象与x轴有两个交点,
∴△=4﹣4×(﹣1)?k>0,
解得:k>﹣1,
故答案为:k>﹣1.
12.【解析】如图,抛物线的对称轴为直线x=﹣1,根据抛物线的对称性,可得抛物线与x轴两交点到对称轴的距离相等,那么抛物线与x轴的另一个交点的横坐标为﹣3,纵坐标为0,则抛物线与x轴的另一个交点坐标为(﹣3,0).
故答案是:(﹣3,0).
13.【解析】∵函数y=x2+4x﹣m的图象与x轴有公共点,
∴△=42﹣4×1×(﹣m)≥0,
∴m≥﹣4.
故答案为:m≥﹣4.
14.【解析】∵抛物线y=(k﹣1)x2﹣x+1与x轴有交点,
∴△=(﹣1)2﹣4×(k﹣1)×1≥0,解得k≤54,
又∵k﹣1≠0,
∴k≠1,
∴k的取值范围是k≤54且k≠1;
故答案为:k≤54且k≠1.
15.【解析】由图象可得,
该抛物线的对称轴为直线x=1,与x轴的一个交点为(﹣1,0),
故抛物线与x轴的另一个交点为(3,0),
故当y<0时,x的取值范围是﹣1<x<3.
16.【解答】关于x的一元二次方程a(x﹣2)2+bx=2b﹣c变形为a(x﹣2)2+b(x﹣2)+c=0,
把抛物线y=ax2+bx+c沿x轴向右平移2个单位得到y′=a(x﹣2)2+b(x﹣2)+c,
设y′′=3,
当y′=y′′时,即a(x﹣2)2+b(x﹣2)+c=3,即a(x﹣2)2﹣3=2b﹣bx﹣c,
即一元二次方程a(x﹣2)2﹣3=2b﹣bx﹣c的解转化为y′=y′′的交点,
而平移前函数交点的横坐标为﹣1或2,向右平移2个单位后交点的横坐标为1或4
故答案为1或4.
17.【解析】由图象可知,
该抛物线的对称轴是直线x=12,与x轴的一个交点是(2,0),则与x轴的另一个交点为(﹣1,0),
设点A(﹣1,0),则点B为(2,0),
故AB=2﹣(﹣1)=2+1=3,
故答案为:3.
18.【解析】当﹣x2+4=0,解得x1=﹣2,x2=2,则A0(﹣2,0),A1(2,0),
抛物线y=﹣x2+4的顶点为D1的坐标为(0,4),
∵将C1绕点A1旋转180°得到C2,顶点为D2;
∴D2的坐标为(4,﹣4),
抛物线C2的对称轴为直线x=4,
∵x2﹣4=4﹣x1,
∴x1+x2=8,
∵点P3(x3,y3)在线段A1D2上,x1,x2,x3均为正数,
∴2≤x3≤4,
∴10≤x1+x2+x3≤12,即10≤t≤12.
故答案为10≤t≤12.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解析】(1)对于y=x2﹣x﹣6,令y=x2﹣x﹣6=0,解得x=3或﹣2,令x=0,则y=﹣6,
故点A、B、C的坐标分别为(3,0)、(﹣2,0)、(0,﹣6)
(2)将点P的坐标代入y=x2﹣x﹣6得,﹣4=m2﹣m﹣6,解得m=2或﹣1.
20.【解析】(Ⅰ)抛物线的对称轴为直线x=-m-12×(-1)=1,
∴m=3;
(Ⅱ)∵m=3,
∴抛物线解析式为y=﹣x2+2x+3,
当y=0时,﹣x2+2x+3=0,解得x1=﹣1,x2=3,
∴抛物线与x轴的交点为(﹣1,0),(3,0);
(Ⅲ)∵a=﹣1<0,对称轴为直线x=1,
∴当x>1时,y的值随x的增大而减小,
故答案为x>1;
(Ⅳ)当x<﹣1或x>3时,y<0,
故答案为x<﹣1或x>3.
21.【解析】(1)∵△=(m+3)2﹣4(2m+2)=m2﹣2m+1=(m﹣1)2,
∴当m=1时,图象与x轴只有一个交点,当m≠1时,图象与x轴有两个交点;
(2)m=﹣5时,y=x2﹣2x﹣8=(x﹣1)2﹣9,
当x=1时,函数有最小值﹣9,
当x=5时,y=7,
故:﹣9≤y<7;
(3)若方程x2﹣2x﹣8=k在0<x<5内有且只有一个解,
即为y=x2﹣2x﹣8和函数y=k只有一个交点,
函数y=x2﹣2x﹣8,与y轴的交点为:(0,﹣8),函数的顶点坐标为:(1,﹣9),
故在0<x<5时,
y=x2﹣2x﹣8和函数y=k只有一个交点时,k=﹣9或﹣8≤k<7.
22.【解析】(1)证明:∵y=ax2+bx+c(a≠0),
∴令y=0得:ax2+bx+c=0
∵b=1,a=-12c,
∴△=b2﹣4ac=1﹣4(-12c)c=1+2c2,
∵2c2≥0,
∴1+2c2>0,即△>0,
∴二次函数的图象与x轴一定有两个不同的交点;
(2)∵a<0,c=0,
∴抛物线的解析式为y=ax2+bx,其图象开口向下,
又∵对于任意的实数x,都有y≤1,
∴顶点纵坐标-b24a≤1,
∴﹣b2≥4a,
∴4a+b2≤0;
(3)由2a+3b+6c=0,可得6c=﹣(2a+3b),
∵函数图象上两点(0,y1)和(1,y2)满足y1?y2>0,
∴c(a+b+c)>0,
∴6c(6a+6b+6c)>0,
∴将6c=﹣(2a+3b)代入上式得,﹣(2a+3b)(4a+3b)>0,
∴(2a+3b)(4a+3b)<0,
∵a≠0,则9a2>0,
∴两边同除以9a2得,
(ba+23)(ba+43)<0,
∴ba+23<0ba+43>0或ba+23>0ba+43<0,
∴-43<ba<-23,
∴二次函数图象对称轴与x轴交点横坐标的取值范围是13<-b2a<23.
23.【解析】(1)∵抛物线y=ax2+bx+c经过A(2,0),
∴0=4a+2b+c①,
∵对称轴是直线x=1,
∴-b2a=1②,
∵关于x的方程ax2+bx+c=x有两个相等的实数根,
∴△=(b﹣1)2﹣4ac=0③,
由①②③可得:a=-12b=1c=0,
∴抛物线的解析式为y=-12x2+x;
(2)∵n<﹣5,
∴3n﹣4<﹣19,5n+6<﹣19
∴点B,点C在对称轴直线x=1的左侧,
∵抛物线y=-12x2+x,
∴-12<0,即y随x的增大而增大,
∵(3n﹣4)﹣(5n+6)=﹣2n﹣10=﹣2(n+5)>0,
∴3n﹣4>5n+6,
∴y1>y2;
(3)若点B在对称轴直线x=1的左侧,点C在对称轴直线x=1的右侧时,
由题意可得3n-4<15n+6>11-(3n-4)<5n+6-1,
∴0<n<53,
若点C在对称轴直线x=1的左侧,点B在对称轴直线x=1的右侧时,
由题意可得:3n-4>15n+6<13n-4-1<1-(5n+6),
∴不等式组无解,
综上所述:0<n<53.
24.【解析】(1)∵一次函数y=﹣x+m的图象过点A(1,3),
∴3=﹣1+m,
∴m=4,
∴一次函数为y=﹣x+4,
令y=0,得x=4,
∴点B的坐标为(4,0);
(2)∵二次函数y=ax2+bx图象过A,B两点,
∴a+b=316a+b=0,解得a=-13,
∴抛物线开口向下,
∴不等式ax2+bx>﹣x+m的解集为1<x<4.
