山西省运城市新绛县第二中学2021届高三上学期1月联考理科数学试题 Word版含答案
文档属性
| 名称 | 山西省运城市新绛县第二中学2021届高三上学期1月联考理科数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 1003.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 09:21:31 | ||
图片预览




文档简介
新绛县第二中学2021届高三上学期1月联考1177290012192000理科数学
考生注意:
1.本试卷分选择题和非选择题两部分.满分150分,考试时间120分钟.
2.答题前,考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚.
3.考生作答时,请将答案答在答题卡上.选择题每小题选出答案后,用false铅笔把答题卡上对应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区堿内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效.
4.本试卷主要命题范围:高考范围.
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知复数false(false为虚数单位),则false在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知全集false,集合false,则false( )
A.false B.false C.false D.false
3.“false”是“false”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
4.某校拟从1200名高一新生中采用系统抽样的方式抽取48人参加市“抗疫表彰大会”,如果编号为237的同学参加该表彰大会,那么下列编号中不能被抽到的是( )
A.1087 B.937 C.387 D.327
5.若单位向量false满足false,则false与false的夹角为( )
A.false B.false C.false D.false
6.摩索拉斯陵墓位于哈利卡纳素斯,在土耳其false的西南方,陵墓由下至上分别是墩座墙、柱子构成的拱廊、四棱锥金字塔以及由四匹马拉着的一架古代战车的雕像,总高度45米,其中墩座墙和柱子围成长、宽、高分别是40米、30米、32米的长方体,长方体的上底面与四棱锥的底面重合,顶点在底面的射影是长方形对角线交点,最顶部的马车雕像高6米,则陵墓的高与金字塔的侧棱长之比大约为(注:false)( )
A.2.77 B.2.43 C.1.73 D.1.35
7.若false,则( )
A.false B.false C.false D.false
8.函数false在区间false上的图象大致为( )
A. B. C. D.
9.在面积为false的false中,角false的对边分别为false,若false,则false( )
A.1 B.false C.2 D.3
10.已知函数false,则false( )
A.false B.false C.false D.false
11.点false为抛物线false的焦点,横坐标为false的点false为抛物线false上一点,过点false且与抛物线false相切的直线false与false轴相交于点false,则false( )
A.false B.false C.false D.false
12.已知函数false,若对任意false恒成立,则实数false的取值范围为( )
A.false B.false C.false D.false
二、填空题:本题共4小题,每小题5分,共20分.
13.已知实数false满足约束条件false则false的最小值为________.
14.已知false,则false_____.
15.已知双曲线false的右焦点为false为双曲线false的右顶点,过点false作false轴的垂线,与双曲线false交于false,若直线false的斜率是双曲线false的一条渐近线斜率的false倍,则双曲线false的离心率为_________.
16.在四棱锥false中,底面false是边长为2的正方形,侧面false底面false,且false,当false的面积最大时,四棱锥false的高为_______,四棱锥false外接球的表面积为________.(本小题第一空2分,第二空3分)
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(本小题满分12分)
已知数列false满足false,且false.
(1)求数列false的通项公式;
(2)令false,求数列false的前false项和false.
18.(本小题满分12分)
如图1中,多边形false为平面图形,其中false,将false沿false边折起,得到如图2所示四棱锥false,其中点false与点false重合.
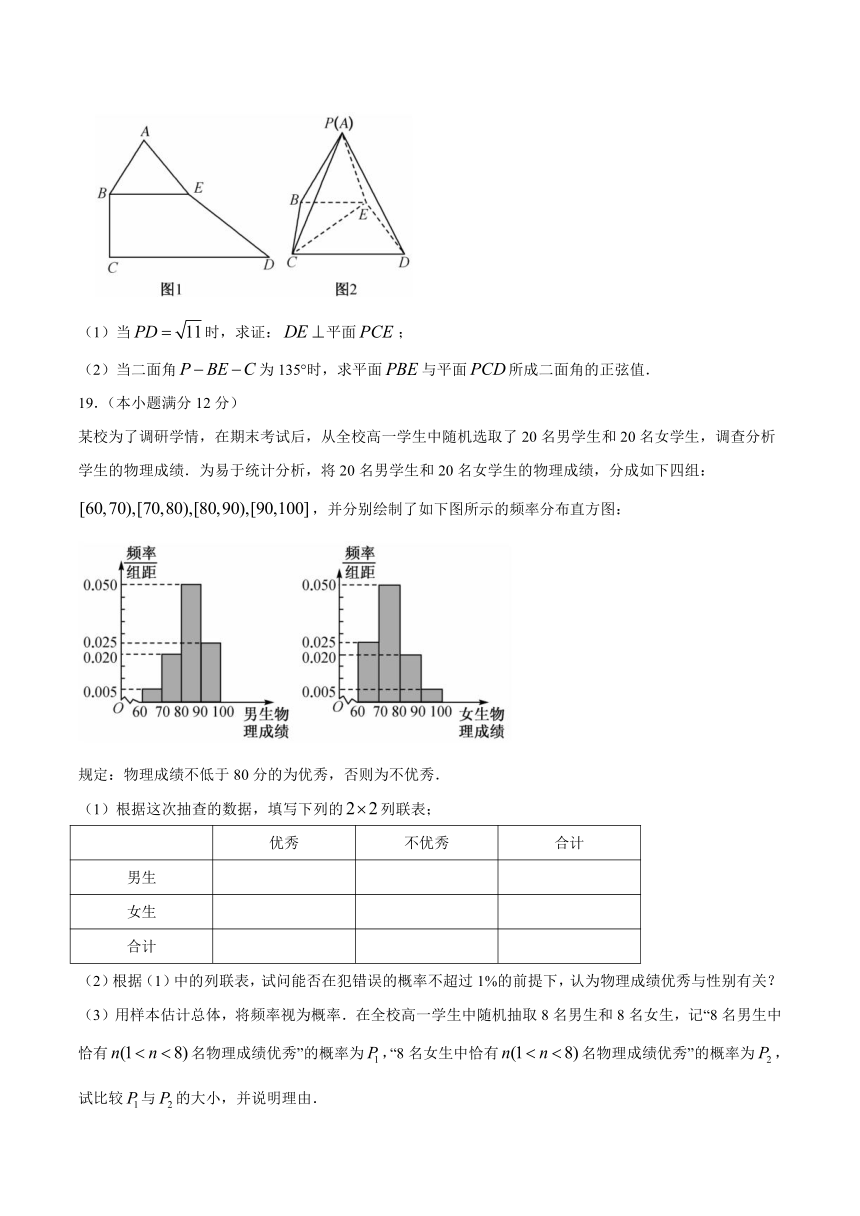
(1)当false时,求证:false平面false;
(2)当二面角false为135°时,求平面false与平面false所成二面角的正弦值.
19.(本小题满分12分)
某校为了调硏学情,在期末考试后,从全校高一学生中随机选取了20名男学生和20名女学生,调查分析学生的物理成绩.为易于统计分析,将20名男学生和20名女学生的物理成绩,分成如下四组:false,并分别绘制了如下图所示的频率分布直方图:
规定:物理成绩不低于80分的为优秀,否则为不优秀.
(1)根据这次抽查的数据,填写下列的false列联表;
优秀
不优秀
合计
男生
女生
合计
(2)根据(1)中的列联表,试问能否在犯错误的概率不超过1%的前提下,认为物理成绩优秀与性别有关?
(3)用样本估计总体,将频率视为概率.在全校高一学生中随机抽取8名男生和8名女生,记“8名男生中恰有false名物理成绩优秀”的概率为false,“8名女生中恰有false名物理成绩优秀”的概率为false,试比较false与false的大小,并说明理由.
附:临界值参考表与参考公式
false
0.15
0.10
0.05
0.025
0.010
0.005
0.001
false
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(false,其中false)
20.(本小题满分12分)
已知椭圆false的左、右焦点分别为false,过false且垂直于false轴的直线与false交于false两点,且false的坐标为false.
(1)求椭圆false的方程;
(2)过false作与直线false不重合的直线false与false相交于false两点,若直线false和直线false相交于点false,求证:点false在定直线上.
21.(本小题满分12分)
已知函数false.
(1)讨论函数false的单调性;
(2)若false,求证:false.
(二)选考题:共10分.请考生在第22、23两题中任选一题作答.如果多做,则按所做的第一题计分.
22.(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系false中,直线false的参数方程为false(false为参数),曲线false的参数方程为false(false为参数).以原点false为极点,false轴的正半轴为极轴,且两个坐标系取相等的长度单位,建立极坐标系.
(1)求直线false和曲线false的极坐标方程;
(2)已知false是曲线false上一点,false是直线false上位于极轴所在直线上方的一点,若false,求false面积的最大值.
23.(本小题满分10分)选修4-5:不等式选讲
设false,且false.
(1)求证:false;
(2)用false表示false的最大值,求false的最小值.
高三理科数学参考答案、提示及评分细则
1.A false,所以复数false在复平面内对应的点位于第一象限.故选A.
2.B 由false,得false,所以false.故选B.
3.A 由false,得false;由false,得false.故选A.
4.D 依据题意,抽样间隔为25,又237除以25的余数为12,故所抽取的编号为false,所以327不符合.故选D.
5.B 由false,得false,所以false,所以false,又false,所以false.故选B.
6.C 根据长、宽分别是40米、30米得金字塔的底面对角线长50米,可算出四棱锥高7米,所以侧棱长为false,则陵墓的高与金字塔的侧棱长之比大约为false.故选C.
7.C false,有false.故选C.
8.A 由false,可知false为偶函数,又由当false时,false.故选A.
9.B 由三角形的面积公式,得false,即false,由余弦定理,得false,所以false.故选B.
10.A 由题意有false,两式作差得false,有false,又false,所以false,又false,所以false,故false.故选A.
11.C 由抛物线的对称性,不妨设点false位于第一象限,可得点false的坐标为false,设直线false的方程为false,联立方程false消去false后整理为false,有false,有false,解得false,可得直线false的方程为false,令false,得false,直线false与false轴的交点false的坐标为false,所以false,又false,所以false,所以false,所以false.故选C.
12.D 由false,得false,令false,则问题可以转化为:对任意false恒成立,即函数false在false上单调递增,因为false,所以转化为false在false上恒成立,因为false,所以false在false上恒成立,即转化为false令false,则false,所以当false时,false,当false时,false,所以false在false上单调递增,在false上单调递减,所以false,所以false.故选D.
13.false 画出可行域(如图阴影部分),当直线false过点false时,false取得最小值,false的最小值为false.
14.false 对false两边分别求导,得false,令false,得false.
15.2 设焦点false的坐标为false,双曲线false的离心率为false,不妨设点false位于第一象限,可求得点false的坐标为false,点false的坐标为false,直线false的斜率为false,又由false,有false,整理为false,解得false或false(舍).
16.false false 点false在以弦false,所对的圆周角为60°的优弧false上运动,作false为垂足,由侧面false底面false,得false底面false.当false为false的中点时,false为等边三角形,此时false的面积最大,且false,即四棱锥false的高为false.设等边false的中心为false,正方形false的中心为false,过false、false分别作平面false、平面false的垂线,且交于点false,则false为四棱锥false外接球的球心,显然false,于是四棱锥false外接球的表面积为false.
17.解:(1)因为false,所以false,又false, 3分
所以数列false是首项为1,公差为1的等差数列. 4分
所以false,得false,
即数列false的通项公式为false. 6分
(2)由(1),得falsefalse, 9分
则falsefalse. 12分
18.(1)证明:由false,易求false,所以false,所以false. 2分
因为false,所以false,所以false.
又false平面false,
所以false平面false. 5分
(2)解:取false的中点false,过点false在平面false内作false的垂线交false于false,以直线false作为false轴,直线false为false轴,过点false作平面false的垂线为false轴,建立空间直角坐标系,则false. 6分
因为false为false的中点,所以false,又false,所以false.
在false中,false,所以false,所以false,
所以false. 8分
设平面false的法向量为false,
由false,有false解得false令false,得false; 9分
设平面false的法向量为false,
由false,有false解得false令false,
得false, 10分
所以false,
故平面false与平面false所成二面角的正弦值为false. 12分
19.解:(1)列出false列联表,如下:
优秀
不优秀
合计
男生
15
5
20
女生
5
15
20
合计
20
20
40
3分
(2)false,
所以能在犯错误的概率不超过1%的前提下,认为物理成绩优秀与性别有关. 6分
(3)根据频率分布直方图,可得男生物理成绩优秀的概率为false,
女生物理成绩优秀的概率为false. 7分
设“8名男生中物理成绩优秀”的人数为随机变量false,“8名女生中物理成绩优秀”的人数为随机变量false,根据题意,得false, 8分
则falsefalse, 10分
当false时,false,于是false;
当false时,false,于是false;
当false时,false,于是false. 12分
20.(1)解:由题意,得false,且false, 1分
则false,即false, 2分
所以false, 3分
故椭圆false的方程为false. 4分
(2)证明:由(1)及false的对称性,得点false的坐标为false, 5分
设直线false的方程为false,点false的坐标分别为false,
联立方程false消去false后整理为false,
所以false. 6分
直线false的斜率为false,
直线false的方程为false,
直线false的斜率为false,
直线false的方程为false, 8分
将直线false和直线false方程作差消去false后整理为false,
可得false, 9分
而由false,
可得false,解得false,即直线false和false的交点false的横坐标恒为4, 11分
所以点false在定直线false上. 12分
21.(1)解:false的定义域为false. 1分
令false,方程false的判别式false,
(i)当false,即false时,false恒成立,即对任意false,所以false在false上单调递增. 2分
(ii)当false,即false或false.
①当false时,false恒成立,即对任意false,所以false在false上单调递增. 3分
②当false时,由false,解得false.所以当false时,false;当false时,false;当false时,false,所以在false上,false,在false上,false,所以函数false在false和false上单调递增;在false上单调递减. 6分
综上,当false时,false在false上单调递增;当false时,false在false和false上单调递增,在false上单调递减. 7分
(2)证明:由false,得false,所以false, 8分
因为false,所以false,令false,则false,
所以false,
所以false. 10分
所以要证false,只要证false,即证false. 11分
由(1)可知,当false时,所以false在false上是增函数,
所以,当false时,false,即false成立,
所以false成立. 12分
22.解:(1)由false的参数方程得false的普通方程为false,所以false的倾斜角为false,所以直线false的极坐标方程为false; 2分
由曲线false的参数方程得false的普通方程为false,又false所以曲线false的极坐标方程为false. 4分
(2)由false,则false的极坐标为false.
设false,
则false
false
false. 8分
当false,即false时,false. 10分
23.(1)证明:因为false(当且仅当false时等号成立),false(当且仅当false时等号成立),false(当且仅当false时等号成立),
所以falsefalse,
由false,得false(当且仅当false时等号成立). 5分
(2)解:设false,则false,
从而false,即false. 8分
当且仅当false,即false时,
false. 10分
考生注意:
1.本试卷分选择题和非选择题两部分.满分150分,考试时间120分钟.
2.答题前,考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚.
3.考生作答时,请将答案答在答题卡上.选择题每小题选出答案后,用false铅笔把答题卡上对应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区堿内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效.
4.本试卷主要命题范围:高考范围.
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知复数false(false为虚数单位),则false在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知全集false,集合false,则false( )
A.false B.false C.false D.false
3.“false”是“false”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
4.某校拟从1200名高一新生中采用系统抽样的方式抽取48人参加市“抗疫表彰大会”,如果编号为237的同学参加该表彰大会,那么下列编号中不能被抽到的是( )
A.1087 B.937 C.387 D.327
5.若单位向量false满足false,则false与false的夹角为( )
A.false B.false C.false D.false
6.摩索拉斯陵墓位于哈利卡纳素斯,在土耳其false的西南方,陵墓由下至上分别是墩座墙、柱子构成的拱廊、四棱锥金字塔以及由四匹马拉着的一架古代战车的雕像,总高度45米,其中墩座墙和柱子围成长、宽、高分别是40米、30米、32米的长方体,长方体的上底面与四棱锥的底面重合,顶点在底面的射影是长方形对角线交点,最顶部的马车雕像高6米,则陵墓的高与金字塔的侧棱长之比大约为(注:false)( )
A.2.77 B.2.43 C.1.73 D.1.35
7.若false,则( )
A.false B.false C.false D.false
8.函数false在区间false上的图象大致为( )
A. B. C. D.
9.在面积为false的false中,角false的对边分别为false,若false,则false( )
A.1 B.false C.2 D.3
10.已知函数false,则false( )
A.false B.false C.false D.false
11.点false为抛物线false的焦点,横坐标为false的点false为抛物线false上一点,过点false且与抛物线false相切的直线false与false轴相交于点false,则false( )
A.false B.false C.false D.false
12.已知函数false,若对任意false恒成立,则实数false的取值范围为( )
A.false B.false C.false D.false
二、填空题:本题共4小题,每小题5分,共20分.
13.已知实数false满足约束条件false则false的最小值为________.
14.已知false,则false_____.
15.已知双曲线false的右焦点为false为双曲线false的右顶点,过点false作false轴的垂线,与双曲线false交于false,若直线false的斜率是双曲线false的一条渐近线斜率的false倍,则双曲线false的离心率为_________.
16.在四棱锥false中,底面false是边长为2的正方形,侧面false底面false,且false,当false的面积最大时,四棱锥false的高为_______,四棱锥false外接球的表面积为________.(本小题第一空2分,第二空3分)
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(本小题满分12分)
已知数列false满足false,且false.
(1)求数列false的通项公式;
(2)令false,求数列false的前false项和false.
18.(本小题满分12分)
如图1中,多边形false为平面图形,其中false,将false沿false边折起,得到如图2所示四棱锥false,其中点false与点false重合.
(1)当false时,求证:false平面false;
(2)当二面角false为135°时,求平面false与平面false所成二面角的正弦值.
19.(本小题满分12分)
某校为了调硏学情,在期末考试后,从全校高一学生中随机选取了20名男学生和20名女学生,调查分析学生的物理成绩.为易于统计分析,将20名男学生和20名女学生的物理成绩,分成如下四组:false,并分别绘制了如下图所示的频率分布直方图:
规定:物理成绩不低于80分的为优秀,否则为不优秀.
(1)根据这次抽查的数据,填写下列的false列联表;
优秀
不优秀
合计
男生
女生
合计
(2)根据(1)中的列联表,试问能否在犯错误的概率不超过1%的前提下,认为物理成绩优秀与性别有关?
(3)用样本估计总体,将频率视为概率.在全校高一学生中随机抽取8名男生和8名女生,记“8名男生中恰有false名物理成绩优秀”的概率为false,“8名女生中恰有false名物理成绩优秀”的概率为false,试比较false与false的大小,并说明理由.
附:临界值参考表与参考公式
false
0.15
0.10
0.05
0.025
0.010
0.005
0.001
false
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(false,其中false)
20.(本小题满分12分)
已知椭圆false的左、右焦点分别为false,过false且垂直于false轴的直线与false交于false两点,且false的坐标为false.
(1)求椭圆false的方程;
(2)过false作与直线false不重合的直线false与false相交于false两点,若直线false和直线false相交于点false,求证:点false在定直线上.
21.(本小题满分12分)
已知函数false.
(1)讨论函数false的单调性;
(2)若false,求证:false.
(二)选考题:共10分.请考生在第22、23两题中任选一题作答.如果多做,则按所做的第一题计分.
22.(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系false中,直线false的参数方程为false(false为参数),曲线false的参数方程为false(false为参数).以原点false为极点,false轴的正半轴为极轴,且两个坐标系取相等的长度单位,建立极坐标系.
(1)求直线false和曲线false的极坐标方程;
(2)已知false是曲线false上一点,false是直线false上位于极轴所在直线上方的一点,若false,求false面积的最大值.
23.(本小题满分10分)选修4-5:不等式选讲
设false,且false.
(1)求证:false;
(2)用false表示false的最大值,求false的最小值.
高三理科数学参考答案、提示及评分细则
1.A false,所以复数false在复平面内对应的点位于第一象限.故选A.
2.B 由false,得false,所以false.故选B.
3.A 由false,得false;由false,得false.故选A.
4.D 依据题意,抽样间隔为25,又237除以25的余数为12,故所抽取的编号为false,所以327不符合.故选D.
5.B 由false,得false,所以false,所以false,又false,所以false.故选B.
6.C 根据长、宽分别是40米、30米得金字塔的底面对角线长50米,可算出四棱锥高7米,所以侧棱长为false,则陵墓的高与金字塔的侧棱长之比大约为false.故选C.
7.C false,有false.故选C.
8.A 由false,可知false为偶函数,又由当false时,false.故选A.
9.B 由三角形的面积公式,得false,即false,由余弦定理,得false,所以false.故选B.
10.A 由题意有false,两式作差得false,有false,又false,所以false,又false,所以false,故false.故选A.
11.C 由抛物线的对称性,不妨设点false位于第一象限,可得点false的坐标为false,设直线false的方程为false,联立方程false消去false后整理为false,有false,有false,解得false,可得直线false的方程为false,令false,得false,直线false与false轴的交点false的坐标为false,所以false,又false,所以false,所以false,所以false.故选C.
12.D 由false,得false,令false,则问题可以转化为:对任意false恒成立,即函数false在false上单调递增,因为false,所以转化为false在false上恒成立,因为false,所以false在false上恒成立,即转化为false令false,则false,所以当false时,false,当false时,false,所以false在false上单调递增,在false上单调递减,所以false,所以false.故选D.
13.false 画出可行域(如图阴影部分),当直线false过点false时,false取得最小值,false的最小值为false.
14.false 对false两边分别求导,得false,令false,得false.
15.2 设焦点false的坐标为false,双曲线false的离心率为false,不妨设点false位于第一象限,可求得点false的坐标为false,点false的坐标为false,直线false的斜率为false,又由false,有false,整理为false,解得false或false(舍).
16.false false 点false在以弦false,所对的圆周角为60°的优弧false上运动,作false为垂足,由侧面false底面false,得false底面false.当false为false的中点时,false为等边三角形,此时false的面积最大,且false,即四棱锥false的高为false.设等边false的中心为false,正方形false的中心为false,过false、false分别作平面false、平面false的垂线,且交于点false,则false为四棱锥false外接球的球心,显然false,于是四棱锥false外接球的表面积为false.
17.解:(1)因为false,所以false,又false, 3分
所以数列false是首项为1,公差为1的等差数列. 4分
所以false,得false,
即数列false的通项公式为false. 6分
(2)由(1),得falsefalse, 9分
则falsefalse. 12分
18.(1)证明:由false,易求false,所以false,所以false. 2分
因为false,所以false,所以false.
又false平面false,
所以false平面false. 5分
(2)解:取false的中点false,过点false在平面false内作false的垂线交false于false,以直线false作为false轴,直线false为false轴,过点false作平面false的垂线为false轴,建立空间直角坐标系,则false. 6分
因为false为false的中点,所以false,又false,所以false.
在false中,false,所以false,所以false,
所以false. 8分
设平面false的法向量为false,
由false,有false解得false令false,得false; 9分
设平面false的法向量为false,
由false,有false解得false令false,
得false, 10分
所以false,
故平面false与平面false所成二面角的正弦值为false. 12分
19.解:(1)列出false列联表,如下:
优秀
不优秀
合计
男生
15
5
20
女生
5
15
20
合计
20
20
40
3分
(2)false,
所以能在犯错误的概率不超过1%的前提下,认为物理成绩优秀与性别有关. 6分
(3)根据频率分布直方图,可得男生物理成绩优秀的概率为false,
女生物理成绩优秀的概率为false. 7分
设“8名男生中物理成绩优秀”的人数为随机变量false,“8名女生中物理成绩优秀”的人数为随机变量false,根据题意,得false, 8分
则falsefalse, 10分
当false时,false,于是false;
当false时,false,于是false;
当false时,false,于是false. 12分
20.(1)解:由题意,得false,且false, 1分
则false,即false, 2分
所以false, 3分
故椭圆false的方程为false. 4分
(2)证明:由(1)及false的对称性,得点false的坐标为false, 5分
设直线false的方程为false,点false的坐标分别为false,
联立方程false消去false后整理为false,
所以false. 6分
直线false的斜率为false,
直线false的方程为false,
直线false的斜率为false,
直线false的方程为false, 8分
将直线false和直线false方程作差消去false后整理为false,
可得false, 9分
而由false,
可得false,解得false,即直线false和false的交点false的横坐标恒为4, 11分
所以点false在定直线false上. 12分
21.(1)解:false的定义域为false. 1分
令false,方程false的判别式false,
(i)当false,即false时,false恒成立,即对任意false,所以false在false上单调递增. 2分
(ii)当false,即false或false.
①当false时,false恒成立,即对任意false,所以false在false上单调递增. 3分
②当false时,由false,解得false.所以当false时,false;当false时,false;当false时,false,所以在false上,false,在false上,false,所以函数false在false和false上单调递增;在false上单调递减. 6分
综上,当false时,false在false上单调递增;当false时,false在false和false上单调递增,在false上单调递减. 7分
(2)证明:由false,得false,所以false, 8分
因为false,所以false,令false,则false,
所以false,
所以false. 10分
所以要证false,只要证false,即证false. 11分
由(1)可知,当false时,所以false在false上是增函数,
所以,当false时,false,即false成立,
所以false成立. 12分
22.解:(1)由false的参数方程得false的普通方程为false,所以false的倾斜角为false,所以直线false的极坐标方程为false; 2分
由曲线false的参数方程得false的普通方程为false,又false所以曲线false的极坐标方程为false. 4分
(2)由false,则false的极坐标为false.
设false,
则false
false
false. 8分
当false,即false时,false. 10分
23.(1)证明:因为false(当且仅当false时等号成立),false(当且仅当false时等号成立),false(当且仅当false时等号成立),
所以falsefalse,
由false,得false(当且仅当false时等号成立). 5分
(2)解:设false,则false,
从而false,即false. 8分
当且仅当false,即false时,
false. 10分
同课章节目录
