【课时作业】3.7 切线长定理(含答案)
文档属性
| 名称 | 【课时作业】3.7 切线长定理(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 312.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 17:08:49 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2020-2021学年九年级数学下册课时作业(北师版)
第三章 圆
*7 切线长定理
一、选择题
1.下列说法正确的是( )
A.切线长就是圆的切线的长度
B.过平面上任一点,都可作圆的切线
C.过圆外一点,只能作一条圆的切线
D.切线是直线,切线长是线段的长度
2.PA,PB切⊙O于A,B两点,若点C为优弧AB上一点,∠P=50°,则∠ACB等于( )
A.50° B.130° C.65° D.70°
3.如图,PA,PB为⊙O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交⊙O于点D,下列结论不一定成立的是( )
A.PA=PB B.∠BPD=∠APD
C.AB⊥PD D.AB平分PD
4.从⊙O外一点P作⊙O的两条切线PA,PB,切点为A,B,若AB=16,AB的弦心距为6,则PA的长为( )
A. B. C.10 D.16
5.如图,四边形ABCD四边分别切⊙O于点E,F,G,H,下列结论一定正确的有( )
①AF=BG;②CG=CH;③AB+CD=AB+BC;④BGA.1个 B.2个 C.3个 D.4个
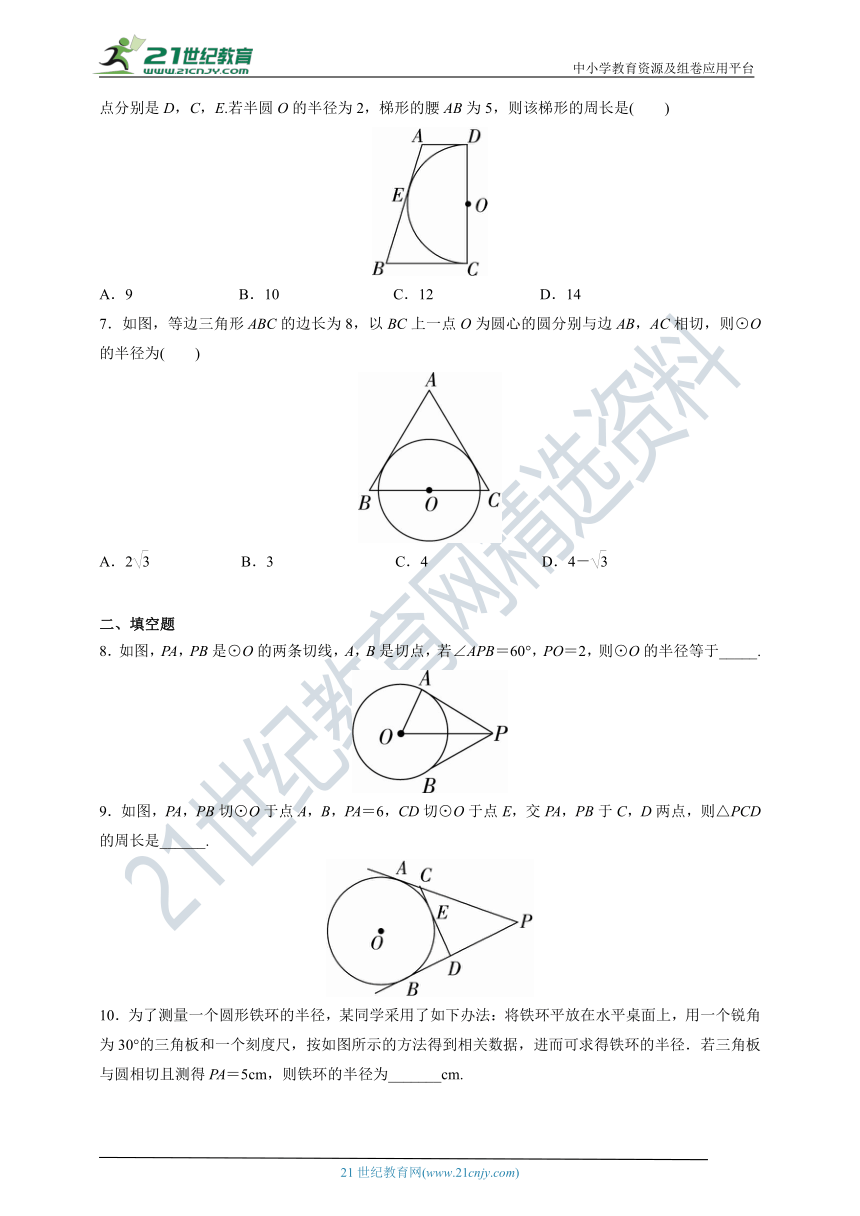
6.已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是( )
A.9 B.10 C.12 D.14
7.如图,等边三角形ABC的边长为8,以BC上一点O为圆心的圆分别与边AB,AC相切,则⊙O的半径为( )
A.2 B.3 C.4 D.4-
二、填空题
8.如图,PA,PB是⊙O的两条切线,A,B是切点,若∠APB=60°,PO=2,则⊙O的半径等于_____.
9.如图,PA,PB切⊙O于点A,B,PA=6,CD切⊙O于点E,交PA,PB于C,D两点,则△PCD的周长是______.
10.为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径.若三角板与圆相切且测得PA=5cm,则铁环的半径为_______cm.
11.如图,在Rt△ABC中,∠ACB=90°,AC=3cm,BC=6cm,以斜边AB上的一点O为圆心所作的半圆分别与AC,BC相切于点D,E,则⊙O的半径为_____cm.
三、解答题
12.如图①,一个圆球放置在V形架中,图②是它的平面示意图,CA和CB都是⊙O的切线,切点分别是A,B.如果⊙O的半径为2cm,且AB=6cm,求∠ACB.
图① 图②
13.如图,直线AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,OB=3cm,OC=4cm.求(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
14.如图,PA,PB分别切⊙O于点A,B,E为劣弧AB上一点,过E点的切线交PA于点C,交PB于点D.
(1)若PA=8,求△PCD的周长.
(2)若∠P=50°,求∠DOC.
15.如图,AB,BC,CD分别与⊙O切于点E,F,G,且AB∥CD.连接OB,OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于点N.
(1)求证:MN是⊙O的切线;
(2)当OB=6cm,OC=8cm时,求⊙O的半径及MN的长.
参 考 答 案
1. D 2. C 3. D 4. B 5. B 6. D 7. A
8. 1
9. 12
10. 5
11. 2
12. 解:连接OC交AB于点D.∵CA,CB分别是⊙O的切线,∴CA=CB,OC平分∠ACB,∴OC⊥AB.∵AB=6,∴BD=3.在Rt△OBD中,∵OB=2,sin∠BOD==,∴∠BOD=60°.∵B是切点,∴OB⊥BC,∴∠OCB=30°,∴∠ACB=60°.
13. 解:(1)连接OF,根据切线长定理得,BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG.∵AB∥CD,∴∠ABC+∠BCD=180°,∴∠OBF+∠OCF=90°,∴∠BOC=90°.
(2)由(1)知,∠BOC=90°.∵OB=3cm,OC=4cm,∴由勾股定理得到:BC==5cm,∴BE+CG=BF+CF=BC=5cm. (3)∵OF⊥BC,∴OB·OC=BC·OF,∴OF==2.4cm.
14. 解:(1)连接OE,∵PA,PB与⊙O相切,∴PA=PB=8,同理,AC=CE,BD=DE,∴△PCD的周长=PC+PD+CD=PC+PD+CE+DE=PA+PB=16.
(2)∵PA,PB与⊙O相切,∴∠OAP=∠OBP=90°.又∠P=50°,∵∠AOB=360°-90°-90°-50°=130°.在Rt△AOC和Rt△EOC中, ∴Rt△AOC≌Rt△EOC(HL),∴∠AOC=∠COE.同理,∠DOE=∠BOD,∴∠COD=∠AOB=65°.
15. (1)证明:∵AB,BC,CD分别与⊙O切于点E,F,G,∴∠OBC=∠ABC,∠OCB=∠DCB.∵AB∥CD,∴∠ABC+∠DCB=180°.∴∠OBC+∠OCB=(∠ABC+∠DCB)=×180°=90°,∴∠BOC=180°-(∠OBC+∠OCB)=180°-90°=90°.∵MN∥OB,∴∠NMC=∠BOC=90°.∴MN是⊙O的切线.
(2)解:连接OF,则OF⊥BC.由(1)知,△BOC是直角三角形,∴BC===10(cm).∵S△BOC=OB·OC=BC·OF,∴6×8=10×OF.∴OF=4.8(cm).即⊙O的半径为4.8cm.由(1)知,∠NCM=∠BCO,∠NMC=∠BOC=90°,∴△NMC∽△BOC.∴=.即=.∴MN=9.6cm.
_21?????????è?????(www.21cnjy.com)_
2020-2021学年九年级数学下册课时作业(北师版)
第三章 圆
*7 切线长定理
一、选择题
1.下列说法正确的是( )
A.切线长就是圆的切线的长度
B.过平面上任一点,都可作圆的切线
C.过圆外一点,只能作一条圆的切线
D.切线是直线,切线长是线段的长度
2.PA,PB切⊙O于A,B两点,若点C为优弧AB上一点,∠P=50°,则∠ACB等于( )
A.50° B.130° C.65° D.70°
3.如图,PA,PB为⊙O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交⊙O于点D,下列结论不一定成立的是( )
A.PA=PB B.∠BPD=∠APD
C.AB⊥PD D.AB平分PD
4.从⊙O外一点P作⊙O的两条切线PA,PB,切点为A,B,若AB=16,AB的弦心距为6,则PA的长为( )
A. B. C.10 D.16
5.如图,四边形ABCD四边分别切⊙O于点E,F,G,H,下列结论一定正确的有( )
①AF=BG;②CG=CH;③AB+CD=AB+BC;④BG
6.已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是( )
A.9 B.10 C.12 D.14
7.如图,等边三角形ABC的边长为8,以BC上一点O为圆心的圆分别与边AB,AC相切,则⊙O的半径为( )
A.2 B.3 C.4 D.4-
二、填空题
8.如图,PA,PB是⊙O的两条切线,A,B是切点,若∠APB=60°,PO=2,则⊙O的半径等于_____.
9.如图,PA,PB切⊙O于点A,B,PA=6,CD切⊙O于点E,交PA,PB于C,D两点,则△PCD的周长是______.
10.为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径.若三角板与圆相切且测得PA=5cm,则铁环的半径为_______cm.
11.如图,在Rt△ABC中,∠ACB=90°,AC=3cm,BC=6cm,以斜边AB上的一点O为圆心所作的半圆分别与AC,BC相切于点D,E,则⊙O的半径为_____cm.
三、解答题
12.如图①,一个圆球放置在V形架中,图②是它的平面示意图,CA和CB都是⊙O的切线,切点分别是A,B.如果⊙O的半径为2cm,且AB=6cm,求∠ACB.
图① 图②
13.如图,直线AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,OB=3cm,OC=4cm.求(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
14.如图,PA,PB分别切⊙O于点A,B,E为劣弧AB上一点,过E点的切线交PA于点C,交PB于点D.
(1)若PA=8,求△PCD的周长.
(2)若∠P=50°,求∠DOC.
15.如图,AB,BC,CD分别与⊙O切于点E,F,G,且AB∥CD.连接OB,OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于点N.
(1)求证:MN是⊙O的切线;
(2)当OB=6cm,OC=8cm时,求⊙O的半径及MN的长.
参 考 答 案
1. D 2. C 3. D 4. B 5. B 6. D 7. A
8. 1
9. 12
10. 5
11. 2
12. 解:连接OC交AB于点D.∵CA,CB分别是⊙O的切线,∴CA=CB,OC平分∠ACB,∴OC⊥AB.∵AB=6,∴BD=3.在Rt△OBD中,∵OB=2,sin∠BOD==,∴∠BOD=60°.∵B是切点,∴OB⊥BC,∴∠OCB=30°,∴∠ACB=60°.
13. 解:(1)连接OF,根据切线长定理得,BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG.∵AB∥CD,∴∠ABC+∠BCD=180°,∴∠OBF+∠OCF=90°,∴∠BOC=90°.
(2)由(1)知,∠BOC=90°.∵OB=3cm,OC=4cm,∴由勾股定理得到:BC==5cm,∴BE+CG=BF+CF=BC=5cm. (3)∵OF⊥BC,∴OB·OC=BC·OF,∴OF==2.4cm.
14. 解:(1)连接OE,∵PA,PB与⊙O相切,∴PA=PB=8,同理,AC=CE,BD=DE,∴△PCD的周长=PC+PD+CD=PC+PD+CE+DE=PA+PB=16.
(2)∵PA,PB与⊙O相切,∴∠OAP=∠OBP=90°.又∠P=50°,∵∠AOB=360°-90°-90°-50°=130°.在Rt△AOC和Rt△EOC中, ∴Rt△AOC≌Rt△EOC(HL),∴∠AOC=∠COE.同理,∠DOE=∠BOD,∴∠COD=∠AOB=65°.
15. (1)证明:∵AB,BC,CD分别与⊙O切于点E,F,G,∴∠OBC=∠ABC,∠OCB=∠DCB.∵AB∥CD,∴∠ABC+∠DCB=180°.∴∠OBC+∠OCB=(∠ABC+∠DCB)=×180°=90°,∴∠BOC=180°-(∠OBC+∠OCB)=180°-90°=90°.∵MN∥OB,∴∠NMC=∠BOC=90°.∴MN是⊙O的切线.
(2)解:连接OF,则OF⊥BC.由(1)知,△BOC是直角三角形,∴BC===10(cm).∵S△BOC=OB·OC=BC·OF,∴6×8=10×OF.∴OF=4.8(cm).即⊙O的半径为4.8cm.由(1)知,∠NCM=∠BCO,∠NMC=∠BOC=90°,∴△NMC∽△BOC.∴=.即=.∴MN=9.6cm.
_21?????????è?????(www.21cnjy.com)_
