2020——2021学年苏科版七年级数学下册7.4认识三角形考点同步训练(Word版 含解析)
文档属性
| 名称 | 2020——2021学年苏科版七年级数学下册7.4认识三角形考点同步训练(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 327.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 00:00:00 | ||
图片预览




文档简介
2021年苏科新版七年级数学下册7.4认识三角形分考点同步训练(附答案)
考点一.三角形:
1.如图,图中直角三角形共有( )
A.1个 B.2个 C.3个 D.4个
2.某同学在纸上画了四个点,如果把这四个点彼此连接,连成一个图形,则这个图形中会有 个三角形出现.
3.如图,直角三角形的个数为 .
4.过A、B、C、D、E五个点中任意三点画三角形;
(1)其中以AB为一边可以画出 个三角形;
(2)其中以C为顶点可以画出 个三角形.
考点二.三角形的角平分线、中线和高:
5.用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )
A.B. C.D.
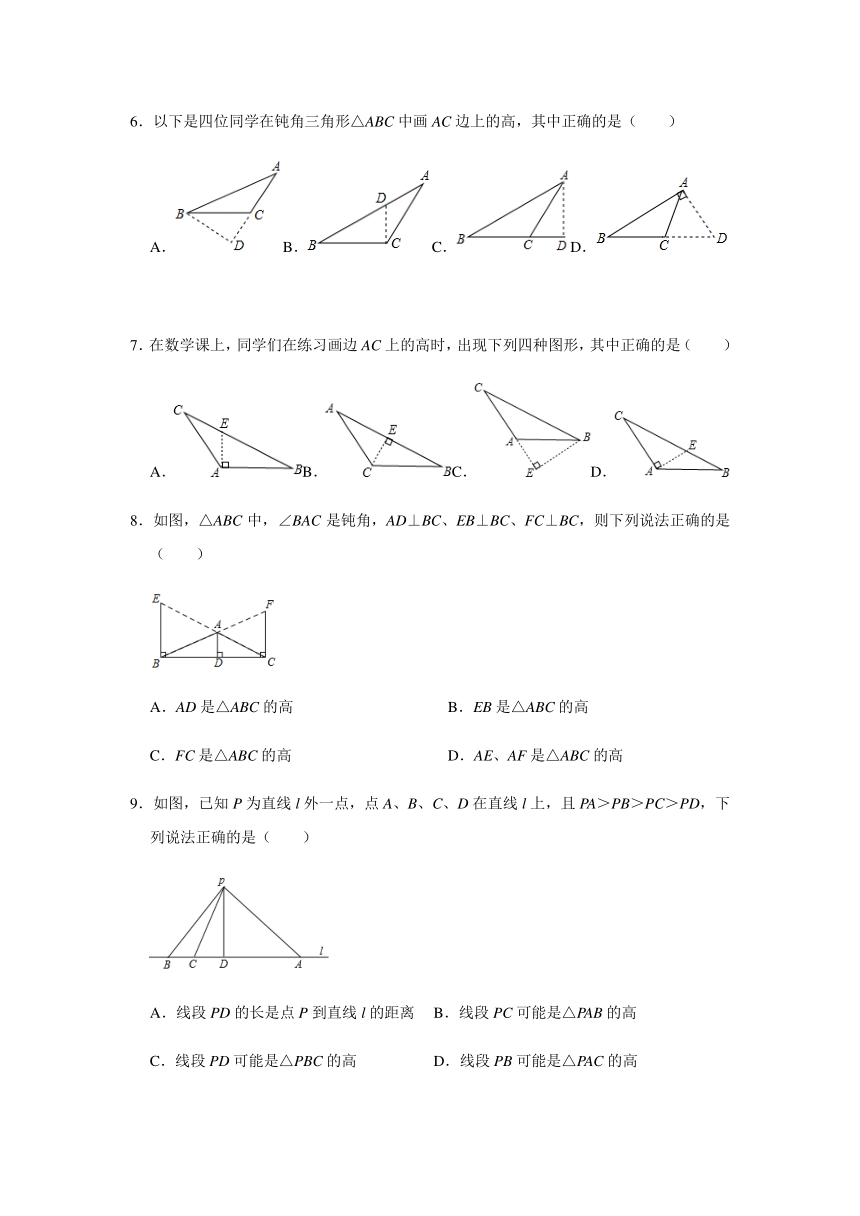
6.以下是四位同学在钝角三角形△ABC中画AC边上的高,其中正确的是( )
A.B.C.D.
7.在数学课上,同学们在练习画边AC上的高时,出现下列四种图形,其中正确的是( )
A.B.C.D.
8.如图,△ABC中,∠BAC是钝角,AD⊥BC、EB⊥BC、FC⊥BC,则下列说法正确的是( )
A.AD是△ABC的高 B.EB是△ABC的高
C.FC是△ABC的高 D.AE、AF是△ABC的高
9.如图,已知P为直线l外一点,点A、B、C、D在直线l上,且PA>PB>PC>PD,下列说法正确的是( )
A.线段PD的长是点P到直线l的距离 B.线段PC可能是△PAB的高
C.线段PD可能是△PBC的高 D.线段PB可能是△PAC的高
10.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等边三角形
11.如图,在四边形ABCD中,AB∥CD,3AB=4AD=6CD,E为AB的中点.萧钟同学用无刻度的直尺先连接CE交BD于点F,再连接AF.则线段AF是△ABD的( )
A.中线 B.高线 C.角平分线 D.中线、高线、角平分线(三线合一)
12.如图,D、E分别是△ABC的边AC、BC的中点,则下列说法不正确的是( )
A.DE是△ABC的中线 B.BD是△ABC的中线
C.AD=DC,BE=EC D.DE是△BCD的中线
13.如图,AD⊥BC于D,BE⊥AC于E,CF⊥AB于F,GA⊥AC于A,在△ABC中,AB边上的高为( )
A.AD B.GA C.BE D.CF
14.如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,AD与BE交于H,则∠CHD= .
15.在△ABC中,AC=5cm,AD是△ABC中线,若△ABD周长与△ADC的周长相差2cm,则BA= cm.
16.如图,在△ABC中(AB>BC),AB=2AC,AC边上中线BD把△ABC的周长分成30和20两部分,求AB和BC的长.
17.如图,△ABC的周长是21cm,AB=AC,中线BD分△ABC为两个三角形,且△ABD的周长比△BCD的周长大6cm,求AB,BC.
18.已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则
①∠ABO的度数是 ;
②当∠BAD=∠ABD时,x= ;当∠BAD=∠BDA时,x= .
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
考点三.三角形的面积:
19.如图,AD是△ABC的中线,DE是△ADC的高线,AB=3,AC=5,DE=2,那么点D到AB的距离是( )
A. B. C. D.2
20.如图,在△ABC中,已知点E、F分别是AD、CE边上的中点,且S△BEF=4cm2,则S△ABC的值为( )
A.1cm2 B.2cm2 C.8cm2 D.16cm2
21.已知AD是△ABC的中线,BE是△ABD的中线,若△ABC的面积为18,则△ABE的面积为( )
A.5 B.4.5
C.4 D.9
22.如图,D,E,F分别是边BC,AD,AC上的中点,若S四边形的面积为3,则△ABC的面积是( )
A.5 B.6 C.7 D.8
23.如图,长方形ABCD中,AB=4cm,BC=3cm,点E是CD的中点,动点P从A点出发,以每秒1cm的速度沿A→B→C→E运动,最终到达点E.若点P运动的时间为x秒,那么当x= 时,△APE的面积等于5.
24.把一张三角形的纸折叠成如图后,面积减少,已知阴影部分的面积是50平方厘米,则这张三角形纸的面积是 平方分米.
考点四.三角形的稳定性:
25.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
A.两点之间的线段最短 B.三角形具有稳定性
C.长方形是轴对称图形 D.长方形的四个角都是直角
26.下列图形中不具有稳定性是( )
A.B.C.D.
27.用八根木条钉成如图所示的八边形木架,要使它不变形,至少要钉上木条的根数是( )
A.3根 B.4根 C.5根 D.6根
考点五.三角形的重心:
28.三角形的重心是( )
A.三角形三条边上中线的交点 B.三角形三条边上高线的交点
C.三角形三条边垂直平分线的交点 D.三角形三条内角平分线的交点
29.在Rt△ABC中,AD是斜边BC边上的中线,G是△ABC重心,如果BC=6,那么线段AG的长为 .
考点六.三角形三边关系:
30.下列长度的三条线段能组成三角形的是( )
A.3,4,8 B.5,6,11 C.5,6,10 D.1,2,3
31.如图,为估计池塘岸边A、B两点的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是( )
A.5米 B.10米 C.15米 D.20米
32.已知关于x的不等式组至少有两个整数解,且存在以3,a,7为边的三角形,则a的整数解有( )
A.4个 B.5个 C.6个 D.7个
33.若a、b、c为△ABC的三边长,且满足|a﹣4|+=0,则c的值可以为( )
A.5 B.6 C.7 D.8
34.已知三角形两边的长分别是4和10,则此三角形第三边的长可能是( )
A.5 B.6 C.12 D.16
35.△ABC中,AB=10,BC=2x,AC=3x,则x的取值范围 .
36.在△ABC中,若AB=4,BC=2,且AC的长为偶数,则AC= .
37.若a、b、c为三角形的三边,且a、b满足+(b﹣2)2=0,第三边c为奇数,则c= .
38.三角形的两边长分别是3和4,第三边长是方程x2﹣13x+40=0的根,则该三角形的周长为 .
39.如图:已知AD为△ABC的中线,且∠1=∠2,∠3=∠4,求证:BE+CF>EF.
40.在△ABC中,AB=5,AC=3,AD是BC边上的中线,则AD的取值范围是 .
参考答案
1.解:如图,图中直角三角形有Rt△ABD、Rt△BDC、Rt△ABC,共有3个,
故选:C.
2.解:∵①当四个点共线时,不能作出三角形;
②当三个点共线,第四个点不在这条直线上时,能够画出3个三角形;
③若4个点能构成凹四边形,则能画出4个三角形;
④当任意的三个点不共线时,则能够画出8个三角形.
∴0或3或4或8.
3.解:如图,直角三角形有:△ADC、△BCD、△CDE、△BDE、△ACE、△ACB,一共6个,
故答案为:6.
4.解:(1)如图,以AB为一边的三角形有△ABC、△ABD、△ABE共3个;
(2)如图,以点C为顶点的三角形有△ABC、△BEC、△BCD、△ACE、△ACD、△CDE共6个.
故答案为:(1)3,(2)6.
5.解:B,C,D都不是△ABC的边BC上的高,
故选:A.
6.解:A、高BD交AC的延长线于点D处,符合题意;
B、没有经过顶点B,不符合题意;
C、做的是BC边上的高线AD,不符合题意;
D、没有经过顶点B,不符合题意.
故选:A.
7.解:AC边上的高应该是过B作垂线段AC,符合这个条件的是C;
A,B,D都不过B点,故错误;
故选:C.
8.解:△ABC中,画BC边上的高,是线段AD.
故选:A.
9.解:A.线段PD的长不一定是点P到直线l的距离,故本选项错误;
B.线段PC不可能是△PAB的高,故本选项错误;
C.线段PD可能是△PBC的高,故本选项正确;
D.线段PB不可能是△PAC的高,故本选项错误;
故选:C.
10.解:一个三角形的三条高的交点恰是三角形的一个顶点,这个三角形是直角三角形.
故选:C.
11.解:∵3AB=6CD,E为AB的中点,
∴CD=AB,BE=AB,
∴CD=BE,
又∵AB∥CD,
∴∠EBF=∠CDF,
又∵∠EFB=∠CFD,
∴△BEF≌△DCF(AAS),
∴BF=DF,
∴线段AF是△ABD的中线,
故选:A.
12.解:∵D、E分别是△ABC的边AC、BC的中点,
∴DE是△ABC的中位线,不是中线;BD是△ABC的中线;AD=DC,BE=EC;DE是△BCD的中线;
故选:A.
13.解:∵AB边上的高是指过顶点C向AB所在直线作的垂线段,
∴在AD⊥BC于D,BE⊥AC于E,CF⊥AB于F,GA⊥AC于A中,只有CF符合上述条件.
故选:D.
14.解:延长CH交AB于点H,
在△ABC中,三边的高交于一点,所以CF⊥AB,
∵∠BAC=75°,且CF⊥AB,
∴∠ACF=15°,
∵∠ACB=60°,
∴∠BCF=45°
在△CDH中,三内角之和为180°,
∴∠CHD=45°,
故答案为∠CHD=45°.
15.解:如图,∵AD是△ABC中线,
∴BD=CD,
∴△ABD周长﹣△ADC的周长=(BA+BD+AD)﹣(AC+AD+CD)=BA﹣AC,
∵△ABD周长与△ADC的周长相差2cm,
∴|BA﹣5|=2,
∴解得BA=7或3.
故答案为:3或7.
16.解:设AC=x,则AB=2x,
∵BD是中线,
∴AD=DC=x,
由题意得,2x+x=30,
解得,x=12,
则AC=12,AB=24,
∴BC=20﹣×12=14.
答:AB=24,BC=14.
17.解:∵BD是中线,
∴AD=CD=AC,
∵△ABD的周长比△BCD的周长大6cm,
∴(AB+AD+BD)﹣(BD+CD+BC)=AB﹣BC=6cm①,
∵△ABC的周长是21cm,AB=AC,
∴2AB+BC=21cm②,
联立①②得:AB=9cm,BC=3cm.
18.解:(1)①∵∠MON=40°,OE平分∠MON,
∴∠AOB=∠BON=20°,
∵AB∥ON,
∴∠ABO=20°,
②∵∠BAD=∠ABD,
∴∠BAD=20°,
∵∠AOB+∠ABO+∠OAB=180°,
∴∠OAC=120°,
∵∠BAD=∠BDA,∠ABO=20°,
∴∠BAD=80°,
∵∠AOB+∠ABO+∠OAB=180°,
∴∠OAC=60°;
故答案为:①20°; ②120,60;
(2)①当点D在线段OB上时,
∵OE是∠MON的角平分线,
∴∠AOB=∠MON=20°,
∵AB⊥OM,
∴∠AOB+∠ABO=90°,
∴∠ABO=70°,
若∠BAD=∠ABD=70°,则x=20
若∠BAD=∠BDA=(180°﹣70°)=55°,则x=35
若∠ADB=∠ABD=70°,则∠BAD=180°﹣2×70°=40°,∴x=50
②当点D在射线BE上时,因为∠ABE=110°,且三角形的内角和为180°,
所以只有∠BAD=∠BDA,此时x=125.
综上可知,存在这样的x的值,使得△ADB中有两个相等的角,
且x=20、35、50、125.
19.解:∵AC=5,DE=2,
∴△ADC的面积为=5,
∵AD是△ABC的中线,
∴△ABD的面积为5,
∴点D到AB的距离是.
故选:A.
20.解:∵由于E、F分别为AD、CE的中点,
∴△ABE、△DBE、△DCE、△AEC的面积相等,
∴S△BEC=2S△BEF=8(cm2),
∴S△ABC=2S△BEC=16(cm2).
故选:D.
21.解:∵AD是△ABC的中线,
∴S△ABD=S△ABC=×18=9,
∵BE是△ABD的中线,
∴S△ABE=S△ABD=×9=4.5.
故选:B.
22.解:∵D为BC的中点,
∴S△ABD=S△ACD=S△ABC,
∵E,F分别是边AD,AC上的中点,
∴S△BDE=S△ABD,S△ADF=S△ADC,S△DEF=S△ADF,
∴S△BDE=S△ABC,S△DEF=S△ADC=S△ABC,
S△BDE+S△DEF=S△ADC+S△ABC=S△ABC,
∴S△ABC=S阴影部分=×3=8.
故选:D.
23.解:①如图1,
当P在AB上时,
∵△APE的面积等于5,
∴x?3=5,
x=;
②当P在BC上时,
∵△APE的面积等于5,
∴S长方形ABCD﹣S△CPE﹣S△ADE﹣S△ABP=5,
∴3×4﹣(3+4﹣x)×2﹣×2×3﹣×4×(x﹣4)=5,
x=5;
③当P在CE上时,
∴(4+3+2﹣x)×3=5,
x=<3+4,此时不符合;
故答案为:或5.
24.解:∵折叠后面积减少,
∴阴影部分的面积占三角形纸的面积的(1﹣﹣)=,
∴三角形纸的面积=50÷=200平方厘米=2平方分米.
故答案为:2.
25.解:加上EF后,原图形中具有△AEF了,故这种做法根据的是三角形的稳定性.
故选:B.
26.解:根据三角形具有稳定性,只要图形分割成了三角形,则具有稳定性.
显然B选项中有四边形,不具有稳定性.
故选:B.
27.解:过八边形的一个顶点作对角线,可以做5条,把八边形分成6个三角形,因为三角形具有稳定性.
故选:C.
28.解:三角形的重心是三条中线的交点,
故选:A.
29.解:∵AD是斜边BC边上的中线,
∴AD=BC=×6=3,
∵G是△ABC重心,
∴=2,
∴AG=AD=×3=2.
故答案为2.
30.解:3+4<8,则3,4,8不能组成三角形,A不符合题意;
5+6=11,则5,6,11不能组成三角形,B不合题意;
5+6>10,则5,6,10能组成三角形,C符合题意;
1+2=3,则1,2,3不能组成三角形,D不合题意,
故选:C.
31.解:连接AB,根据三角形的三边关系定理得:
15﹣10<AB<15+10,
即:5<AB<25,
∴A、B间的距离在5和25之间,
∴A、B间的距离不可能是5米;
故选:A.
32.解:解不等式①,可得x<a,
解不等式②,可得x≥4,
∵不等式组至少有两个整数解,
∴a>5,
又∵存在以3,a,7为边的三角形,
∴4<a<10,
∴a的取值范围是5<a<10,
∴a的整数解有4个,
故选:A.
33.解:∵|a﹣4|+=0,
∴a﹣4=0,a=4;b﹣2=0,b=2;
则4﹣2<c<4+2,
2<c<6,5符合条件;
故选:A.
34.解:设第三边的长为x,
∵三角形两边的长分别是4和10,
∴10﹣4<x<10+4,即6<x<14.
故选:C.
35.解:根据题意得:3x﹣2x<10<3x+2x,
解得:2<x<10.
故答案为:2<x<10.
36.解:因为4﹣2<AC<4+2,
所以2<AC<6,
因为AC长是偶数,
所以AC为4,
故答案为:4.
37.解:∵a、b满足+(b﹣2)2=0,
∴a=9,b=2,
∵a、b、c为三角形的三边,
∴7<c<11,
∵第三边c为奇数,
∴c=9,
故答案为9.
38.解:x2﹣13x+40=0,
(x﹣5)(x﹣8)=0,
所以x1=5,x2=8,
而三角形的两边长分别是3和4,
所以三角形第三边的长为5,
所以三角形的周长为3+4+5=12.
故答案为12.
39.证明:延长ED到H,使DE=DH,连接CH,FH,
∵AD是△ABC的中线,
∴BD=DC,
∵DE、DF分别为∠ADB和∠ADC的平分线,
∴∠1=∠2=∠ADB,∠3=∠4=∠ADC,
∴∠1+∠4=∠2+∠3=∠ADB+∠ADC=×180°=90°,
∵∠1=∠5,
∴∠5+∠4=90°,即∠EDF=∠FDH=90°,
在△EFD和△HFD中,
,
∴△EFD≌△HFD(SAS),
∴EF=FH,
在△BDE和△CDH中,
,
∴△BDE≌△CDH(SAS),
∴BE=CH,
在△CFH中,由三角形三边关系定理得:CF+CH>FH,
∵CH=BE,FH=EF,
∴BE+CF>EF.
40.解:如图,延长AD到E,使DE=AD,
∵AD是BC边上的中线,
∴BD=CD,
在△ABD和△ECD中,,
∴△ABD≌△ECD(SAS),
∴CE=AB,
∵AB=5,AC=3,
∴5﹣3<AE<5+3,
即2<AE<8,
1<AD<4.
故答案为:1<AD<4.
考点一.三角形:
1.如图,图中直角三角形共有( )
A.1个 B.2个 C.3个 D.4个
2.某同学在纸上画了四个点,如果把这四个点彼此连接,连成一个图形,则这个图形中会有 个三角形出现.
3.如图,直角三角形的个数为 .
4.过A、B、C、D、E五个点中任意三点画三角形;
(1)其中以AB为一边可以画出 个三角形;
(2)其中以C为顶点可以画出 个三角形.
考点二.三角形的角平分线、中线和高:
5.用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )
A.B. C.D.
6.以下是四位同学在钝角三角形△ABC中画AC边上的高,其中正确的是( )
A.B.C.D.
7.在数学课上,同学们在练习画边AC上的高时,出现下列四种图形,其中正确的是( )
A.B.C.D.
8.如图,△ABC中,∠BAC是钝角,AD⊥BC、EB⊥BC、FC⊥BC,则下列说法正确的是( )
A.AD是△ABC的高 B.EB是△ABC的高
C.FC是△ABC的高 D.AE、AF是△ABC的高
9.如图,已知P为直线l外一点,点A、B、C、D在直线l上,且PA>PB>PC>PD,下列说法正确的是( )
A.线段PD的长是点P到直线l的距离 B.线段PC可能是△PAB的高
C.线段PD可能是△PBC的高 D.线段PB可能是△PAC的高
10.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等边三角形
11.如图,在四边形ABCD中,AB∥CD,3AB=4AD=6CD,E为AB的中点.萧钟同学用无刻度的直尺先连接CE交BD于点F,再连接AF.则线段AF是△ABD的( )
A.中线 B.高线 C.角平分线 D.中线、高线、角平分线(三线合一)
12.如图,D、E分别是△ABC的边AC、BC的中点,则下列说法不正确的是( )
A.DE是△ABC的中线 B.BD是△ABC的中线
C.AD=DC,BE=EC D.DE是△BCD的中线
13.如图,AD⊥BC于D,BE⊥AC于E,CF⊥AB于F,GA⊥AC于A,在△ABC中,AB边上的高为( )
A.AD B.GA C.BE D.CF
14.如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,AD与BE交于H,则∠CHD= .
15.在△ABC中,AC=5cm,AD是△ABC中线,若△ABD周长与△ADC的周长相差2cm,则BA= cm.
16.如图,在△ABC中(AB>BC),AB=2AC,AC边上中线BD把△ABC的周长分成30和20两部分,求AB和BC的长.
17.如图,△ABC的周长是21cm,AB=AC,中线BD分△ABC为两个三角形,且△ABD的周长比△BCD的周长大6cm,求AB,BC.
18.已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则
①∠ABO的度数是 ;
②当∠BAD=∠ABD时,x= ;当∠BAD=∠BDA时,x= .
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
考点三.三角形的面积:
19.如图,AD是△ABC的中线,DE是△ADC的高线,AB=3,AC=5,DE=2,那么点D到AB的距离是( )
A. B. C. D.2
20.如图,在△ABC中,已知点E、F分别是AD、CE边上的中点,且S△BEF=4cm2,则S△ABC的值为( )
A.1cm2 B.2cm2 C.8cm2 D.16cm2
21.已知AD是△ABC的中线,BE是△ABD的中线,若△ABC的面积为18,则△ABE的面积为( )
A.5 B.4.5
C.4 D.9
22.如图,D,E,F分别是边BC,AD,AC上的中点,若S四边形的面积为3,则△ABC的面积是( )
A.5 B.6 C.7 D.8
23.如图,长方形ABCD中,AB=4cm,BC=3cm,点E是CD的中点,动点P从A点出发,以每秒1cm的速度沿A→B→C→E运动,最终到达点E.若点P运动的时间为x秒,那么当x= 时,△APE的面积等于5.
24.把一张三角形的纸折叠成如图后,面积减少,已知阴影部分的面积是50平方厘米,则这张三角形纸的面积是 平方分米.
考点四.三角形的稳定性:
25.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
A.两点之间的线段最短 B.三角形具有稳定性
C.长方形是轴对称图形 D.长方形的四个角都是直角
26.下列图形中不具有稳定性是( )
A.B.C.D.
27.用八根木条钉成如图所示的八边形木架,要使它不变形,至少要钉上木条的根数是( )
A.3根 B.4根 C.5根 D.6根
考点五.三角形的重心:
28.三角形的重心是( )
A.三角形三条边上中线的交点 B.三角形三条边上高线的交点
C.三角形三条边垂直平分线的交点 D.三角形三条内角平分线的交点
29.在Rt△ABC中,AD是斜边BC边上的中线,G是△ABC重心,如果BC=6,那么线段AG的长为 .
考点六.三角形三边关系:
30.下列长度的三条线段能组成三角形的是( )
A.3,4,8 B.5,6,11 C.5,6,10 D.1,2,3
31.如图,为估计池塘岸边A、B两点的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是( )
A.5米 B.10米 C.15米 D.20米
32.已知关于x的不等式组至少有两个整数解,且存在以3,a,7为边的三角形,则a的整数解有( )
A.4个 B.5个 C.6个 D.7个
33.若a、b、c为△ABC的三边长,且满足|a﹣4|+=0,则c的值可以为( )
A.5 B.6 C.7 D.8
34.已知三角形两边的长分别是4和10,则此三角形第三边的长可能是( )
A.5 B.6 C.12 D.16
35.△ABC中,AB=10,BC=2x,AC=3x,则x的取值范围 .
36.在△ABC中,若AB=4,BC=2,且AC的长为偶数,则AC= .
37.若a、b、c为三角形的三边,且a、b满足+(b﹣2)2=0,第三边c为奇数,则c= .
38.三角形的两边长分别是3和4,第三边长是方程x2﹣13x+40=0的根,则该三角形的周长为 .
39.如图:已知AD为△ABC的中线,且∠1=∠2,∠3=∠4,求证:BE+CF>EF.
40.在△ABC中,AB=5,AC=3,AD是BC边上的中线,则AD的取值范围是 .
参考答案
1.解:如图,图中直角三角形有Rt△ABD、Rt△BDC、Rt△ABC,共有3个,
故选:C.
2.解:∵①当四个点共线时,不能作出三角形;
②当三个点共线,第四个点不在这条直线上时,能够画出3个三角形;
③若4个点能构成凹四边形,则能画出4个三角形;
④当任意的三个点不共线时,则能够画出8个三角形.
∴0或3或4或8.
3.解:如图,直角三角形有:△ADC、△BCD、△CDE、△BDE、△ACE、△ACB,一共6个,
故答案为:6.
4.解:(1)如图,以AB为一边的三角形有△ABC、△ABD、△ABE共3个;
(2)如图,以点C为顶点的三角形有△ABC、△BEC、△BCD、△ACE、△ACD、△CDE共6个.
故答案为:(1)3,(2)6.
5.解:B,C,D都不是△ABC的边BC上的高,
故选:A.
6.解:A、高BD交AC的延长线于点D处,符合题意;
B、没有经过顶点B,不符合题意;
C、做的是BC边上的高线AD,不符合题意;
D、没有经过顶点B,不符合题意.
故选:A.
7.解:AC边上的高应该是过B作垂线段AC,符合这个条件的是C;
A,B,D都不过B点,故错误;
故选:C.
8.解:△ABC中,画BC边上的高,是线段AD.
故选:A.
9.解:A.线段PD的长不一定是点P到直线l的距离,故本选项错误;
B.线段PC不可能是△PAB的高,故本选项错误;
C.线段PD可能是△PBC的高,故本选项正确;
D.线段PB不可能是△PAC的高,故本选项错误;
故选:C.
10.解:一个三角形的三条高的交点恰是三角形的一个顶点,这个三角形是直角三角形.
故选:C.
11.解:∵3AB=6CD,E为AB的中点,
∴CD=AB,BE=AB,
∴CD=BE,
又∵AB∥CD,
∴∠EBF=∠CDF,
又∵∠EFB=∠CFD,
∴△BEF≌△DCF(AAS),
∴BF=DF,
∴线段AF是△ABD的中线,
故选:A.
12.解:∵D、E分别是△ABC的边AC、BC的中点,
∴DE是△ABC的中位线,不是中线;BD是△ABC的中线;AD=DC,BE=EC;DE是△BCD的中线;
故选:A.
13.解:∵AB边上的高是指过顶点C向AB所在直线作的垂线段,
∴在AD⊥BC于D,BE⊥AC于E,CF⊥AB于F,GA⊥AC于A中,只有CF符合上述条件.
故选:D.
14.解:延长CH交AB于点H,
在△ABC中,三边的高交于一点,所以CF⊥AB,
∵∠BAC=75°,且CF⊥AB,
∴∠ACF=15°,
∵∠ACB=60°,
∴∠BCF=45°
在△CDH中,三内角之和为180°,
∴∠CHD=45°,
故答案为∠CHD=45°.
15.解:如图,∵AD是△ABC中线,
∴BD=CD,
∴△ABD周长﹣△ADC的周长=(BA+BD+AD)﹣(AC+AD+CD)=BA﹣AC,
∵△ABD周长与△ADC的周长相差2cm,
∴|BA﹣5|=2,
∴解得BA=7或3.
故答案为:3或7.
16.解:设AC=x,则AB=2x,
∵BD是中线,
∴AD=DC=x,
由题意得,2x+x=30,
解得,x=12,
则AC=12,AB=24,
∴BC=20﹣×12=14.
答:AB=24,BC=14.
17.解:∵BD是中线,
∴AD=CD=AC,
∵△ABD的周长比△BCD的周长大6cm,
∴(AB+AD+BD)﹣(BD+CD+BC)=AB﹣BC=6cm①,
∵△ABC的周长是21cm,AB=AC,
∴2AB+BC=21cm②,
联立①②得:AB=9cm,BC=3cm.
18.解:(1)①∵∠MON=40°,OE平分∠MON,
∴∠AOB=∠BON=20°,
∵AB∥ON,
∴∠ABO=20°,
②∵∠BAD=∠ABD,
∴∠BAD=20°,
∵∠AOB+∠ABO+∠OAB=180°,
∴∠OAC=120°,
∵∠BAD=∠BDA,∠ABO=20°,
∴∠BAD=80°,
∵∠AOB+∠ABO+∠OAB=180°,
∴∠OAC=60°;
故答案为:①20°; ②120,60;
(2)①当点D在线段OB上时,
∵OE是∠MON的角平分线,
∴∠AOB=∠MON=20°,
∵AB⊥OM,
∴∠AOB+∠ABO=90°,
∴∠ABO=70°,
若∠BAD=∠ABD=70°,则x=20
若∠BAD=∠BDA=(180°﹣70°)=55°,则x=35
若∠ADB=∠ABD=70°,则∠BAD=180°﹣2×70°=40°,∴x=50
②当点D在射线BE上时,因为∠ABE=110°,且三角形的内角和为180°,
所以只有∠BAD=∠BDA,此时x=125.
综上可知,存在这样的x的值,使得△ADB中有两个相等的角,
且x=20、35、50、125.
19.解:∵AC=5,DE=2,
∴△ADC的面积为=5,
∵AD是△ABC的中线,
∴△ABD的面积为5,
∴点D到AB的距离是.
故选:A.
20.解:∵由于E、F分别为AD、CE的中点,
∴△ABE、△DBE、△DCE、△AEC的面积相等,
∴S△BEC=2S△BEF=8(cm2),
∴S△ABC=2S△BEC=16(cm2).
故选:D.
21.解:∵AD是△ABC的中线,
∴S△ABD=S△ABC=×18=9,
∵BE是△ABD的中线,
∴S△ABE=S△ABD=×9=4.5.
故选:B.
22.解:∵D为BC的中点,
∴S△ABD=S△ACD=S△ABC,
∵E,F分别是边AD,AC上的中点,
∴S△BDE=S△ABD,S△ADF=S△ADC,S△DEF=S△ADF,
∴S△BDE=S△ABC,S△DEF=S△ADC=S△ABC,
S△BDE+S△DEF=S△ADC+S△ABC=S△ABC,
∴S△ABC=S阴影部分=×3=8.
故选:D.
23.解:①如图1,
当P在AB上时,
∵△APE的面积等于5,
∴x?3=5,
x=;
②当P在BC上时,
∵△APE的面积等于5,
∴S长方形ABCD﹣S△CPE﹣S△ADE﹣S△ABP=5,
∴3×4﹣(3+4﹣x)×2﹣×2×3﹣×4×(x﹣4)=5,
x=5;
③当P在CE上时,
∴(4+3+2﹣x)×3=5,
x=<3+4,此时不符合;
故答案为:或5.
24.解:∵折叠后面积减少,
∴阴影部分的面积占三角形纸的面积的(1﹣﹣)=,
∴三角形纸的面积=50÷=200平方厘米=2平方分米.
故答案为:2.
25.解:加上EF后,原图形中具有△AEF了,故这种做法根据的是三角形的稳定性.
故选:B.
26.解:根据三角形具有稳定性,只要图形分割成了三角形,则具有稳定性.
显然B选项中有四边形,不具有稳定性.
故选:B.
27.解:过八边形的一个顶点作对角线,可以做5条,把八边形分成6个三角形,因为三角形具有稳定性.
故选:C.
28.解:三角形的重心是三条中线的交点,
故选:A.
29.解:∵AD是斜边BC边上的中线,
∴AD=BC=×6=3,
∵G是△ABC重心,
∴=2,
∴AG=AD=×3=2.
故答案为2.
30.解:3+4<8,则3,4,8不能组成三角形,A不符合题意;
5+6=11,则5,6,11不能组成三角形,B不合题意;
5+6>10,则5,6,10能组成三角形,C符合题意;
1+2=3,则1,2,3不能组成三角形,D不合题意,
故选:C.
31.解:连接AB,根据三角形的三边关系定理得:
15﹣10<AB<15+10,
即:5<AB<25,
∴A、B间的距离在5和25之间,
∴A、B间的距离不可能是5米;
故选:A.
32.解:解不等式①,可得x<a,
解不等式②,可得x≥4,
∵不等式组至少有两个整数解,
∴a>5,
又∵存在以3,a,7为边的三角形,
∴4<a<10,
∴a的取值范围是5<a<10,
∴a的整数解有4个,
故选:A.
33.解:∵|a﹣4|+=0,
∴a﹣4=0,a=4;b﹣2=0,b=2;
则4﹣2<c<4+2,
2<c<6,5符合条件;
故选:A.
34.解:设第三边的长为x,
∵三角形两边的长分别是4和10,
∴10﹣4<x<10+4,即6<x<14.
故选:C.
35.解:根据题意得:3x﹣2x<10<3x+2x,
解得:2<x<10.
故答案为:2<x<10.
36.解:因为4﹣2<AC<4+2,
所以2<AC<6,
因为AC长是偶数,
所以AC为4,
故答案为:4.
37.解:∵a、b满足+(b﹣2)2=0,
∴a=9,b=2,
∵a、b、c为三角形的三边,
∴7<c<11,
∵第三边c为奇数,
∴c=9,
故答案为9.
38.解:x2﹣13x+40=0,
(x﹣5)(x﹣8)=0,
所以x1=5,x2=8,
而三角形的两边长分别是3和4,
所以三角形第三边的长为5,
所以三角形的周长为3+4+5=12.
故答案为12.
39.证明:延长ED到H,使DE=DH,连接CH,FH,
∵AD是△ABC的中线,
∴BD=DC,
∵DE、DF分别为∠ADB和∠ADC的平分线,
∴∠1=∠2=∠ADB,∠3=∠4=∠ADC,
∴∠1+∠4=∠2+∠3=∠ADB+∠ADC=×180°=90°,
∵∠1=∠5,
∴∠5+∠4=90°,即∠EDF=∠FDH=90°,
在△EFD和△HFD中,
,
∴△EFD≌△HFD(SAS),
∴EF=FH,
在△BDE和△CDH中,
,
∴△BDE≌△CDH(SAS),
∴BE=CH,
在△CFH中,由三角形三边关系定理得:CF+CH>FH,
∵CH=BE,FH=EF,
∴BE+CF>EF.
40.解:如图,延长AD到E,使DE=AD,
∵AD是BC边上的中线,
∴BD=CD,
在△ABD和△ECD中,,
∴△ABD≌△ECD(SAS),
∴CE=AB,
∵AB=5,AC=3,
∴5﹣3<AE<5+3,
即2<AE<8,
1<AD<4.
故答案为:1<AD<4.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
