【课时作业】3.8圆内接正多边形(含答案)
文档属性
| 名称 | 【课时作业】3.8圆内接正多边形(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 250.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 17:13:40 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2020-2021学年九年级数学下册课时作业(北师版)
第三章 圆
8 圆内接正多边形
一、选择题
1.正六边形的边长等于2,则这个正六边形的面积等于( )
A.4 B.6 C.7 D.8
2.从一个正五边形的一个顶点出发的两条对角线的夹角为( )
A.30° B.36° C.50° D.72°
3.若一个正多边形的外角大于它的一个内角,则它的边数为( )
A.3 B.4 C.5 D.6
4.边长与外接圆半径相等的正多边形是( )
A.正三角形 B.正方形 C.正六边形 D.正八边形
5.下列说法正确的是( )
A.各边相等的多边形是正多边形
B.圆内接菱形是正方形
C.各角相等的圆内接多边形是正多边形
D.正多边形都是中心对称图形
6.用量角器将圆五等分,得到正五边形ABCDE(如图),AC,BD相交于点P,∠APB等于( )
A.36° B.60° C.72° D.108°
7.已知四边形ABCD内接于⊙O,给出下列三个条件:①===;②AB=BC=CD=DA;③∠A=∠B=∠C=∠D.则在这些条件中,能够判定四边形ABCD是正方形的条件共有( )
A.0个 B.1个 C.2个 D.3个
8.如图,在正六边形ABCDEF中,AC=2,则它的边长是( )
A.1 B. C. D.2
9.以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A. B. C. D.
二、填空题
10.一个外角等于它的一个内角的正多边形是__________.
11.正多边形中,当中心角为15°时,边数为______条.
12.如果要画一个正十二边形,那么用量角器将圆________等分,每一份的圆心角是______.
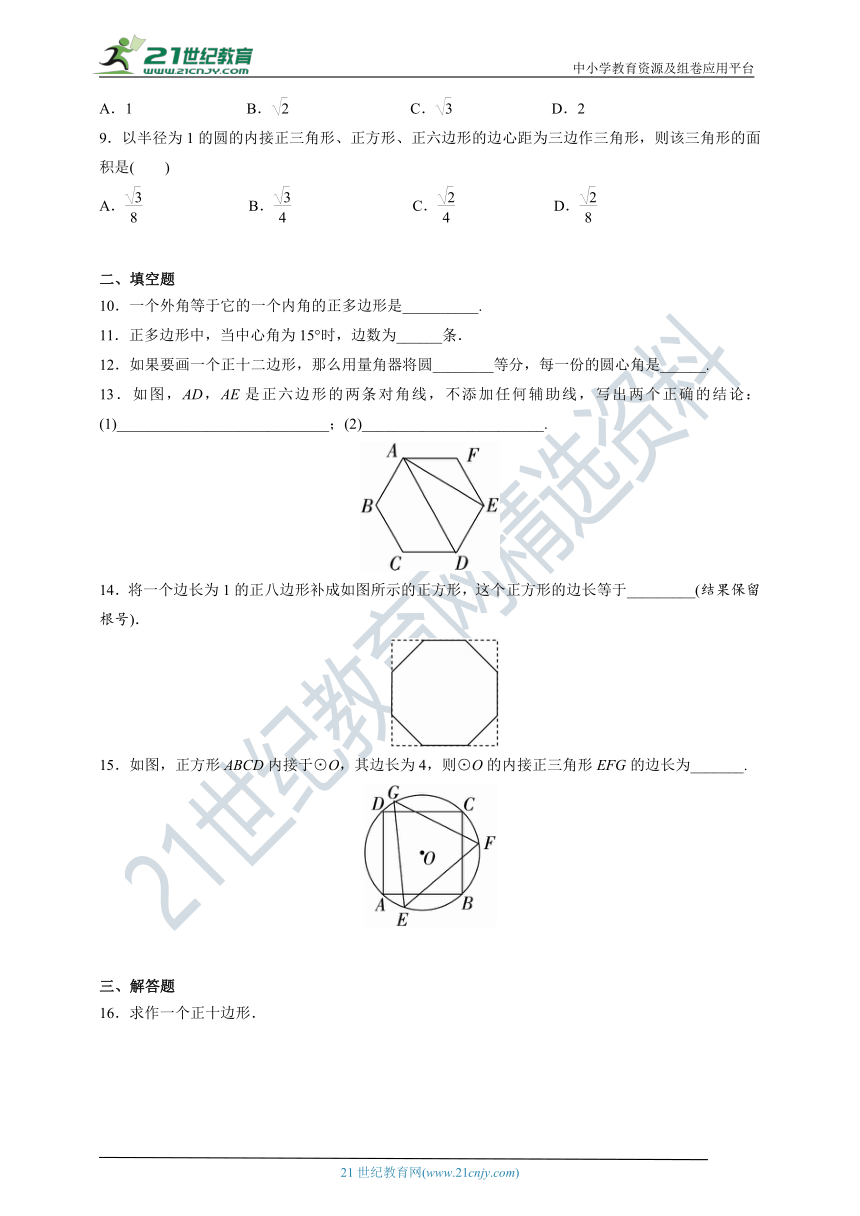
13.如图,AD,AE是正六边形的两条对角线,不添加任何辅助线,写出两个正确的结论:(1)____________________________;(2)________________________.
14.将一个边长为1的正八边形补成如图所示的正方形,这个正方形的边长等于_________(结果保留根号).
15.如图,正方形ABCD内接于⊙O,其边长为4,则⊙O的内接正三角形EFG的边长为_______.
三、解答题
16.求作一个正十边形.
17.已知两个正多边形的边数之比为2∶1,而它们的内角和之比为8∶3.求这两个正多边形的边数.
18.如图,已知⊙O的周长等于12πcm,求以它的半径为边长的正六边形ABCDEF的面积.
19.如图,AB,PA是⊙O内接正n边形的相邻两边,切线PM与BA的延长线相交于点M,∠PMB=112.5°,求边数n.
20.如图,有一个圆O和两个正六边形T1,T2.T1的6个顶点都在圆周上,T2的6条边都和⊙O相切(我们称T1,T2分别为圆O的内接正六边形和外切正六边形).
(1)设T1,T2的边长分别为a,b,⊙O的半径为r,求r∶a及r∶b的值;
(2)求正六边形T1,T2的面积比S1∶S2的值.
参 考 答 案
1. B 2. B 3. A 4. C 5. B 6. C 7. C 8. D 9. D
10. 正方形
11. 24
12. 十二 30°
13. (1)四边形ABCD是等腰梯形 (2)△AEF是等腰三角形
14. +1
15. 2
16. 解:作法:(1)如图,画⊙O,作半径OA. (2)以O为顶点,OA为一边作∠AOB=36°,边OB交⊙O于点B. (3)以B为圆心,AB为半径画弧,交⊙O于点C,以C为圆心,AB为半径画弧,交⊙O于点D;顺次画弧,得到分点E,F,G,H,I,J. (4)顺次连接各分点.多边形ABCDEFGHIJ就是所求的正十边形.如图所示.
17. 解:设这两个正多边形的边数为2x,x,根据题意,得180(2x-2)∶180(x-2)=8∶3,所以x=5,2x=10.即这两个正多边形的边数为10,5.
18. 解:连接OA,OB.过点O作OM⊥AB于点M.∵六边形ABCDEF是正六边形,∴∠AOB=60°.又∵OA=OB,∴△OAB是等边三角形.∵⊙O的周长为12πcm,∴2πr=12π.∴r=6cm,∴AB=6cm.∵=,∴OM=3cm.∴S△OAB=×6×3=9(cm2).∴正六边形ABCDEF的面积为S正六边形ABCDEF=9×6=54(cm2).
19. 解:连接OP,OA,则OP⊥PM,∠OAP=∠OPA=∠PAB,又∠PAB=∠PMA+∠MPA,所以∠PAB=112.5°+90°-∠PAB,得∠PAB=135°,所以135°n=(n-2)×180°,解得n=8.
20. 解:(1)连接圆心O和T1的6个顶点可得6个全等的正三角形.所以r∶a=1∶1;连接圆心O和T2相邻的两个顶点,得以⊙O半径为高的正三角形,所以r∶b=∶2.
(2)T1∶T2的边长比是∶2,所以S1∶S2=(a∶b)2=3∶4.
_21?????????è?????(www.21cnjy.com)_
2020-2021学年九年级数学下册课时作业(北师版)
第三章 圆
8 圆内接正多边形
一、选择题
1.正六边形的边长等于2,则这个正六边形的面积等于( )
A.4 B.6 C.7 D.8
2.从一个正五边形的一个顶点出发的两条对角线的夹角为( )
A.30° B.36° C.50° D.72°
3.若一个正多边形的外角大于它的一个内角,则它的边数为( )
A.3 B.4 C.5 D.6
4.边长与外接圆半径相等的正多边形是( )
A.正三角形 B.正方形 C.正六边形 D.正八边形
5.下列说法正确的是( )
A.各边相等的多边形是正多边形
B.圆内接菱形是正方形
C.各角相等的圆内接多边形是正多边形
D.正多边形都是中心对称图形
6.用量角器将圆五等分,得到正五边形ABCDE(如图),AC,BD相交于点P,∠APB等于( )
A.36° B.60° C.72° D.108°
7.已知四边形ABCD内接于⊙O,给出下列三个条件:①===;②AB=BC=CD=DA;③∠A=∠B=∠C=∠D.则在这些条件中,能够判定四边形ABCD是正方形的条件共有( )
A.0个 B.1个 C.2个 D.3个
8.如图,在正六边形ABCDEF中,AC=2,则它的边长是( )
A.1 B. C. D.2
9.以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A. B. C. D.
二、填空题
10.一个外角等于它的一个内角的正多边形是__________.
11.正多边形中,当中心角为15°时,边数为______条.
12.如果要画一个正十二边形,那么用量角器将圆________等分,每一份的圆心角是______.
13.如图,AD,AE是正六边形的两条对角线,不添加任何辅助线,写出两个正确的结论:(1)____________________________;(2)________________________.
14.将一个边长为1的正八边形补成如图所示的正方形,这个正方形的边长等于_________(结果保留根号).
15.如图,正方形ABCD内接于⊙O,其边长为4,则⊙O的内接正三角形EFG的边长为_______.
三、解答题
16.求作一个正十边形.
17.已知两个正多边形的边数之比为2∶1,而它们的内角和之比为8∶3.求这两个正多边形的边数.
18.如图,已知⊙O的周长等于12πcm,求以它的半径为边长的正六边形ABCDEF的面积.
19.如图,AB,PA是⊙O内接正n边形的相邻两边,切线PM与BA的延长线相交于点M,∠PMB=112.5°,求边数n.
20.如图,有一个圆O和两个正六边形T1,T2.T1的6个顶点都在圆周上,T2的6条边都和⊙O相切(我们称T1,T2分别为圆O的内接正六边形和外切正六边形).
(1)设T1,T2的边长分别为a,b,⊙O的半径为r,求r∶a及r∶b的值;
(2)求正六边形T1,T2的面积比S1∶S2的值.
参 考 答 案
1. B 2. B 3. A 4. C 5. B 6. C 7. C 8. D 9. D
10. 正方形
11. 24
12. 十二 30°
13. (1)四边形ABCD是等腰梯形 (2)△AEF是等腰三角形
14. +1
15. 2
16. 解:作法:(1)如图,画⊙O,作半径OA. (2)以O为顶点,OA为一边作∠AOB=36°,边OB交⊙O于点B. (3)以B为圆心,AB为半径画弧,交⊙O于点C,以C为圆心,AB为半径画弧,交⊙O于点D;顺次画弧,得到分点E,F,G,H,I,J. (4)顺次连接各分点.多边形ABCDEFGHIJ就是所求的正十边形.如图所示.
17. 解:设这两个正多边形的边数为2x,x,根据题意,得180(2x-2)∶180(x-2)=8∶3,所以x=5,2x=10.即这两个正多边形的边数为10,5.
18. 解:连接OA,OB.过点O作OM⊥AB于点M.∵六边形ABCDEF是正六边形,∴∠AOB=60°.又∵OA=OB,∴△OAB是等边三角形.∵⊙O的周长为12πcm,∴2πr=12π.∴r=6cm,∴AB=6cm.∵=,∴OM=3cm.∴S△OAB=×6×3=9(cm2).∴正六边形ABCDEF的面积为S正六边形ABCDEF=9×6=54(cm2).
19. 解:连接OP,OA,则OP⊥PM,∠OAP=∠OPA=∠PAB,又∠PAB=∠PMA+∠MPA,所以∠PAB=112.5°+90°-∠PAB,得∠PAB=135°,所以135°n=(n-2)×180°,解得n=8.
20. 解:(1)连接圆心O和T1的6个顶点可得6个全等的正三角形.所以r∶a=1∶1;连接圆心O和T2相邻的两个顶点,得以⊙O半径为高的正三角形,所以r∶b=∶2.
(2)T1∶T2的边长比是∶2,所以S1∶S2=(a∶b)2=3∶4.
_21?????????è?????(www.21cnjy.com)_
