第28章概率初步水平测试
图片预览

文档简介
沪科九年级下册第28章概率初步水平测试
一、选择题(每小题3分,共24分)
1.下列说法正确的是( )
A.一颗质地均匀的骰子已连续抛掷了次,其中,抛掷出点的次数最少,则第次一定抛掷出点
B.某种彩票中奖的概率是,因此买张该种彩票一定会中奖
C.天气预报说明天下雨的概率是,所以明天将有一半时间在下雨
D.抛掷一枚图钉,钉尖触地和钉尖朝上的概率不相等
2.某电视台举行歌手大奖赛,每场比赛都有编号为1~10号共10道综合素质测试题供选手随机抽取作答.在某场比赛中,前两位选手分别抽走了2号,7号题,第3位选手抽中8号题的概率是( )
A. B. C. D. HYPERLINK "http://www./Index.html" EMBED Equation.DSMT4
3.从某班学生中随机选取一名学生是女生的概率为,则该班女生与男生的人数比是( )
A. B. C. HYPERLINK "http://www./Index.html" EMBED Equation.DSMT4 D.
4.小明在做一道正确答案是2的计算题时,由于运算符号(“+”、“-”、“×”或“÷”)被墨迹污染,看见的算式是“4■2”,那么小明还能做对的概率是( ).
A. B. C. D.
2.在元旦游园晚会上有一个闯关活动:将5张分别画有等腰梯形、圆、平行四边形、等腰三角形、菱形的卡片任意摆放,将有图形的一面朝下,从中任意翻开一张,如果翻开的图形是轴对称图形,就可以过关.那么一次过关的概率是( )
A. B. HYPERLINK "http://www./Index.html" C. D.
6.某市电视台在今年5月举办的“开心就唱”歌手大赛活动中,号召观众发短信为参赛者投支持票,投票短信每1万条为1组,每组抽出1个一等奖,3个二等奖,6个三等奖.张艺同学发了1条短信,她的获奖概率是( )
A. HYPERLINK "http://www./Index.html" EMBED Equation.DSMT4 B. C. D.
7. 在拼图游戏中,从图1的四张纸片中,任取两张纸片,能拼成“小房子”(如图2)的概率等于( ).
A. 1 B. C. D.
8. 投掷一枚普通的正方体骰子,四位同学各自发表了以下见解:
①出现“点数为奇数”的概率等于出现“点数为偶数”的概率.
②只要连掷6次,一定会“出现一点”.
③投掷前默念几次“出现6点”,投掷结果“出现6点”的可能性就会加大.
④连续投掷3次,出现的点数之和不可能等于19.
其中正确的见解有 ( ).
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题4分,共24分)
9.根据天气预报,明天降水概率为,后天降水概率为 HYPERLINK "http://www./Index.html" EMBED Equation.DSMT4 ,假如你准备明天或后天去放风筝,你选择 天为佳.
10.在掷一枚硬币的试验中,着地时反面向上的概率为.如果掷一枚硬币150次,则着地时正面向上约 次.
11.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色其他外完全相同,小李通过多次摸球试验后发现其中摸到红色、黑色球的频率分别为15%和45%,则口袋中白色球的数目很可能是_________.
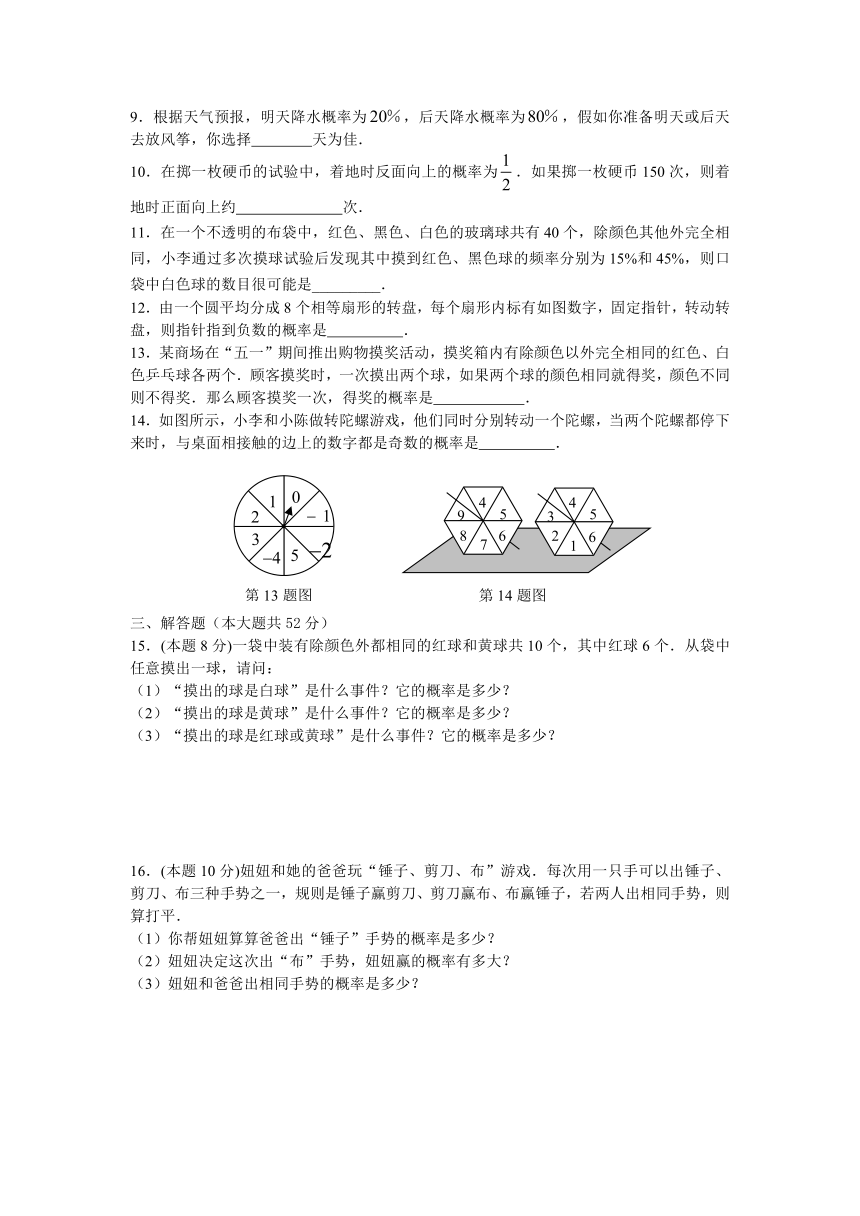
12.由一个圆平均分成8个相等扇形的转盘,每个扇形内标有如图数字,固定指针,转动转盘,则指针指到负数的概率是 .
13.某商场在“五一”期间推出购物摸奖活动,摸奖箱内有除颜色以外完全相同的红色、白色乒乓球各两个.顾客摸奖时,一次摸出两个球,如果两个球的颜色相同就得奖,颜色不同则不得奖.那么顾客摸奖一次,得奖的概率是 .
14.如图所示,小李和小陈做转陀螺游戏,他们同时分别转动一个陀螺,当两个陀螺都停下来时,与桌面相接触的边上的数字都是奇数的概率是 .
三、解答题(本大题共52分)
15.(本题8分)一袋中装有除颜色外都相同的红球和黄球共10个,其中红球6个.从袋中任意摸出一球,请问:
(1)“摸出的球是白球”是什么事件?它的概率是多少?
(2)“摸出的球是黄球”是什么事件?它的概率是多少?
(3)“摸出的球是红球或黄球”是什么事件?它的概率是多少?
16.(本题10分)妞妞和她的爸爸玩“锤子、剪刀、布”游戏.每次用一只手可以出锤子、剪刀、布三种手势之一,规则是锤子赢剪刀、剪刀赢布、布赢锤子,若两人出相同手势,则算打平.
(1)你帮妞妞算算爸爸出“锤子”手势的概率是多少?
(2)妞妞决定这次出“布”手势,妞妞赢的概率有多大?
(3)妞妞和爸爸出相同手势的概率是多少?
17.(本题10分)桌面上放有张卡片,正面分别标有数字,,,.这些卡片除数字外完全相同,把这些卡片反面朝上洗匀后放在桌面上,甲从中任意抽出一张,记下卡片上的数字后仍反面朝上放回洗匀,乙也从中任意抽出一张,记下卡片上的数字,然后将这两数相加.
(1)请用列表或画树形图的方法求两数之和为的概率.
(2)若甲与乙按上述方式做游戏,当两数之和为时,甲胜;反之则乙胜.若甲胜一次得分,那么乙胜一次得多少分,这个游戏对双方公平?
18.(本题12分)“六一”儿童节,小明与小亮受邀到科技馆担任义务讲解员,他们俩各自独立从A区(时代辉煌)、B区(科学启迪)、C区(智慧之光)、D区(儿童世界)这四个主题展区中随机选择一个为参观者服务.
(1)请用列表法或画树状图法说明当天小明与小亮出现在各主题展区担任义务讲解员的所有可能情况.(用字母表示)
(2)求小明与小亮只单独出现在B区(科学启迪)、C区(智慧之光)、D区(儿童世界)三个主题展区中担任义务讲解员的概率.
19、(本题12分)七巧板是我国流传已久的一种智力玩具,小鹏在玩七巧板时用它画成了3副图案并将它们贴在3张完全相同的不透明卡片上,如图.小鹏将这3张卡片背面朝上洗匀后放在桌子上,从中随机抽取一张,放回后洗匀,再随机抽取一张卡片.请你用列表法或画树状图(树形图)法,帮助小鹏求出两张卡片上的图案都是小动物的概率.(卡片名称可用字母表示)
四、附加题(本题为综合题,共20分)
20、在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只, 某学习小组做摸球实验, 将球搅匀后从中随机摸出一个球记下颜色, 再把它放回袋中, 不断重复. 下表是活动进行中的一组统计数据:
摸球的次数 100 150 200 500 800 1000
摸到白球的次数 58 96 116 295 484 601
摸到白球的频率 0.58 0.64 0.58 0.59 0.605 0.601
⑴ 请估计:当很大时, 摸到白球的频率将会接近 ;
⑵ 假如你去摸一次, 你摸到白球的概率是 , 摸到黑球的概率是 ;
⑶ 试估算口袋中黑、白两种颜色的球各有多少只
⑷ 解决了上面的问题, 小明同学猛然顿悟, 过去一个悬而未决的问题有办法了. 这个问题是: 在一个不透明的口袋里装有若干个白球, 在不允许将球倒出来数的情况下, 如何估计白球的个数(可以借助其他工具及用品) 请你应用统计与概率的思想和方法解决这个问题,写出解决这个问题的主要步骤及估算方法.
参考答案
1.D
2.C
3.B
4.A
5.D
6.B
7.D
8.B
9.明天
10.75
11.16
12.
13.
14.
15(1)“摸出的球是白球”是不可能事件,它的概率为;(2)“摸出的球是黄球”是不确定事件,它的概率为;(3)“摸出的球是红球或黄球”是必然事件,它的概率为.
16(1);(2);(3)
17(1)由列表(略)可得:(数字之和为) HYPERLINK "http://www./Index.html" EMBED Equation.DSMT4;
(2)因为(甲胜),(乙胜),甲胜一次得分,要使这个游戏对双方公平,乙胜一次的得分应为:分
18(1)(1)当天小明与小亮出现在各主题展区担任义务讲解员的所有可能情况画树形图如下:
(2)小明与小亮只单独出现在区(科学启迪)、区(智慧之光)、区(儿童世界)三个主题展区中担任义务讲解员的情况有
6种,故所求概率为
19解:列表得 或画树状图(树形图)得
A B C
A (A,A) (A,B) (A,C)
B (B,A) (B,B) (B,C)
C (C,A) (C,B) (C,C)
由表格(或画树状图/树形图)可知,共有9种等可能性结果,其中两张卡片上的图案都是小动物的结果有4种.
∴P(两张卡片上的图案都是小动物)=.
四、20.(1)0.6;(2)0.6;0.4;(3)黑球8个,白球12个;
(4)①先从不透明的口袋里摸出个白球,都涂上颜色(如黑色),然后放回口袋里,搅拌均匀;②将搅匀后的球从中随机摸出一个球记下颜色, 再把它放回袋中, 不断大量重复次,记录摸出黑球频数为;③根据用频数估计概率的方法可得出白球数为.
第13题图
4
5
6
7
8
9
4
5
6
1
2
3
第14题图
狐狸
A
兔子
C
小屋
B
A
A
B
C
D
B
A
B
C
D
C
A
B
C
D
D
A
B
C
D
第22题答案图
小明
小亮
第
二
张
第
一
张
一、选择题(每小题3分,共24分)
1.下列说法正确的是( )
A.一颗质地均匀的骰子已连续抛掷了次,其中,抛掷出点的次数最少,则第次一定抛掷出点
B.某种彩票中奖的概率是,因此买张该种彩票一定会中奖
C.天气预报说明天下雨的概率是,所以明天将有一半时间在下雨
D.抛掷一枚图钉,钉尖触地和钉尖朝上的概率不相等
2.某电视台举行歌手大奖赛,每场比赛都有编号为1~10号共10道综合素质测试题供选手随机抽取作答.在某场比赛中,前两位选手分别抽走了2号,7号题,第3位选手抽中8号题的概率是( )
A. B. C. D. HYPERLINK "http://www./Index.html" EMBED Equation.DSMT4
3.从某班学生中随机选取一名学生是女生的概率为,则该班女生与男生的人数比是( )
A. B. C. HYPERLINK "http://www./Index.html" EMBED Equation.DSMT4 D.
4.小明在做一道正确答案是2的计算题时,由于运算符号(“+”、“-”、“×”或“÷”)被墨迹污染,看见的算式是“4■2”,那么小明还能做对的概率是( ).
A. B. C. D.
2.在元旦游园晚会上有一个闯关活动:将5张分别画有等腰梯形、圆、平行四边形、等腰三角形、菱形的卡片任意摆放,将有图形的一面朝下,从中任意翻开一张,如果翻开的图形是轴对称图形,就可以过关.那么一次过关的概率是( )
A. B. HYPERLINK "http://www./Index.html" C. D.
6.某市电视台在今年5月举办的“开心就唱”歌手大赛活动中,号召观众发短信为参赛者投支持票,投票短信每1万条为1组,每组抽出1个一等奖,3个二等奖,6个三等奖.张艺同学发了1条短信,她的获奖概率是( )
A. HYPERLINK "http://www./Index.html" EMBED Equation.DSMT4 B. C. D.
7. 在拼图游戏中,从图1的四张纸片中,任取两张纸片,能拼成“小房子”(如图2)的概率等于( ).
A. 1 B. C. D.
8. 投掷一枚普通的正方体骰子,四位同学各自发表了以下见解:
①出现“点数为奇数”的概率等于出现“点数为偶数”的概率.
②只要连掷6次,一定会“出现一点”.
③投掷前默念几次“出现6点”,投掷结果“出现6点”的可能性就会加大.
④连续投掷3次,出现的点数之和不可能等于19.
其中正确的见解有 ( ).
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题4分,共24分)
9.根据天气预报,明天降水概率为,后天降水概率为 HYPERLINK "http://www./Index.html" EMBED Equation.DSMT4 ,假如你准备明天或后天去放风筝,你选择 天为佳.
10.在掷一枚硬币的试验中,着地时反面向上的概率为.如果掷一枚硬币150次,则着地时正面向上约 次.
11.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色其他外完全相同,小李通过多次摸球试验后发现其中摸到红色、黑色球的频率分别为15%和45%,则口袋中白色球的数目很可能是_________.
12.由一个圆平均分成8个相等扇形的转盘,每个扇形内标有如图数字,固定指针,转动转盘,则指针指到负数的概率是 .
13.某商场在“五一”期间推出购物摸奖活动,摸奖箱内有除颜色以外完全相同的红色、白色乒乓球各两个.顾客摸奖时,一次摸出两个球,如果两个球的颜色相同就得奖,颜色不同则不得奖.那么顾客摸奖一次,得奖的概率是 .
14.如图所示,小李和小陈做转陀螺游戏,他们同时分别转动一个陀螺,当两个陀螺都停下来时,与桌面相接触的边上的数字都是奇数的概率是 .
三、解答题(本大题共52分)
15.(本题8分)一袋中装有除颜色外都相同的红球和黄球共10个,其中红球6个.从袋中任意摸出一球,请问:
(1)“摸出的球是白球”是什么事件?它的概率是多少?
(2)“摸出的球是黄球”是什么事件?它的概率是多少?
(3)“摸出的球是红球或黄球”是什么事件?它的概率是多少?
16.(本题10分)妞妞和她的爸爸玩“锤子、剪刀、布”游戏.每次用一只手可以出锤子、剪刀、布三种手势之一,规则是锤子赢剪刀、剪刀赢布、布赢锤子,若两人出相同手势,则算打平.
(1)你帮妞妞算算爸爸出“锤子”手势的概率是多少?
(2)妞妞决定这次出“布”手势,妞妞赢的概率有多大?
(3)妞妞和爸爸出相同手势的概率是多少?
17.(本题10分)桌面上放有张卡片,正面分别标有数字,,,.这些卡片除数字外完全相同,把这些卡片反面朝上洗匀后放在桌面上,甲从中任意抽出一张,记下卡片上的数字后仍反面朝上放回洗匀,乙也从中任意抽出一张,记下卡片上的数字,然后将这两数相加.
(1)请用列表或画树形图的方法求两数之和为的概率.
(2)若甲与乙按上述方式做游戏,当两数之和为时,甲胜;反之则乙胜.若甲胜一次得分,那么乙胜一次得多少分,这个游戏对双方公平?
18.(本题12分)“六一”儿童节,小明与小亮受邀到科技馆担任义务讲解员,他们俩各自独立从A区(时代辉煌)、B区(科学启迪)、C区(智慧之光)、D区(儿童世界)这四个主题展区中随机选择一个为参观者服务.
(1)请用列表法或画树状图法说明当天小明与小亮出现在各主题展区担任义务讲解员的所有可能情况.(用字母表示)
(2)求小明与小亮只单独出现在B区(科学启迪)、C区(智慧之光)、D区(儿童世界)三个主题展区中担任义务讲解员的概率.
19、(本题12分)七巧板是我国流传已久的一种智力玩具,小鹏在玩七巧板时用它画成了3副图案并将它们贴在3张完全相同的不透明卡片上,如图.小鹏将这3张卡片背面朝上洗匀后放在桌子上,从中随机抽取一张,放回后洗匀,再随机抽取一张卡片.请你用列表法或画树状图(树形图)法,帮助小鹏求出两张卡片上的图案都是小动物的概率.(卡片名称可用字母表示)
四、附加题(本题为综合题,共20分)
20、在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只, 某学习小组做摸球实验, 将球搅匀后从中随机摸出一个球记下颜色, 再把它放回袋中, 不断重复. 下表是活动进行中的一组统计数据:
摸球的次数 100 150 200 500 800 1000
摸到白球的次数 58 96 116 295 484 601
摸到白球的频率 0.58 0.64 0.58 0.59 0.605 0.601
⑴ 请估计:当很大时, 摸到白球的频率将会接近 ;
⑵ 假如你去摸一次, 你摸到白球的概率是 , 摸到黑球的概率是 ;
⑶ 试估算口袋中黑、白两种颜色的球各有多少只
⑷ 解决了上面的问题, 小明同学猛然顿悟, 过去一个悬而未决的问题有办法了. 这个问题是: 在一个不透明的口袋里装有若干个白球, 在不允许将球倒出来数的情况下, 如何估计白球的个数(可以借助其他工具及用品) 请你应用统计与概率的思想和方法解决这个问题,写出解决这个问题的主要步骤及估算方法.
参考答案
1.D
2.C
3.B
4.A
5.D
6.B
7.D
8.B
9.明天
10.75
11.16
12.
13.
14.
15(1)“摸出的球是白球”是不可能事件,它的概率为;(2)“摸出的球是黄球”是不确定事件,它的概率为;(3)“摸出的球是红球或黄球”是必然事件,它的概率为.
16(1);(2);(3)
17(1)由列表(略)可得:(数字之和为) HYPERLINK "http://www./Index.html" EMBED Equation.DSMT4;
(2)因为(甲胜),(乙胜),甲胜一次得分,要使这个游戏对双方公平,乙胜一次的得分应为:分
18(1)(1)当天小明与小亮出现在各主题展区担任义务讲解员的所有可能情况画树形图如下:
(2)小明与小亮只单独出现在区(科学启迪)、区(智慧之光)、区(儿童世界)三个主题展区中担任义务讲解员的情况有
6种,故所求概率为
19解:列表得 或画树状图(树形图)得
A B C
A (A,A) (A,B) (A,C)
B (B,A) (B,B) (B,C)
C (C,A) (C,B) (C,C)
由表格(或画树状图/树形图)可知,共有9种等可能性结果,其中两张卡片上的图案都是小动物的结果有4种.
∴P(两张卡片上的图案都是小动物)=.
四、20.(1)0.6;(2)0.6;0.4;(3)黑球8个,白球12个;
(4)①先从不透明的口袋里摸出个白球,都涂上颜色(如黑色),然后放回口袋里,搅拌均匀;②将搅匀后的球从中随机摸出一个球记下颜色, 再把它放回袋中, 不断大量重复次,记录摸出黑球频数为;③根据用频数估计概率的方法可得出白球数为.
第13题图
4
5
6
7
8
9
4
5
6
1
2
3
第14题图
狐狸
A
兔子
C
小屋
B
A
A
B
C
D
B
A
B
C
D
C
A
B
C
D
D
A
B
C
D
第22题答案图
小明
小亮
第
二
张
第
一
张
