2020-2021学年北京课改版八下数学14.6一次函数的性质 同步练习(Word版 附答案)
文档属性
| 名称 | 2020-2021学年北京课改版八下数学14.6一次函数的性质 同步练习(Word版 附答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 75.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 00:00:00 | ||
图片预览


文档简介
北京课改版八下数学
14.6
一次函数的性质
一、选择题
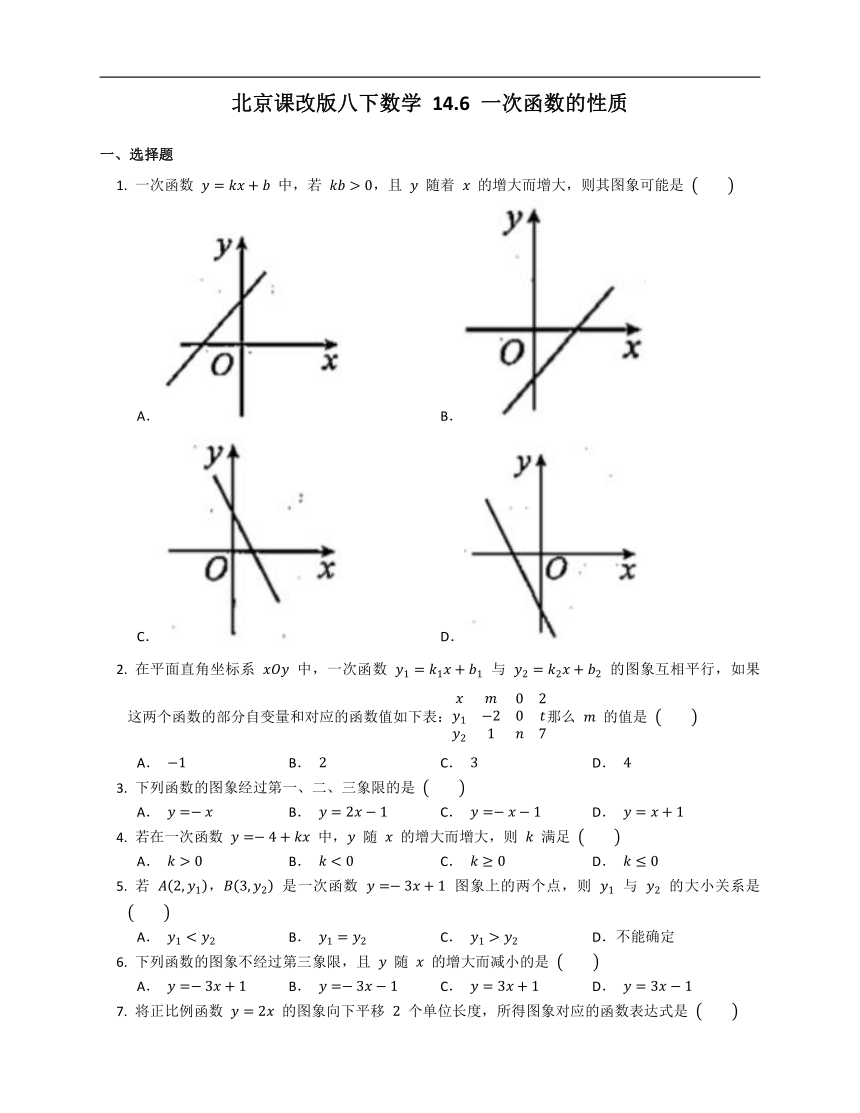
一次函数
中,若
,且
随着
的增大而增大,则其图象可能是
A.
B.
C.
D.
在平面直角坐标系
中,一次函数
与
的图象互相平行,如果这两个函数的部分自变量和对应的函数值如下表:那么
的值是
A.
B.
C.
D.
下列函数的图象经过第一、二、三象限的是
A.
B.
C.
D.
若在一次函数
中,
随
的增大而增大,则
满足
A.
B.
C.
D.
若
,
是一次函数
图象上的两个点,则
与
的大小关系是
A.
B.
C.
D.不能确定
下列函数的图象不经过第三象限,且
随
的增大而减小的是
A.
B.
C.
D.
将正比例函数
的图象向下平移
个单位长度,所得图象对应的函数表达式是
A.
B.
C.
D.
如图,在点
,,,
中,一次函数
的图象不可能经过的点是
A.
B.
C.
D.
如图,在平面直角坐标系
中,,
为一次函数图象上的两点,若点
的坐标为
,点
的坐标为
,则下列结论正确的是
A.
B.
C.
D.
二、填空题
若关于
的一次函数
中,
随
的增大而减小,则
的取值范围是
.
如果在函数
中,
随
的增大而增大,那么这个函数的图象不经过第
象限.
三、解答题
已知一次函数
.试回答:
(1)
为何值时,函数图象过原点?
(2)
若
随
的增大而增大,求
的取值范围.
已知一次函数
.
(1)
若其图象与一次函数
的图象平行,求
的值;
(2)
若函数
随
的增大而减小,并且函数的图象经过第二、三、四象限,求
的取值范围.
在平面直角坐标系
中,
是直线
上的一点,点
向右平移
个单位长度得到点
.
(1)
求点
,
的坐标;
(2)
若直线
与线段
有公共点,结合函数的图象,求
的取值范围.
若两个一次函数
,,则称函数
为这两个函数的“和谐函数”.
(1)
求一次函数
与
的“和谐函数”的表达式,若此“和谐函数”的图象与
轴相交于点
,与
轴相交于点
,求
的面积;
(2)
若一次函数
,
的“和谐函数”为
,则
,
;
(3)
已知一次函数
与
的“和谐函数”的图象经过第一、二、四象限,则常数
,
满足的条件为
.
已知一次函数
,当
时,,求此一次函数的表达式.
答案
一、选择题
1.
【答案】A
2.
【答案】A
【解析】
一次函数
与
的图象互相平行,
,
由表格中的对应数据可得:
解得
【知识点】一次函数图象的平行问题
3.
【答案】D
4.
【答案】A
5.
【答案】C
6.
【答案】A
7.
【答案】C
8.
【答案】A
9.
【答案】B
二、填空题
10.
【答案】
11.
【答案】四
三、解答题
12.
【答案】
(1)
.
(2)
.
13.
【答案】
(1)
(2)
14.
【答案】
(1)
因为
是直线
上的一点,
所以
,
所以点
的坐标为
,
所以点
向右平移
个单位长度得到点
的坐标为
.
(2)
当直线
过点
时,
得
,解得
.
直线
过点
时,
得
,解得
.
如图,
若直线
与线段
有公共点,则
的取值范围是
或
.
15.
【答案】
(1)
由题意得此“和谐函数”的表达式是
,即
.
令
,则
.
当
时,,解得
,
则
.
(2)
;
(3)
,
16.
【答案】当
时,一次函数
随
的增大而增大,即
时,,
时,,
代入得:解得:此时一次函数解析式为
;
当
时,一次函数
随
的增大而减小,即
时,,
时,,
代入得:解得:此时一次函数解析式为
,
综上,一次函数的表达式为
或
.
【知识点】一次函数的解析式
14.6
一次函数的性质
一、选择题
一次函数
中,若
,且
随着
的增大而增大,则其图象可能是
A.
B.
C.
D.
在平面直角坐标系
中,一次函数
与
的图象互相平行,如果这两个函数的部分自变量和对应的函数值如下表:那么
的值是
A.
B.
C.
D.
下列函数的图象经过第一、二、三象限的是
A.
B.
C.
D.
若在一次函数
中,
随
的增大而增大,则
满足
A.
B.
C.
D.
若
,
是一次函数
图象上的两个点,则
与
的大小关系是
A.
B.
C.
D.不能确定
下列函数的图象不经过第三象限,且
随
的增大而减小的是
A.
B.
C.
D.
将正比例函数
的图象向下平移
个单位长度,所得图象对应的函数表达式是
A.
B.
C.
D.
如图,在点
,,,
中,一次函数
的图象不可能经过的点是
A.
B.
C.
D.
如图,在平面直角坐标系
中,,
为一次函数图象上的两点,若点
的坐标为
,点
的坐标为
,则下列结论正确的是
A.
B.
C.
D.
二、填空题
若关于
的一次函数
中,
随
的增大而减小,则
的取值范围是
.
如果在函数
中,
随
的增大而增大,那么这个函数的图象不经过第
象限.
三、解答题
已知一次函数
.试回答:
(1)
为何值时,函数图象过原点?
(2)
若
随
的增大而增大,求
的取值范围.
已知一次函数
.
(1)
若其图象与一次函数
的图象平行,求
的值;
(2)
若函数
随
的增大而减小,并且函数的图象经过第二、三、四象限,求
的取值范围.
在平面直角坐标系
中,
是直线
上的一点,点
向右平移
个单位长度得到点
.
(1)
求点
,
的坐标;
(2)
若直线
与线段
有公共点,结合函数的图象,求
的取值范围.
若两个一次函数
,,则称函数
为这两个函数的“和谐函数”.
(1)
求一次函数
与
的“和谐函数”的表达式,若此“和谐函数”的图象与
轴相交于点
,与
轴相交于点
,求
的面积;
(2)
若一次函数
,
的“和谐函数”为
,则
,
;
(3)
已知一次函数
与
的“和谐函数”的图象经过第一、二、四象限,则常数
,
满足的条件为
.
已知一次函数
,当
时,,求此一次函数的表达式.
答案
一、选择题
1.
【答案】A
2.
【答案】A
【解析】
一次函数
与
的图象互相平行,
,
由表格中的对应数据可得:
解得
【知识点】一次函数图象的平行问题
3.
【答案】D
4.
【答案】A
5.
【答案】C
6.
【答案】A
7.
【答案】C
8.
【答案】A
9.
【答案】B
二、填空题
10.
【答案】
11.
【答案】四
三、解答题
12.
【答案】
(1)
.
(2)
.
13.
【答案】
(1)
(2)
14.
【答案】
(1)
因为
是直线
上的一点,
所以
,
所以点
的坐标为
,
所以点
向右平移
个单位长度得到点
的坐标为
.
(2)
当直线
过点
时,
得
,解得
.
直线
过点
时,
得
,解得
.
如图,
若直线
与线段
有公共点,则
的取值范围是
或
.
15.
【答案】
(1)
由题意得此“和谐函数”的表达式是
,即
.
令
,则
.
当
时,,解得
,
则
.
(2)
;
(3)
,
16.
【答案】当
时,一次函数
随
的增大而增大,即
时,,
时,,
代入得:解得:此时一次函数解析式为
;
当
时,一次函数
随
的增大而减小,即
时,,
时,,
代入得:解得:此时一次函数解析式为
,
综上,一次函数的表达式为
或
.
【知识点】一次函数的解析式
同课章节目录
