2021年河北中考数学一轮基础知识复习:勾股定理(word版含答案)
文档属性
| 名称 | 2021年河北中考数学一轮基础知识复习:勾股定理(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 942.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 17:09:07 | ||
图片预览




文档简介
2021年河北中考数学一轮基础知识复习:勾股定理
一、单选题
1.不能确定两个三角形全等的条件是(
)
A.三边对应相等
B.两边及其夹角相等
C.两角和任一边对应相等
D.三个角对应相等
2.矩形ABCD中,对角线AC、BD交于点O,如果AB=4,∠AOB=60°,那么AC的长等于(
)
A.16
B.8
C.16
D.8
3.如图,为了测量池塘的宽度,在池塘周围的平地上选择了、、三点,且、、、四点在同一条直线上,,已测得,,,,则池塘的宽度(
)
A.
B.
C.
D.
4.2020年10月1日至4日,全国共接待国内游客4.25亿人次,实现旅游收入3120.2亿元,其中与4.25最接近的数字是
A.
B.
C.
D.
5.下列各组数中,属于勾股数的是( )
A.2.5,6,6.5
B.5,7,10
C.,,,
D.6,8,10
6.如图,在中,,,,是边上一动点,连接,则的长度不可能是(
)
A.4
B.4.5
C.5
D.7
7.如图,半径为5的⊙P与y轴相交于M(0,-4),N(0,-10)两点,则圆心P的坐标为( )
A.
B.
C.
D.
8.下列各组数不是勾股数的是( )
A.5,12,13
B.6,8,10
C.32,42,52
D.3,4,5
9.如图,长方体的底面边长分别为2cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈达到点B,那么所用细线最短需要(
)
A.11cm
B.2cm
C.(8+2)cm
D.(7+3)cm
10.边长为5cm的菱形,一条对角线长是6cm,则另一条对角线的长是(
)cm.
A.3
B.4
C.6
D.8
11.如图,在中,,,,由绕点顺时针旋转得到,其中点与点、点与点是对应点,连接,且点、、在同一条直线上,则的长为(
)
A.3
B.
C.4
D.
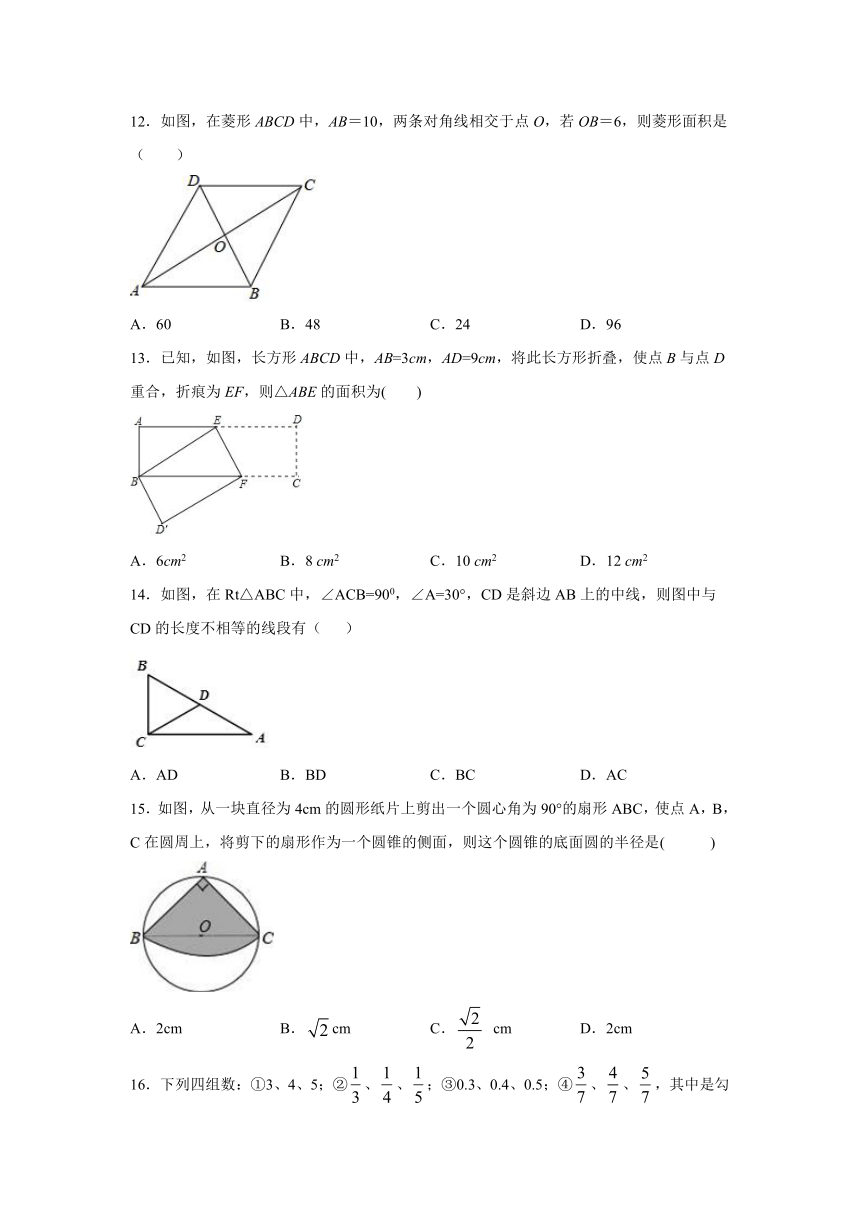
12.如图,在菱形ABCD中,AB=10,两条对角线相交于点O,若OB=6,则菱形面积是( )
A.60
B.48
C.24
D.96
13.已知,如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A.6cm2
B.8
cm2
C.10
cm2
D.12
cm2
14.如图,在Rt△ABC中,∠ACB=900,∠A=30°,CD是斜边AB上的中线,则图中与CD的长度不相等的线段有(
)
A.AD
B.BD
C.BC
D.AC
15.如图,从一块直径为4cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是(
)
A.2cm
B.cm
C.
cm
D.2cm
16.下列四组数:①3、4、5;②、、;③0.3、0.4、0.5;④、、,其中是勾股数的有
( )
A.4组
B.3组
C.2组
D.1组
17.如图,已知△ABC是腰长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2018个等腰直角三角形的斜边长是( )
A.21008
B.21009
C.22016
D.22018
18.如图,在平面直角坐标系中,的斜边在轴上,坐标原点是的中点,交轴于点,,的面积是1.若直角顶点在反比例函数的图象上,则的值是(
)
A.
B.3
C.
D.2
19.在ABC中,∠ACB=45°,
D为AC上一点,,连接BD,将ABD沿BD翻折至EBD,点A的对应点E点恰好落在边BC上,延长BC至点F,连接DF,若CF=2,,则DF长为(
)
A.
B.
C.
D.
20.如图,在等腰中,点为的中点,且.若,则的长为(
)
A.
B.
C.
D.
二、填空题
21.定义:对于实数,符号表示不大于的最大整数.例如:,,.如果,则满足条件的所有正整数的值是______.
22.纸质饮料盒是一个长方体,长6cm,宽4cm,高12cm,将一根长20cm的吸管从纸盒一角的小孔插入,为了能吸到纸盒内每一个角落,吸管露在盒外的长度最短为_____cm.
23.如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F若平行四边形CDEF的周长是25cm,AC的长为5cm,则的长是________.
24.如图,已知正方形
的边长为
,点
、
分别在边
、
上,且
,
、
交于点
.下列结论:,,,
中,正确的有________________.
25.如图所示,等边△ABC的边长为4,点D是BC边上一动点,且CE=BD,连接AD,BE,AD与BE相交于点P,连接PC.则线段PC的最小值等于_____.
三、解答题
26.先观察图形(如图所示),然后回答问题:
(1)设每个小方格的边长是1,则正方形的面积是______,正方形的面积是______,正方形的面积是______.
(2)正方形,正方形,正方形的面积之间有何关系?你能发现、、的关系吗?
27.把两个含有45°角的直角三角板ACB和DEC如图放置,点A,C,E在同一直线上,点D在BC上,连接BE,AD,AD的延长线交BE于点F.
(1)求证:△ADC≌△BEC;
(2)猜想AD与EB是否垂直?并说明理由.
28.如图所示,太阳光线AB和A′B′是平行的,甲、乙两人垂直站在地面上,在阳光照射下的影子一样长,那么甲、乙一样高吗?说明理由.
29.将两个完全相同的三角形纸片和重合放置,其中.
(1)操作发现:如图2,固定使绕点旋转,设的面积为的面积为当点恰好落在边上时,则与的数量关系是
;
(2)猜想论证:当绕点旋转到如图3所示的位置时,小明猜想中与的数量关系为相等,并尝试分别作出了和中边上的高请你证明小明的猜想,即证明:.
(3)拓展探究:已知,点是角平分线上的一点,交于点(如图4).若射线上存在点,使,请直接写出相应的的长.
参考答案
1--10DDCBD
DCCBD
11--20ADADC
DBADA
21.和.
22.6
23.13cm
24.①③④
25.
26.解:(1)根据题意,可得:
正方形的面积=,
正方形的面积=,
正方形的面积=;
故答案为:1,1,2.
(2)由(1)知,,
∴正方形的面积+正方形的面积=正方形的面积;
∵正方形的面积=,正方形的面积=,正方形的面积=,
∴.
27.详解:(1)∵△ABC和△ECD都是等腰直角三角形,∴∠ECD=∠BCA=90°,CE=CD,BC=AC,在△DCA和△ECB中,∵,∴△ADC≌△BEC(SAS);
(2)∵△ADC≌△BEC,∴AD=BE,∠BEC=∠ADC,又∠ADC+∠DAC=90°,∴∠BEC+∠DAC=90°,∴∠AFE=90°,即AD⊥BE.
28.解:一样高.理由如下:
如图,分别过点A,A′作AC⊥BB′,交直线BB′于点C,A′C′⊥BB′,交BB′于点C′,
则∠ACB=∠A′C′B′=90°,BC=B′C′.
又∵AB∥A′B′,
∴∠ABC=∠A′B′C′,
在△ABC和△A′B′C′中,
∵∠ACB=∠A′C′B′,BC=B′C′,∠ABC=∠A′B′C′,
∴△ABC≌△A′B′C′(ASA),
∴AC=A′C′,
即甲、乙两人一样高.
29.解:(1)∵△DEC绕点C旋转,点D恰好落在AB边上,∴AC=CD,
∵∠BAC=90°?∠B=90°?30°=60°,∴△ACD是等边三角形,
∵∠B=30°,∠C=90°,∴CD=AC=AB,∴BD=AD=AC,
根据等边三角形的性质,△ACD的边AC、AD上的高相等,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),即;
如图3.是由绕点旋转得到,
.
.
在和中.
的面积和的面积相等(等底等高的三角形的面积相等)即
(3)如图4,过点D作//BE,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵D//BE,DE//B,
∴四边形BED是平行四边形,∠ABD=∠BDE,
∴∠DBC=∠BDE,
∴BE=DE,
∴四边形BED是菱形,
∴BE=D,且BE、D上的高相等,
此时;
过点D作D⊥BD,
∵∠ABC=60°,D//BE,
∴∠D=∠ABC=60°,
∵B=D,∠BD=∠ABC=30°,∠DB=90°,
∴∠D=∠ABC=60°,
∴△D是等边三角形,
∴D=D,
∵BD=CD,∠ABC=60°,点D是角平分线上一点,
∴∠DBC=∠DCB=×60°=30°,
∴∠CD=180°?∠BCD=180°?30°=150°,∠CD=360°?150°?60°=150°,
∴∠CD=∠CD
∵在△CD和△CD中,D=D,∠CD=∠CD,CD=CD,
∴△CD≌△CD
(SAS),∴点也是所求的点,
又∵BE=4=B=D,△D是等边三角形,
∴B=4=,
∴B=8,
综上所述:当BF=4或8时,.
一、单选题
1.不能确定两个三角形全等的条件是(
)
A.三边对应相等
B.两边及其夹角相等
C.两角和任一边对应相等
D.三个角对应相等
2.矩形ABCD中,对角线AC、BD交于点O,如果AB=4,∠AOB=60°,那么AC的长等于(
)
A.16
B.8
C.16
D.8
3.如图,为了测量池塘的宽度,在池塘周围的平地上选择了、、三点,且、、、四点在同一条直线上,,已测得,,,,则池塘的宽度(
)
A.
B.
C.
D.
4.2020年10月1日至4日,全国共接待国内游客4.25亿人次,实现旅游收入3120.2亿元,其中与4.25最接近的数字是
A.
B.
C.
D.
5.下列各组数中,属于勾股数的是( )
A.2.5,6,6.5
B.5,7,10
C.,,,
D.6,8,10
6.如图,在中,,,,是边上一动点,连接,则的长度不可能是(
)
A.4
B.4.5
C.5
D.7
7.如图,半径为5的⊙P与y轴相交于M(0,-4),N(0,-10)两点,则圆心P的坐标为( )
A.
B.
C.
D.
8.下列各组数不是勾股数的是( )
A.5,12,13
B.6,8,10
C.32,42,52
D.3,4,5
9.如图,长方体的底面边长分别为2cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈达到点B,那么所用细线最短需要(
)
A.11cm
B.2cm
C.(8+2)cm
D.(7+3)cm
10.边长为5cm的菱形,一条对角线长是6cm,则另一条对角线的长是(
)cm.
A.3
B.4
C.6
D.8
11.如图,在中,,,,由绕点顺时针旋转得到,其中点与点、点与点是对应点,连接,且点、、在同一条直线上,则的长为(
)
A.3
B.
C.4
D.
12.如图,在菱形ABCD中,AB=10,两条对角线相交于点O,若OB=6,则菱形面积是( )
A.60
B.48
C.24
D.96
13.已知,如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A.6cm2
B.8
cm2
C.10
cm2
D.12
cm2
14.如图,在Rt△ABC中,∠ACB=900,∠A=30°,CD是斜边AB上的中线,则图中与CD的长度不相等的线段有(
)
A.AD
B.BD
C.BC
D.AC
15.如图,从一块直径为4cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是(
)
A.2cm
B.cm
C.
cm
D.2cm
16.下列四组数:①3、4、5;②、、;③0.3、0.4、0.5;④、、,其中是勾股数的有
( )
A.4组
B.3组
C.2组
D.1组
17.如图,已知△ABC是腰长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2018个等腰直角三角形的斜边长是( )
A.21008
B.21009
C.22016
D.22018
18.如图,在平面直角坐标系中,的斜边在轴上,坐标原点是的中点,交轴于点,,的面积是1.若直角顶点在反比例函数的图象上,则的值是(
)
A.
B.3
C.
D.2
19.在ABC中,∠ACB=45°,
D为AC上一点,,连接BD,将ABD沿BD翻折至EBD,点A的对应点E点恰好落在边BC上,延长BC至点F,连接DF,若CF=2,,则DF长为(
)
A.
B.
C.
D.
20.如图,在等腰中,点为的中点,且.若,则的长为(
)
A.
B.
C.
D.
二、填空题
21.定义:对于实数,符号表示不大于的最大整数.例如:,,.如果,则满足条件的所有正整数的值是______.
22.纸质饮料盒是一个长方体,长6cm,宽4cm,高12cm,将一根长20cm的吸管从纸盒一角的小孔插入,为了能吸到纸盒内每一个角落,吸管露在盒外的长度最短为_____cm.
23.如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F若平行四边形CDEF的周长是25cm,AC的长为5cm,则的长是________.
24.如图,已知正方形
的边长为
,点
、
分别在边
、
上,且
,
、
交于点
.下列结论:,,,
中,正确的有________________.
25.如图所示,等边△ABC的边长为4,点D是BC边上一动点,且CE=BD,连接AD,BE,AD与BE相交于点P,连接PC.则线段PC的最小值等于_____.
三、解答题
26.先观察图形(如图所示),然后回答问题:
(1)设每个小方格的边长是1,则正方形的面积是______,正方形的面积是______,正方形的面积是______.
(2)正方形,正方形,正方形的面积之间有何关系?你能发现、、的关系吗?
27.把两个含有45°角的直角三角板ACB和DEC如图放置,点A,C,E在同一直线上,点D在BC上,连接BE,AD,AD的延长线交BE于点F.
(1)求证:△ADC≌△BEC;
(2)猜想AD与EB是否垂直?并说明理由.
28.如图所示,太阳光线AB和A′B′是平行的,甲、乙两人垂直站在地面上,在阳光照射下的影子一样长,那么甲、乙一样高吗?说明理由.
29.将两个完全相同的三角形纸片和重合放置,其中.
(1)操作发现:如图2,固定使绕点旋转,设的面积为的面积为当点恰好落在边上时,则与的数量关系是
;
(2)猜想论证:当绕点旋转到如图3所示的位置时,小明猜想中与的数量关系为相等,并尝试分别作出了和中边上的高请你证明小明的猜想,即证明:.
(3)拓展探究:已知,点是角平分线上的一点,交于点(如图4).若射线上存在点,使,请直接写出相应的的长.
参考答案
1--10DDCBD
DCCBD
11--20ADADC
DBADA
21.和.
22.6
23.13cm
24.①③④
25.
26.解:(1)根据题意,可得:
正方形的面积=,
正方形的面积=,
正方形的面积=;
故答案为:1,1,2.
(2)由(1)知,,
∴正方形的面积+正方形的面积=正方形的面积;
∵正方形的面积=,正方形的面积=,正方形的面积=,
∴.
27.详解:(1)∵△ABC和△ECD都是等腰直角三角形,∴∠ECD=∠BCA=90°,CE=CD,BC=AC,在△DCA和△ECB中,∵,∴△ADC≌△BEC(SAS);
(2)∵△ADC≌△BEC,∴AD=BE,∠BEC=∠ADC,又∠ADC+∠DAC=90°,∴∠BEC+∠DAC=90°,∴∠AFE=90°,即AD⊥BE.
28.解:一样高.理由如下:
如图,分别过点A,A′作AC⊥BB′,交直线BB′于点C,A′C′⊥BB′,交BB′于点C′,
则∠ACB=∠A′C′B′=90°,BC=B′C′.
又∵AB∥A′B′,
∴∠ABC=∠A′B′C′,
在△ABC和△A′B′C′中,
∵∠ACB=∠A′C′B′,BC=B′C′,∠ABC=∠A′B′C′,
∴△ABC≌△A′B′C′(ASA),
∴AC=A′C′,
即甲、乙两人一样高.
29.解:(1)∵△DEC绕点C旋转,点D恰好落在AB边上,∴AC=CD,
∵∠BAC=90°?∠B=90°?30°=60°,∴△ACD是等边三角形,
∵∠B=30°,∠C=90°,∴CD=AC=AB,∴BD=AD=AC,
根据等边三角形的性质,△ACD的边AC、AD上的高相等,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),即;
如图3.是由绕点旋转得到,
.
.
在和中.
的面积和的面积相等(等底等高的三角形的面积相等)即
(3)如图4,过点D作//BE,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵D//BE,DE//B,
∴四边形BED是平行四边形,∠ABD=∠BDE,
∴∠DBC=∠BDE,
∴BE=DE,
∴四边形BED是菱形,
∴BE=D,且BE、D上的高相等,
此时;
过点D作D⊥BD,
∵∠ABC=60°,D//BE,
∴∠D=∠ABC=60°,
∵B=D,∠BD=∠ABC=30°,∠DB=90°,
∴∠D=∠ABC=60°,
∴△D是等边三角形,
∴D=D,
∵BD=CD,∠ABC=60°,点D是角平分线上一点,
∴∠DBC=∠DCB=×60°=30°,
∴∠CD=180°?∠BCD=180°?30°=150°,∠CD=360°?150°?60°=150°,
∴∠CD=∠CD
∵在△CD和△CD中,D=D,∠CD=∠CD,CD=CD,
∴△CD≌△CD
(SAS),∴点也是所求的点,
又∵BE=4=B=D,△D是等边三角形,
∴B=4=,
∴B=8,
综上所述:当BF=4或8时,.
