2020-2021学年八年级数学人教版下册 17.1勾股定理提高卷A(Word版 含答案)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册 17.1勾股定理提高卷A(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 589.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 13:55:52 | ||
图片预览


文档简介
17.1勾股定理
提高卷A
一、单选题(40分)
1.已知中,,,的对边分别为、、,若,则(
).
A.
B.
C.
D.
2.下列各组数据中,是勾股数的是(
)
A.3,4,5
B.1,2,3
C.8,9,10
D.5,6,9
3.下列各组数是勾股数的是(
)
A.0.3,0.4,0.5
B.7,8,9
C.6,8,10
D.,,
4.下列四组数中,是勾股数的是(
)
A.
B.
C.
D.
5.如图,在中,,,.以为一条边向三角形外部作正方形,则正方形的面积是(
)
A.
B.
C.
D.
6.如图,在中,,,过点作,交于点,若,则的长度为(
)
A.
B.
C.
D.
7.如图,原来从A村到B村,需要沿路A→C→B()绕过两地间的一片湖,在A,B间建好桥后,就可直接从A村到B村.已知,,那么,建好桥后从A村到B村比原来减少的路程为(
)
A.2km
B.4km
C.10
km
D.14
km
8.《九章算术》是我国古代的数学名著,其中“勾股”章有一题,大意是说:已知矩形门的高比宽多尺,门的对角线长尺,那么门的高和宽各是多少?如果设门的宽为尺,根据题意可列方程(
)
A.
B.
C.
D.
9.如图,长方形的长为3,宽为2,对角线为,且,则下列各数中与点表示的数最接近的是(
)
A.-3.5
B.-3.6
C.-3.7
D.-3.8
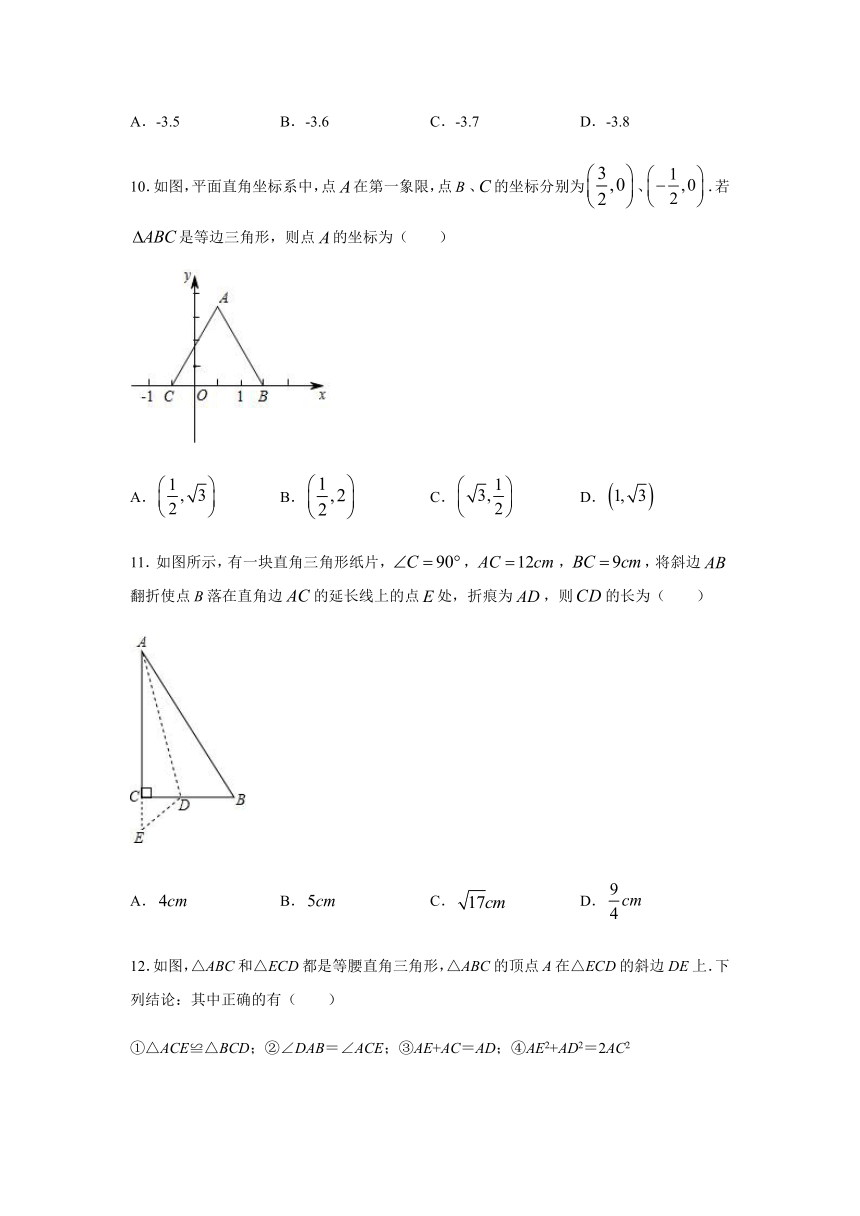
10.如图,平面直角坐标系中,点在第一象限,点、的坐标分别为、.若是等边三角形,则点的坐标为(
)
A.
B.
C.
D.
11.如图所示,有一块直角三角形纸片,,,,将斜边翻折使点落在直角边的延长线上的点处,折痕为,则的长为(
)
A.
B.
C.
D.
12.如图,△ABC和△ECD都是等腰直角三角形,△ABC的顶点A在△ECD的斜边DE上.下列结论:其中正确的有( )
①△ACE≌△BCD;②∠DAB=∠ACE;③AE+AC=AD;④AE2+AD2=2AC2
A.1个
B.2个
C.3个
D.4个
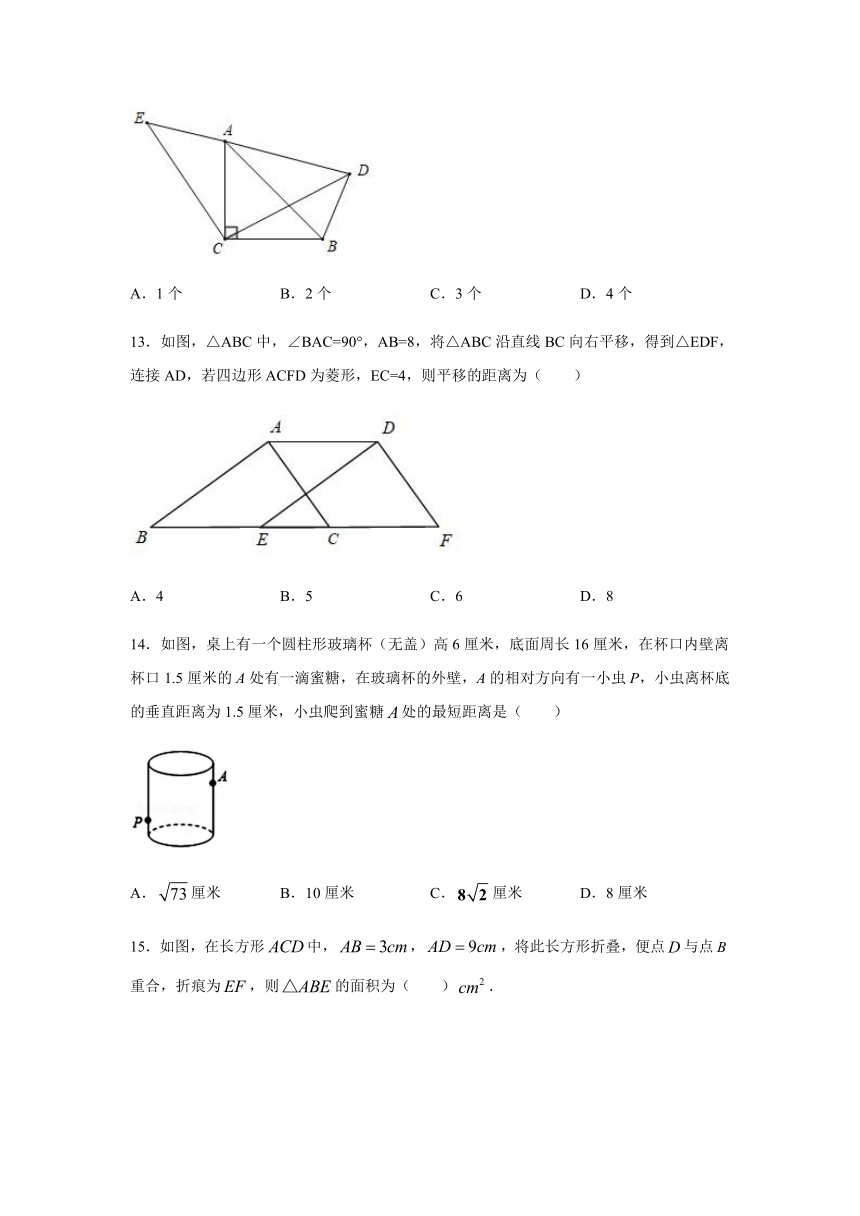
13.如图,△ABC中,∠BAC=90°,AB=8,将△ABC沿直线BC向右平移,得到△EDF,连接AD,若四边形ACFD为菱形,EC=4,则平移的距离为(
)
A.4
B.5
C.6
D.8
14.如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的A处有一滴蜜糖,在玻璃杯的外壁,A的相对方向有一小虫P,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖处的最短距离是(
)
A.厘米
B.10厘米
C.厘米
D.8厘米
15.如图,在长方形中,,,将此长方形折叠,便点与点重合,折痕为,则的面积为(
).
A.12
B.10
C.6
D.15
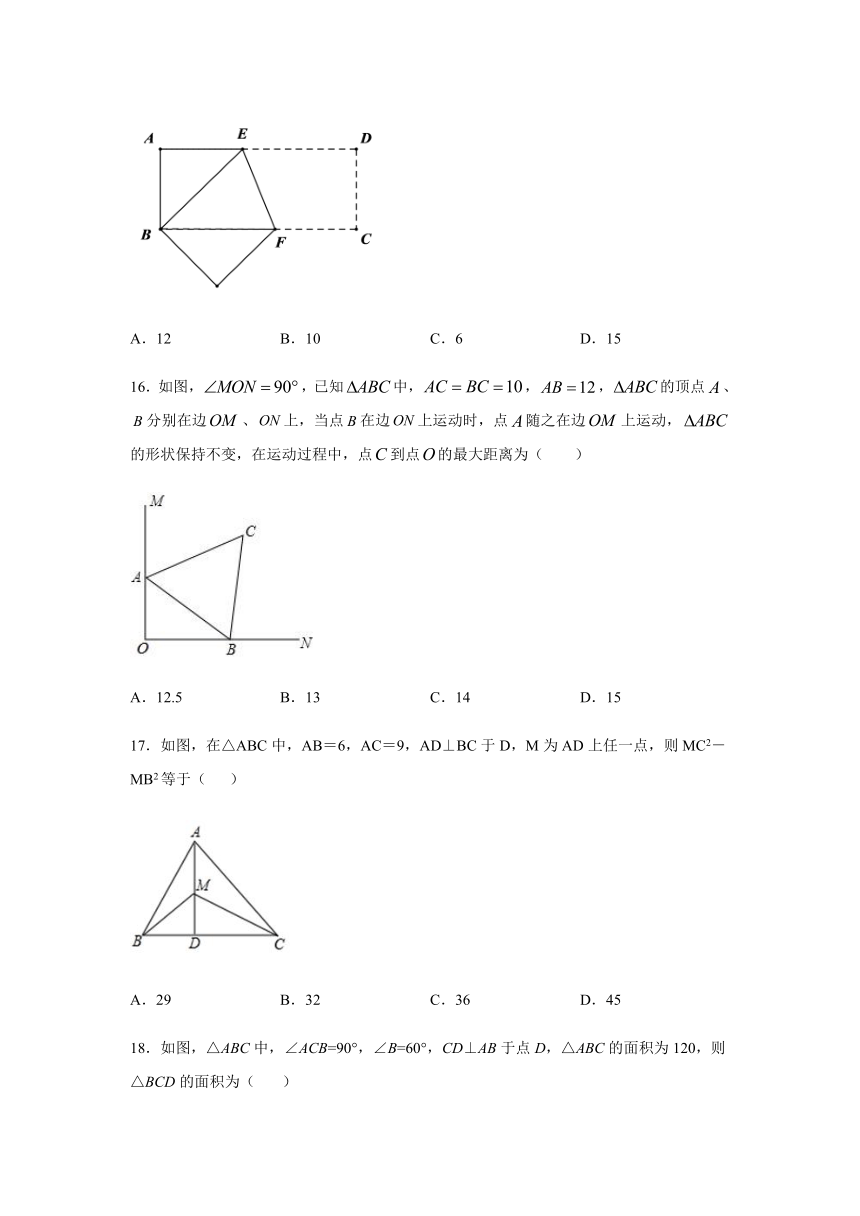
16.如图,,已知中,,,的顶点、分别在边、上,当点在边上运动时,点随之在边上运动,的形状保持不变,在运动过程中,点到点的最大距离为(
)
A.12.5
B.13
C.14
D.15
17.如图,在△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于(
)
A.29
B.32
C.36
D.45
18.如图,△ABC中,∠ACB=90°,∠B=60°,CD⊥AB于点D,△ABC的面积为120,则△BCD的面积为(???
)
A.20
B.24
C.30
D.40
19.如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=8,AB的垂直平分线DE交BC的延长线于点E,则DE的长为(
)
A.
B.
C.
D.
20.在△ABC中,∠BAC=90°,点D在边BC上,AD=AB
(
)
A.若AC=2AB,则∠C=30°
B.若AC=2AB,则3BD=2CD
C.若∠B=2∠C,则AC=2AB
D.若∠B=2∠C,则S△ABD=2△ACD
二、填空题(15分)
21.在Rt△ABC中,∠C=90°,若,则的长是
________
.
22.将一根长为的筷子置于底面直径为,高为的圆柱形水杯中,则筷子露在杯子外面的最短长度为_____.
23.在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E.使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,则AB=____cm.
24.如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成.设AB=x,若为直角三角形,则x=__.
25.如图,在△ABC中,∠ACB=90°,AC=BC=6cm,D是AB的中点,点E在AC上,过点D作DF⊥DE,交BC于点F.如果AE=2cm,则四边形CEDF的周长是_____cm.
三、解答题(65分)
26.中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展,现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°.AC=b,BC=a,AB=c,请你利用这个图形解决下列问题:
(1)试说明:a2+b2=c2;
(2)如果大正方形的面积是13,小正方形的面积是3,求(a+b)2的值.
27.在中,,,.如图1,若时,根据勾股定理有.
(1)如图2,当为锐角三角形时,类比勾股定理,判断与的大小关系,并证明;
(2)如图3,当为钝角三角形时,类比勾股定理,判断与的大小关系,并证明;
(3)如图4,一块四边形的试验田,已知,米,米,米,米,求这块试验田的面积.
28.如图,Rt△ABC中,∠ACB=90°,BC=AC=3,点D是CB延长线上的一个动点,线段AD绕点A逆时针旋转90°,得到线段AE,连结BE,与AC的延长线交于点M.
(1)若BD=1,△ADC中AD边上的高为h,求h的值;
(2)求证:M为BE的中点;
(3)当D点在CB延长线上运动时,探索的值是否变化?若不变,请求其值;若变化,请说明理由.
29.在锐角中,∠BAC=45°.
(1)如图1,BD⊥AC于D,在BD上取点E,使DE=CD,连结AE,F为AC的中点,连结EF并延长至点M,使FM=EF,连结CM、BM.
①求证:△AEF≌△CMF;
②若BC=2,求线段BM
的长.
如图2,P
是△ABC内的一点,
(即),AC=3,求PA+PB+PC
的最小值,并求此时∠APC的度数.
参考答案
1---10AACAD
BBABA
11--20ACCBC
CDCCB
21.17.
22.4
23.
24.或
25.6+2
26.解:(1)∵大正方形面积为c2,直角三角形面积为ab,小正方形面积为(b﹣a)2,
∴c2=4×ab+(a﹣b)2=2ab+a2﹣2ab+b2即c2=a2+b2;
(2)由图可知:
(b﹣a)2=3,4×ab=13﹣3=10,
∴2ab=10,
∴(a+b)2=(b﹣a)2+4ab=3+2×10=23.
27.解:(1)猜想:
,
证明:如图2,过点作于点,设,则,
在Rt中,有,
在Rt中,有
,
∴
,
解之:,
∵均为正数,∴
;
(2)猜想:
证明:如图3,过点作,交的延长线于点,设,则,
在Rt中,有,
在Rt中,有
,
∴,
解之:,
∵均为正数,∴
;
(3)如图4,连接.
在Rt中,有,
∴,
∵,∴
,
过点作于点E,
设,则EC=100-x,
在Rt中,有,即,
在Rt中,有,即
,
∴,
解之:,
在Rt中,有,
∴DE=(取正),
∴DE=,
∴,
=,
=(米2),
∴四边形ABCD的面积是米2.
28.解:(1)∵AC=BC=3,BD=1
∴CD=3+1=4,
在Rt△ACD中,
∵,
∴
(2)过E点作EF⊥AC于F,
∵AD⊥AE
,EF⊥AF,
∴∠DAE=∠AFE=90°,
∵∠DAC+∠EAF=90°,
∠EAF+∠AEF=90°,
∴∠DAC=∠AEF,
在△ACD和△EFA中,
∴△ACD≌△EFA(AAS)
∴EF=AC=3
,AF=CD,
∵AC=CB,
∴CB=EF,
在△BCM和△EFM中,
∴△BCM≌△EFM(AAS)
,
∴BM=EM,
∴M为BE的中点
(3)
由(2)知△BCM≌△EFM,
∴CM=FM,
∴CM=CF,
由(2)知△ACD≌△EFA,∴AF=CD,
∵AC=CB,
又∵CF=AF-AC,
∴CF=CD-CB=BD
,
∵CM=CF=BD,
∴=.
29.(1)①∵F为AC的中点,
∴AF=CF
在△AEF和△CMF中
∴△AEF≌△CMF
②由(1)得△AEF≌△CMF,
∴AE=CM,∠DAE=∠FCM,
∵BD⊥AC,∠BAC=45°,
∴AD=BD
在△AED和△BCD中
∴△AED≌△BCD,.
∴AE=BC,∠DAE=∠DBC,
∴BC=CM,∠FCM=∠DBC,
∵∠BCF+∠DBC=90°,
∴∠BCF+∠FCM=90°,
∴△BCM是等腰直角三角形,
由勾股定理得,
(2)将△APB
绕点A逆时针旋转
90°得到△AFE,连接FP、CE,
易知△AFP
是等腰直角三角形,
∴,∠EAC=135°,
作
EH⊥CA
交
CA
的延长线于
H.
在Rt△
EAH
中,
,
∵∠H=90°
,
∠EAH=45°,
∵=8,
∴EH=AH=2,
∴CH=5,
在
Rt△EHC
中,
∵PA+PB+PC=FP+EF+PC≥CE,
∴点C、P、F、E四点共线时,PA+PB+PC的最小值为CE,
此时,∠AFP+∠AFE=90°,∠BPC+∠APF=180°,
∵∠AFP=∠APF=45°,
∴∠AFE=∠BPC=135°,
∴∠APB=∠BPC=135°
∴∠APC=360°-135°-135°=90°
∴PA+PB+PC
的最小值为,此时∠APC=90°
提高卷A
一、单选题(40分)
1.已知中,,,的对边分别为、、,若,则(
).
A.
B.
C.
D.
2.下列各组数据中,是勾股数的是(
)
A.3,4,5
B.1,2,3
C.8,9,10
D.5,6,9
3.下列各组数是勾股数的是(
)
A.0.3,0.4,0.5
B.7,8,9
C.6,8,10
D.,,
4.下列四组数中,是勾股数的是(
)
A.
B.
C.
D.
5.如图,在中,,,.以为一条边向三角形外部作正方形,则正方形的面积是(
)
A.
B.
C.
D.
6.如图,在中,,,过点作,交于点,若,则的长度为(
)
A.
B.
C.
D.
7.如图,原来从A村到B村,需要沿路A→C→B()绕过两地间的一片湖,在A,B间建好桥后,就可直接从A村到B村.已知,,那么,建好桥后从A村到B村比原来减少的路程为(
)
A.2km
B.4km
C.10
km
D.14
km
8.《九章算术》是我国古代的数学名著,其中“勾股”章有一题,大意是说:已知矩形门的高比宽多尺,门的对角线长尺,那么门的高和宽各是多少?如果设门的宽为尺,根据题意可列方程(
)
A.
B.
C.
D.
9.如图,长方形的长为3,宽为2,对角线为,且,则下列各数中与点表示的数最接近的是(
)
A.-3.5
B.-3.6
C.-3.7
D.-3.8
10.如图,平面直角坐标系中,点在第一象限,点、的坐标分别为、.若是等边三角形,则点的坐标为(
)
A.
B.
C.
D.
11.如图所示,有一块直角三角形纸片,,,,将斜边翻折使点落在直角边的延长线上的点处,折痕为,则的长为(
)
A.
B.
C.
D.
12.如图,△ABC和△ECD都是等腰直角三角形,△ABC的顶点A在△ECD的斜边DE上.下列结论:其中正确的有( )
①△ACE≌△BCD;②∠DAB=∠ACE;③AE+AC=AD;④AE2+AD2=2AC2
A.1个
B.2个
C.3个
D.4个
13.如图,△ABC中,∠BAC=90°,AB=8,将△ABC沿直线BC向右平移,得到△EDF,连接AD,若四边形ACFD为菱形,EC=4,则平移的距离为(
)
A.4
B.5
C.6
D.8
14.如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的A处有一滴蜜糖,在玻璃杯的外壁,A的相对方向有一小虫P,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖处的最短距离是(
)
A.厘米
B.10厘米
C.厘米
D.8厘米
15.如图,在长方形中,,,将此长方形折叠,便点与点重合,折痕为,则的面积为(
).
A.12
B.10
C.6
D.15
16.如图,,已知中,,,的顶点、分别在边、上,当点在边上运动时,点随之在边上运动,的形状保持不变,在运动过程中,点到点的最大距离为(
)
A.12.5
B.13
C.14
D.15
17.如图,在△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于(
)
A.29
B.32
C.36
D.45
18.如图,△ABC中,∠ACB=90°,∠B=60°,CD⊥AB于点D,△ABC的面积为120,则△BCD的面积为(???
)
A.20
B.24
C.30
D.40
19.如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=8,AB的垂直平分线DE交BC的延长线于点E,则DE的长为(
)
A.
B.
C.
D.
20.在△ABC中,∠BAC=90°,点D在边BC上,AD=AB
(
)
A.若AC=2AB,则∠C=30°
B.若AC=2AB,则3BD=2CD
C.若∠B=2∠C,则AC=2AB
D.若∠B=2∠C,则S△ABD=2△ACD
二、填空题(15分)
21.在Rt△ABC中,∠C=90°,若,则的长是
________
.
22.将一根长为的筷子置于底面直径为,高为的圆柱形水杯中,则筷子露在杯子外面的最短长度为_____.
23.在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E.使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,则AB=____cm.
24.如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成.设AB=x,若为直角三角形,则x=__.
25.如图,在△ABC中,∠ACB=90°,AC=BC=6cm,D是AB的中点,点E在AC上,过点D作DF⊥DE,交BC于点F.如果AE=2cm,则四边形CEDF的周长是_____cm.
三、解答题(65分)
26.中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展,现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°.AC=b,BC=a,AB=c,请你利用这个图形解决下列问题:
(1)试说明:a2+b2=c2;
(2)如果大正方形的面积是13,小正方形的面积是3,求(a+b)2的值.
27.在中,,,.如图1,若时,根据勾股定理有.
(1)如图2,当为锐角三角形时,类比勾股定理,判断与的大小关系,并证明;
(2)如图3,当为钝角三角形时,类比勾股定理,判断与的大小关系,并证明;
(3)如图4,一块四边形的试验田,已知,米,米,米,米,求这块试验田的面积.
28.如图,Rt△ABC中,∠ACB=90°,BC=AC=3,点D是CB延长线上的一个动点,线段AD绕点A逆时针旋转90°,得到线段AE,连结BE,与AC的延长线交于点M.
(1)若BD=1,△ADC中AD边上的高为h,求h的值;
(2)求证:M为BE的中点;
(3)当D点在CB延长线上运动时,探索的值是否变化?若不变,请求其值;若变化,请说明理由.
29.在锐角中,∠BAC=45°.
(1)如图1,BD⊥AC于D,在BD上取点E,使DE=CD,连结AE,F为AC的中点,连结EF并延长至点M,使FM=EF,连结CM、BM.
①求证:△AEF≌△CMF;
②若BC=2,求线段BM
的长.
如图2,P
是△ABC内的一点,
(即),AC=3,求PA+PB+PC
的最小值,并求此时∠APC的度数.
参考答案
1---10AACAD
BBABA
11--20ACCBC
CDCCB
21.17.
22.4
23.
24.或
25.6+2
26.解:(1)∵大正方形面积为c2,直角三角形面积为ab,小正方形面积为(b﹣a)2,
∴c2=4×ab+(a﹣b)2=2ab+a2﹣2ab+b2即c2=a2+b2;
(2)由图可知:
(b﹣a)2=3,4×ab=13﹣3=10,
∴2ab=10,
∴(a+b)2=(b﹣a)2+4ab=3+2×10=23.
27.解:(1)猜想:
,
证明:如图2,过点作于点,设,则,
在Rt中,有,
在Rt中,有
,
∴
,
解之:,
∵均为正数,∴
;
(2)猜想:
证明:如图3,过点作,交的延长线于点,设,则,
在Rt中,有,
在Rt中,有
,
∴,
解之:,
∵均为正数,∴
;
(3)如图4,连接.
在Rt中,有,
∴,
∵,∴
,
过点作于点E,
设,则EC=100-x,
在Rt中,有,即,
在Rt中,有,即
,
∴,
解之:,
在Rt中,有,
∴DE=(取正),
∴DE=,
∴,
=,
=(米2),
∴四边形ABCD的面积是米2.
28.解:(1)∵AC=BC=3,BD=1
∴CD=3+1=4,
在Rt△ACD中,
∵,
∴
(2)过E点作EF⊥AC于F,
∵AD⊥AE
,EF⊥AF,
∴∠DAE=∠AFE=90°,
∵∠DAC+∠EAF=90°,
∠EAF+∠AEF=90°,
∴∠DAC=∠AEF,
在△ACD和△EFA中,
∴△ACD≌△EFA(AAS)
∴EF=AC=3
,AF=CD,
∵AC=CB,
∴CB=EF,
在△BCM和△EFM中,
∴△BCM≌△EFM(AAS)
,
∴BM=EM,
∴M为BE的中点
(3)
由(2)知△BCM≌△EFM,
∴CM=FM,
∴CM=CF,
由(2)知△ACD≌△EFA,∴AF=CD,
∵AC=CB,
又∵CF=AF-AC,
∴CF=CD-CB=BD
,
∵CM=CF=BD,
∴=.
29.(1)①∵F为AC的中点,
∴AF=CF
在△AEF和△CMF中
∴△AEF≌△CMF
②由(1)得△AEF≌△CMF,
∴AE=CM,∠DAE=∠FCM,
∵BD⊥AC,∠BAC=45°,
∴AD=BD
在△AED和△BCD中
∴△AED≌△BCD,.
∴AE=BC,∠DAE=∠DBC,
∴BC=CM,∠FCM=∠DBC,
∵∠BCF+∠DBC=90°,
∴∠BCF+∠FCM=90°,
∴△BCM是等腰直角三角形,
由勾股定理得,
(2)将△APB
绕点A逆时针旋转
90°得到△AFE,连接FP、CE,
易知△AFP
是等腰直角三角形,
∴,∠EAC=135°,
作
EH⊥CA
交
CA
的延长线于
H.
在Rt△
EAH
中,
,
∵∠H=90°
,
∠EAH=45°,
∵=8,
∴EH=AH=2,
∴CH=5,
在
Rt△EHC
中,
∵PA+PB+PC=FP+EF+PC≥CE,
∴点C、P、F、E四点共线时,PA+PB+PC的最小值为CE,
此时,∠AFP+∠AFE=90°,∠BPC+∠APF=180°,
∵∠AFP=∠APF=45°,
∴∠AFE=∠BPC=135°,
∴∠APB=∠BPC=135°
∴∠APC=360°-135°-135°=90°
∴PA+PB+PC
的最小值为,此时∠APC=90°
