人教版八年级下册16.1.1 《二次根式》 二次根式的概念课件(18张)
文档属性
| 名称 | 人教版八年级下册16.1.1 《二次根式》 二次根式的概念课件(18张) |  | |
| 格式 | ppt | ||
| 文件大小 | 203.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 16:15:22 | ||
图片预览




文档简介
第十六章 二次根式
16.1 二次根式
16.1.1 二次根式的概念
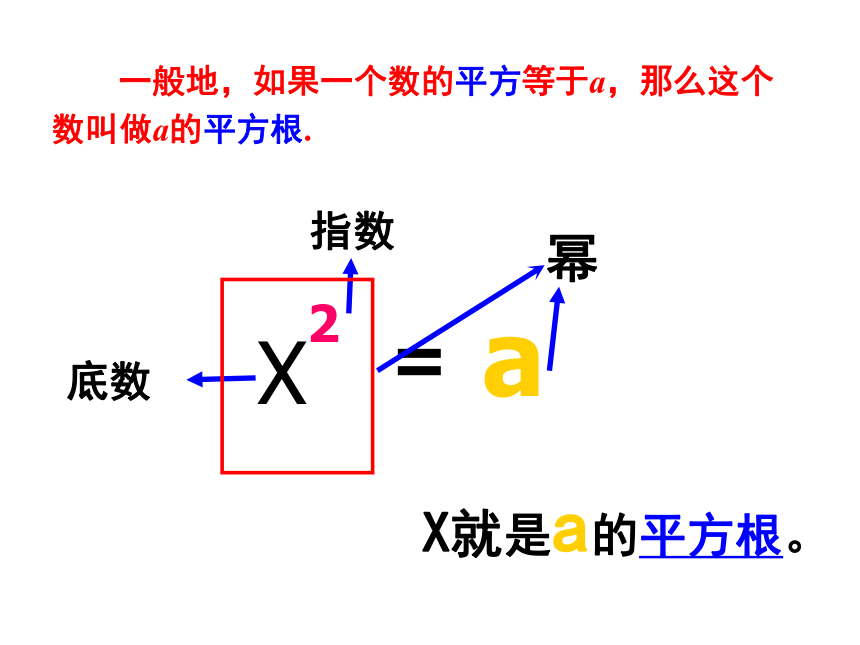
X就是a的平方根。
X2
底数
指数
幂
=
a
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根.
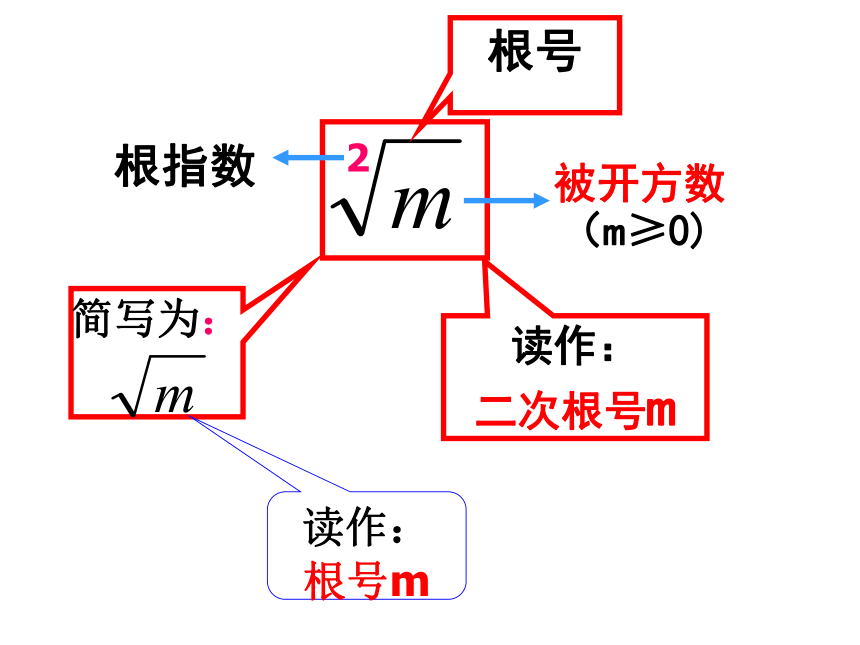
2
根指数
被开方数
读作:
二次根号m
简写为:
读作:
根号m
(m≥0)
根号
表示一些正数的算术平方根
1).4的平方根是_____;0的平方根是______.
2).5的平方根是_______;5的算术平方根是____.
0
议一议
(1)-1有算术平方根吗?
(2)0的算术平方根是多少?
(3)当 <0时, 有平方根吗?
(没有)
(0)
(没有)
问题1 这些式子分别表示什么意义?
问题2 这些式子有什么共同特征?
小结:
一个正数有两个平方根;
0的平方根为0;
在实数范围内,负数没有平方根;
因此,开方时被开方数只能为正数或0.
一般地,我们把形如 的式子叫做二次根式. “ ”称为二次根号.
两个必备特征
①外貌特征:含有“ ”
②内在特征:被开方数a ≥0
注意:a可以是数,也可以是式.
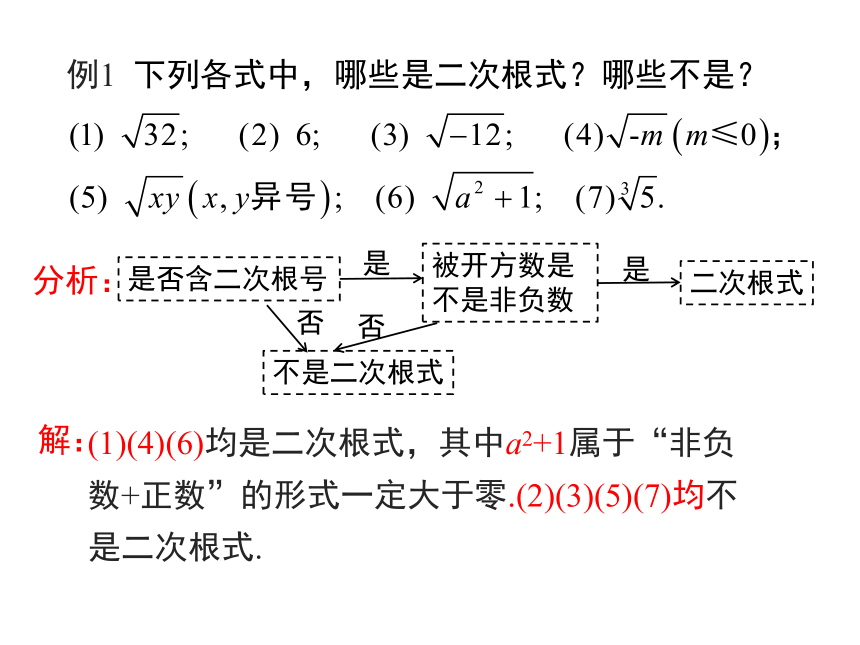
例1 下列各式中,哪些是二次根式?哪些不是?
解:
(1)(4)(6)均是二次根式,其中a2+1属于“非负数+正数”的形式一定大于零.(2)(3)(5)(7)均不是二次根式.
是否含二次根号
被开方数是不是非负数
二次根式
不是二次根式
是
是
否
否
分析:
例2 当x是怎样的实数时, 在实数范围内有
意义?
解:由x-2≥0,得
x≥2.
当x≥2时, 在实数范围内有意义.
解:由题意得x-1>0,
∴x>1.
解:∵被开方数需大于或等于零,
∴3+x≥0,∴x≥-3.
∵分母不能等于零,
∴x-1≠0,∴x≠1.
∴x≥-3 且x≠1.
要使二次根式在实数范围内有意义,即需满足被开方数≥0,列不等式求解即可.若式子为分式,应同时考虑分母不为零.
总结:
求二次根式中字母的取值范围的基本依据:
①被开方数不小于0;
②分母中有字母时,要保证分母不为0.
1.下列各式: .
一定是二次根式的有 ( )
A.3个 B.4个 C.5个 D.6个
B
2.(1)若式子 在实数范围内有意义,则x的取值
范围是_______;
(2)若式子 在实数范围内有意义,则x的
取值范围是___________.
x ≥1
x ≥0且x≠2
二次根式的实质是表示一个非负数(或式)的算术平方根.对于任意一个二次根式 ,我们知道:
(1)a为被开方数,为保证其有意义,可知a≥0;
(2) 表示一个数或式的算术平方根,可知 ≥0.
二次根式的被开方数非负
二次根式的值非负
二次根式的双重非负性
3 若 ,求a -b+c的值.
解:
由题意可知a-2=0,b-3=0,c-4=0,
解得a=2,b=3,c=4.
所以a-b+c=2-3+4=3.
总结:多个非负数的和为零,则可得每个非负数均为零.初中阶段学过的非负数主要有绝对值、偶次幂及二次根式.
4 已知y= ,求3x+2y的算术平方根.
解:由题意得
∴x=3,∴y=8,
∴3x+2y=25.
∵25的算术平方根为5,
∴3x+2y的算术平方根为5.
五、归纳总结
本节课主要学习了二次根式的定义及被开方数的取值范围.
(1)本节课你学习了哪些知识?
(2)利用本节课知识,你能解决什么问题?
利用本节课知识,解决了使二次根式在实数范围内有意义的被开方数的取值范围问题,此问题在计算中经常作为隐含条件给出,注意合理应用.
2.式子 有意义的条件是 ( )
A.x>2 B.x≥2 C.x<2 D.x≤2
3.当x=____时,二次根式 取最小值,其最小值
为______.
1. 下列式子中,不属于二次根式的是( )
C
A
-1
0
4.当a是怎样的实数时,下列各式在实数范围内有
意义?
5.(1)若二次根式 有意义,求m的取值范围.
解:由题意得m-2≥0且m2-4≠0,
解得m≥2且m≠-2,m≠2,
∴m>2.
(2)无论x取任何实数,代数式 都有意义,求m的取值范围.
解:由题意得x2+6x+m≥0,
即(x+3)2+m-9≥0.
∵(x+3)2≥0,
∴m-9≥0,即m≥9.
16.1 二次根式
16.1.1 二次根式的概念
X就是a的平方根。
X2
底数
指数
幂
=
a
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根.
2
根指数
被开方数
读作:
二次根号m
简写为:
读作:
根号m
(m≥0)
根号
表示一些正数的算术平方根
1).4的平方根是_____;0的平方根是______.
2).5的平方根是_______;5的算术平方根是____.
0
议一议
(1)-1有算术平方根吗?
(2)0的算术平方根是多少?
(3)当 <0时, 有平方根吗?
(没有)
(0)
(没有)
问题1 这些式子分别表示什么意义?
问题2 这些式子有什么共同特征?
小结:
一个正数有两个平方根;
0的平方根为0;
在实数范围内,负数没有平方根;
因此,开方时被开方数只能为正数或0.
一般地,我们把形如 的式子叫做二次根式. “ ”称为二次根号.
两个必备特征
①外貌特征:含有“ ”
②内在特征:被开方数a ≥0
注意:a可以是数,也可以是式.
例1 下列各式中,哪些是二次根式?哪些不是?
解:
(1)(4)(6)均是二次根式,其中a2+1属于“非负数+正数”的形式一定大于零.(2)(3)(5)(7)均不是二次根式.
是否含二次根号
被开方数是不是非负数
二次根式
不是二次根式
是
是
否
否
分析:
例2 当x是怎样的实数时, 在实数范围内有
意义?
解:由x-2≥0,得
x≥2.
当x≥2时, 在实数范围内有意义.
解:由题意得x-1>0,
∴x>1.
解:∵被开方数需大于或等于零,
∴3+x≥0,∴x≥-3.
∵分母不能等于零,
∴x-1≠0,∴x≠1.
∴x≥-3 且x≠1.
要使二次根式在实数范围内有意义,即需满足被开方数≥0,列不等式求解即可.若式子为分式,应同时考虑分母不为零.
总结:
求二次根式中字母的取值范围的基本依据:
①被开方数不小于0;
②分母中有字母时,要保证分母不为0.
1.下列各式: .
一定是二次根式的有 ( )
A.3个 B.4个 C.5个 D.6个
B
2.(1)若式子 在实数范围内有意义,则x的取值
范围是_______;
(2)若式子 在实数范围内有意义,则x的
取值范围是___________.
x ≥1
x ≥0且x≠2
二次根式的实质是表示一个非负数(或式)的算术平方根.对于任意一个二次根式 ,我们知道:
(1)a为被开方数,为保证其有意义,可知a≥0;
(2) 表示一个数或式的算术平方根,可知 ≥0.
二次根式的被开方数非负
二次根式的值非负
二次根式的双重非负性
3 若 ,求a -b+c的值.
解:
由题意可知a-2=0,b-3=0,c-4=0,
解得a=2,b=3,c=4.
所以a-b+c=2-3+4=3.
总结:多个非负数的和为零,则可得每个非负数均为零.初中阶段学过的非负数主要有绝对值、偶次幂及二次根式.
4 已知y= ,求3x+2y的算术平方根.
解:由题意得
∴x=3,∴y=8,
∴3x+2y=25.
∵25的算术平方根为5,
∴3x+2y的算术平方根为5.
五、归纳总结
本节课主要学习了二次根式的定义及被开方数的取值范围.
(1)本节课你学习了哪些知识?
(2)利用本节课知识,你能解决什么问题?
利用本节课知识,解决了使二次根式在实数范围内有意义的被开方数的取值范围问题,此问题在计算中经常作为隐含条件给出,注意合理应用.
2.式子 有意义的条件是 ( )
A.x>2 B.x≥2 C.x<2 D.x≤2
3.当x=____时,二次根式 取最小值,其最小值
为______.
1. 下列式子中,不属于二次根式的是( )
C
A
-1
0
4.当a是怎样的实数时,下列各式在实数范围内有
意义?
5.(1)若二次根式 有意义,求m的取值范围.
解:由题意得m-2≥0且m2-4≠0,
解得m≥2且m≠-2,m≠2,
∴m>2.
(2)无论x取任何实数,代数式 都有意义,求m的取值范围.
解:由题意得x2+6x+m≥0,
即(x+3)2+m-9≥0.
∵(x+3)2≥0,
∴m-9≥0,即m≥9.
