2021年中考数学二轮复习:常见旋转模型知识点总结(PDF版)
文档属性
| 名称 | 2021年中考数学二轮复习:常见旋转模型知识点总结(PDF版) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 18:24:53 | ||
图片预览

文档简介
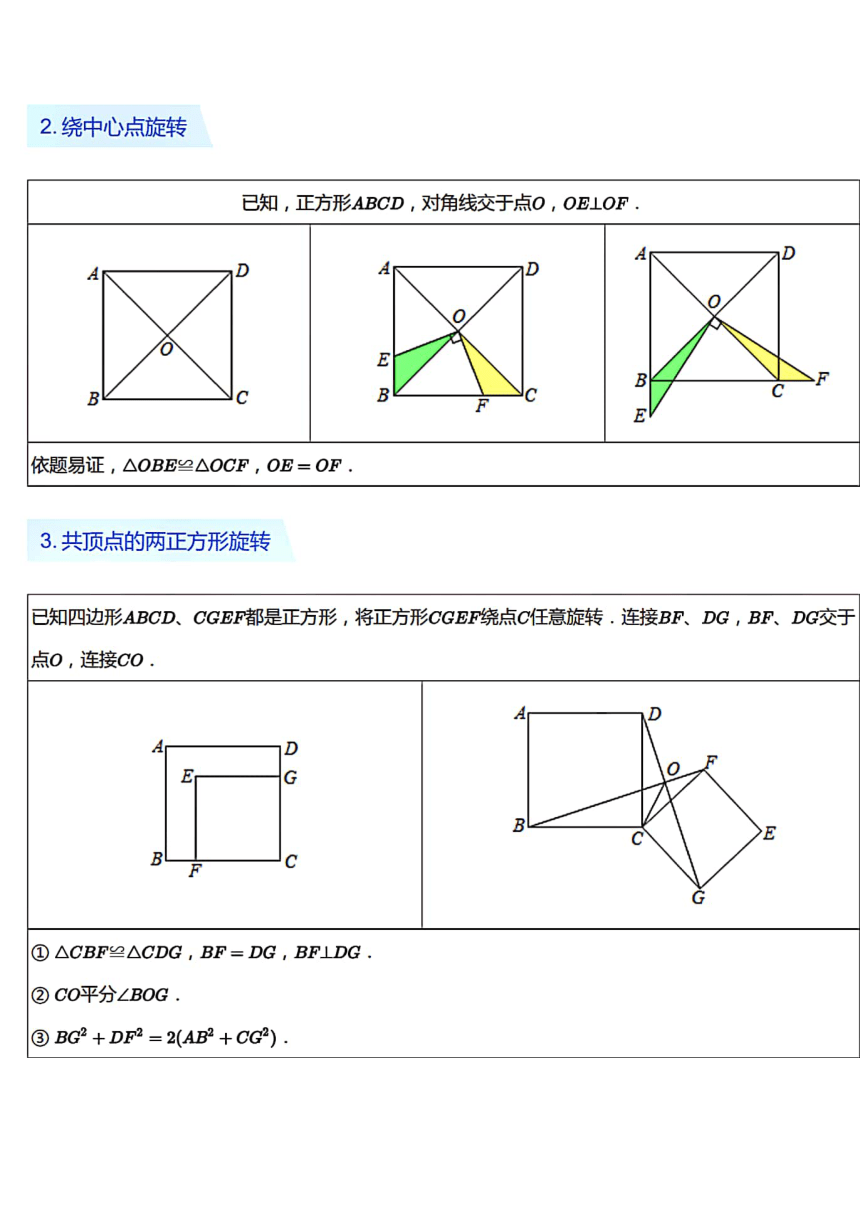
三、正方形中的旋转
绕顶点旋转90°
已知,正方形ABCD,点B是边CD上一点
D
E
B
C
C
将△ADB绕点A顺时针旋转90得到△ABP
则△EAF为等腰直角三角形,S
四边形AFCE=“正方形ABCD
将△ADE绕点D逆时针旋转90°得到△CDF
则△EDF为等腰直角三角形
已知,正方形ABCD,点E是正方形内一点
D
E
E
C
F
将△ABE绕点B顺时针旋转9得到△CBF,△EBF为等腰直角三角形
将△ABE绕点A逆时针旋转90得到△ADF,△EAF为等腰直角三角形
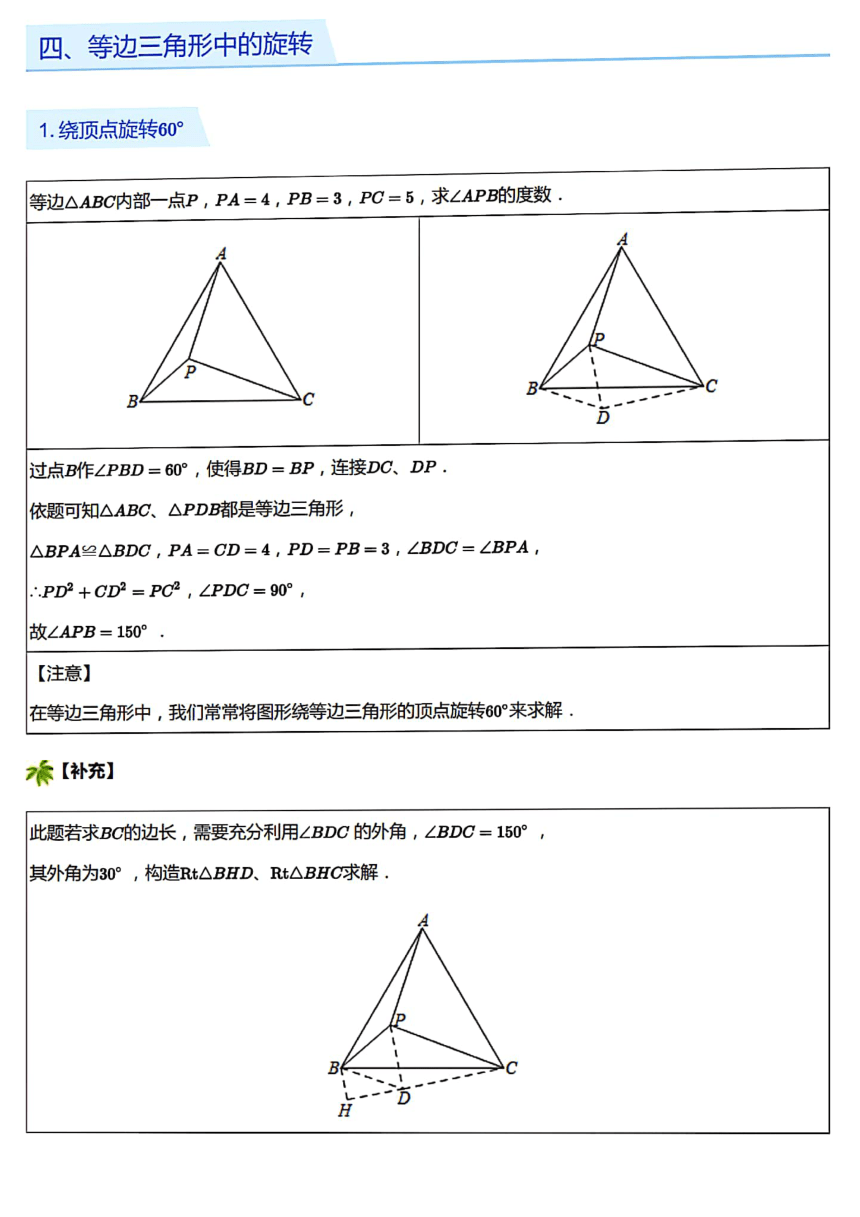
2.绕中心点旋转
已知,正方形ABCD,对角线交于点O,OE⊥OF
C
B
E
依题易证,△OBE≌△OCF,OE=OF
3.共顶点的两正方形旋转
已知四边形ABCD、CGBF都是正方形,将正方形GGEF绕点C任意旋转.连接BF、DG,BF、DG交于
点O,连接CO
G
E
①△CBF≌△CDG,BF=DG,
BFLDG
②CO平分∠BOG
③BG2+DF2=2(AB2+Ca2)
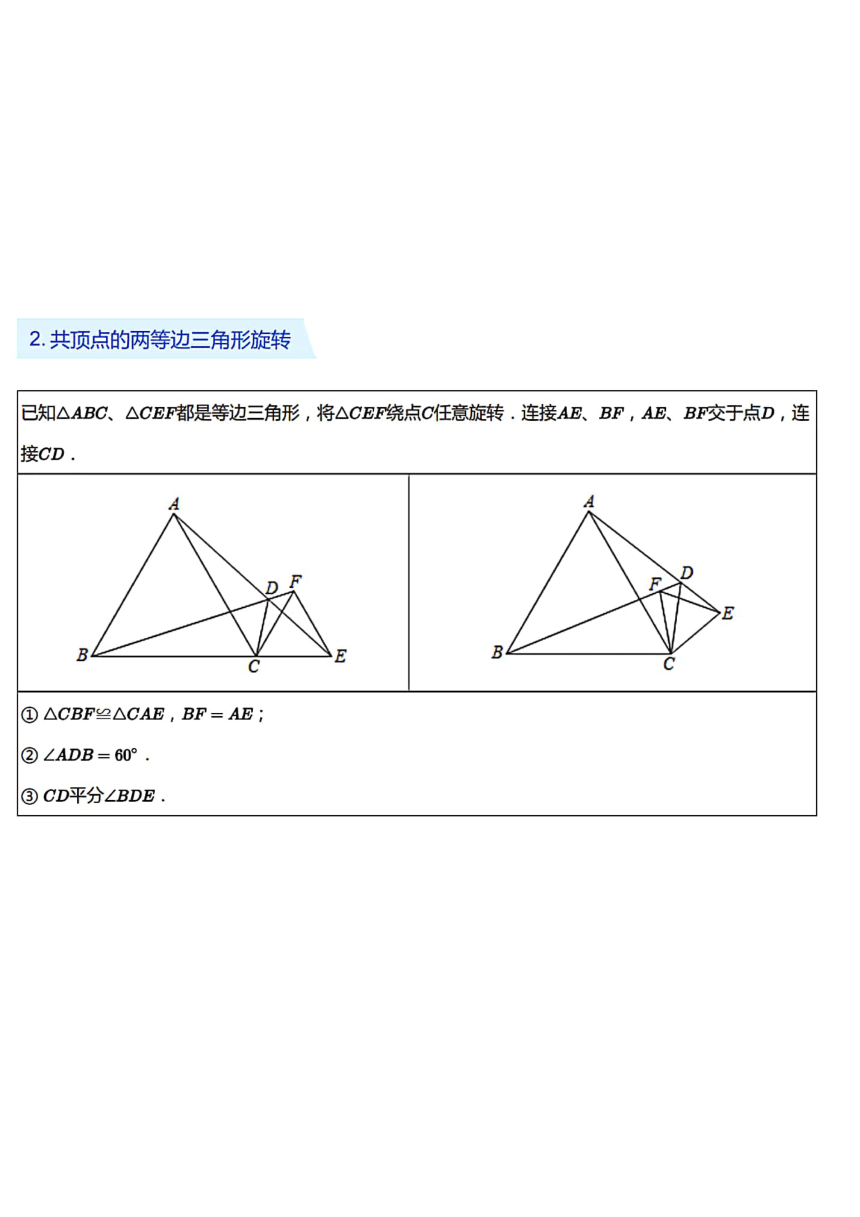
四、等边三角形中的旋转
1.绕页点旋转60°
等边△ABC内部一点P,PA=4,PB=3,PC=5,求∠APB的度数
过点B作∠PBD=60°,使得BD=BP,连接DC、DP
依题可知△ABC、△PDB都是等边三角形
△BPA≌△BDC,PA=CD=4,PD=PB=3,∠BDC=∠BPA
PD2+CD2=PC2,∠PDC=90°,
故∠APB=150°
在等边三角形中,我们常常将图形绕等边三角形的顶点旋转60°来求解
【补充】
此题若求BC的边长,需要充分利用∠BDC的外角,∠BDC=150°
其外角为30°,构造R△BD、R△BHC求解
C
H
2.共顶点的两等边三角形旋转
已知△ABC、△CEF都是等边三角形,将△CEF绕点C任意旋转.连接AEB、BF,AE、B交于点D,连
接CD
E
①△CBF≌△CAE,BF=AE
②∠ADB=60°
③CD平分∠BDE
手拉手旋转模型正向运用
会等边三角形中的手拉手旋转模型
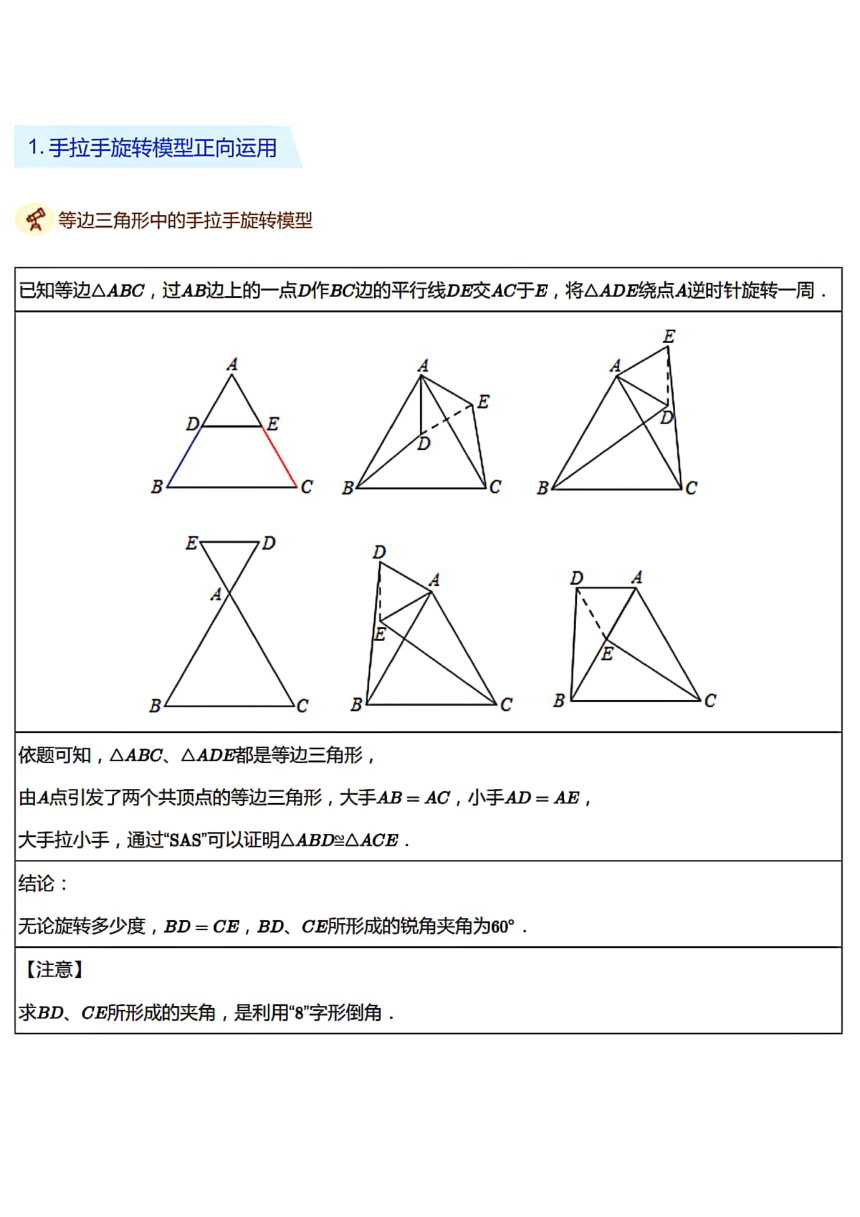
已知等边△ABC,过AB边上的一点D作BC边的平行线DB交AC于E,将△ADE绕点A逆时针旋转一周
E
A
E
B
C
C
依题可知,△ABC、△ADB都是等边三角形,
由A点引发了两个共顶点的等边三角形,大手AB=AC,小手AD=AE
大手拉小手,通过SAS可以证明△ABD≌△ACE
结论
无论旋转多少度,BD=CB,BD、CE所形成的锐角夹角为6
注意】
求BD、CE所形成的夹角,是利用8"字形倒角
绕顶点旋转90°
已知,正方形ABCD,点B是边CD上一点
D
E
B
C
C
将△ADB绕点A顺时针旋转90得到△ABP
则△EAF为等腰直角三角形,S
四边形AFCE=“正方形ABCD
将△ADE绕点D逆时针旋转90°得到△CDF
则△EDF为等腰直角三角形
已知,正方形ABCD,点E是正方形内一点
D
E
E
C
F
将△ABE绕点B顺时针旋转9得到△CBF,△EBF为等腰直角三角形
将△ABE绕点A逆时针旋转90得到△ADF,△EAF为等腰直角三角形
2.绕中心点旋转
已知,正方形ABCD,对角线交于点O,OE⊥OF
C
B
E
依题易证,△OBE≌△OCF,OE=OF
3.共顶点的两正方形旋转
已知四边形ABCD、CGBF都是正方形,将正方形GGEF绕点C任意旋转.连接BF、DG,BF、DG交于
点O,连接CO
G
E
①△CBF≌△CDG,BF=DG,
BFLDG
②CO平分∠BOG
③BG2+DF2=2(AB2+Ca2)
四、等边三角形中的旋转
1.绕页点旋转60°
等边△ABC内部一点P,PA=4,PB=3,PC=5,求∠APB的度数
过点B作∠PBD=60°,使得BD=BP,连接DC、DP
依题可知△ABC、△PDB都是等边三角形
△BPA≌△BDC,PA=CD=4,PD=PB=3,∠BDC=∠BPA
PD2+CD2=PC2,∠PDC=90°,
故∠APB=150°
在等边三角形中,我们常常将图形绕等边三角形的顶点旋转60°来求解
【补充】
此题若求BC的边长,需要充分利用∠BDC的外角,∠BDC=150°
其外角为30°,构造R△BD、R△BHC求解
C
H
2.共顶点的两等边三角形旋转
已知△ABC、△CEF都是等边三角形,将△CEF绕点C任意旋转.连接AEB、BF,AE、B交于点D,连
接CD
E
①△CBF≌△CAE,BF=AE
②∠ADB=60°
③CD平分∠BDE
手拉手旋转模型正向运用
会等边三角形中的手拉手旋转模型
已知等边△ABC,过AB边上的一点D作BC边的平行线DB交AC于E,将△ADE绕点A逆时针旋转一周
E
A
E
B
C
C
依题可知,△ABC、△ADB都是等边三角形,
由A点引发了两个共顶点的等边三角形,大手AB=AC,小手AD=AE
大手拉小手,通过SAS可以证明△ABD≌△ACE
结论
无论旋转多少度,BD=CB,BD、CE所形成的锐角夹角为6
注意】
求BD、CE所形成的夹角,是利用8"字形倒角
同课章节目录
