《实数》课件2（共15张ppt）

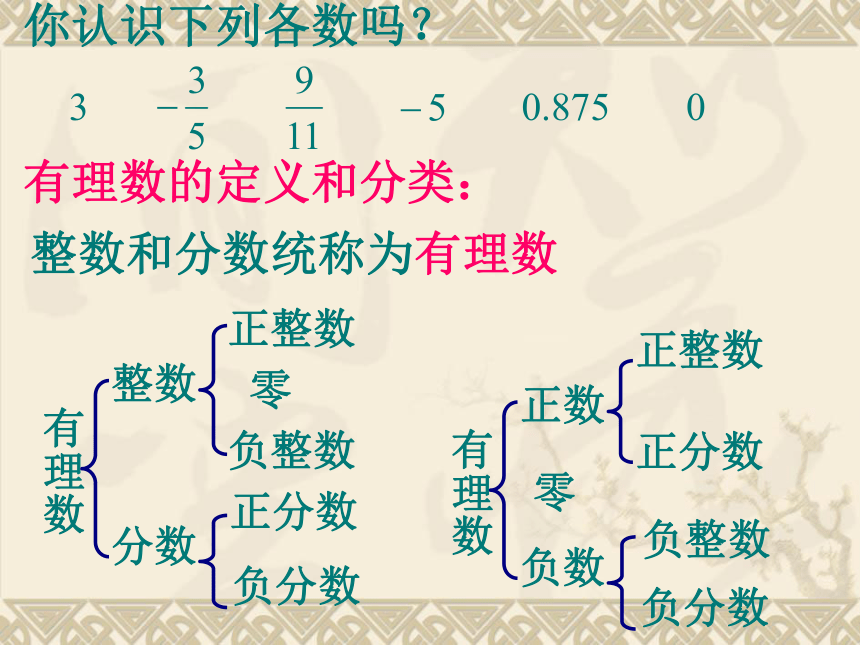
你认识下列各数吗？
有理数的定义和分类：
有理数
整数
分数
正整数
零
负整数
正分数
负分数
有理数
正数
负数
正整数
零
负整数
正分数
负分数
整数和分数统称为有理数
引入
把下列各数写成小数的形式：
有限小数
无限循环小数
有限小数和无限循环小数都是有理数
任何一个分数都可以表示成有限小数或无限循环小数的形式
下面方格网中，它们相邻的行距、列距都是1.横纵线相交形成的点叫做格点，以其中4个格点为顶点连接成一个正方形，叫做格点正方形。
（1）有面积分别为1、4、9的格点正方形吗？
（2）有面积为2的格点正方形吗？
是一个怎样的数呢？
探究：
把下列各数写成小数的形式：
上面这些数都是无限不循环小数
无限不循环小数叫做无理数
你能举出是无理数的例子吗？
１．圆周率 及一些含有 的数
２．开不尽方的数
３ 有一定的规律，但是属于不循环的无限小数

无理数的特征:
注意:带根号的数不一定是无理数
有理数和无理数统称为实数
归纳
实数的分类
实数
有理数
无理数
整数
分数
有限小数或
无限循环小数
无限不循环小数
你还有其它分类方法吗？
(定义式)
归纳
实数的分类
实数
正实数
负实数
正有理数
正无理数
你知道怎样区分有理数和无理数吗？
0
负无理数
负有理数
(性质)
例题巩固
1、下列各数中，哪些是有理数，哪
些是无理数？
巩固
2、下列各数 ， ， ， ，
， 中，有理数的个数有( )
A 2个 B 3个
C 4个 D 5个
3、判断：
1.实数不是有理数就是无理数（ ）
2.无理数都是无限不循环小数。（ ）
3.无理数都是无限小数。（ ）
4.带根号的数都是无理数（ ）
5.无理数一定都带根号。（ ）
6.两个无理数之积不一定是无理数（ ）
7.两个无理数之和一定是无理数。（ ）
×
×
×
8.有理数与无理数之和一定是无理数 ( )
巩固
4、在 ， ， ，
， ， 中，无理数分别
是 。
巩固
5、把下列各数分别填在相应的集合中：
有理数集合
无理数集合
…
…
小结
1、本节课你学了什么知识?
2、你有什么体会?
实数的定义
实数的分类
有理数
无理数
有限小数或
无限循环小数
无限不循环小数
(定义、正负)