《一元一次不等式组》课件1(共20张ppt)
文档属性
| 名称 | 《一元一次不等式组》课件1(共20张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
某校今年冬季烧煤取暖时间为4个月.如果每个
月比计划多烧5吨煤,
那么取暖用煤总量将超
过100吨;如果每月比计划少烧5吨煤,那么取
暖用煤总量不足68吨,该校计划每月烧煤多少
吨?
设该校计划每月烧煤x吨,根据题意,得
未知数x同时满足①
②两个条件,把①
②两个不
等式合在一起,就组成一个一元一次不等式组,
记作:
4(x+5)>100
①
且
4(x-5)<68
②
4(x+5)>100
4(x-5)<68
{
引例
一般地,
关于同一未知数的几个一元一次不等式
合在一起,就组成一个
一元一次不等式组
如何求一元一次不等式组的解集呢?
4(x+5)>100
①
4(x-5)<68
②
{
解不等式①得:
x>20
解不等式②得:
x<22
20
22
同时满足不等式①、②的未知数x是
两个不等式的公共部分,在数轴上
表示为
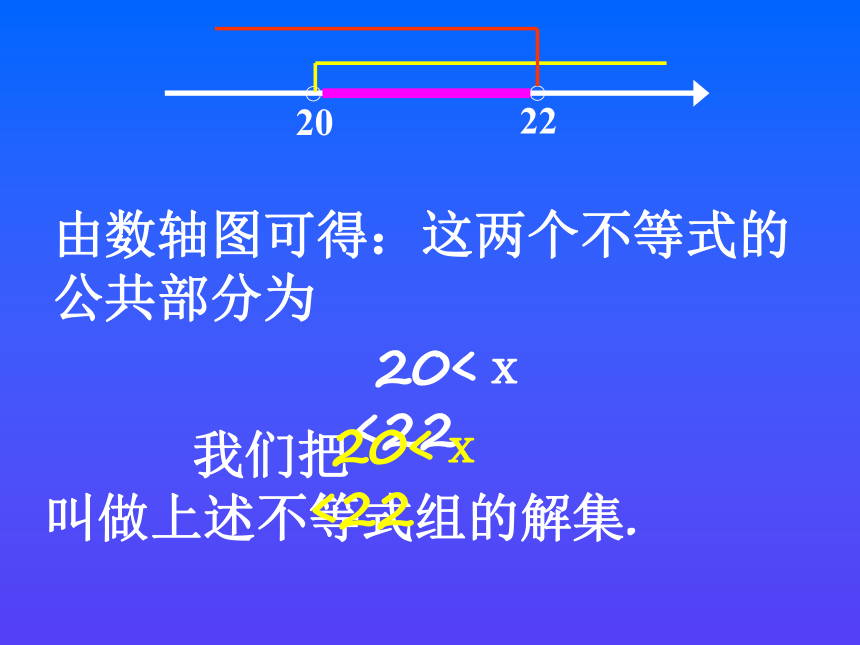
由数轴图可得:这两个不等式的
公共部分为
20
22
20<x<22
我们把
叫做上述不等式组的解集.
20<x<22
一般地,
不等式组中所有不等式的解集
的公共部分叫做不等式组的解集.
求不等式组解集的过程叫做
解不等式组
2
1
3
0
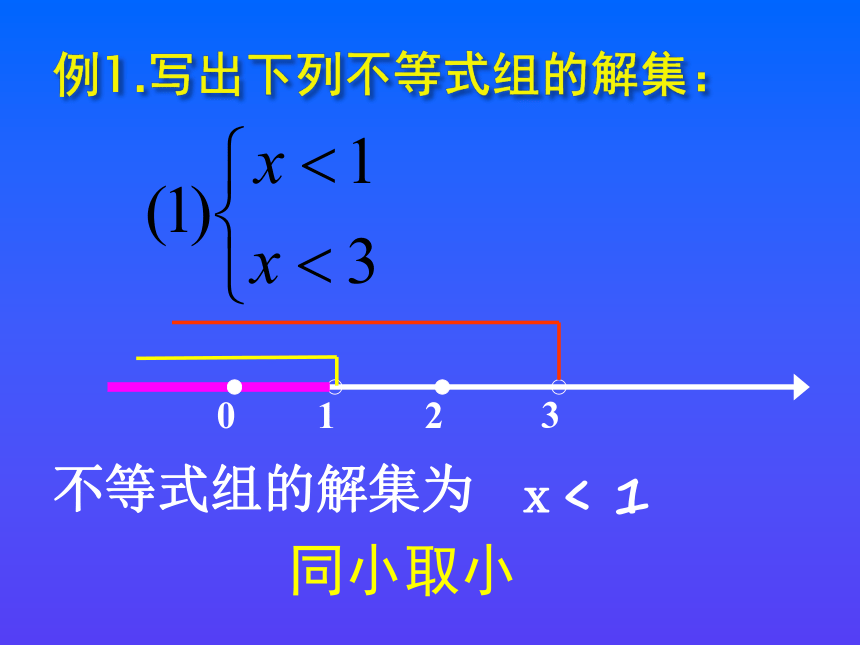
不等式组的解集为
x<
1
同小取小
2
1
3
0
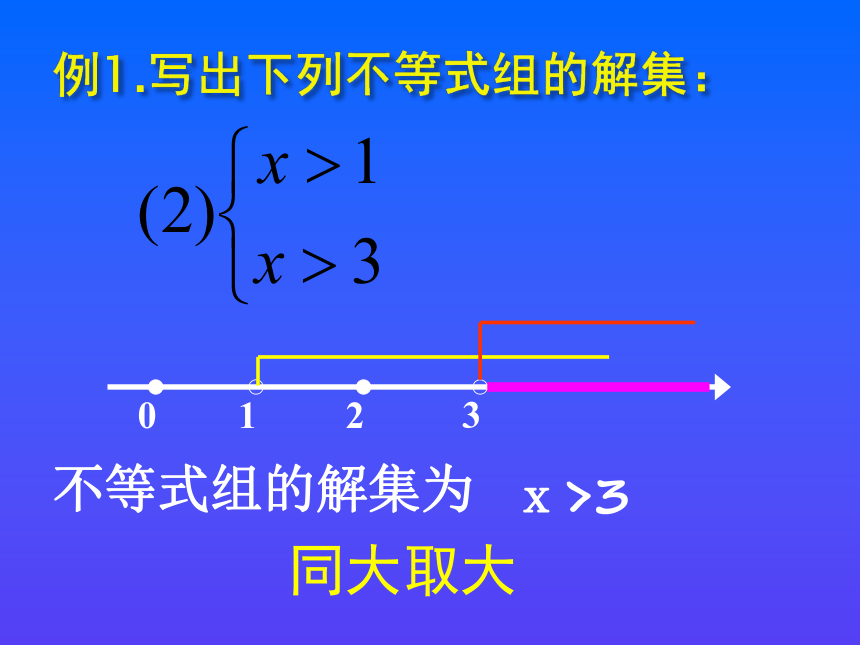
不等式组的解集为
x>3
同大取大
2
1
3
0
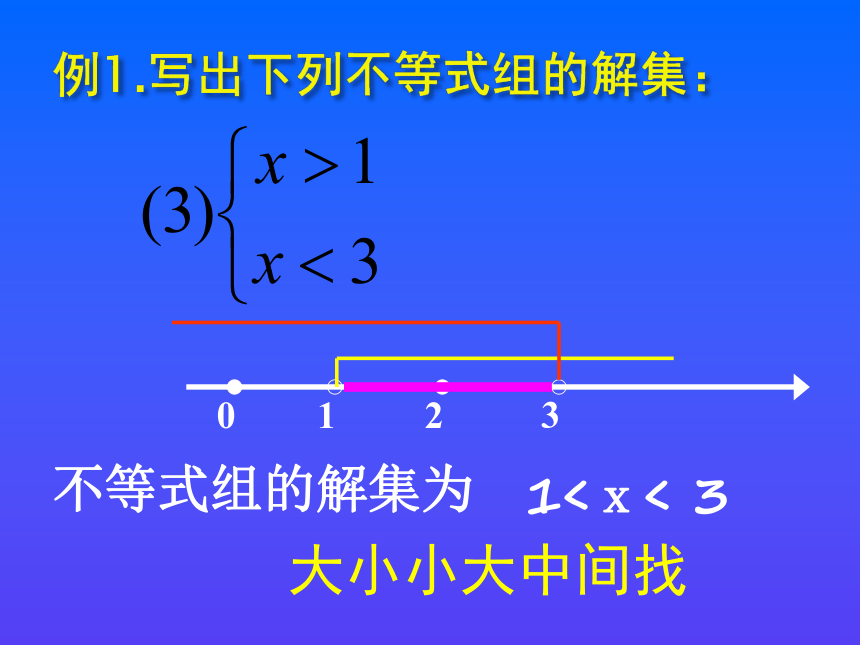
不等式组的解集为
1<x<
3
大小小大中间找
2
1
3
0
不等式组的解集为空集
即:不等式组无解
大大小小找不到
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
x>a
x>
b
x<a
x<b
x<a
x>
b
x>a
x<b
a
a
a
a
a
a
a
a
b
b
b
b
b
b
b
b
x>
b
(同大取大)
x<a
(同小取小)
a<x<b
(交叉取中间)
无解
(无公共部分)
一元一次不等式组的解集图析
(a<b
)
如果a=b呢?
2x+1
<
-1
①
3-x≥1
②
{
解不等式①得:
x<
-1
解不等式②得:
x≤2
在数轴上表示不等式①、②的解集:
例2.解不等式组:
解:
1
0
2
-1
所以不等式组的解集为:
x<
-1
例3.解不等式组:
①
②
解:解不等式①,得
解不等式②,得
不等式组的解集是
2
0
4
2.5
1
3
解一元一次不等式组的方法:
2.(1)利用数轴找几个解集的公共部分:
(2)利用规律:
大大取较大,小小取较小;大小小大取中间,大大小小解不了.
1.求出不等式组中各个不等式的解集;
3.写出这个不等式组的解集;
选择题:
(1)不等式组
的解集是(
)
A.x
≥2,
D.x
=2.
B.x≤2,
C.
无解,
(2)不等式组
的整数解是(
)
≤1
D.
x≤1.
A.
0,
1
,
B.
0
,
C.
1,
D
C
≥2
≤2
练一练
D.不能确定.
A.
-2,0,
-1
,
B.
-2
C.
-2,-1
(3)不等式组
的负整数解是(
)
≥-2,
(4)不等式组
的解集在数轴上
表示为
(
)
≥-2,
A.
D.
C.
B.
C
B
-5
-2
-5
-2
-5
-2
-5
-2
例4.解不等式:
解法一:
解不等式①得:
解不等式②得:
所以不等式组的解集为:
解法二:
所以不等式组的解集为:
1.关键概念:
一元一次不等式组;不等式组的解集.
2.学法指导:
数形结合法,依靠数轴求不等式组的解集.
会运用不等式组的知识解决实际问题,并注意检验结果的合理性.
某校今年冬季烧煤取暖时间为4个月.如果每个
月比计划多烧5吨煤,
那么取暖用煤总量将超
过100吨;如果每月比计划少烧5吨煤,那么取
暖用煤总量不足68吨,该校计划每月烧煤多少
吨?
设该校计划每月烧煤x吨,根据题意,得
未知数x同时满足①
②两个条件,把①
②两个不
等式合在一起,就组成一个一元一次不等式组,
记作:
4(x+5)>100
①
且
4(x-5)<68
②
4(x+5)>100
4(x-5)<68
{
引例
一般地,
关于同一未知数的几个一元一次不等式
合在一起,就组成一个
一元一次不等式组
如何求一元一次不等式组的解集呢?
4(x+5)>100
①
4(x-5)<68
②
{
解不等式①得:
x>20
解不等式②得:
x<22
20
22
同时满足不等式①、②的未知数x是
两个不等式的公共部分,在数轴上
表示为
由数轴图可得:这两个不等式的
公共部分为
20
22
20<x<22
我们把
叫做上述不等式组的解集.
20<x<22
一般地,
不等式组中所有不等式的解集
的公共部分叫做不等式组的解集.
求不等式组解集的过程叫做
解不等式组
2
1
3
0
不等式组的解集为
x<
1
同小取小
2
1
3
0
不等式组的解集为
x>3
同大取大
2
1
3
0
不等式组的解集为
1<x<
3
大小小大中间找
2
1
3
0
不等式组的解集为空集
即:不等式组无解
大大小小找不到
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
x>a
x>
b
x<a
x<b
x<a
x>
b
x>a
x<b
a
a
a
a
a
a
a
a
b
b
b
b
b
b
b
b
x>
b
(同大取大)
x<a
(同小取小)
a<x<b
(交叉取中间)
无解
(无公共部分)
一元一次不等式组的解集图析
(a<b
)
如果a=b呢?
2x+1
<
-1
①
3-x≥1
②
{
解不等式①得:
x<
-1
解不等式②得:
x≤2
在数轴上表示不等式①、②的解集:
例2.解不等式组:
解:
1
0
2
-1
所以不等式组的解集为:
x<
-1
例3.解不等式组:
①
②
解:解不等式①,得
解不等式②,得
不等式组的解集是
2
0
4
2.5
1
3
解一元一次不等式组的方法:
2.(1)利用数轴找几个解集的公共部分:
(2)利用规律:
大大取较大,小小取较小;大小小大取中间,大大小小解不了.
1.求出不等式组中各个不等式的解集;
3.写出这个不等式组的解集;
选择题:
(1)不等式组
的解集是(
)
A.x
≥2,
D.x
=2.
B.x≤2,
C.
无解,
(2)不等式组
的整数解是(
)
≤1
D.
x≤1.
A.
0,
1
,
B.
0
,
C.
1,
D
C
≥2
≤2
练一练
D.不能确定.
A.
-2,0,
-1
,
B.
-2
C.
-2,-1
(3)不等式组
的负整数解是(
)
≥-2,
(4)不等式组
的解集在数轴上
表示为
(
)
≥-2,
A.
D.
C.
B.
C
B
-5
-2
-5
-2
-5
-2
-5
-2
例4.解不等式:
解法一:
解不等式①得:
解不等式②得:
所以不等式组的解集为:
解法二:
所以不等式组的解集为:
1.关键概念:
一元一次不等式组;不等式组的解集.
2.学法指导:
数形结合法,依靠数轴求不等式组的解集.
会运用不等式组的知识解决实际问题,并注意检验结果的合理性.
