【课时作业】第三章 圆(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
2020-2021学年九年级数学下册单元综合复习(北师版)
第三章 圆
一、选择题
1.已知⊙O的半径为3.6cm,线段OA=cm,则点A与⊙O的位置关系是( )
A.点A在⊙O外 B.点A在⊙O上
C.点A在⊙O内 D.不能确定
2.如图,P是⊙O外一点,PA,PB分别交⊙O于C,D两点,已知,的度数分别为88°,32°,则∠P的度数是( )
A.26° B.28° C.30° D.32°
3.如图,AB是⊙O的直径,过点B作一弦BC,且OD⊥BC于点E.若BC=8cm,∠ABC=30°,则DE的长为( )
A.cm B.cm C.4cm D.2cm
4.如图,将⊙O沿弦AB折叠,恰好经过圆心O,若⊙O的半径为3,则劣的长为( )
A.π B.π C.2π D.3π
5.以坐标原点O为圆心,作半径为2的圆,若直线y=-x+b与⊙O相交,则b的取值范围是( )
A.0≤b<2 B.-2≤b≤2
C.-26.如图,⊙O的半径OD垂直于弦AB,垂足为C,连接AO并延长交⊙O于点E,连接BE,CE.若AB=8,CD=2,则△BCE的面积为( )
A.12 B.15 C.16 D.18
7.如图,正方形ABCD内接于半径为2的⊙O,则图中阴影部分的面积为( )
A.π+1 B.π+2 C.π-1 D.π-2
8.如图,过圆外一点B引圆O的两条切线BA,BD,切点分别是A,D,连接AO并延长,交BD的延长线于点C,若AB=5,BC=13,则圆O的半径为( )
A. B. C.3 D.
9.如图,四边形ABCD内接于⊙O,AE⊥CB交CB的延长线于点E,若BA平分∠DBE,AD=5,CE=,则AE的长是( )
A.3 B.3 C.4 D.2
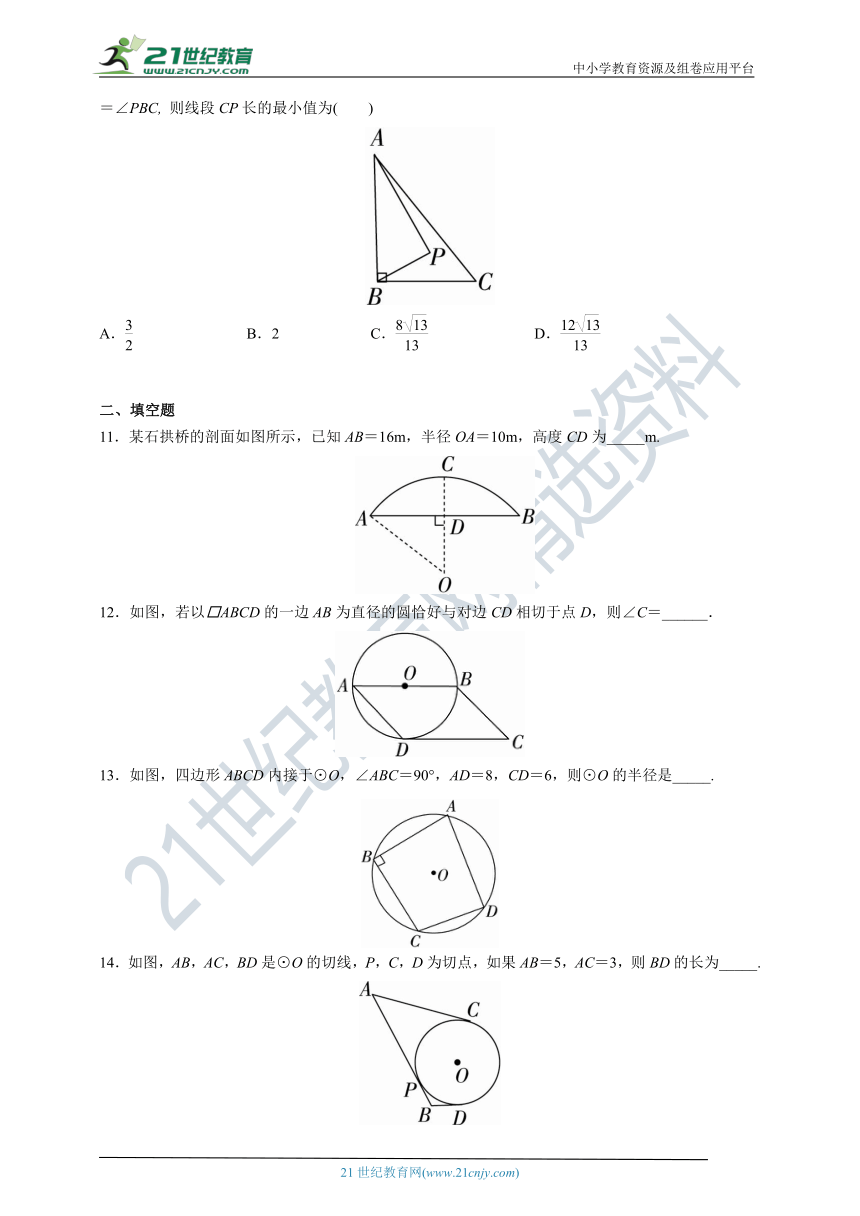
10.如图,在Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC, 则线段CP长的最小值为( )
A. B.2 C. D.
二、填空题
11.某石拱桥的剖面如图所示,已知AB=16m,半径OA=10m,高度CD为_____m.
12.如图,若以□ABCD的一边AB为直径的圆恰好与对边CD相切于点D,则∠C=______.
13.如图,四边形ABCD内接于⊙O,∠ABC=90°,AD=8,CD=6,则⊙O的半径是_____.
14.如图,AB,AC,BD是⊙O的切线,P,C,D为切点,如果AB=5,AC=3,则BD的长为_____.
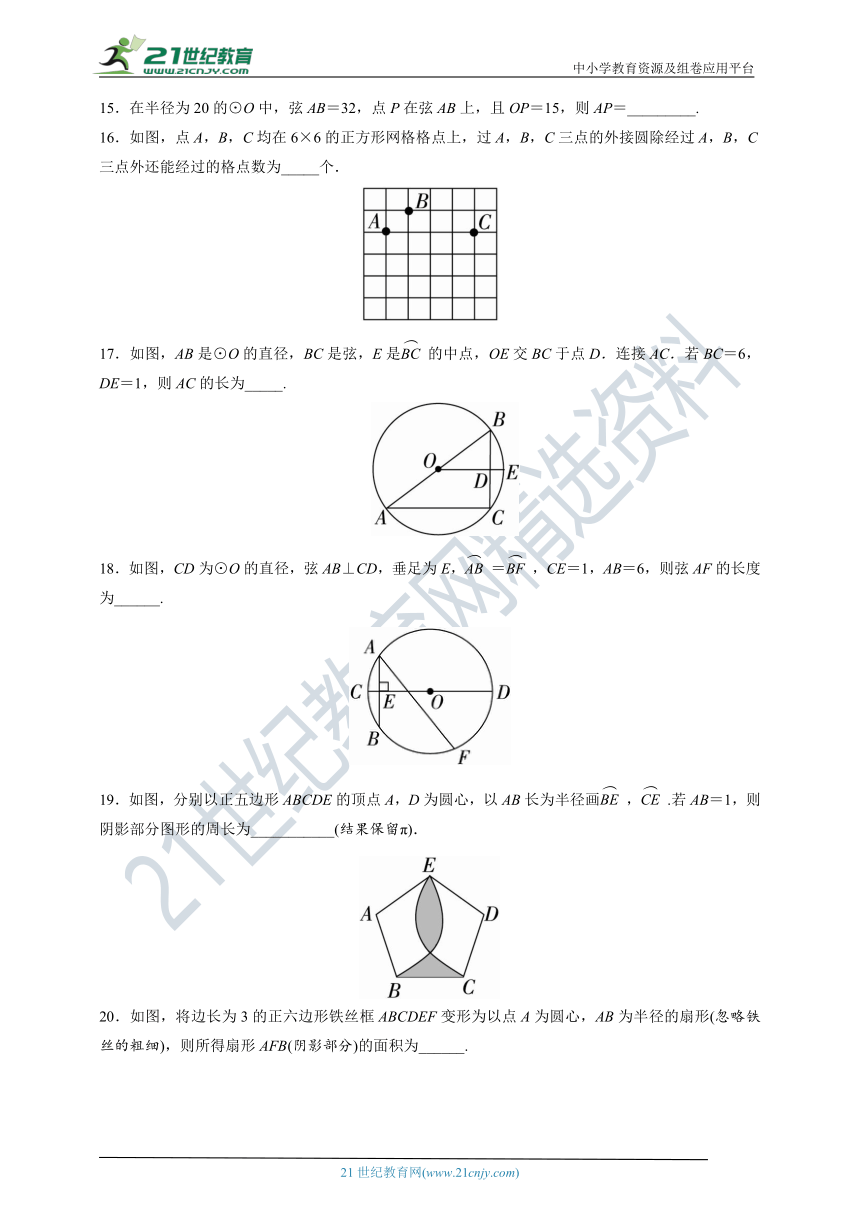
15.在半径为20的⊙O中,弦AB=32,点P在弦AB上,且OP=15,则AP=_________.
16.如图,点A,B,C均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为_____个.
17.如图,AB是⊙O的直径,BC是弦,E是的中点,OE交BC于点D.连接AC.若BC=6,DE=1,则AC的长为_____.
18.如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,=,CE=1,AB=6,则弦AF的长度为______.
19.如图,分别以正五边形ABCDE的顶点A,D为圆心,以AB长为半径画,.若AB=1,则阴影部分图形的周长为___________(结果保留π).
20.如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得扇形AFB(阴影部分)的面积为______.
三、解答题
21.如图,已知A,B,C为⊙O上三点,M,N分别为AB,AC的中点,OM的延长线交⊙O于点D,ON的延长线交⊙O于点E,DE交AB于点F,交AC于点G.求证:AF=AG.
22.如图,正方形ABCD内接于⊙O,M为的中点,连接BM,CM.
(1)求证:BM=CM;
(2)当⊙O的半径为2时,求的长.
22.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
23.如图,⊙O的直径为AB,点C在圆周上(异于点A,B),AD⊥CD.
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
24.如图①,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
(1)求证:MD=ME;
(2)如图②,连OD,OE,当∠C=30°时,求证:四边形ODME是菱形.
图① 图②
25.如图,在△ABC中,∠ACB=90°,O是边AC上一点,以点O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使BF=EF,EF与AC交于点G.
(1)试判断直线EF与⊙O的位置关系,并说明理由;
(2)若OA=2,∠A=30°,求图中阴影部分的面积.
26.如图,AB是⊙O的直径,点C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连接BD交CF于点G,连接CD,AD,BF.
(1)求证:△BFG≌△CDG;
(2)若AD=BE=2,求BF的长.
参 考 答 案
1. C 2. B 3. B 4. C 5. D 6. A 7. D 8. B 9. D 10. B
11. 4
12. 45°
13. 5
14. 2
15. 7或25
16. 5
17. 8
18.
19. π+1
20. 18
21. 证明:∵M,N分别为AB,AC的中点,∴OM⊥AB,ON⊥AC,即∠DMF=∠ENG=90°.又∵OD=OE,∴∠D=∠E.∴∠DFM=∠EGN,即∠AFG=∠AGF.∴AF=AG.
21. (1)证明:∵四边形ABCD是正方形,∴AB=CD,∴=.∵M为的中点,∴=,∴=,∴BM=CM.
(2)解:连接OB,OM.由题意知∠BOM=135°,r=2,所以当为劣弧时,l==π;当为优弧时,l==π.综上所述,的长为π 或π.
22. (1)解:∵BC=DC,∴∠CBD=∠CDB=39°.∵∠BAC=∠CDB=39°,∠CAD=∠CBD=39°,∴∠BAD=∠BAC+∠CAD=39°+39°=78°.
(2)证明:∵EC=BC,∴∠CEB=∠CBE,而∠CEB=∠2+∠BAE,∠CBE=∠1+∠CBD,∴∠2+∠BAE=∠1+∠CBD.∵∠BAE=∠BDC=∠CBD,∴∠1=∠2.
23. (1)解:∵AB是⊙O的直径,点C在⊙O上,∴∠ACB=90°.又∵BC=3,AB=5,∴AC=4.
(2)证明:连接OC.∵AC是∠DAB的平分线,∴∠DAC=∠BAC.又∵AD⊥DC,∴∠ADC=∠ACB=90°,∴△ADC∽△ACB,∴∠ACD=∠ABC.又∵OA=OC,∴∠OAC=∠OCA.∵∠OAC+∠OBC=90°,∴∠OCA+∠ACD=∠OCD=90°,即DC⊥CO,∴直线CD是⊙O的切线.
24. 解:连接DE.(1)在Rt△ABC中,点M是AC的中点,∴MA=MB,∴∠A=∠MBA.∵四边形ABED是圆内接四边形,∴∠ADE+∠ABE=180°,而∠ADE+∠MDE=180°,∴∠MDE=∠MBA;同理可得∠MED=∠A,∴∠MDE=∠MED,∴MD=ME.
(2)∵∠C=30°,∴∠A=60°,∴∠ABM=60°,∴△OAD和△OBE为等边三角形,∴∠BOE=60°,∴∠BOE=∠A,∴OE∥AC,同理可得OD∥BM,∴四边形DOEM为平行四边形,而OD=OE,∴四边形ODME是菱形.
25. 解:(1)连接OE,∵OA=OE,∴∠A=∠AEO,∵BF=EF,∴∠B=∠BEF,∵∠ACB=90°,∴∠A+∠B=90°,∴∠AEO+∠BEF=90°,∴∠OEG=90°,即EF⊥OE,∴EF是⊙O的切线.
(2)∵AD是⊙O的直径,∴∠AED=90°,∵∠A=30°,∴∠EOD=60°,∴∠EGO=30°,∵AO=2,∴OE=2,∴EG=2,∴阴影部分的面积=×2×2-=2-π.
26. (1)证明:∵C是的中点,∴=.∵AB是⊙O的直径,且CF⊥AB,∴=,∴=,∴CD=BF.在△BFG和△CDG中,∴△BFC≌△CDG(AAS)
(2)解:如图,过点C作CH⊥AD,交AD的延长线于点H,连接AC,BC,∵=,∴∠HAC=∠BAC,∵CE⊥AB,∴CH=CE,∵AC=AC,∴Rt△AHC≌Rt△AEC(HL),∴AE=AH,∵CH=CE,CD=CB,∴Rt△CDH≌Rt△CBE(HL),∴DH=BE=2,∴AE=AH=AD+DH=2+2=4,∴AB=AE+BE=4+2=6,∵AB是⊙O的直径,∴∠ACB=90°,∴∠ACB=∠BEC=90°,∵∠EBC=∠ABC,∴△BEC∽△BCA,∴=,∴BC2=AB·BE=6×2=12,∴BF=BC=2.
_21?????????è?????(www.21cnjy.com)_
2020-2021学年九年级数学下册单元综合复习(北师版)
第三章 圆
一、选择题
1.已知⊙O的半径为3.6cm,线段OA=cm,则点A与⊙O的位置关系是( )
A.点A在⊙O外 B.点A在⊙O上
C.点A在⊙O内 D.不能确定
2.如图,P是⊙O外一点,PA,PB分别交⊙O于C,D两点,已知,的度数分别为88°,32°,则∠P的度数是( )
A.26° B.28° C.30° D.32°
3.如图,AB是⊙O的直径,过点B作一弦BC,且OD⊥BC于点E.若BC=8cm,∠ABC=30°,则DE的长为( )
A.cm B.cm C.4cm D.2cm
4.如图,将⊙O沿弦AB折叠,恰好经过圆心O,若⊙O的半径为3,则劣的长为( )
A.π B.π C.2π D.3π
5.以坐标原点O为圆心,作半径为2的圆,若直线y=-x+b与⊙O相交,则b的取值范围是( )
A.0≤b<2 B.-2≤b≤2
C.-2
A.12 B.15 C.16 D.18
7.如图,正方形ABCD内接于半径为2的⊙O,则图中阴影部分的面积为( )
A.π+1 B.π+2 C.π-1 D.π-2
8.如图,过圆外一点B引圆O的两条切线BA,BD,切点分别是A,D,连接AO并延长,交BD的延长线于点C,若AB=5,BC=13,则圆O的半径为( )
A. B. C.3 D.
9.如图,四边形ABCD内接于⊙O,AE⊥CB交CB的延长线于点E,若BA平分∠DBE,AD=5,CE=,则AE的长是( )
A.3 B.3 C.4 D.2
10.如图,在Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC, 则线段CP长的最小值为( )
A. B.2 C. D.
二、填空题
11.某石拱桥的剖面如图所示,已知AB=16m,半径OA=10m,高度CD为_____m.
12.如图,若以□ABCD的一边AB为直径的圆恰好与对边CD相切于点D,则∠C=______.
13.如图,四边形ABCD内接于⊙O,∠ABC=90°,AD=8,CD=6,则⊙O的半径是_____.
14.如图,AB,AC,BD是⊙O的切线,P,C,D为切点,如果AB=5,AC=3,则BD的长为_____.
15.在半径为20的⊙O中,弦AB=32,点P在弦AB上,且OP=15,则AP=_________.
16.如图,点A,B,C均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为_____个.
17.如图,AB是⊙O的直径,BC是弦,E是的中点,OE交BC于点D.连接AC.若BC=6,DE=1,则AC的长为_____.
18.如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,=,CE=1,AB=6,则弦AF的长度为______.
19.如图,分别以正五边形ABCDE的顶点A,D为圆心,以AB长为半径画,.若AB=1,则阴影部分图形的周长为___________(结果保留π).
20.如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得扇形AFB(阴影部分)的面积为______.
三、解答题
21.如图,已知A,B,C为⊙O上三点,M,N分别为AB,AC的中点,OM的延长线交⊙O于点D,ON的延长线交⊙O于点E,DE交AB于点F,交AC于点G.求证:AF=AG.
22.如图,正方形ABCD内接于⊙O,M为的中点,连接BM,CM.
(1)求证:BM=CM;
(2)当⊙O的半径为2时,求的长.
22.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
23.如图,⊙O的直径为AB,点C在圆周上(异于点A,B),AD⊥CD.
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
24.如图①,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
(1)求证:MD=ME;
(2)如图②,连OD,OE,当∠C=30°时,求证:四边形ODME是菱形.
图① 图②
25.如图,在△ABC中,∠ACB=90°,O是边AC上一点,以点O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使BF=EF,EF与AC交于点G.
(1)试判断直线EF与⊙O的位置关系,并说明理由;
(2)若OA=2,∠A=30°,求图中阴影部分的面积.
26.如图,AB是⊙O的直径,点C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连接BD交CF于点G,连接CD,AD,BF.
(1)求证:△BFG≌△CDG;
(2)若AD=BE=2,求BF的长.
参 考 答 案
1. C 2. B 3. B 4. C 5. D 6. A 7. D 8. B 9. D 10. B
11. 4
12. 45°
13. 5
14. 2
15. 7或25
16. 5
17. 8
18.
19. π+1
20. 18
21. 证明:∵M,N分别为AB,AC的中点,∴OM⊥AB,ON⊥AC,即∠DMF=∠ENG=90°.又∵OD=OE,∴∠D=∠E.∴∠DFM=∠EGN,即∠AFG=∠AGF.∴AF=AG.
21. (1)证明:∵四边形ABCD是正方形,∴AB=CD,∴=.∵M为的中点,∴=,∴=,∴BM=CM.
(2)解:连接OB,OM.由题意知∠BOM=135°,r=2,所以当为劣弧时,l==π;当为优弧时,l==π.综上所述,的长为π 或π.
22. (1)解:∵BC=DC,∴∠CBD=∠CDB=39°.∵∠BAC=∠CDB=39°,∠CAD=∠CBD=39°,∴∠BAD=∠BAC+∠CAD=39°+39°=78°.
(2)证明:∵EC=BC,∴∠CEB=∠CBE,而∠CEB=∠2+∠BAE,∠CBE=∠1+∠CBD,∴∠2+∠BAE=∠1+∠CBD.∵∠BAE=∠BDC=∠CBD,∴∠1=∠2.
23. (1)解:∵AB是⊙O的直径,点C在⊙O上,∴∠ACB=90°.又∵BC=3,AB=5,∴AC=4.
(2)证明:连接OC.∵AC是∠DAB的平分线,∴∠DAC=∠BAC.又∵AD⊥DC,∴∠ADC=∠ACB=90°,∴△ADC∽△ACB,∴∠ACD=∠ABC.又∵OA=OC,∴∠OAC=∠OCA.∵∠OAC+∠OBC=90°,∴∠OCA+∠ACD=∠OCD=90°,即DC⊥CO,∴直线CD是⊙O的切线.
24. 解:连接DE.(1)在Rt△ABC中,点M是AC的中点,∴MA=MB,∴∠A=∠MBA.∵四边形ABED是圆内接四边形,∴∠ADE+∠ABE=180°,而∠ADE+∠MDE=180°,∴∠MDE=∠MBA;同理可得∠MED=∠A,∴∠MDE=∠MED,∴MD=ME.
(2)∵∠C=30°,∴∠A=60°,∴∠ABM=60°,∴△OAD和△OBE为等边三角形,∴∠BOE=60°,∴∠BOE=∠A,∴OE∥AC,同理可得OD∥BM,∴四边形DOEM为平行四边形,而OD=OE,∴四边形ODME是菱形.
25. 解:(1)连接OE,∵OA=OE,∴∠A=∠AEO,∵BF=EF,∴∠B=∠BEF,∵∠ACB=90°,∴∠A+∠B=90°,∴∠AEO+∠BEF=90°,∴∠OEG=90°,即EF⊥OE,∴EF是⊙O的切线.
(2)∵AD是⊙O的直径,∴∠AED=90°,∵∠A=30°,∴∠EOD=60°,∴∠EGO=30°,∵AO=2,∴OE=2,∴EG=2,∴阴影部分的面积=×2×2-=2-π.
26. (1)证明:∵C是的中点,∴=.∵AB是⊙O的直径,且CF⊥AB,∴=,∴=,∴CD=BF.在△BFG和△CDG中,∴△BFC≌△CDG(AAS)
(2)解:如图,过点C作CH⊥AD,交AD的延长线于点H,连接AC,BC,∵=,∴∠HAC=∠BAC,∵CE⊥AB,∴CH=CE,∵AC=AC,∴Rt△AHC≌Rt△AEC(HL),∴AE=AH,∵CH=CE,CD=CB,∴Rt△CDH≌Rt△CBE(HL),∴DH=BE=2,∴AE=AH=AD+DH=2+2=4,∴AB=AE+BE=4+2=6,∵AB是⊙O的直径,∴∠ACB=90°,∴∠ACB=∠BEC=90°,∵∠EBC=∠ABC,∴△BEC∽△BCA,∴=,∴BC2=AB·BE=6×2=12,∴BF=BC=2.
_21?????????è?????(www.21cnjy.com)_
