2020——2021学年北师大版七年级数学下册 3.3 用图象表示的变量间关系课件(共32张)
文档属性
| 名称 | 2020——2021学年北师大版七年级数学下册 3.3 用图象表示的变量间关系课件(共32张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 22:55:33 | ||
图片预览









文档简介
第三章 变量之间的关系
第3课时 用图象表示的变量间关系
学习目标
1.经历从图象中分析变量之间关系的过程,进一步体会变量之间的关系.
2.结合具体情境理解图象上的点所表示的意义.
3.能从图象中获取变量之间关系的信息,感受几何直观的作用,并能用语言进行描述.
知识要点
知识点一:用图象表示两个变量间的关系
(1)用图象表示两个变量之间关系的方法叫做图象法.
(2)如图,在利用图象表示两个变量之间的关系时,通常用水平方向的数轴(称为横轴)上的点表示自变量,用竖直方向的数轴(称为纵轴)上的点来表示因变量.过图象上的一点向横轴作垂线,其垂足表示的数据就是自变量的一个取值,然后过该点再向纵轴作垂线,其垂足表示的数就是与自变量的值对应的因变量的一个值.
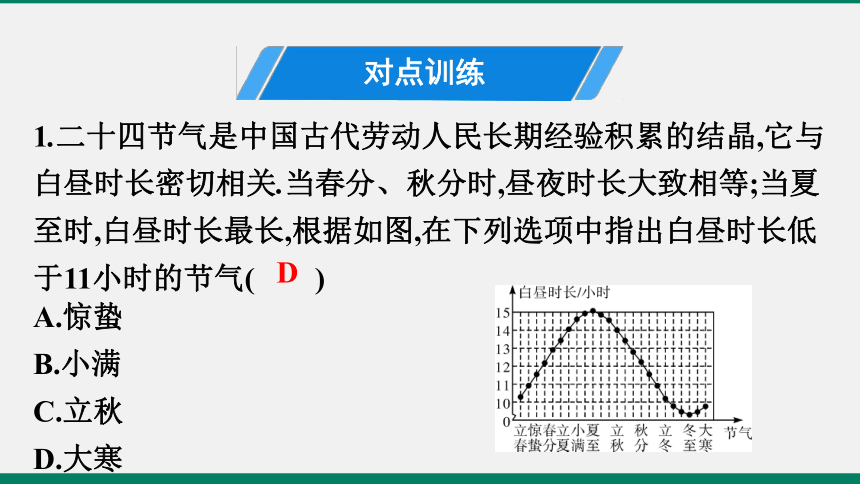
A.惊蛰
B.小满
C.立秋
D.大寒
1.二十四节气是中国古代劳动人民长期经验积累的结晶,它与白昼时长密切相关.当春分、秋分时,昼夜时长大致相等;当夏至时,白昼时长最长,根据如图,在下列选项中指出白昼时长低于11小时的节气( )
对点训练
D
2.(新题速递)(2020随州)小明从家出发步行至学校,停留一段时间后乘车返回,则下列图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是( )
B
知识点二:从图象中获取信息
理解图象上某一个点的意义,一要看横轴、纵轴分别表示哪个变量;二要看该点所在的水平方向、竖直方向的位置,这样才能得到该点的正确意义.
A.凌晨4时气温最低为-3 ℃
B.14时气温最高为8 ℃
C.从0时至14时,气温随时间增长而上升
D.从14时至24时,气温随时间增长而下降
3.如图是一台自动测温记录仪的图象,它反映了某市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
C
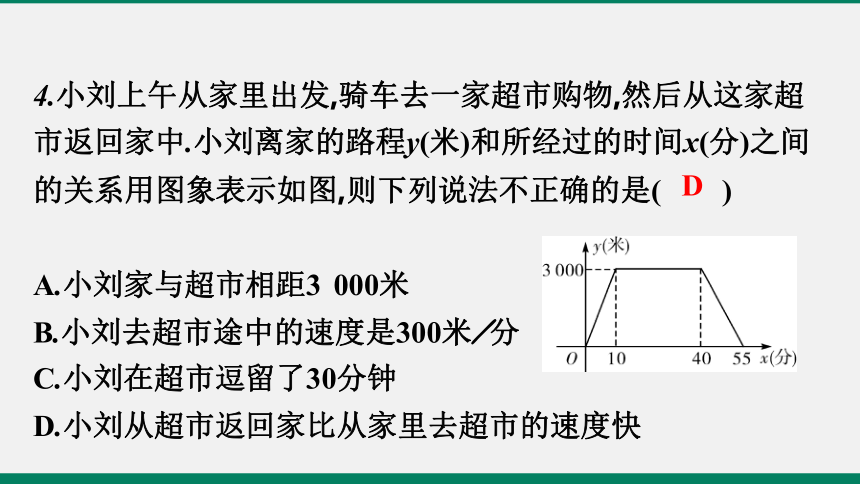
4.小刘上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.小刘离家的路程y(米)和所经过的时间x(分)之间的关系用图象表示如图,则下列说法不正确的是( )
?
A.小刘家与超市相距3 000米
B.小刘去超市途中的速度是300米/分
C.小刘在超市逗留了30分钟
D.小刘从超市返回家比从家里去超市的速度快
D
知识点三:用图象表示行程问题之间的关系
(1)用图象表示速度与时间的关系:
在如图1的速度与时间的关系图象中:
①代表物体从0开始加速运动;
②代表物体匀速运动;
③代表物体减速运动到停止.
(2)用图象表示距离与时间的关系:
在如图2的距离与时间的关系图象中:
①代表物体匀速运动;
②代表物体停止;
③代表物体反向运动直至回到原地.
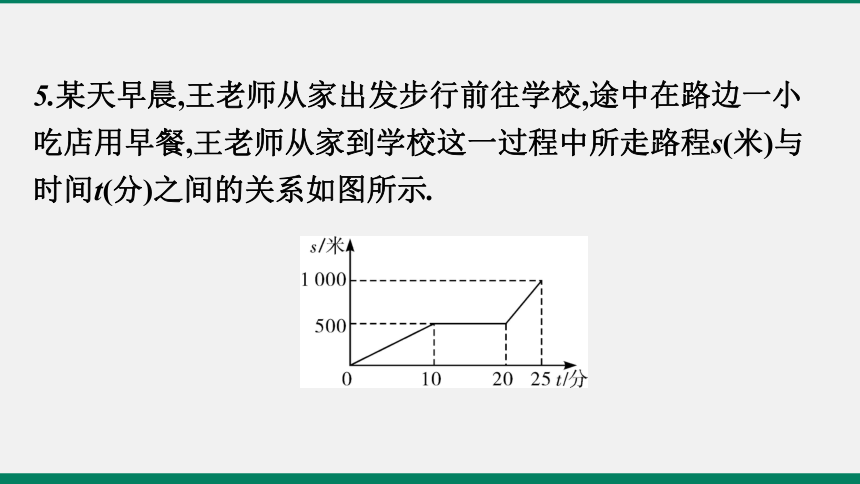
5.某天早晨,王老师从家出发步行前往学校,途中在路边一小吃店用早餐,王老师从家到学校这一过程中所走路程s(米)与时间t(分)之间的关系如图所示.
(1)他家与学校的距离为 米,从家出发到学校,王老师共用了 分钟;?
(2)王老师从家出发 分钟后开始用早餐,用早餐花了
分钟;?
10
10
25
(3)王老师用早餐前步行的速度是 米/分,?
用完早餐后步行的速度是 米/分.?
1 000
100
50
理解图象,先要理解两条数轴所表示的实际意义,
水平方向的数轴(x轴)表示自变量的变化,竖直方向的
数轴(y轴)表示因变量的变化,然后据此意义来理解实
际问题所反映的内容与图象的对应关系.此外还要注
意对图象进行水平方向左右的比较、竖直方向高低的
比较.水平方向的左右比较反映了自变量值的大小变
化,右边大于左边;竖直方向的高低比较反映了因变
量值的大小变化,高者大于低者.
小 结
精典范例
6.如图是清远市某地某一天的气温随时间变化的图象,根据图象回答:在这一天中,
(1)12时的气温是多少?
(2)什么时候气温最高,最高是多少?什么时候气温最低,最低是多少?
(3)什么时候气温大约是4 ℃?
(4)在什么时间范围内温度在上升?在什么时间范围内温度在下降?
解:(1)12时的气温是8 ℃.
(2)14时气温最高,最高气温是10 ℃;4时气温最低,最低气温是零下2 ℃.
(3)8时和20时气温大约是4 ℃.
(4)4时到14时温度在上升,0时到4时、14时到24时温度在下降.
7.(新题速递)(2020黄冈)2020年初以来,红星消毒液公司生产的消毒液在库存量为m吨的情况下,日销售量与产量持平.自1月底抗击“新冠病毒”以来,消毒液需求量猛增,该厂在生产能力不变的情况下,消毒液一度脱销,下面表示2020年初至脱销期间,该厂库存量y(吨)与时间t(天)之间的关系图象大致是( )
D
8.一天之中,海水的水深是不同的.如图是某港口从0时到12时的水深情况,结合图象回答下列问题:
(1)如图描述了哪两个变量之间的关系?其中自变量是什么?因变量是什么?
(2)大约什么时刻港口的水最深?深度约是多少?
变式练习
(3)图中A点表示的是什么?
(4)在什么时间范围内,水深在增加?什么时间范围内,水深在减少?
解:(1)描述了港口的水深和时间之间的关系,其中时间是自变量,港口的水深是因变量.
(2)3时港口的水最深,深度约是7米.
(3)图中A点表示的是6时港口的水深约是5米.
(4)从0时到3时、9时到12时水深在增加,从3时到9时水深在减少.
9.小华某天上午9时骑自行车离开家,17时回到家,他有意描绘了离家的距离与时间的变化情况,如图.
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和11时,他分别离家多远?
(3)他最初到达离家最远的地方是什么时间?离家多远?
(4)11时到13时,他行驶了多少千米?
解:(1)图象表示离家距离与时间之间的关系,时间是自变量,离家距离是因变量.
(2)15千米和20千米.
(3)13时,离家30千米.
(4)30-20=10(千米).11时到13时,他行驶了10千米.
10.假日里,小亮和爸爸骑自行车郊游,上午8时从家出发,16时返回家中,他们离家的距离与时间的关系可用图中的折线表示.
(1)他们何时到达离家最远的地方?
(2)他们何时开始第一次休息?
(3)10时到13时,他们走了多少千米?
(4)返回时,他们的平均速度是多少?
解:(1)14时.(2)10时.(3)5 千米.
(4)返回时,他们匀速运动,路程为30千米,所用时间是2小时,故平均速度为15千米/时.
11.均匀地向一个容器内注水,在注满水的过程中,水面的高度h与时间t之间的关系如图所示,则该容器是下列四个中的( )
D
★12.(创新题)如图1,在长方形ABCD中,动点P从A出发,以相同的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x,三角形PAB的面积为y,如果y与x的关系图象如图2所示,则长方形ABCD的面积为 .?
24
13.李大爷按每千克2.1元批发了一批黄瓜到镇上出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出黄瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)李大爷自带的零钱是多少?
(2)降价前他每千克黄瓜出售的价格是多少?
(3)卖了几天,黄瓜卖相不好了,随后他按每千克下降1.6元将剩余的黄瓜售完,这时他手中的钱(含备用的钱)是530元,他一共批发了多少千克的黄瓜?
(4)请问李大爷亏了还是赚了?若亏(赚)了,亏(赚)多少钱?
解:(1)由图可得李大爷自带的零钱为50元.
(2)(410-50)÷100=3.6(元).
答:降价前他每千克黄瓜出售的价格是3.6元.
(3)(530-410)÷(3.6-1.6)=60(千克),
100+60=160(千克).
答:他一共批发了160千克的黄瓜.
(4)530-160×2.1-50=144(元).
答:李大爷赚了,一共赚了144元钱.
14.〈营口改编〉如图①,在长方形ABCD中,动点E从点B出发,沿B→A→D→C方向运动至点C处停止,设点E运动的路程为x,三角形BCE的面积为y,如果y关于x的变化关系图象如图②,则当x=7时,点E应运动到( )
A.点C处
B.点D处
C.点B处
D.点A处
B
x是自变量,y是因变量,点E在运动的过程中,三角形
BCE的底边BC不变,而BC边上的高有时在变化,当点E
在AB上运动时,BC边上的高变得越来越大,此时三角形
BCE的面积不断增大;当点E在AD上运动时,BC边上的
高不变,此时三角形BCE的面积不变;当点E在DC上运
动时,BC边上的高不断减小,此时三角形BCE的面积不
断减小.观察图②,可知当x=7时,所对应的点正处于
水平线段与下降线段的交界处,即点E应运动到面积不发
生变化,若继续运动,面积随着变小的地方.结合图①,
可知点E运动到了点D处.
其特点是直观
变量之间的关系
表格法
关系式法
图象法
是从“数”的角度反
映变量之间的关系:
其特点是清楚
是从“式”的角度反
映变量之间的关系:
其特点是简单明了
是从“形”的角度反
映变量之间的关系:
总结
第3课时 用图象表示的变量间关系
学习目标
1.经历从图象中分析变量之间关系的过程,进一步体会变量之间的关系.
2.结合具体情境理解图象上的点所表示的意义.
3.能从图象中获取变量之间关系的信息,感受几何直观的作用,并能用语言进行描述.
知识要点
知识点一:用图象表示两个变量间的关系
(1)用图象表示两个变量之间关系的方法叫做图象法.
(2)如图,在利用图象表示两个变量之间的关系时,通常用水平方向的数轴(称为横轴)上的点表示自变量,用竖直方向的数轴(称为纵轴)上的点来表示因变量.过图象上的一点向横轴作垂线,其垂足表示的数据就是自变量的一个取值,然后过该点再向纵轴作垂线,其垂足表示的数就是与自变量的值对应的因变量的一个值.
A.惊蛰
B.小满
C.立秋
D.大寒
1.二十四节气是中国古代劳动人民长期经验积累的结晶,它与白昼时长密切相关.当春分、秋分时,昼夜时长大致相等;当夏至时,白昼时长最长,根据如图,在下列选项中指出白昼时长低于11小时的节气( )
对点训练
D
2.(新题速递)(2020随州)小明从家出发步行至学校,停留一段时间后乘车返回,则下列图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是( )
B
知识点二:从图象中获取信息
理解图象上某一个点的意义,一要看横轴、纵轴分别表示哪个变量;二要看该点所在的水平方向、竖直方向的位置,这样才能得到该点的正确意义.
A.凌晨4时气温最低为-3 ℃
B.14时气温最高为8 ℃
C.从0时至14时,气温随时间增长而上升
D.从14时至24时,气温随时间增长而下降
3.如图是一台自动测温记录仪的图象,它反映了某市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
C
4.小刘上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.小刘离家的路程y(米)和所经过的时间x(分)之间的关系用图象表示如图,则下列说法不正确的是( )
?
A.小刘家与超市相距3 000米
B.小刘去超市途中的速度是300米/分
C.小刘在超市逗留了30分钟
D.小刘从超市返回家比从家里去超市的速度快
D
知识点三:用图象表示行程问题之间的关系
(1)用图象表示速度与时间的关系:
在如图1的速度与时间的关系图象中:
①代表物体从0开始加速运动;
②代表物体匀速运动;
③代表物体减速运动到停止.
(2)用图象表示距离与时间的关系:
在如图2的距离与时间的关系图象中:
①代表物体匀速运动;
②代表物体停止;
③代表物体反向运动直至回到原地.
5.某天早晨,王老师从家出发步行前往学校,途中在路边一小吃店用早餐,王老师从家到学校这一过程中所走路程s(米)与时间t(分)之间的关系如图所示.
(1)他家与学校的距离为 米,从家出发到学校,王老师共用了 分钟;?
(2)王老师从家出发 分钟后开始用早餐,用早餐花了
分钟;?
10
10
25
(3)王老师用早餐前步行的速度是 米/分,?
用完早餐后步行的速度是 米/分.?
1 000
100
50
理解图象,先要理解两条数轴所表示的实际意义,
水平方向的数轴(x轴)表示自变量的变化,竖直方向的
数轴(y轴)表示因变量的变化,然后据此意义来理解实
际问题所反映的内容与图象的对应关系.此外还要注
意对图象进行水平方向左右的比较、竖直方向高低的
比较.水平方向的左右比较反映了自变量值的大小变
化,右边大于左边;竖直方向的高低比较反映了因变
量值的大小变化,高者大于低者.
小 结
精典范例
6.如图是清远市某地某一天的气温随时间变化的图象,根据图象回答:在这一天中,
(1)12时的气温是多少?
(2)什么时候气温最高,最高是多少?什么时候气温最低,最低是多少?
(3)什么时候气温大约是4 ℃?
(4)在什么时间范围内温度在上升?在什么时间范围内温度在下降?
解:(1)12时的气温是8 ℃.
(2)14时气温最高,最高气温是10 ℃;4时气温最低,最低气温是零下2 ℃.
(3)8时和20时气温大约是4 ℃.
(4)4时到14时温度在上升,0时到4时、14时到24时温度在下降.
7.(新题速递)(2020黄冈)2020年初以来,红星消毒液公司生产的消毒液在库存量为m吨的情况下,日销售量与产量持平.自1月底抗击“新冠病毒”以来,消毒液需求量猛增,该厂在生产能力不变的情况下,消毒液一度脱销,下面表示2020年初至脱销期间,该厂库存量y(吨)与时间t(天)之间的关系图象大致是( )
D
8.一天之中,海水的水深是不同的.如图是某港口从0时到12时的水深情况,结合图象回答下列问题:
(1)如图描述了哪两个变量之间的关系?其中自变量是什么?因变量是什么?
(2)大约什么时刻港口的水最深?深度约是多少?
变式练习
(3)图中A点表示的是什么?
(4)在什么时间范围内,水深在增加?什么时间范围内,水深在减少?
解:(1)描述了港口的水深和时间之间的关系,其中时间是自变量,港口的水深是因变量.
(2)3时港口的水最深,深度约是7米.
(3)图中A点表示的是6时港口的水深约是5米.
(4)从0时到3时、9时到12时水深在增加,从3时到9时水深在减少.
9.小华某天上午9时骑自行车离开家,17时回到家,他有意描绘了离家的距离与时间的变化情况,如图.
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和11时,他分别离家多远?
(3)他最初到达离家最远的地方是什么时间?离家多远?
(4)11时到13时,他行驶了多少千米?
解:(1)图象表示离家距离与时间之间的关系,时间是自变量,离家距离是因变量.
(2)15千米和20千米.
(3)13时,离家30千米.
(4)30-20=10(千米).11时到13时,他行驶了10千米.
10.假日里,小亮和爸爸骑自行车郊游,上午8时从家出发,16时返回家中,他们离家的距离与时间的关系可用图中的折线表示.
(1)他们何时到达离家最远的地方?
(2)他们何时开始第一次休息?
(3)10时到13时,他们走了多少千米?
(4)返回时,他们的平均速度是多少?
解:(1)14时.(2)10时.(3)5 千米.
(4)返回时,他们匀速运动,路程为30千米,所用时间是2小时,故平均速度为15千米/时.
11.均匀地向一个容器内注水,在注满水的过程中,水面的高度h与时间t之间的关系如图所示,则该容器是下列四个中的( )
D
★12.(创新题)如图1,在长方形ABCD中,动点P从A出发,以相同的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x,三角形PAB的面积为y,如果y与x的关系图象如图2所示,则长方形ABCD的面积为 .?
24
13.李大爷按每千克2.1元批发了一批黄瓜到镇上出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出黄瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)李大爷自带的零钱是多少?
(2)降价前他每千克黄瓜出售的价格是多少?
(3)卖了几天,黄瓜卖相不好了,随后他按每千克下降1.6元将剩余的黄瓜售完,这时他手中的钱(含备用的钱)是530元,他一共批发了多少千克的黄瓜?
(4)请问李大爷亏了还是赚了?若亏(赚)了,亏(赚)多少钱?
解:(1)由图可得李大爷自带的零钱为50元.
(2)(410-50)÷100=3.6(元).
答:降价前他每千克黄瓜出售的价格是3.6元.
(3)(530-410)÷(3.6-1.6)=60(千克),
100+60=160(千克).
答:他一共批发了160千克的黄瓜.
(4)530-160×2.1-50=144(元).
答:李大爷赚了,一共赚了144元钱.
14.〈营口改编〉如图①,在长方形ABCD中,动点E从点B出发,沿B→A→D→C方向运动至点C处停止,设点E运动的路程为x,三角形BCE的面积为y,如果y关于x的变化关系图象如图②,则当x=7时,点E应运动到( )
A.点C处
B.点D处
C.点B处
D.点A处
B
x是自变量,y是因变量,点E在运动的过程中,三角形
BCE的底边BC不变,而BC边上的高有时在变化,当点E
在AB上运动时,BC边上的高变得越来越大,此时三角形
BCE的面积不断增大;当点E在AD上运动时,BC边上的
高不变,此时三角形BCE的面积不变;当点E在DC上运
动时,BC边上的高不断减小,此时三角形BCE的面积不
断减小.观察图②,可知当x=7时,所对应的点正处于
水平线段与下降线段的交界处,即点E应运动到面积不发
生变化,若继续运动,面积随着变小的地方.结合图①,
可知点E运动到了点D处.
其特点是直观
变量之间的关系
表格法
关系式法
图象法
是从“数”的角度反
映变量之间的关系:
其特点是清楚
是从“式”的角度反
映变量之间的关系:
其特点是简单明了
是从“形”的角度反
映变量之间的关系:
总结
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
