2020——2021学年北师大版七年级数学下册 1.5 .1平方差公式课件(共20张)
文档属性
| 名称 | 2020——2021学年北师大版七年级数学下册 1.5 .1平方差公式课件(共20张) |  | |
| 格式 | pptx | ||
| 文件大小 | 182.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 22:58:37 | ||
图片预览








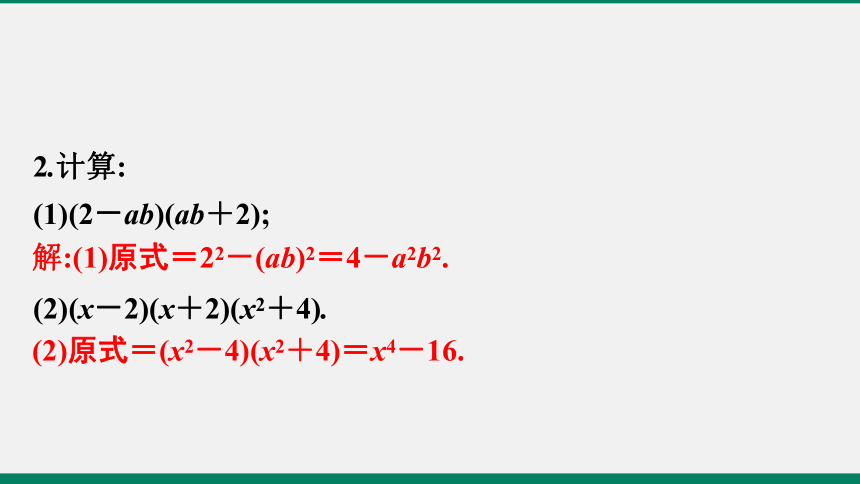
文档简介
第一章 整式的乘除
第1课时 平方差公式
学习目标
1.经历探索平方差公式的过程,进一步发展学生的符号意识和推理能力.
2.(课标)会推导平方差公式,并能利用公式进行简单的计算.
知识点一:平方差公式
(1)平方差公式:(a+b)(a-b)=a2-b2,
即两数和与这两数差的 ,等于它们的 .?
(2)平方差公式的推导(代数方法):
平方差
知识要点
积
a2-ab+ab-b2=a2-b2.
(3)公式结构记忆口诀:
两项和乘两项差,符号相反切记牢;
结果就是平方差,基本形式要牢记;
公式运用可推广,两式类比两数法.
1.计算:
(1)(x+1)(x-1); (2)(1+2a)(1-2a);
(2)原式=1-(2a)2=1-4a2.
对点训练
解:(1)原式=x2-1.
(3)(x+3y)(x-3y); (4)(3y+2z)(3y-2z).
(4)原式=(3y)2-(2z)2=9y2-4z2.
(3)原式=x2-(3y)2=x2-9y2.
知识点二:平方差公式的常见变形
(1)位置变化:
(b+a)(-b+a)=(a+b)(a-b)=a2-b2.
(2)符号变化:
(-a-b)(-a+b)=(-a)2-b2=a2-b2.
(3)系数变化:
(3a+2b)(3a-2b)=(3a)2-(2b)2=9a2-4b2.
(4)指数变化:
(a2+b2)(a2-b2)=(a2)2-(b2)2=a4-b4.
(5)连用公式变化:
(a+b)(a-b)(a2+b2)=(a2-b2)(a2+b2)=a4-b4.
2.计算:
(1)(2-ab)(ab+2);
(2)(x-2)(x+2)(x2+4).
(2)原式=(x2-4)(x2+4)=x4-16.
解:(1)原式=22-(ab)2=4-a2b2.
知识点三:巧用平方差公式计算
当出现多个因式相乘时,要仔细观察式子的特点,看是不是符合平方差公式的结构特征或根据题意“凑”出符合平方差公式结构的形式,然后依次运用公式,一直到不能运用为止.
(2)巧用公式计算:18×20-192.
(2)原式=(19-1)(19+1)-192=192-1-192=-1.
解:(1)原式=m2-4-m2=-4.
4.计算(3a+b)(3a-b)的结果等于( )
A.9a2+b2 B.3a2-b2
C.9a2-b2 D.3a2+b2
精典范例
C
5.下列各式中,能用平方差公式计算的是( )
变式练习
C
(3)(a+3b)(a-3b); (4)(x2+y)(x2-y).
(4)原式=(x2)2-y2=x4-y2.
6.计算:
(1)(2+x)(2-x); (2)(m-3)(m+3);
(3)原式=a2-(3b)2=a2-9b2.
(2)原式=m2-9.
解:(1)原式=4-x2.
7.计算:
(1)(a+4)(a-4); (2)(4-x)(4+x);
(3)(4x+2y)(4x-2y); (4)(2m2+n)(2m2-n).
?
(4)原式=(2m2)2-n2=4m4-n2.
(3)原式=(4x)2-(2y)2=16x2-4y2.
(2)原式=16-x2.
解:(1)原式=a2-16.
7.运用平方差公式计算:
(1)(-m-n)(-m+n);
(2)(2+m)(-2+m).
(2)原式=(m+2)(m-2)=m2-4.
解:(1)原式=(-m)2-n2=m2-n2.
(2)(y+2x)(2x-y).
(2)原式=(2x+y)(2x-y)=(2x)2-y2=4x2-y2.
(新题速递)(2020淮安)如果一个数等于两个连续奇数的平方差,那么我们称这个数为“幸福数”.下列数中为“幸福数”的是( )
A.205
B.250
C.502
D.520
D
9.计算:(3a-b)(3a+b)-(a2+b2).
解:原式=9a2-b2-a2-b2=8a2-2b2.
★10.计算:(x+2y)(x-2y)(x2+4y2).
解:原式=(x2-4y2)(x2+4y2)=x4-16y4.
第1课时 平方差公式
学习目标
1.经历探索平方差公式的过程,进一步发展学生的符号意识和推理能力.
2.(课标)会推导平方差公式,并能利用公式进行简单的计算.
知识点一:平方差公式
(1)平方差公式:(a+b)(a-b)=a2-b2,
即两数和与这两数差的 ,等于它们的 .?
(2)平方差公式的推导(代数方法):
平方差
知识要点
积
a2-ab+ab-b2=a2-b2.
(3)公式结构记忆口诀:
两项和乘两项差,符号相反切记牢;
结果就是平方差,基本形式要牢记;
公式运用可推广,两式类比两数法.
1.计算:
(1)(x+1)(x-1); (2)(1+2a)(1-2a);
(2)原式=1-(2a)2=1-4a2.
对点训练
解:(1)原式=x2-1.
(3)(x+3y)(x-3y); (4)(3y+2z)(3y-2z).
(4)原式=(3y)2-(2z)2=9y2-4z2.
(3)原式=x2-(3y)2=x2-9y2.
知识点二:平方差公式的常见变形
(1)位置变化:
(b+a)(-b+a)=(a+b)(a-b)=a2-b2.
(2)符号变化:
(-a-b)(-a+b)=(-a)2-b2=a2-b2.
(3)系数变化:
(3a+2b)(3a-2b)=(3a)2-(2b)2=9a2-4b2.
(4)指数变化:
(a2+b2)(a2-b2)=(a2)2-(b2)2=a4-b4.
(5)连用公式变化:
(a+b)(a-b)(a2+b2)=(a2-b2)(a2+b2)=a4-b4.
2.计算:
(1)(2-ab)(ab+2);
(2)(x-2)(x+2)(x2+4).
(2)原式=(x2-4)(x2+4)=x4-16.
解:(1)原式=22-(ab)2=4-a2b2.
知识点三:巧用平方差公式计算
当出现多个因式相乘时,要仔细观察式子的特点,看是不是符合平方差公式的结构特征或根据题意“凑”出符合平方差公式结构的形式,然后依次运用公式,一直到不能运用为止.
(2)巧用公式计算:18×20-192.
(2)原式=(19-1)(19+1)-192=192-1-192=-1.
解:(1)原式=m2-4-m2=-4.
4.计算(3a+b)(3a-b)的结果等于( )
A.9a2+b2 B.3a2-b2
C.9a2-b2 D.3a2+b2
精典范例
C
5.下列各式中,能用平方差公式计算的是( )
变式练习
C
(3)(a+3b)(a-3b); (4)(x2+y)(x2-y).
(4)原式=(x2)2-y2=x4-y2.
6.计算:
(1)(2+x)(2-x); (2)(m-3)(m+3);
(3)原式=a2-(3b)2=a2-9b2.
(2)原式=m2-9.
解:(1)原式=4-x2.
7.计算:
(1)(a+4)(a-4); (2)(4-x)(4+x);
(3)(4x+2y)(4x-2y); (4)(2m2+n)(2m2-n).
?
(4)原式=(2m2)2-n2=4m4-n2.
(3)原式=(4x)2-(2y)2=16x2-4y2.
(2)原式=16-x2.
解:(1)原式=a2-16.
7.运用平方差公式计算:
(1)(-m-n)(-m+n);
(2)(2+m)(-2+m).
(2)原式=(m+2)(m-2)=m2-4.
解:(1)原式=(-m)2-n2=m2-n2.
(2)(y+2x)(2x-y).
(2)原式=(2x+y)(2x-y)=(2x)2-y2=4x2-y2.
(新题速递)(2020淮安)如果一个数等于两个连续奇数的平方差,那么我们称这个数为“幸福数”.下列数中为“幸福数”的是( )
A.205
B.250
C.502
D.520
D
9.计算:(3a-b)(3a+b)-(a2+b2).
解:原式=9a2-b2-a2-b2=8a2-2b2.
★10.计算:(x+2y)(x-2y)(x2+4y2).
解:原式=(x2-4y2)(x2+4y2)=x4-16y4.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
