8.2 幂的乘方与积的乘方(第2课时)(共29张PPT)
文档属性
| 名称 | 8.2 幂的乘方与积的乘方(第2课时)(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 00:00:00 | ||
图片预览








文档简介
第1课时
8.2 幂的乘方与积的乘方
第8章 幂的运算
2020-2021学年度苏科版七年级下册
问题
如果甲球的半径是乙球的n倍,那么甲球的体积是乙球的 倍.
新课导入
地球、木星、太阳可以近似地看作是球体,木星、太阳的半径分别约是地球的10倍和 倍,它们的体积分别约是地球的多少倍?
木星、太阳的体积大约是地球的 和 倍.
(根据幂的性质 )
( )
根据同底数幂的乘法的性质
探究新知
做一做
计算下列各式,并说明理由.
(1)
(2)
(3)
(4)
(m,n都是正整数).
幂的乘方,底数 ,指数 .
不变
相乘
结论
例1 计算:
(m是正整数);
(n是正整数).
解:
例题讲解
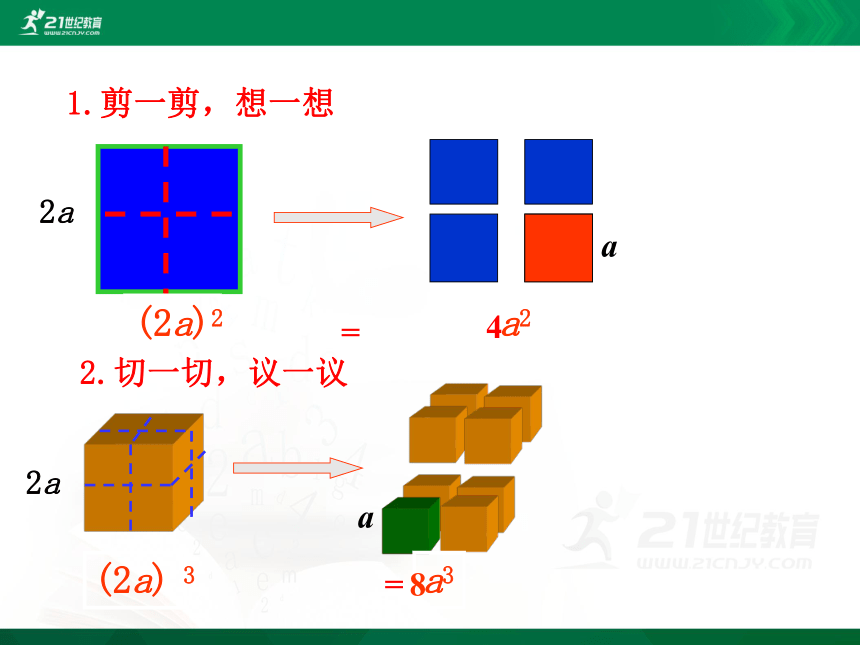
1.剪一剪,想一想
2.切一切,议一议
2a
(2a)2
a2
a
a3
(2a) 3
2a
a
4
=
8
=
同理:
(乘方的意义)
(乘法交换律、结合律)
(同底数幂相乘的法则)
(1)
(2)
观察、猜想
例2 计算:
解:
例题讲解
积的乘方
(ab)n =?
思考:
猜想: (ab)n = (当m、n都是正整数)
即:
(乘方的意义)
(乘法结合律)
(乘方的意义)
an·bn
(ab)n = ab·ab·……·ab
=(a·a·……·a) (b·b·……·b)
=an·bn
n个ab
n个a
n个b
(ab)n = (n都是正整数)
an·bn
语言叙述:积的乘方,等于把积的每一因式分别乘方,再把所得的幂相乘.
例3 计算:
(1) (5m)3 ; (2) (-xy2)3.
解: (1) (5m)3=53?m3 = 125m3;
(2) (-xy2)3=(-x)3?(y2)3=-x3y6.
例题讲解
公 式 的 拓 展
(abc)n=an·bn·cn
(abc)n=[(ab)·c]n
=(ab)n·cn
= an·bn·cn.
=(-2)4x4y4
(-2xy)4
=16x4y4
公式的反向使用
(ab)n = an·bn
(m,n都是正整数)
反向使用:
an·bn = (ab)n
试用简便方法计算:
(1) 23×53
(2) 28×58
= (2×5)3
= 103.
= (2×5)8
= 108.
(3) (-5)15 × (-2)15
(4) 24 × 44 ×(-0.125)4
= (-5)×[(-5)×(-2)]15
= -5×1015 .
= [2×4×(-0.125)]4
= 14
= 1 .
思考
例4 计算:
解:
例题讲解
例5 球的体积计算公式为 (其中V、r分别表示球的体积和半径).木星可以近似地看成球体,半径约为7.15×104km,求木星的体积.
解:
答:木星的体积大约是1.53×1015km3.
1.计算:
1.计算:
2.下面的计算是否正确?如有错误,请改正.
不对
改正
不对
改正
3.计算:
(1)(m4)2+m5·m3; (2)(x5)4+(x10)2;
(3)(a3)5·(a2)2; (4)210·410.
=m8+x8
=2m8;
=210·220
=230.
=a15·a4
=a19;
=x20+x20
=2x20;
4.一个正方体的棱长是102cm,它的体积是多少?
解:体积是(102)3=106cm3=1m3.
5.填空:
(1)82=2( )=22×2( );
(2)a12=(a3)( )=(a2)( )=a3·a( ).
6
4
4
9
6
1.计算:
2.下面的计算是否正确?如有错误,请改正.
不对
改正
不对
改正
3.计算:
(1) a5·a3+(2a2)4; (2)-2x6-(-3x2)3.
=a8+16a8
=17a8;
=-2x6+27x6
=25x6.
4.如图,圆柱体储油罐的半径是20m、高是40m(不计壁厚),求它的容积.如果该储油罐最大储油高度为30m,最多能储油多少(单位:L)?
解:容积是3.14× 202×40=50240m3=5.024×107L.
最多储油量为:3.14× 202×30=37680m3=3.768×107L.
谢谢聆听
8.2 幂的乘方与积的乘方
第8章 幂的运算
2020-2021学年度苏科版七年级下册
问题
如果甲球的半径是乙球的n倍,那么甲球的体积是乙球的 倍.
新课导入
地球、木星、太阳可以近似地看作是球体,木星、太阳的半径分别约是地球的10倍和 倍,它们的体积分别约是地球的多少倍?
木星、太阳的体积大约是地球的 和 倍.
(根据幂的性质 )
( )
根据同底数幂的乘法的性质
探究新知
做一做
计算下列各式,并说明理由.
(1)
(2)
(3)
(4)
(m,n都是正整数).
幂的乘方,底数 ,指数 .
不变
相乘
结论
例1 计算:
(m是正整数);
(n是正整数).
解:
例题讲解
1.剪一剪,想一想
2.切一切,议一议
2a
(2a)2
a2
a
a3
(2a) 3
2a
a
4
=
8
=
同理:
(乘方的意义)
(乘法交换律、结合律)
(同底数幂相乘的法则)
(1)
(2)
观察、猜想
例2 计算:
解:
例题讲解
积的乘方
(ab)n =?
思考:
猜想: (ab)n = (当m、n都是正整数)
即:
(乘方的意义)
(乘法结合律)
(乘方的意义)
an·bn
(ab)n = ab·ab·……·ab
=(a·a·……·a) (b·b·……·b)
=an·bn
n个ab
n个a
n个b
(ab)n = (n都是正整数)
an·bn
语言叙述:积的乘方,等于把积的每一因式分别乘方,再把所得的幂相乘.
例3 计算:
(1) (5m)3 ; (2) (-xy2)3.
解: (1) (5m)3=53?m3 = 125m3;
(2) (-xy2)3=(-x)3?(y2)3=-x3y6.
例题讲解
公 式 的 拓 展
(abc)n=an·bn·cn
(abc)n=[(ab)·c]n
=(ab)n·cn
= an·bn·cn.
=(-2)4x4y4
(-2xy)4
=16x4y4
公式的反向使用
(ab)n = an·bn
(m,n都是正整数)
反向使用:
an·bn = (ab)n
试用简便方法计算:
(1) 23×53
(2) 28×58
= (2×5)3
= 103.
= (2×5)8
= 108.
(3) (-5)15 × (-2)15
(4) 24 × 44 ×(-0.125)4
= (-5)×[(-5)×(-2)]15
= -5×1015 .
= [2×4×(-0.125)]4
= 14
= 1 .
思考
例4 计算:
解:
例题讲解
例5 球的体积计算公式为 (其中V、r分别表示球的体积和半径).木星可以近似地看成球体,半径约为7.15×104km,求木星的体积.
解:
答:木星的体积大约是1.53×1015km3.
1.计算:
1.计算:
2.下面的计算是否正确?如有错误,请改正.
不对
改正
不对
改正
3.计算:
(1)(m4)2+m5·m3; (2)(x5)4+(x10)2;
(3)(a3)5·(a2)2; (4)210·410.
=m8+x8
=2m8;
=210·220
=230.
=a15·a4
=a19;
=x20+x20
=2x20;
4.一个正方体的棱长是102cm,它的体积是多少?
解:体积是(102)3=106cm3=1m3.
5.填空:
(1)82=2( )=22×2( );
(2)a12=(a3)( )=(a2)( )=a3·a( ).
6
4
4
9
6
1.计算:
2.下面的计算是否正确?如有错误,请改正.
不对
改正
不对
改正
3.计算:
(1) a5·a3+(2a2)4; (2)-2x6-(-3x2)3.
=a8+16a8
=17a8;
=-2x6+27x6
=25x6.
4.如图,圆柱体储油罐的半径是20m、高是40m(不计壁厚),求它的容积.如果该储油罐最大储油高度为30m,最多能储油多少(单位:L)?
解:容积是3.14× 202×40=50240m3=5.024×107L.
最多储油量为:3.14× 202×30=37680m3=3.768×107L.
谢谢聆听
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
