8.1 同底数幂的乘法(第1课时)(共26张PPT)
文档属性
| 名称 | 8.1 同底数幂的乘法(第1课时)(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 21:09:54 | ||
图片预览







文档简介
第1课时
8.1 同底数幂的乘法
第8章 幂的运算
2020-2021学年度苏科版七年级下册
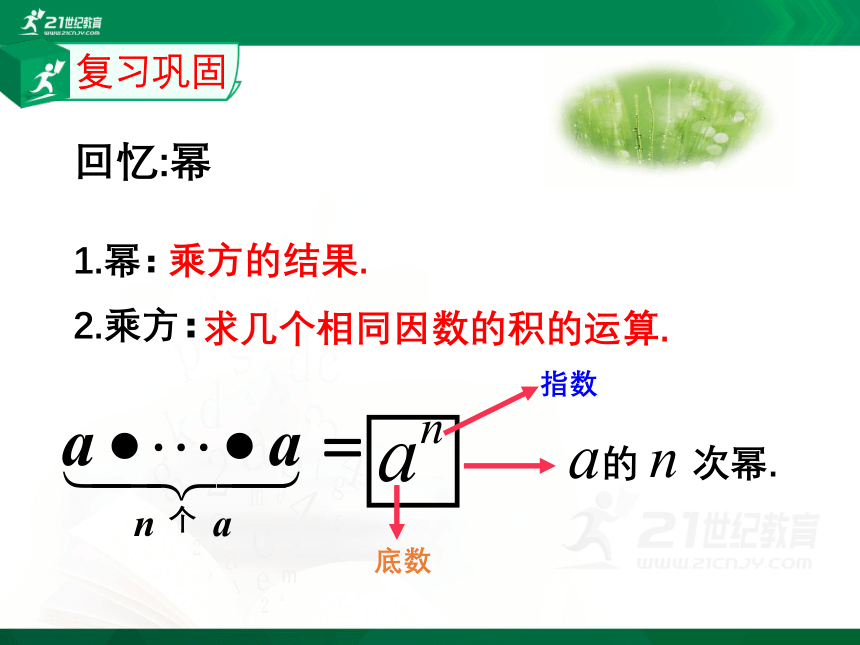
1.幂:
乘方的结果.
个
回忆:幂
底数
指数
的 次幂.
求几个相同因数的积的运算.
2.乘方:
复习巩固
个
个
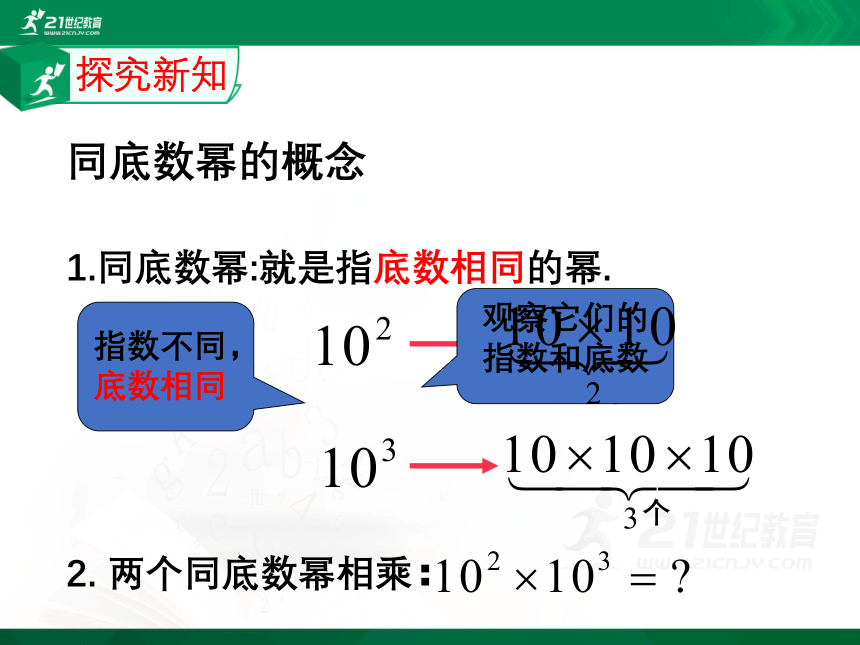
1.同底数幂:就是指底数相同的幂.
2. 两个同底数幂相乘:
指数不同,底数相同
同底数幂的概念
观察它们的指数和底数
探究新知
两个同底数幂相乘:
(乘方的意义)
(乘法结合律)
(乘方的意义)
探索:同底数幂的乘法法则
解:
探究新知
继续探索:
将上题中的底数10改为任意底数 ,则有
即,
个
个
个
即,
如果我把上题中的指数 3,2改成一般的任意正整数并分别用字母 来表示.
同底数幂的乘法法则:
( 都是正整数)
即,同底数幂相乘,底数_____,指数______.
不变
相加
(1)等号左边是什么运算?
法则剖析:
( 都是正整数)
(2)等号左右两边的指数有什么关系?
答:等号左边是乘法运算 .
答: 等号右边的指数是等号左边的两个指数相加的和.
公式推广:
当三个或三个以上的同底数幂相乘时,法则可以推广为:
( 都是正整数)
即,当幂与幂之间相乘时,只要是底数相同,就可以直接利用同底数幂的乘法法则:底数不变,指数相加.
计算下列各式,结果用幂的形式表示.
解
例1 计算:
解
(m是正整数);
例题讲解
我国“天河-1A”超级计算机的实测运算速度达到每秒2.566千万亿次.如果按这个速度工作一整天,那么它能运算多少次?
解 2.566千万亿次=2.566×107×108次,24小时=24×3.6×103秒.
由乘法的交换律和结合律,得
(2.566×107×108) × (24×3.6×103)
=(2.566×24×3.6) ×(107×108×103)
=221.7024×1018≈2.2×1020(次).
答:它一天约能运算2.2×1020次.
例2 一颗卫星绕地球运行的速度是7.9×103m/s,求这颗卫星运行1h的路程.
解:因为1h=3.6×103s,所以这颗卫星运行1h的路程为:
(7.9×103)×(3.6×103)
=(7.9×3.6)×(103×103)
=2.844×107(m).
答:这颗卫星运行1h的路程是2.844×107m.
计算下列各式,结果用幂的形式表示.
解
1、 把下列各式表示成幂的形式:
解:原式=
解:原式=
解:原式=
解:原式=
2、 太阳系的形状像一个以太阳为中心的大圆盘,光通过这个圆盘半径的时间约为2×104s.光的速度约为3×105km/s.求太阳系的直径.
解:2×3×105×2×104
==12×109(km).
答:太阳系的直径约为12×l09km.
1.判断正误:
×
×
×
×
随堂练习
点评:区分是乘法还是加法运算,再选择不同的法则.
2.填空:
若
则
点拨:同底数幂乘法公式的逆用也很重要.
3.计算:
已知:
求
解:
光在真空中的速度大约是3×108 千米/秒,太阳系以外距离地球最近的恒星是比邻星,它发出的光到达地球大约需要4.22年.
一年以3×107 s计算,比邻星与地球的距离约为多少千米?
等于多少呢?
幂的意义
幂的意义
(根据 )
(根据 )
乘法结合律
下面的计算对不对?如果不对,应该怎样改正?
不对
改正
不对
改正
不对
改正
不对
改正
计算:
注意事项:
1.同底数幂相乘,底数不变,指数相加.对这个法则要注重理解“同底,相乘,不变,相加”这八个字.
2.底数可以是一个数,也可以是单项式或多项式.运算时不同底的要先化为同底的,才可以运用法则.
4.解题时,要注意指数为1的情况,不要漏掉.
3.解题时,底数是负数的要用括号把底数括起来.
谢谢聆听
8.1 同底数幂的乘法
第8章 幂的运算
2020-2021学年度苏科版七年级下册
1.幂:
乘方的结果.
个
回忆:幂
底数
指数
的 次幂.
求几个相同因数的积的运算.
2.乘方:
复习巩固
个
个
1.同底数幂:就是指底数相同的幂.
2. 两个同底数幂相乘:
指数不同,底数相同
同底数幂的概念
观察它们的指数和底数
探究新知
两个同底数幂相乘:
(乘方的意义)
(乘法结合律)
(乘方的意义)
探索:同底数幂的乘法法则
解:
探究新知
继续探索:
将上题中的底数10改为任意底数 ,则有
即,
个
个
个
即,
如果我把上题中的指数 3,2改成一般的任意正整数并分别用字母 来表示.
同底数幂的乘法法则:
( 都是正整数)
即,同底数幂相乘,底数_____,指数______.
不变
相加
(1)等号左边是什么运算?
法则剖析:
( 都是正整数)
(2)等号左右两边的指数有什么关系?
答:等号左边是乘法运算 .
答: 等号右边的指数是等号左边的两个指数相加的和.
公式推广:
当三个或三个以上的同底数幂相乘时,法则可以推广为:
( 都是正整数)
即,当幂与幂之间相乘时,只要是底数相同,就可以直接利用同底数幂的乘法法则:底数不变,指数相加.
计算下列各式,结果用幂的形式表示.
解
例1 计算:
解
(m是正整数);
例题讲解
我国“天河-1A”超级计算机的实测运算速度达到每秒2.566千万亿次.如果按这个速度工作一整天,那么它能运算多少次?
解 2.566千万亿次=2.566×107×108次,24小时=24×3.6×103秒.
由乘法的交换律和结合律,得
(2.566×107×108) × (24×3.6×103)
=(2.566×24×3.6) ×(107×108×103)
=221.7024×1018≈2.2×1020(次).
答:它一天约能运算2.2×1020次.
例2 一颗卫星绕地球运行的速度是7.9×103m/s,求这颗卫星运行1h的路程.
解:因为1h=3.6×103s,所以这颗卫星运行1h的路程为:
(7.9×103)×(3.6×103)
=(7.9×3.6)×(103×103)
=2.844×107(m).
答:这颗卫星运行1h的路程是2.844×107m.
计算下列各式,结果用幂的形式表示.
解
1、 把下列各式表示成幂的形式:
解:原式=
解:原式=
解:原式=
解:原式=
2、 太阳系的形状像一个以太阳为中心的大圆盘,光通过这个圆盘半径的时间约为2×104s.光的速度约为3×105km/s.求太阳系的直径.
解:2×3×105×2×104
==12×109(km).
答:太阳系的直径约为12×l09km.
1.判断正误:
×
×
×
×
随堂练习
点评:区分是乘法还是加法运算,再选择不同的法则.
2.填空:
若
则
点拨:同底数幂乘法公式的逆用也很重要.
3.计算:
已知:
求
解:
光在真空中的速度大约是3×108 千米/秒,太阳系以外距离地球最近的恒星是比邻星,它发出的光到达地球大约需要4.22年.
一年以3×107 s计算,比邻星与地球的距离约为多少千米?
等于多少呢?
幂的意义
幂的意义
(根据 )
(根据 )
乘法结合律
下面的计算对不对?如果不对,应该怎样改正?
不对
改正
不对
改正
不对
改正
不对
改正
计算:
注意事项:
1.同底数幂相乘,底数不变,指数相加.对这个法则要注重理解“同底,相乘,不变,相加”这八个字.
2.底数可以是一个数,也可以是单项式或多项式.运算时不同底的要先化为同底的,才可以运用法则.
4.解题时,要注意指数为1的情况,不要漏掉.
3.解题时,底数是负数的要用括号把底数括起来.
谢谢聆听
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
