9.4 乘法公式(第1课时)(共32张PPT)
文档属性
| 名称 | 9.4 乘法公式(第1课时)(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 00:00:00 | ||
图片预览










文档简介
9.4 乘法公式
第9章 整式乘法与因式分解
第1课时
2020-2021学年度苏科版七年级下册
去年,一位农民在一次“科技下乡”活动中得到启示,将一块边长为a米的正方形农田改成试验田,种上了优质的杂交水稻,一年来,收益很大,今年,又一次“科技下乡”活动,使老农铁了心,要走科技兴农的路子,于是他想把原来的试验田,边长增加b米,形成四块试验田,种植不同的新品种.
问题1:同学们,谁来帮老爷爷实现这个愿望呢?
新课导入
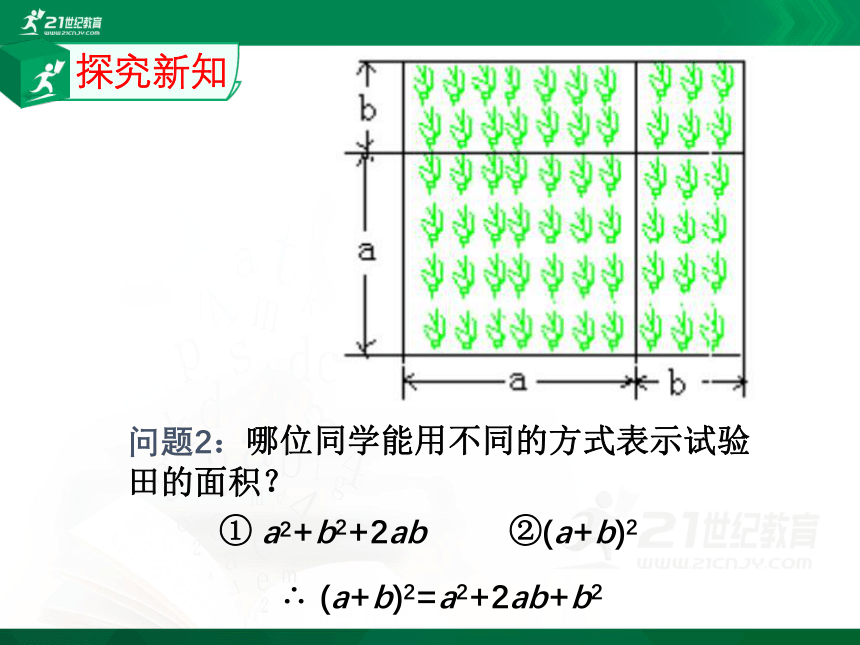
问题2:哪位同学能用不同的方式表示试验田的面积?
① a2+b2+2ab ②(a+b)2
∴ (a+b)2=a2+2ab+b2
探究新知
问题3:哪位同学能从代表运算角度推导出这样 的公式?
想一想: (a-b)2等于什么?你是怎样想的?
问题4:上面的几何解释和代数推导各有什么利弊?
几何解释:优点:直观、易懂、明了
缺点:有局限性、受条件限制
代数推导:优点:应用宽、广
缺点:不直观、抽象
例1 计算:(a-b)2 .
解:
例题讲解
问题5:你能用数学语言描述出完全平方公式I和II吗?
两个数的和(或差)的平方等于这两个数的平方和与它们积的2倍的和(或差).
完全平方公式 逆向完全平方公式
I.(a+b)2=a2+2ab+b2 a2+2ab+b2=(a+b)2
II. (a-b)2 =[a+(-b)]2 a2-2ab+b2 =[a+(-b)]2
=a2-2ab+b2 = (a-b)2
例2 用完全平方式计算:
解:
计算下列各题,你能发现什么规律?
(1) (x+1)(x-1);
(2) (m+2)(m-2);
(3) (2x+1)(2x-1) ;
答案:
(x+1)(x-1)=_________;
(2) (m+2)(m-2)=__________;
(3) (2x+1)(2x-1)=________.
x2-1
m2-4
4x2-1
合作交流,探究新知
探究:
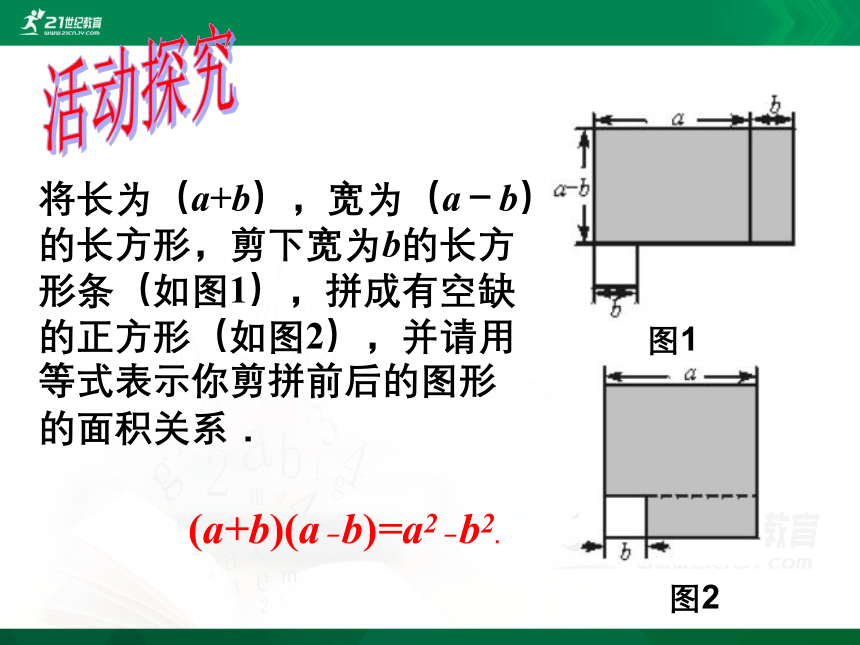
将长为(a+b),宽为(a-b)的长方形,剪下宽为b的长方形条(如图1),拼成有空缺的正方形(如图2),并请用等式表示你剪拼前后的图形的面积关系.?
(a+b)(a-b)=a2-b2.
图1
图2
活动探究
平方差公式:
(a+b)(a- b) =
a2- b2.
即两数和与这两数差的积等于这两个数的平方差.
(a+b)(a- b)=
a2- b2 .
a2- ab+ab- b2=
注:这里的两数可以是数字、字母、单项式也可以是两个多项式等.
例3 用平方差公式计算:
解:
运用平方差公式计算:
(1) (3x+2) (3x-2);
(2) (b+2a)(2a-b);
(3) (-x+2y) (-x-2y).
分析:在(1)中,可以把3x看成a,2看成b,即
(3x +2) ( 3x -2) = (3x)2 -22
(a + b) ( a - b) = a2 - b2
下列计算对不对?如果不对,怎样改正?
2)
错
1)
错
例4 计算:
解:
例5 计算:
解:
例6 计算:
解:
例7 计算:
解:
应用
1、直接应用
例1:利用完全平方公式计算.
(1) (2x+3)2 (2) (mn-a)2
2、灵活应用
例2:利用完全平方公式计算.
(-x+2y)2 (2)(-x-y)2
(3)(x+y-z)2 (4)(x+y)2-(x-y)2
3、简便算法
例3:计算.
(1) 1022 (2) 1972
活动与探究
1.已知x+y=8 xy=12 求x2+y2的值.
2.已知x2-2x+y2+6y+10=0 求x+y的值.
3.已知 a=2002x+2001 b=2002x+2002
c=2002x+2003
求a2+b2+c2-ab-bc-ac的值.
趣味题
一位老人非常喜欢孩子,每当有孩子到他家做客时,老人都拿出糖果招待他们,来一个孩子,老人就给这个孩子一块糖,来两个孩子,老人就给每个孩子两块糖……
1、第一天有a个男孩去了老人家,老人一共给了这些孩子多少块糖?
2、第二天有b个女孩去了老人家,老人一共给了这些孩子多少块糖?
3、第三天有(a+b)个孩子一块去看老人家,老人一共给了这些孩子多少块糖?
4、这些孩子第三天得到糖果数与前两天他们得到的糖果总数哪个多?多多少?为什么?
习题包
A:(3x-1)2=(3x)2-2(3x)( )+( )2
=9x2-6x+1.
B: (x+2)2=x2-kx+4 那么 k的值是( ).
A.-2 B.2 C.-4 D.4
C:不论x为何值(x+a)2=x2+x+a2则常数a等于( ).
A.2 B.-2 C.1/2 D.-1/2
D:若m2+km+36是一个完全平方式,则常数k=_________.
简便计算:
(1) 102×98;
(2) (y+2) (y-2) – (y-1) (y+5) .
解: (1)102×98
=(100+2)(100-2)
= 1002-22
=10000–4
= 9996.
(y+2)(y-2)-(y-1)(y+5)
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= -4y+1.
利用平方差公式计算:
(1)(a+3b)(a-3b);
(2)(3+2a)(-3+2a).
(3)51×49
(4)(x+y-1)(x+y+1)
快乐练习:
看谁做得最快最正确!
计算下列各题
轻松闯关:
1002×998 (转化思想)
(x+y)(x-y)(x2+y2) (灵活运用)
(3) (a+b)2-(a-b)2 (逆向思维训练)
运用完全平方公式计算:
解:
1.下面各式的计算错在哪里?应当怎样计算?
没有加乘积的2倍项,应改为:
没有减乘积的2倍项,平方项应该是加的,应改为:
2,计算下列各题:
平方差公式
这是两个特殊的多项式相乘.
两个数的和与这两个数差的积,等于它们的平方差.
3.运用乘法公式计算:
思维延伸
已知,两个正方形的周长之和等于32cm,它们的面积之差为48cm2,求这两个正方形的边长.
超越自我
谢谢聆听
第9章 整式乘法与因式分解
第1课时
2020-2021学年度苏科版七年级下册
去年,一位农民在一次“科技下乡”活动中得到启示,将一块边长为a米的正方形农田改成试验田,种上了优质的杂交水稻,一年来,收益很大,今年,又一次“科技下乡”活动,使老农铁了心,要走科技兴农的路子,于是他想把原来的试验田,边长增加b米,形成四块试验田,种植不同的新品种.
问题1:同学们,谁来帮老爷爷实现这个愿望呢?
新课导入
问题2:哪位同学能用不同的方式表示试验田的面积?
① a2+b2+2ab ②(a+b)2
∴ (a+b)2=a2+2ab+b2
探究新知
问题3:哪位同学能从代表运算角度推导出这样 的公式?
想一想: (a-b)2等于什么?你是怎样想的?
问题4:上面的几何解释和代数推导各有什么利弊?
几何解释:优点:直观、易懂、明了
缺点:有局限性、受条件限制
代数推导:优点:应用宽、广
缺点:不直观、抽象
例1 计算:(a-b)2 .
解:
例题讲解
问题5:你能用数学语言描述出完全平方公式I和II吗?
两个数的和(或差)的平方等于这两个数的平方和与它们积的2倍的和(或差).
完全平方公式 逆向完全平方公式
I.(a+b)2=a2+2ab+b2 a2+2ab+b2=(a+b)2
II. (a-b)2 =[a+(-b)]2 a2-2ab+b2 =[a+(-b)]2
=a2-2ab+b2 = (a-b)2
例2 用完全平方式计算:
解:
计算下列各题,你能发现什么规律?
(1) (x+1)(x-1);
(2) (m+2)(m-2);
(3) (2x+1)(2x-1) ;
答案:
(x+1)(x-1)=_________;
(2) (m+2)(m-2)=__________;
(3) (2x+1)(2x-1)=________.
x2-1
m2-4
4x2-1
合作交流,探究新知
探究:
将长为(a+b),宽为(a-b)的长方形,剪下宽为b的长方形条(如图1),拼成有空缺的正方形(如图2),并请用等式表示你剪拼前后的图形的面积关系.?
(a+b)(a-b)=a2-b2.
图1
图2
活动探究
平方差公式:
(a+b)(a- b) =
a2- b2.
即两数和与这两数差的积等于这两个数的平方差.
(a+b)(a- b)=
a2- b2 .
a2- ab+ab- b2=
注:这里的两数可以是数字、字母、单项式也可以是两个多项式等.
例3 用平方差公式计算:
解:
运用平方差公式计算:
(1) (3x+2) (3x-2);
(2) (b+2a)(2a-b);
(3) (-x+2y) (-x-2y).
分析:在(1)中,可以把3x看成a,2看成b,即
(3x +2) ( 3x -2) = (3x)2 -22
(a + b) ( a - b) = a2 - b2
下列计算对不对?如果不对,怎样改正?
2)
错
1)
错
例4 计算:
解:
例5 计算:
解:
例6 计算:
解:
例7 计算:
解:
应用
1、直接应用
例1:利用完全平方公式计算.
(1) (2x+3)2 (2) (mn-a)2
2、灵活应用
例2:利用完全平方公式计算.
(-x+2y)2 (2)(-x-y)2
(3)(x+y-z)2 (4)(x+y)2-(x-y)2
3、简便算法
例3:计算.
(1) 1022 (2) 1972
活动与探究
1.已知x+y=8 xy=12 求x2+y2的值.
2.已知x2-2x+y2+6y+10=0 求x+y的值.
3.已知 a=2002x+2001 b=2002x+2002
c=2002x+2003
求a2+b2+c2-ab-bc-ac的值.
趣味题
一位老人非常喜欢孩子,每当有孩子到他家做客时,老人都拿出糖果招待他们,来一个孩子,老人就给这个孩子一块糖,来两个孩子,老人就给每个孩子两块糖……
1、第一天有a个男孩去了老人家,老人一共给了这些孩子多少块糖?
2、第二天有b个女孩去了老人家,老人一共给了这些孩子多少块糖?
3、第三天有(a+b)个孩子一块去看老人家,老人一共给了这些孩子多少块糖?
4、这些孩子第三天得到糖果数与前两天他们得到的糖果总数哪个多?多多少?为什么?
习题包
A:(3x-1)2=(3x)2-2(3x)( )+( )2
=9x2-6x+1.
B: (x+2)2=x2-kx+4 那么 k的值是( ).
A.-2 B.2 C.-4 D.4
C:不论x为何值(x+a)2=x2+x+a2则常数a等于( ).
A.2 B.-2 C.1/2 D.-1/2
D:若m2+km+36是一个完全平方式,则常数k=_________.
简便计算:
(1) 102×98;
(2) (y+2) (y-2) – (y-1) (y+5) .
解: (1)102×98
=(100+2)(100-2)
= 1002-22
=10000–4
= 9996.
(y+2)(y-2)-(y-1)(y+5)
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= -4y+1.
利用平方差公式计算:
(1)(a+3b)(a-3b);
(2)(3+2a)(-3+2a).
(3)51×49
(4)(x+y-1)(x+y+1)
快乐练习:
看谁做得最快最正确!
计算下列各题
轻松闯关:
1002×998 (转化思想)
(x+y)(x-y)(x2+y2) (灵活运用)
(3) (a+b)2-(a-b)2 (逆向思维训练)
运用完全平方公式计算:
解:
1.下面各式的计算错在哪里?应当怎样计算?
没有加乘积的2倍项,应改为:
没有减乘积的2倍项,平方项应该是加的,应改为:
2,计算下列各题:
平方差公式
这是两个特殊的多项式相乘.
两个数的和与这两个数差的积,等于它们的平方差.
3.运用乘法公式计算:
思维延伸
已知,两个正方形的周长之和等于32cm,它们的面积之差为48cm2,求这两个正方形的边长.
超越自我
谢谢聆听
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
