9.3 多项式乘多项式(第2课时)(共26张PPT)
文档属性
| 名称 | 9.3 多项式乘多项式(第2课时)(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 21:31:45 | ||
图片预览







文档简介
9.3 多项式乘多项式
第9章 整式乘法与因式分解
第2课时
2020-2021学年度苏科版七年级下册
(a+b)X=
aX+bX
当X=m+n时, (a+b)X=?
(a+b)(m+n)
=?
?
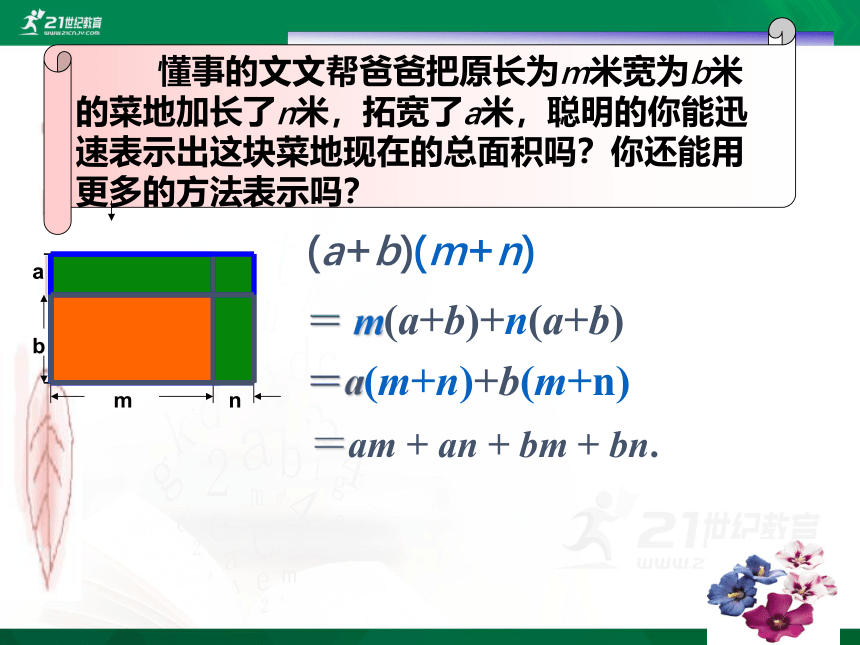
懂事的文文帮爸爸把原长为m米宽为b米的菜地加长了n米,拓宽了a米,聪明的你能迅速表示出这块菜地现在的总面积吗?你还能用更多的方法表示吗?
b
m
n
a
(1) (a+b)(m+n)
(2) m(a+b)+n(a+b)
(3) a(m+n)+b(m+n)
(4)am + an + bm + bn.
懂事的文文帮爸爸把原长为m米宽为b米的菜地加长了n米,拓宽了a米,聪明的你能迅速表示出这块菜地现在的总面积吗?你还能用更多的方法表示吗?
b
m
n
a
(a+b)(m+n)
= m(a+b)+n(a+b)
=a(m+n)+b(m+n)
=am + an + bm + bn.
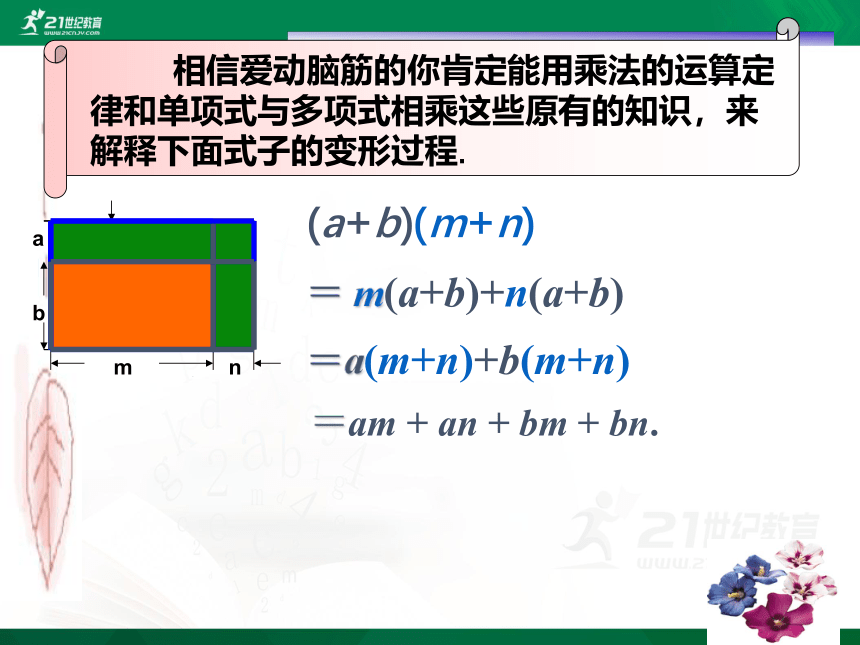
相信爱动脑筋的你肯定能用乘法的运算定律和单项式与多项式相乘这些原有的知识,来解释下面式子的变形过程.
b
m
n
a
(a+b)(m+n)
= m(a+b)+n(a+b)
=a(m+n)+b(m+n)
=am + an + bm + bn.
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
多项式的乘法法则:
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
(a+b)(m+n)=am+an+bm+bn
(a+b)X=
当X=m+n时, (a+b)X=?
(a+b)(m+n)
=?
试一试
计算:
(1)
(2)
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
直接利用:多项式乘以多项式的法则
参考解答:
例1 计算:
(1)(x+2)(x-3); (2)(3x-1)(x-2).
解:
例2 计算:
(1)(3m+n)(m-2n); (2)n(n+1)(n+2).
解:
计算:
学一学
?
(x+y)(2x-xy+3y)
辨一辨
?
判别下列解法是否正确,若错请说出理由.
解:原式
不正确
辨一辨
?
判别下列解法是否正确,若错请说出理由.
解:原式
延伸训练:
填空:
观察上面四个等式,你能发现什么规律?
你能根据这个规律解决下面的问题吗?
5 6
1 (-6)
(-1) (-6)
(-5) 6
口答:
计算:
1.(x+5)(x-7); 2.(x+5y)(x-7y);
3.(2m+3n)(2m-3n); 4.(2a+3b)2.
解:1.(x+5)(x-7)=x2-7x+5x-35
=x2-2x-35;
2.(x+5y)(x-7y)=x2-7xy+5xy-35y2
=x2-2xy-35y2;
4.(2a+3b)2=(2a+3b)(2a+3b)
3.(2m+3n)(2m-3n)=4m2-6mn+6mn-9n2
=4a2+12ab+9b2.
=4a2+6ab+6ab+9b2
=4m2-9n2;
1.计算:
2.一块长方形地砖的长、宽分别为acm、bcm(a>2,b>2).如果长、宽各裁去2cm,那么剩余部分的面积是多少?
1. 计算:
解:
1. 计算:
解:
1. 计算:
解:
课后思考
?
小东找来一张挂历画包数学课本,已知课本长a厘米,宽b厘米,厚c厘米,小东想将课本封面与封底的每一边都包进去m厘米.问小东应在挂历画上裁下一块多大面积的长方形?
谢谢聆听
第9章 整式乘法与因式分解
第2课时
2020-2021学年度苏科版七年级下册
(a+b)X=
aX+bX
当X=m+n时, (a+b)X=?
(a+b)(m+n)
=?
?
懂事的文文帮爸爸把原长为m米宽为b米的菜地加长了n米,拓宽了a米,聪明的你能迅速表示出这块菜地现在的总面积吗?你还能用更多的方法表示吗?
b
m
n
a
(1) (a+b)(m+n)
(2) m(a+b)+n(a+b)
(3) a(m+n)+b(m+n)
(4)am + an + bm + bn.
懂事的文文帮爸爸把原长为m米宽为b米的菜地加长了n米,拓宽了a米,聪明的你能迅速表示出这块菜地现在的总面积吗?你还能用更多的方法表示吗?
b
m
n
a
(a+b)(m+n)
= m(a+b)+n(a+b)
=a(m+n)+b(m+n)
=am + an + bm + bn.
相信爱动脑筋的你肯定能用乘法的运算定律和单项式与多项式相乘这些原有的知识,来解释下面式子的变形过程.
b
m
n
a
(a+b)(m+n)
= m(a+b)+n(a+b)
=a(m+n)+b(m+n)
=am + an + bm + bn.
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
多项式的乘法法则:
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
(a+b)(m+n)=am+an+bm+bn
(a+b)X=
当X=m+n时, (a+b)X=?
(a+b)(m+n)
=?
试一试
计算:
(1)
(2)
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
直接利用:多项式乘以多项式的法则
参考解答:
例1 计算:
(1)(x+2)(x-3); (2)(3x-1)(x-2).
解:
例2 计算:
(1)(3m+n)(m-2n); (2)n(n+1)(n+2).
解:
计算:
学一学
?
(x+y)(2x-xy+3y)
辨一辨
?
判别下列解法是否正确,若错请说出理由.
解:原式
不正确
辨一辨
?
判别下列解法是否正确,若错请说出理由.
解:原式
延伸训练:
填空:
观察上面四个等式,你能发现什么规律?
你能根据这个规律解决下面的问题吗?
5 6
1 (-6)
(-1) (-6)
(-5) 6
口答:
计算:
1.(x+5)(x-7); 2.(x+5y)(x-7y);
3.(2m+3n)(2m-3n); 4.(2a+3b)2.
解:1.(x+5)(x-7)=x2-7x+5x-35
=x2-2x-35;
2.(x+5y)(x-7y)=x2-7xy+5xy-35y2
=x2-2xy-35y2;
4.(2a+3b)2=(2a+3b)(2a+3b)
3.(2m+3n)(2m-3n)=4m2-6mn+6mn-9n2
=4a2+12ab+9b2.
=4a2+6ab+6ab+9b2
=4m2-9n2;
1.计算:
2.一块长方形地砖的长、宽分别为acm、bcm(a>2,b>2).如果长、宽各裁去2cm,那么剩余部分的面积是多少?
1. 计算:
解:
1. 计算:
解:
1. 计算:
解:
课后思考
?
小东找来一张挂历画包数学课本,已知课本长a厘米,宽b厘米,厚c厘米,小东想将课本封面与封底的每一边都包进去m厘米.问小东应在挂历画上裁下一块多大面积的长方形?
谢谢聆听
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
