9.4 乘法公式(第2课时)(共41张PPT)
文档属性
| 名称 | 9.4 乘法公式(第2课时)(共41张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 21:34:55 | ||
图片预览









文档简介
第2课时
9.4 乘法公式
第9章 整式乘法与因式分解
2020-2021学年度苏科版七年级下册
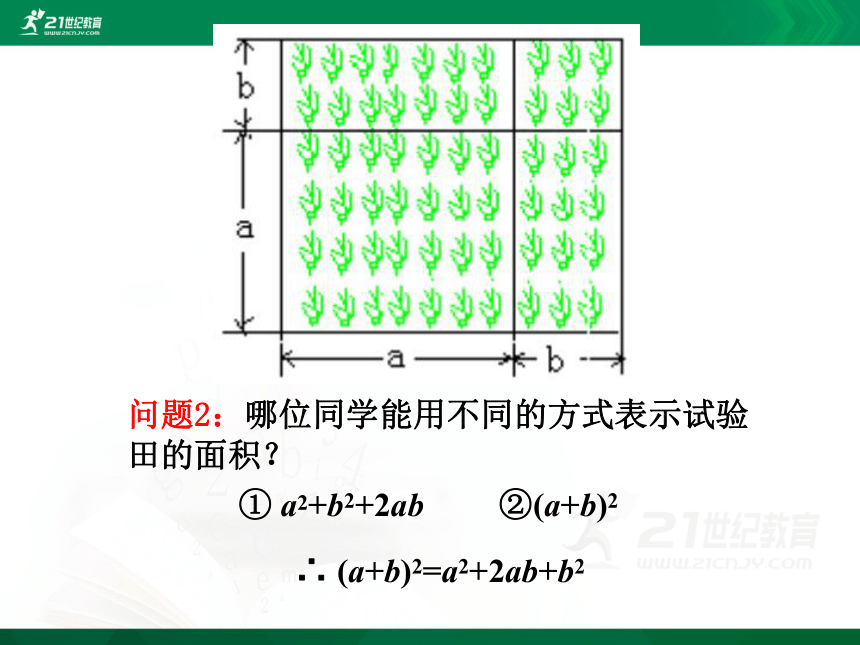
去年,一位农民在一次“科技下乡”活动中得到启示,将一块边长为a米的正方形农田改成试验田,种上了优质的杂交水稻,一年来,收益很大,今年,又一次“科技下乡”活动,使老农铁了心,要走科技兴农的路子,于是他想把原来的试验田,边长增加b米,形成四块试验田,种植不同的新品种.
问题1:同学们,谁来帮老爷爷实现这个愿望呢?
问题2:哪位同学能用不同的方式表示试验田的面积?
① a2+b2+2ab ②(a+b)2
∴ (a+b)2=a2+2ab+b2
完全平方公式的数学表达式:
完全平方公式的文字叙述:
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
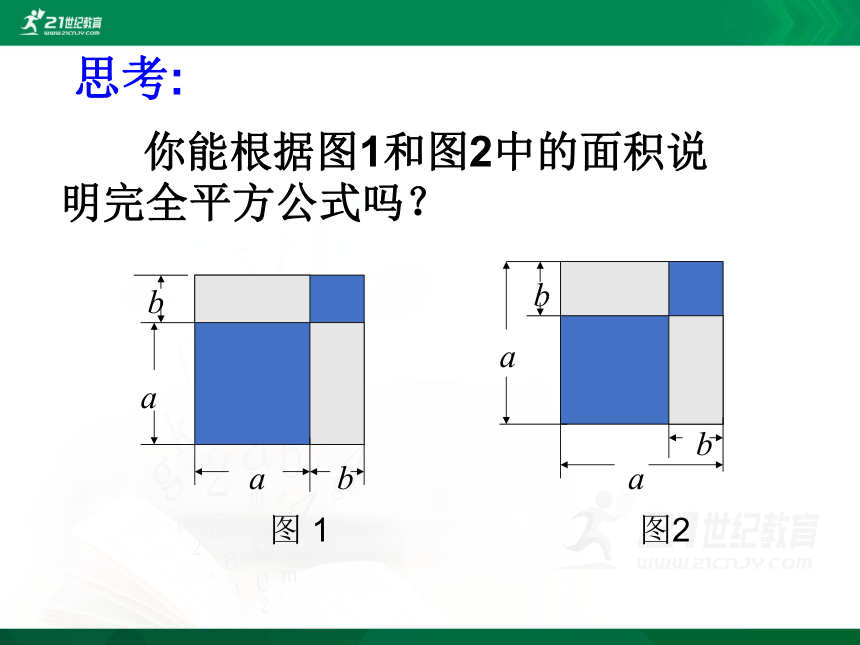
你能根据图1和图2中的面积说明完全平方公式吗?
b
a
a
b
b
a
b
a
图 1
图2
思考:
b
b
a
a
(a+b)?
a?
b?
ab
ab
+
+
和的完全平方公式:
完全平方公式 的几何意义
a
a
b
b
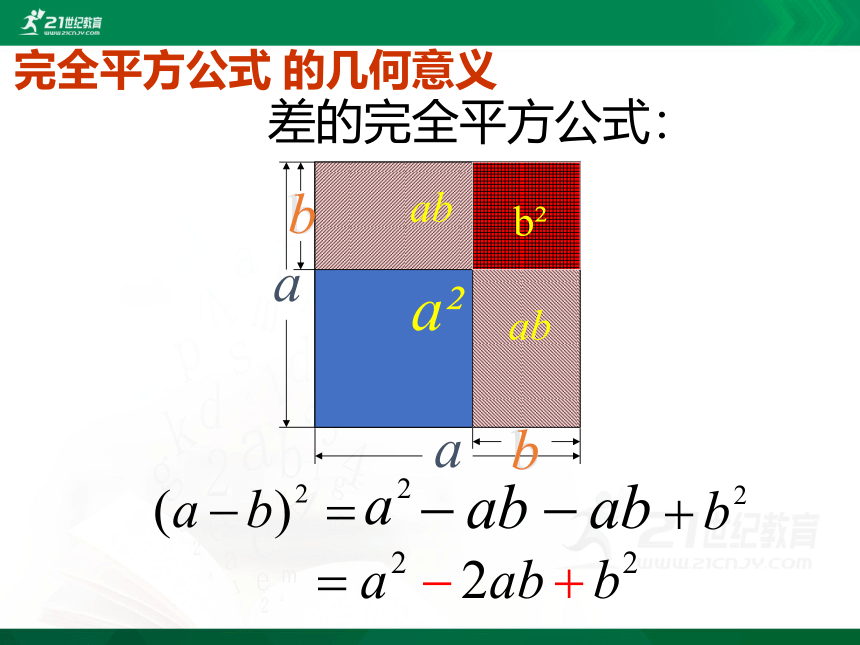
(a-b)?
a?
ab
ab
b?
b
b
差的完全平方公式:
完全平方公式 的几何意义
公式特征:
4、公式中的字母a,b可以表示数、单项 式和多项式.
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、积为二次三项式;
2、积中两项为两数的平方和;
3、另一项是两数积的2倍,且与乘式中
间的符号相同.
首平方,尾平方,积的2倍放中央 .
下面各式的计算是否正确?如果不正确,应当怎样改正?
(x+y)2=x2 +y2
(2)(x-y)2 =x2 -y2
(3) (-x+y)2 =x2+2xy+y2
(4) (2x+y)2 =4x2 +2xy +y2
错
错
错
错
(x+y)2 =x2+2xy+y2
(x-y)2 =x2 -2xy+y2
(-x+y)2 =x2-2xy+y2
(2x+y)2 =4x2+4xy +y2
想一想:
例1 计算:(a-b)2
解:
思考
(a+b)2与(-a-b)2相等吗?
(a-b)2与(b-a)2相等吗?
(a-b)2与a2-b2相等吗?
为什么?
例2 用完全平方式计算:
解:
1、运用完全平方公式计算:
解: (4m+n)2=
=16m2
(1)(4m+n)2
(a +b)2= a2 + 2 a b + b2
(4m)2
+2·(4m)·n
+n2
+8mn
+n2
解: (x-2y)2=
=x2
(2)(x-2y)2
(a -b)2= a2 - 2 ab + b2
x2
-2·x·2y
+(2y)2
-4xy
+4y2
(1) 1022
解: 1022
= (100+2)2
=10000+400+4
=10404.
(2) 992
解: 992
= (100 –1)2
=10000 -200+1
=9801.
2、运用完全平方公式计算:
观察等式
比较等号两边的式子,等号的左边有什么特征?等号的右边有什么特征?
大胆猜想
两数和
两数差
两数平方差
两数和与这两数差的积等于这两数的平方差.
平方差公式
概括总结
(2)等号右边是这两个数(字母)的平方差.
平方差公式的特征:
(1)等号左边是两个数(字母)的和乘以这两个数(字母)的差.
注:必须符合平方差
公式特征的代数式才能
用平方差公式.
公式中的字母的意义很广泛,可以代表常数,单项式或多项式 .
平方差公式:
下图是一个边长为 a 的大正方形,割去一个边长为b 的小正方形.小明将绿色和黄色两部分拼成一个长方形.
问:小明能拼成功吗?
做一做
b
a
a
b
例3 用平方差公式计算:
解:
原图实际面积为:________________
长方形的面积为:_________________
b
a
a
b
a-b
b
b
a
b
解决问题
练一练
阅读算式,按要求填写下面的表格
2m
3n
(-2m+3n)(2m+3n)
3x
2
(2-3x)(2+3x)
5
x
(x+5)(x-5)
写成“a2-b2”的形式
与平方差公式中b对应的项
与平方差公式中a对应的项
算式
(3n)?-(2m)?
拓展练习:
1. =____;
2.若 是一个完全平方公式,
则 _______;
3.若 是一个完全平方公式,
则 _______;
1
运用平方差公式计算:
(2)
练一练
能力提高
1.由多项式乘法计算:
2.你能设计一个图形来说明上面的公式吗?
a2-b2
(a+b)(a-b)
b
b
a
a
a
b
a﹣b
∴ (a+b)(a-b) =a2-b2.
1.计算:
2.计算:
1.用完全平方公式计算:
2.下面的计算是否正确?如有错误,请改正.
不对
改正
不对
改正
3.填空:
(1)(a+____)2=a2+4ab+4b2;
(2)(2a+____)2=4a2+4ab+b2;
(3)(3x-____)2=9x2-12xy+______;
(4)(-x-____)2=x2+_____+1.
2b
2y
4y2
b
1
2x
4.一个正方形的边长为acm(a>6).若边长减少6cm,则这个正方形的面积减少了多少?
解:面积减少:a2-(a-6)2
=a2-(a2-12a+36)=12a-36.
1.用平方差公式计算:
2.下面的计算是否正确?如有错误,请改正.
不对
改正
不对
改正
3.填空:
(1)(x+___)(x-___)=x2-36;
(2)(m+___)(m-___)=m2-25n2;
(3)(a+b)(_____)=b2-a2;
(4) (_____)(1-x)=x4-1.
6
6
5n
5n
-1-x2
b-a
谢谢聆听
9.4 乘法公式
第9章 整式乘法与因式分解
2020-2021学年度苏科版七年级下册
去年,一位农民在一次“科技下乡”活动中得到启示,将一块边长为a米的正方形农田改成试验田,种上了优质的杂交水稻,一年来,收益很大,今年,又一次“科技下乡”活动,使老农铁了心,要走科技兴农的路子,于是他想把原来的试验田,边长增加b米,形成四块试验田,种植不同的新品种.
问题1:同学们,谁来帮老爷爷实现这个愿望呢?
问题2:哪位同学能用不同的方式表示试验田的面积?
① a2+b2+2ab ②(a+b)2
∴ (a+b)2=a2+2ab+b2
完全平方公式的数学表达式:
完全平方公式的文字叙述:
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
你能根据图1和图2中的面积说明完全平方公式吗?
b
a
a
b
b
a
b
a
图 1
图2
思考:
b
b
a
a
(a+b)?
a?
b?
ab
ab
+
+
和的完全平方公式:
完全平方公式 的几何意义
a
a
b
b
(a-b)?
a?
ab
ab
b?
b
b
差的完全平方公式:
完全平方公式 的几何意义
公式特征:
4、公式中的字母a,b可以表示数、单项 式和多项式.
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、积为二次三项式;
2、积中两项为两数的平方和;
3、另一项是两数积的2倍,且与乘式中
间的符号相同.
首平方,尾平方,积的2倍放中央 .
下面各式的计算是否正确?如果不正确,应当怎样改正?
(x+y)2=x2 +y2
(2)(x-y)2 =x2 -y2
(3) (-x+y)2 =x2+2xy+y2
(4) (2x+y)2 =4x2 +2xy +y2
错
错
错
错
(x+y)2 =x2+2xy+y2
(x-y)2 =x2 -2xy+y2
(-x+y)2 =x2-2xy+y2
(2x+y)2 =4x2+4xy +y2
想一想:
例1 计算:(a-b)2
解:
思考
(a+b)2与(-a-b)2相等吗?
(a-b)2与(b-a)2相等吗?
(a-b)2与a2-b2相等吗?
为什么?
例2 用完全平方式计算:
解:
1、运用完全平方公式计算:
解: (4m+n)2=
=16m2
(1)(4m+n)2
(a +b)2= a2 + 2 a b + b2
(4m)2
+2·(4m)·n
+n2
+8mn
+n2
解: (x-2y)2=
=x2
(2)(x-2y)2
(a -b)2= a2 - 2 ab + b2
x2
-2·x·2y
+(2y)2
-4xy
+4y2
(1) 1022
解: 1022
= (100+2)2
=10000+400+4
=10404.
(2) 992
解: 992
= (100 –1)2
=10000 -200+1
=9801.
2、运用完全平方公式计算:
观察等式
比较等号两边的式子,等号的左边有什么特征?等号的右边有什么特征?
大胆猜想
两数和
两数差
两数平方差
两数和与这两数差的积等于这两数的平方差.
平方差公式
概括总结
(2)等号右边是这两个数(字母)的平方差.
平方差公式的特征:
(1)等号左边是两个数(字母)的和乘以这两个数(字母)的差.
注:必须符合平方差
公式特征的代数式才能
用平方差公式.
公式中的字母的意义很广泛,可以代表常数,单项式或多项式 .
平方差公式:
下图是一个边长为 a 的大正方形,割去一个边长为b 的小正方形.小明将绿色和黄色两部分拼成一个长方形.
问:小明能拼成功吗?
做一做
b
a
a
b
例3 用平方差公式计算:
解:
原图实际面积为:________________
长方形的面积为:_________________
b
a
a
b
a-b
b
b
a
b
解决问题
练一练
阅读算式,按要求填写下面的表格
2m
3n
(-2m+3n)(2m+3n)
3x
2
(2-3x)(2+3x)
5
x
(x+5)(x-5)
写成“a2-b2”的形式
与平方差公式中b对应的项
与平方差公式中a对应的项
算式
(3n)?-(2m)?
拓展练习:
1. =____;
2.若 是一个完全平方公式,
则 _______;
3.若 是一个完全平方公式,
则 _______;
1
运用平方差公式计算:
(2)
练一练
能力提高
1.由多项式乘法计算:
2.你能设计一个图形来说明上面的公式吗?
a2-b2
(a+b)(a-b)
b
b
a
a
a
b
a﹣b
∴ (a+b)(a-b) =a2-b2.
1.计算:
2.计算:
1.用完全平方公式计算:
2.下面的计算是否正确?如有错误,请改正.
不对
改正
不对
改正
3.填空:
(1)(a+____)2=a2+4ab+4b2;
(2)(2a+____)2=4a2+4ab+b2;
(3)(3x-____)2=9x2-12xy+______;
(4)(-x-____)2=x2+_____+1.
2b
2y
4y2
b
1
2x
4.一个正方形的边长为acm(a>6).若边长减少6cm,则这个正方形的面积减少了多少?
解:面积减少:a2-(a-6)2
=a2-(a2-12a+36)=12a-36.
1.用平方差公式计算:
2.下面的计算是否正确?如有错误,请改正.
不对
改正
不对
改正
3.填空:
(1)(x+___)(x-___)=x2-36;
(2)(m+___)(m-___)=m2-25n2;
(3)(a+b)(_____)=b2-a2;
(4) (_____)(1-x)=x4-1.
6
6
5n
5n
-1-x2
b-a
谢谢聆听
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
