9.2 单项式乘多项式(第1课时)(共25张PPT)
文档属性
| 名称 | 9.2 单项式乘多项式(第1课时)(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 00:00:00 | ||
图片预览








文档简介
9.2 单项式乘多项式
第1课时
第9章 整式乘法与因式分解
2020-2021学年度苏科版七年级下册
如何进行单项式乘单项式的运算?
单项式的系数?
相同字母的幂?
只在一个单项式里含有的字母?
单项式与单项式相乘:
单×单=(系数×系数)(同底数幂×同底数幂)(单独的幂)
知识 & 回顾
?
?
( 2a2b3c) (-3ab)
= -6a3b4c
口答计算结果:
m
a
b
c
ma
mb
mc
某街道为美化环境,对街道进行了大整治.其中一项就是把一块矩形的空地补上了彩色地砖(如下图),成为市民休闲健身的场所.
你能够表示出这块矩形空地的面积吗?
=
情景 & 导入
?
?
=
你能用所学的知识解释这个等式吗 ?
m(a+b+c)=
ma
mb
mc
+
+
2a2(3a2-5b)=
2a2.3a2
2a2.(-5b)
+
=6a4-10a2b
(-2a2)(3ab2-5b)=
(-2a2).3ab2
(-2a2).(-5b)
+
=-6a3b2+10a2b
类似的:
乘法分配律
单项式与多项式相乘,只要将单项式分别乘以多项式的各项,再将所得的积相加.
单项式与多项式相乘的法则:
例1 计算:
解:
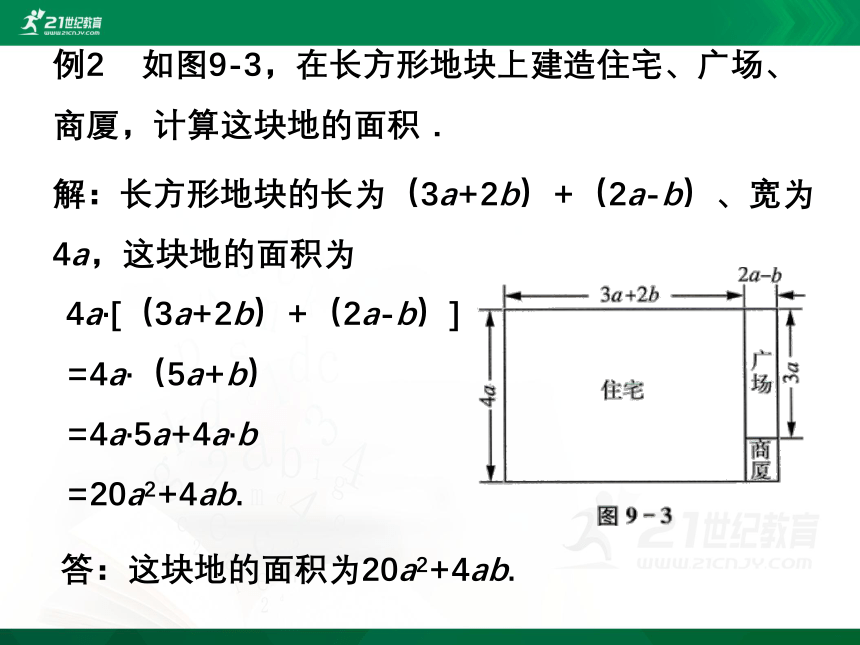
例2 如图9-3,在长方形地块上建造住宅、广场、商厦,计算这块地的面积.
解:长方形地块的长为(3a+2b)+(2a-b)、宽为4a,这块地的面积为
4a·[(3a+2b)+(2a-b)]
=4a·(5a+b)
=4a·5a+4a·b
=20a2+4ab.
答:这块地的面积为20a2+4ab.
感受新知----算一算
①
②
③
下列各题的解法是否正确,如果错了,指出错在什么地方,并改正过来.
×
×
×
辩一辩
7x-(x-3)x-3x(2-x)=(2x+1)x+6
解:去括号,得
7x-x2+3x-6x+3x2=2x2+x+6
移项,得7x-x2+3x-6x+3x2-2x2-x=6
合并同类项,得 3x = 6
系数化为1,得 x = 2.
深入探索----解一解
解不等式:
深入探索----解一解
解:去括号得:
>
移项合并得:
2x>-5
解得:x>
单项式与多项式相乘的法则:
单项式与多项式相乘,只要将单项式分别乘以多项式的各项,再将所得的积相加.
=
回顾 & 思考
?
?
② 再把所得的积相加.
① 用单项式分别去乘多项式的每一项;
运算时要注意哪些问题?
① 不能漏乘:
即单项式要乘遍多项式的每一项.
② 去括号时注意符号的确定.
2.(3x2y-xy2)·(-3xy)
1.计算
1.(-2ab)3(5a2b–2b3)
3.-2a2·(ab+b2)-5a(a2b-ab2)
yn(yn +9y-12)-3(3yn+1-4yn),
其中y=-3,n=2.
解: yn(yn + 9y-12)-3(3yn+1-4yn)
=y2n+9yn+1-12yn-9yn+1+12yn
=y2n.
当y=-3,n=2时,
原式=(-3)2×2=(-3)4=81.
2、先化简,再求值:
3、计算:2a2·(3a2-5b)
解:
=2a2·3a2-2a2·5b
2a2·(3a2-5b)
=6a4-10a2b.
计算3xy[2xy-x(y-2)+x].
=3xy·2xy-3xy·x(y-2)+3xy·x
=6x2y2-3xy·(xy-2x)+3x2y
=6x2y2-3x2y2+6x2y+3x2y
=3x2y2+9x2y.
解:3xy[2xy-x(y-2)+x]
(乘法分配律)
(单项式与单项式相乘)
(1)3x2y·(2xy2-3xy);
(2)2x·(3x2-xy+y2).
解:(1)3x2y·(2xy2-3xy)
=3x2y·2xy2-3x2y·3xy
=6x3y3-9x3y2;
1.计算:
(2)2x·(3x2-xy+y2).
=2x·3x2-2x·xy+2x·y2
=6x3-2x2y+2xy2.
=x3-x+2x3+2x-6x2+15x
解:x(x2-1)+2x2(x+1)-3x(2x-5)
2.化简:x(x2-1)+2x2(x+1)-3x(2x-5).
=3x3-6x2+16x.
1.计算:
2.化简:
3.某长方体的长为a+1,宽为a,高为3,问这个长方形的体积是多少?
谢谢聆听
第1课时
第9章 整式乘法与因式分解
2020-2021学年度苏科版七年级下册
如何进行单项式乘单项式的运算?
单项式的系数?
相同字母的幂?
只在一个单项式里含有的字母?
单项式与单项式相乘:
单×单=(系数×系数)(同底数幂×同底数幂)(单独的幂)
知识 & 回顾
?
?
( 2a2b3c) (-3ab)
= -6a3b4c
口答计算结果:
m
a
b
c
ma
mb
mc
某街道为美化环境,对街道进行了大整治.其中一项就是把一块矩形的空地补上了彩色地砖(如下图),成为市民休闲健身的场所.
你能够表示出这块矩形空地的面积吗?
=
情景 & 导入
?
?
=
你能用所学的知识解释这个等式吗 ?
m(a+b+c)=
ma
mb
mc
+
+
2a2(3a2-5b)=
2a2.3a2
2a2.(-5b)
+
=6a4-10a2b
(-2a2)(3ab2-5b)=
(-2a2).3ab2
(-2a2).(-5b)
+
=-6a3b2+10a2b
类似的:
乘法分配律
单项式与多项式相乘,只要将单项式分别乘以多项式的各项,再将所得的积相加.
单项式与多项式相乘的法则:
例1 计算:
解:
例2 如图9-3,在长方形地块上建造住宅、广场、商厦,计算这块地的面积.
解:长方形地块的长为(3a+2b)+(2a-b)、宽为4a,这块地的面积为
4a·[(3a+2b)+(2a-b)]
=4a·(5a+b)
=4a·5a+4a·b
=20a2+4ab.
答:这块地的面积为20a2+4ab.
感受新知----算一算
①
②
③
下列各题的解法是否正确,如果错了,指出错在什么地方,并改正过来.
×
×
×
辩一辩
7x-(x-3)x-3x(2-x)=(2x+1)x+6
解:去括号,得
7x-x2+3x-6x+3x2=2x2+x+6
移项,得7x-x2+3x-6x+3x2-2x2-x=6
合并同类项,得 3x = 6
系数化为1,得 x = 2.
深入探索----解一解
解不等式:
深入探索----解一解
解:去括号得:
>
移项合并得:
2x>-5
解得:x>
单项式与多项式相乘的法则:
单项式与多项式相乘,只要将单项式分别乘以多项式的各项,再将所得的积相加.
=
回顾 & 思考
?
?
② 再把所得的积相加.
① 用单项式分别去乘多项式的每一项;
运算时要注意哪些问题?
① 不能漏乘:
即单项式要乘遍多项式的每一项.
② 去括号时注意符号的确定.
2.(3x2y-xy2)·(-3xy)
1.计算
1.(-2ab)3(5a2b–2b3)
3.-2a2·(ab+b2)-5a(a2b-ab2)
yn(yn +9y-12)-3(3yn+1-4yn),
其中y=-3,n=2.
解: yn(yn + 9y-12)-3(3yn+1-4yn)
=y2n+9yn+1-12yn-9yn+1+12yn
=y2n.
当y=-3,n=2时,
原式=(-3)2×2=(-3)4=81.
2、先化简,再求值:
3、计算:2a2·(3a2-5b)
解:
=2a2·3a2-2a2·5b
2a2·(3a2-5b)
=6a4-10a2b.
计算3xy[2xy-x(y-2)+x].
=3xy·2xy-3xy·x(y-2)+3xy·x
=6x2y2-3xy·(xy-2x)+3x2y
=6x2y2-3x2y2+6x2y+3x2y
=3x2y2+9x2y.
解:3xy[2xy-x(y-2)+x]
(乘法分配律)
(单项式与单项式相乘)
(1)3x2y·(2xy2-3xy);
(2)2x·(3x2-xy+y2).
解:(1)3x2y·(2xy2-3xy)
=3x2y·2xy2-3x2y·3xy
=6x3y3-9x3y2;
1.计算:
(2)2x·(3x2-xy+y2).
=2x·3x2-2x·xy+2x·y2
=6x3-2x2y+2xy2.
=x3-x+2x3+2x-6x2+15x
解:x(x2-1)+2x2(x+1)-3x(2x-5)
2.化简:x(x2-1)+2x2(x+1)-3x(2x-5).
=3x3-6x2+16x.
1.计算:
2.化简:
3.某长方体的长为a+1,宽为a,高为3,问这个长方形的体积是多少?
谢谢聆听
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
