2020——2021学年鲁教版(五四制)数学九年级下册 5.10 圆锥的侧面积 同步练习(word版含解析)
文档属性
| 名称 | 2020——2021学年鲁教版(五四制)数学九年级下册 5.10 圆锥的侧面积 同步练习(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 210.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 23:02:54 | ||
图片预览




文档简介
5.10 圆锥的侧面积
一.选择题
1.下列说法正确的是( )
A.圆有无数条对称轴,每一条直径都是它的一条对称轴
B.比的前项和后项同时乘或除以相同的数,比值不变
C.一种商品先提价,然后再降价,现在和原价一样
D.圆锥的底面半径扩大到原来的2倍,高不变,则它的体积扩大到原来的4倍
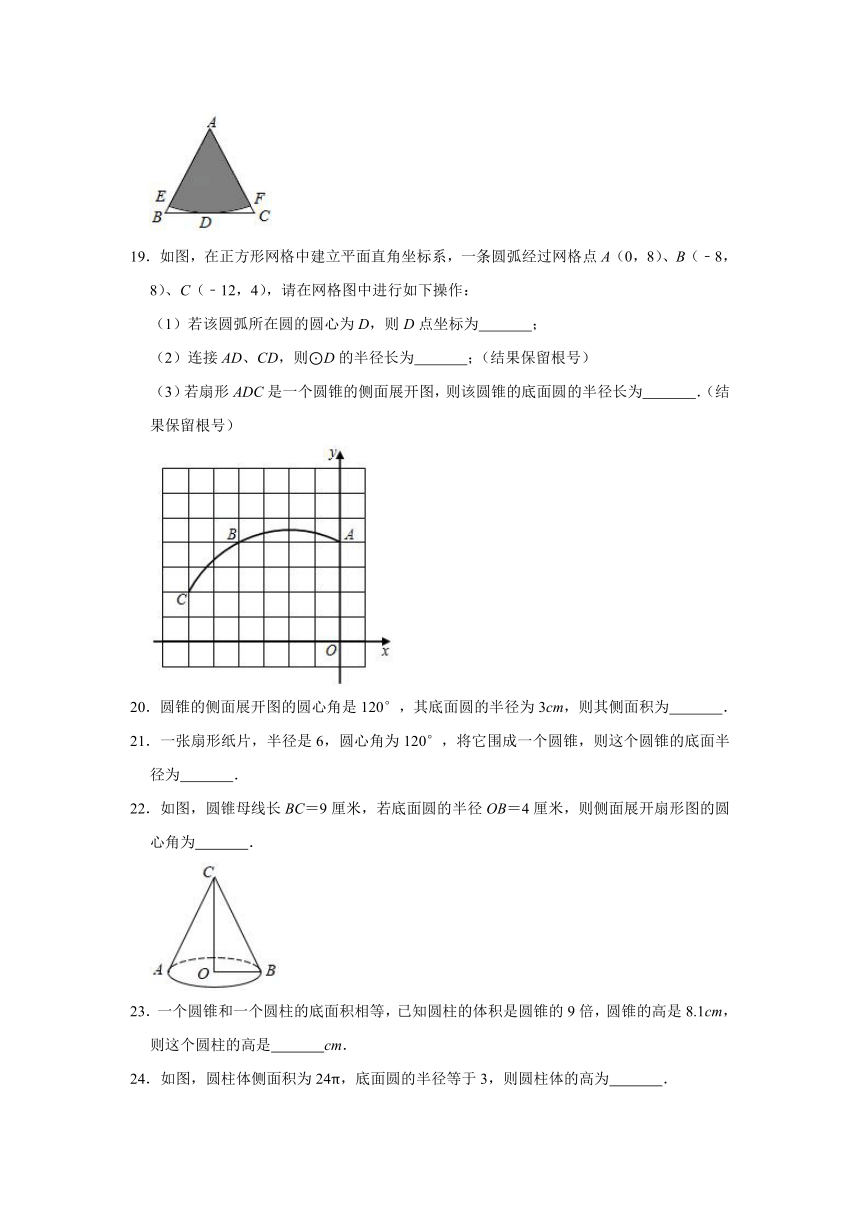
2.用一个圆心角为120°,半径为4的扇形,做一个圆锥的侧面,则这个圆锥的全面积(侧面与底面面积的和)为( )
A. B. C. D.
3.一个圆锥的母线长为4cm,底面圆的半径为3cm,则这个圆锥的侧面积为( )
A.12πcm2 B.15πcm2 C.20πcm2 D.30πcm2
4.如图,从一圆形纸片上剪出一个半径为R,圆心角为90°的扇形和一半径为r的圆,使之恰好围成如图所示的圆锥,则R与r的关系为( )
A.R=2r B.R=4r C.R=2r D.R=6r
5.已知圆锥的底面半径是4,母线长是5,则圆锥的侧面积是( )
A.10π B.15π C.20π D.25π
6.已知圆锥的母线长是4cm,侧面积是12πcm2,则这个圆锥底面圆的半径是( )
A.3cm B.4cm C.5cm D.6cm
7.在△ABC中,∠C=90°,AC=12,BC=5,现以AC为轴旋转一周得到一个圆锥.则该圆锥的侧面积为( )
A.130π B.90π C.25π D.65π
8.已知圆锥的底面半径为2cm,母线长为3cm,则它的侧面展开图的面积为( )
A.18πcm2 B.12πcm2 C.6πcm2 D.3πcm2
9.如图,已知圆锥的母线长为6,圆锥的高与母线所夹的角为θ,且sinθ=,则该圆锥的侧面积是( )
A.24 B.24π C.16π D.12π
10.如果圆锥的母线长为5cm,底面半径为3cm,那么这个圆锥的全面积是( )
A.12π B.15π C.20π D.24π
11.已知圆锥的底面半径为6cm,母线长为10cm,则这个圆锥的全面积是( )
A.60πcm2 B.96πcm2 C.132πcm2 D.168πcm2
12.如图,从一块半径为20cm的圆形铁皮上剪出一个圆心角是60°的扇形ABC,则此扇形围成的圆锥的侧面积为( )
A.200πcm2 B.100πcm2 C.100πcm2 D.50πcm2
13.如图,粮仓的顶部是圆锥形状,这个圆锥底面的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元钱,那么购买油毡所需要的费用是( )
A.540π元 B.360π元 C.180π元 D.90π元
14.如图,一只蚂蚁要从圆柱体下底面的A点,沿圆柱表面爬到与A相对的上底面的B点,圆柱底面直径为4,母线为6,则蚂蚁爬行的最短路线长为( )
A. B. C.4π D.6π
15.如图,把一个棱长是40厘米的正方体削成一个最大的圆柱体,圆柱的侧面积是多少平方厘米?正确的列式是( )
A.40×40×6
B.()2×3.14×40
C.40×3.14×40
D.40×3.14×40+()2×3.14×2
二.填空题
16.如图,粮仓的顶部是圆锥形状,这个圆锥的底面圆的半径为3米,母线长为6米,为防雨水,需要在粮仓顶部铺上油毡,如果油毡的市场价为10元/米2,那么购买油毡所需要的费用是 元(结果保留π).
17.用一个圆心角为180°,半径为6的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径是 .
18.如图,从一块边长为2的等边三角形卡纸上剪下一个面积最大的扇形,并将其围成一个圆锥,则圆锥的底面圆的半径是 .
19.如图,在正方形网格中建立平面直角坐标系,一条圆弧经过网格点A(0,8)、B(﹣8,8)、C(﹣12,4),请在网格图中进行如下操作:
(1)若该圆弧所在圆的圆心为D,则D点坐标为 ;
(2)连接AD、CD,则⊙D的半径长为 ;(结果保留根号)
(3)若扇形ADC是一个圆锥的侧面展开图,则该圆锥的底面圆的半径长为 .(结果保留根号)
20.圆锥的侧面展开图的圆心角是120°,其底面圆的半径为3cm,则其侧面积为 .
21.一张扇形纸片,半径是6,圆心角为120°,将它围成一个圆锥,则这个圆锥的底面半径为 .
22.如图,圆锥母线长BC=9厘米,若底面圆的半径OB=4厘米,则侧面展开扇形图的圆心角为 .
23.一个圆锥和一个圆柱的底面积相等,已知圆柱的体积是圆锥的9倍,圆锥的高是8.1cm,则这个圆柱的高是 cm.
24.如图,圆柱体侧面积为24π,底面圆的半径等于3,则圆柱体的高为 .
25.一个圆柱的底面半径是3.2dm,高5dm,则这个圆柱的侧面积为 dm2.(π取3.14)
三.解答题
26.一个圆锥形沙堆,底面半径是5米,高是2.5米.(π取3)
(1)求这堆沙子有多少立方米?
(2)用这堆沙子在10m宽的公路上铺2cm厚的路面,能铺多少米?
(3)在(2)的条件下,一台压路机的前轮直径是1m,前轮宽度是2m.如果前轮每分钟转动6周,这台压路机压一遍这段路面大约需要多少分钟?(得数保留整数.)
27.如图1,圆锥底面圆半径为1,母线长为4,图2为其侧面展开图.
(1)求阴影部分面积;
(2)母线SC是一条蜜糖线,一只蚂蚁从A沿着圆锥侧面最少需要爬多远才能吃到蜜糖?
28.如图,已知矩形ABCD的周长为36cm,矩形绕它的一条边CD旋转形成一个圆柱.设矩形的一边AB的长为xcm(x>0),旋转形成的圆柱的侧面积为Scm2.
(1)用含x的式子表示:
矩形的另一边BC的长为 cm,旋转形成的圆柱的底面圆的周长为 cm;
(2)求S关于x的函数解析式及自变量x的取值范围;
(3)求当x取何值时,矩形旋转形成的圆柱的侧面积最大;
(4)若矩形旋转形成的圆柱的侧面积等于18πcm2,则矩形的长是 cm,宽是 cm.
29.如图①,水平放置的空圆柱形容器内放着一个实心的铁“柱锥体”(由一个高为5cm的圆柱和一个同底面的高为3cm圆锥组成的铁几何体).向这个容器内匀速注水,水流速度为5cm3/s,注满为止.整个注水过程中,水面高度h(cm)与注水时间t(s)之间的函数关系如图②所示.
(1)圆柱形容器的高为 cm.
(2)求线段BC所对应的函数表达式.
(3)直接写出“柱锥体”顶端距离水面3.5cm时t的值.
30.如图①,已知圆锥的母线长l=16cm,若以顶点O为中心,将此圆锥按图②放置在平面上逆时针滚动3圈后所形成的扇形的圆心角θ=270°.
(1)求圆锥的底面半径;
(2)求圆锥的表面积.
参考答案
一.选择题
1.解:A、圆有无数条对称轴,每一条直径所在的直线都是它的一条对称轴,故原命题错误,不符合题意;
B、比的前项和后项同时乘或除以相同的数(不为零),比值不变,故原命题错误,不符合题意;
C、一种商品先提价,然后再降价,现在比原价低,故原命题错误,不符合题意;
D、圆锥的底面半径扩大到原来的2倍,高不变,则它的体积扩大到原来的4倍,正确,符合题意,
故选:D.
2.解:设圆锥的底面圆的半径为r,
根据题意得2πr=,解得r=,
所以这个圆锥的全面积=π×()2+=π.
故选:D.
3.解:底面圆半径为3cm,则底面周长=6π,圆锥的侧面积=×4π×3=12π(cm2).
故选:A.
4.解:∵恰好围成图2所示的一个圆锥模型,
∴圆锥的侧面展开扇形的弧长等于圆锥的底面周长,
∴=2πr,
解得:R=4r,
故选:B.
5.解:圆锥的侧面积=×2π×4×5=20π,
故选:C.
6.解:设圆锥的底面半径为rcm,
则×2πr×4=12π,
解得,r=3(cm),
故选:A.
7.解:∵∠C=90°,AC=12,BC=5,
∴AB==13,
∴该圆锥的侧面积=×2×π×5×13=65π,
故选:D.
8.解:它的侧面展开图的面积=?2π?2?3=6π(cm2).
故选:C.
9.解:∵sinθ=,母线长为6,
∴圆锥的底面半径=×6=2,
∴该圆锥的侧面积=×6×2π?2=12π.
故选:D.
10.解:∵圆锥的母线长为5cm,底面半径为3cm,
∴这个圆锥的全面积是:π×32+π×3×5=24π(cm2).
故选:D.
11.解:根据题意,这个圆锥的全面积=×2π×6×10+π×62=60π+36π=96π(cm2).
故选:B.
12.解:作OD⊥AB于D,如图,则AD=BD,
∵∠OAD=∠BAC=30°,
∴OD=OA=10,AD=OD=10,
∴AB=2AD=20,
∴扇形围成的圆锥的侧面积==200π(cm2).
故选:A.
13.解:底面半径为3m,则底面周长=6π,侧面面积=×6π×6=18π(m2).
所需要的费用=18π×10=180π(元),
故选:C.
14.解:把圆柱侧面展开,展开图如图所示,点A,B的最短距离为线段AB的长,
BC=6,AC为底面半圆弧长,AC=2π,
所以AB==.
故选:A.
15.解:∵把一个棱长是40厘米的正方体削成一个最大的圆柱体,
∴圆柱的高和底面的直径都等于正方形的棱长,
∴侧面积为πdh=40×3.14×40,
故选:C.
二.填空题
16.解:根据题意得:圆锥侧面积=π×3×6=18π(平方米),
则购买油毡所需要的费用=10×18π=180π(元).
故答案为:180π.
17.解:设圆锥的底面半径为r.
由题意,2πr=,
∴r=3,
故答案为:3.
18.解:连结AD,
∵△ABC是边长为2的等边三角形,
∴AD=2×=,
∴扇形的弧长为=π,
∴圆锥的底面圆的半径是π÷π÷2=.
故答案为:.
19.解:(1)如图,点D的坐标为(﹣4,0);
(2)在Rt△OAD中,AD==4,
即⊙D的半径长为4;
(3)设该圆锥的底面圆的半径长为r,
∵CD=AD=4,AC==4,
∴CD2+AD2=AC2,
∴△ACD为等腰直角三角形,∠ADC=90°,
根据题意得2πr=,解得r=,
即该圆锥的底面圆的半径长为.
故答案为(﹣4,0);4;.
20.解:∵底面圆的半径为3cm,
∴底面周长为6πcm,
∴侧面展开扇形的弧长为6πcm,
设扇形的半径为r,
∵圆锥的侧面展开图的圆心角是120°,
∴=6π,
解得:r=9,
∴侧面积为×6π×9=27π(cm2),
故答案为:27πcm2.
21.解:设圆锥的底面半径为r.
由题意,2π?r=,
∴r=2,
故答案为:2.
22.解:由题意知:弧长=圆锥底面周长=2×4π=8π(厘米),
设所求圆心角的度数为n°,
则=8π,解得n=160,
即侧面展开扇形图的圆心角为160°.
故答案为:160°.
23.解:设这个圆柱的高是xcm,圆锥和圆柱的底面积都为S,
根据题意得S?x=9××S×8.1,
解得x=24.3(cm),
即这个圆柱的高是24.3cm.
故答案为24.3.
24.解:设圆柱体的高为h,
∵圆柱体侧面积为24π,底面圆的半径等于3,
∴2π×3×h=24π,
解得:h=4,
故答案为:4.
25.解:侧面积=2×3.14×3.2×5=100.48(dm2).
故这个圆柱的侧面积为100.48dm2.
故答案为:100.48.
三.解答题
26.解:(1)圆锥的体积=×π×52×2.5=π≈60.25(立方米),
答:这堆沙子约有60.25立方米;
(2)用这堆沙子在10m宽的公路上铺2cm厚的路面,能铺的米数为:60.25÷(10×0.02)=301.25(米),
答:用这堆沙子在10m宽的公路上铺2cm厚的路面,能铺301.25米;
(3)压路机一分钟压的面积=π×1×2×6≈36(平方米),
则这台压路机压一遍这段路面大约需要的时间=301.25×10÷36≈84(分).
27.解:(1)如图2中,作SE⊥AF交弧AF于C.
设图2中的扇形的圆心角为n°,
根据题意得=2π?1,
∴n=90°,
∵SA=SF,
∴△SFA是等腰直角三角形,
∴AF=SF=4,SE=AF=2,
∴S阴=S扇形SAF﹣S△SAF=﹣××=4π﹣8;
(2)在图2中,∵SC是一条蜜糖线,AE⊥SC,AE=2,
∴一只蚂蚁从A沿着圆锥表面最少需要爬2个单位长度才能吃到蜜糖.
28.解:(1)BC=(36﹣2x)=(18﹣x)cm,
旋转形成的圆柱的底面圆的周长为2π(18﹣x)cm.
故答案为:(18﹣x),2π(18﹣x).
(2)S=2π(18﹣x)?x=﹣2πx2+36πx(0<x<18).
(3)∵S=﹣2πx2+36πx=﹣2π(x﹣9)2+162π,
又∵﹣2π<0,
∴x=9时,S有最大值.
(4)由题意:﹣2πx2+36πx=18π,
∴x2﹣18x+9=0,
解得x=9+6或9﹣6(舍弃),
∴矩形的长是(9+6)cm,宽是(9﹣6)cm.
故答案为:(9+6),(9﹣6).
29.解:(1)由题意和函数图象可得,
圆柱容器的高为12cm,
故答案为:12;
(2)BC过点(26,8),(42,12),
设线段BC所对应的函数表达式为h=kt+b,
将点(26,8),(42,12)代入,得
,
解得,
所以线段BC所对应的函数表达式为h=t+;
(3)以为“柱锥体”的高为:5+3=8(cm),
所以顶端距离水面3.5cm位置有2个,
①当h=8﹣3.5=4.5时,在OA上,
设OA解析式为h=kt,过点A(15,5),
所以15k=5,解得k=,
所以OA解析式为h=t,
当h=4.5时,t=13.5;
②当h=8+3.5=11.5时,在BC上,
将h=11.5代入h=t+,
解得t=40.
综上所述:“柱锥体”顶端距离水面3.5cm时t的值为13.5s或40s.
30.解:(1)由题意3×2πr=,
∴r=4.
(2)圆锥的表面积=π?42+?2π?4?16=80π.
一.选择题
1.下列说法正确的是( )
A.圆有无数条对称轴,每一条直径都是它的一条对称轴
B.比的前项和后项同时乘或除以相同的数,比值不变
C.一种商品先提价,然后再降价,现在和原价一样
D.圆锥的底面半径扩大到原来的2倍,高不变,则它的体积扩大到原来的4倍
2.用一个圆心角为120°,半径为4的扇形,做一个圆锥的侧面,则这个圆锥的全面积(侧面与底面面积的和)为( )
A. B. C. D.
3.一个圆锥的母线长为4cm,底面圆的半径为3cm,则这个圆锥的侧面积为( )
A.12πcm2 B.15πcm2 C.20πcm2 D.30πcm2
4.如图,从一圆形纸片上剪出一个半径为R,圆心角为90°的扇形和一半径为r的圆,使之恰好围成如图所示的圆锥,则R与r的关系为( )
A.R=2r B.R=4r C.R=2r D.R=6r
5.已知圆锥的底面半径是4,母线长是5,则圆锥的侧面积是( )
A.10π B.15π C.20π D.25π
6.已知圆锥的母线长是4cm,侧面积是12πcm2,则这个圆锥底面圆的半径是( )
A.3cm B.4cm C.5cm D.6cm
7.在△ABC中,∠C=90°,AC=12,BC=5,现以AC为轴旋转一周得到一个圆锥.则该圆锥的侧面积为( )
A.130π B.90π C.25π D.65π
8.已知圆锥的底面半径为2cm,母线长为3cm,则它的侧面展开图的面积为( )
A.18πcm2 B.12πcm2 C.6πcm2 D.3πcm2
9.如图,已知圆锥的母线长为6,圆锥的高与母线所夹的角为θ,且sinθ=,则该圆锥的侧面积是( )
A.24 B.24π C.16π D.12π
10.如果圆锥的母线长为5cm,底面半径为3cm,那么这个圆锥的全面积是( )
A.12π B.15π C.20π D.24π
11.已知圆锥的底面半径为6cm,母线长为10cm,则这个圆锥的全面积是( )
A.60πcm2 B.96πcm2 C.132πcm2 D.168πcm2
12.如图,从一块半径为20cm的圆形铁皮上剪出一个圆心角是60°的扇形ABC,则此扇形围成的圆锥的侧面积为( )
A.200πcm2 B.100πcm2 C.100πcm2 D.50πcm2
13.如图,粮仓的顶部是圆锥形状,这个圆锥底面的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元钱,那么购买油毡所需要的费用是( )
A.540π元 B.360π元 C.180π元 D.90π元
14.如图,一只蚂蚁要从圆柱体下底面的A点,沿圆柱表面爬到与A相对的上底面的B点,圆柱底面直径为4,母线为6,则蚂蚁爬行的最短路线长为( )
A. B. C.4π D.6π
15.如图,把一个棱长是40厘米的正方体削成一个最大的圆柱体,圆柱的侧面积是多少平方厘米?正确的列式是( )
A.40×40×6
B.()2×3.14×40
C.40×3.14×40
D.40×3.14×40+()2×3.14×2
二.填空题
16.如图,粮仓的顶部是圆锥形状,这个圆锥的底面圆的半径为3米,母线长为6米,为防雨水,需要在粮仓顶部铺上油毡,如果油毡的市场价为10元/米2,那么购买油毡所需要的费用是 元(结果保留π).
17.用一个圆心角为180°,半径为6的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径是 .
18.如图,从一块边长为2的等边三角形卡纸上剪下一个面积最大的扇形,并将其围成一个圆锥,则圆锥的底面圆的半径是 .
19.如图,在正方形网格中建立平面直角坐标系,一条圆弧经过网格点A(0,8)、B(﹣8,8)、C(﹣12,4),请在网格图中进行如下操作:
(1)若该圆弧所在圆的圆心为D,则D点坐标为 ;
(2)连接AD、CD,则⊙D的半径长为 ;(结果保留根号)
(3)若扇形ADC是一个圆锥的侧面展开图,则该圆锥的底面圆的半径长为 .(结果保留根号)
20.圆锥的侧面展开图的圆心角是120°,其底面圆的半径为3cm,则其侧面积为 .
21.一张扇形纸片,半径是6,圆心角为120°,将它围成一个圆锥,则这个圆锥的底面半径为 .
22.如图,圆锥母线长BC=9厘米,若底面圆的半径OB=4厘米,则侧面展开扇形图的圆心角为 .
23.一个圆锥和一个圆柱的底面积相等,已知圆柱的体积是圆锥的9倍,圆锥的高是8.1cm,则这个圆柱的高是 cm.
24.如图,圆柱体侧面积为24π,底面圆的半径等于3,则圆柱体的高为 .
25.一个圆柱的底面半径是3.2dm,高5dm,则这个圆柱的侧面积为 dm2.(π取3.14)
三.解答题
26.一个圆锥形沙堆,底面半径是5米,高是2.5米.(π取3)
(1)求这堆沙子有多少立方米?
(2)用这堆沙子在10m宽的公路上铺2cm厚的路面,能铺多少米?
(3)在(2)的条件下,一台压路机的前轮直径是1m,前轮宽度是2m.如果前轮每分钟转动6周,这台压路机压一遍这段路面大约需要多少分钟?(得数保留整数.)
27.如图1,圆锥底面圆半径为1,母线长为4,图2为其侧面展开图.
(1)求阴影部分面积;
(2)母线SC是一条蜜糖线,一只蚂蚁从A沿着圆锥侧面最少需要爬多远才能吃到蜜糖?
28.如图,已知矩形ABCD的周长为36cm,矩形绕它的一条边CD旋转形成一个圆柱.设矩形的一边AB的长为xcm(x>0),旋转形成的圆柱的侧面积为Scm2.
(1)用含x的式子表示:
矩形的另一边BC的长为 cm,旋转形成的圆柱的底面圆的周长为 cm;
(2)求S关于x的函数解析式及自变量x的取值范围;
(3)求当x取何值时,矩形旋转形成的圆柱的侧面积最大;
(4)若矩形旋转形成的圆柱的侧面积等于18πcm2,则矩形的长是 cm,宽是 cm.
29.如图①,水平放置的空圆柱形容器内放着一个实心的铁“柱锥体”(由一个高为5cm的圆柱和一个同底面的高为3cm圆锥组成的铁几何体).向这个容器内匀速注水,水流速度为5cm3/s,注满为止.整个注水过程中,水面高度h(cm)与注水时间t(s)之间的函数关系如图②所示.
(1)圆柱形容器的高为 cm.
(2)求线段BC所对应的函数表达式.
(3)直接写出“柱锥体”顶端距离水面3.5cm时t的值.
30.如图①,已知圆锥的母线长l=16cm,若以顶点O为中心,将此圆锥按图②放置在平面上逆时针滚动3圈后所形成的扇形的圆心角θ=270°.
(1)求圆锥的底面半径;
(2)求圆锥的表面积.
参考答案
一.选择题
1.解:A、圆有无数条对称轴,每一条直径所在的直线都是它的一条对称轴,故原命题错误,不符合题意;
B、比的前项和后项同时乘或除以相同的数(不为零),比值不变,故原命题错误,不符合题意;
C、一种商品先提价,然后再降价,现在比原价低,故原命题错误,不符合题意;
D、圆锥的底面半径扩大到原来的2倍,高不变,则它的体积扩大到原来的4倍,正确,符合题意,
故选:D.
2.解:设圆锥的底面圆的半径为r,
根据题意得2πr=,解得r=,
所以这个圆锥的全面积=π×()2+=π.
故选:D.
3.解:底面圆半径为3cm,则底面周长=6π,圆锥的侧面积=×4π×3=12π(cm2).
故选:A.
4.解:∵恰好围成图2所示的一个圆锥模型,
∴圆锥的侧面展开扇形的弧长等于圆锥的底面周长,
∴=2πr,
解得:R=4r,
故选:B.
5.解:圆锥的侧面积=×2π×4×5=20π,
故选:C.
6.解:设圆锥的底面半径为rcm,
则×2πr×4=12π,
解得,r=3(cm),
故选:A.
7.解:∵∠C=90°,AC=12,BC=5,
∴AB==13,
∴该圆锥的侧面积=×2×π×5×13=65π,
故选:D.
8.解:它的侧面展开图的面积=?2π?2?3=6π(cm2).
故选:C.
9.解:∵sinθ=,母线长为6,
∴圆锥的底面半径=×6=2,
∴该圆锥的侧面积=×6×2π?2=12π.
故选:D.
10.解:∵圆锥的母线长为5cm,底面半径为3cm,
∴这个圆锥的全面积是:π×32+π×3×5=24π(cm2).
故选:D.
11.解:根据题意,这个圆锥的全面积=×2π×6×10+π×62=60π+36π=96π(cm2).
故选:B.
12.解:作OD⊥AB于D,如图,则AD=BD,
∵∠OAD=∠BAC=30°,
∴OD=OA=10,AD=OD=10,
∴AB=2AD=20,
∴扇形围成的圆锥的侧面积==200π(cm2).
故选:A.
13.解:底面半径为3m,则底面周长=6π,侧面面积=×6π×6=18π(m2).
所需要的费用=18π×10=180π(元),
故选:C.
14.解:把圆柱侧面展开,展开图如图所示,点A,B的最短距离为线段AB的长,
BC=6,AC为底面半圆弧长,AC=2π,
所以AB==.
故选:A.
15.解:∵把一个棱长是40厘米的正方体削成一个最大的圆柱体,
∴圆柱的高和底面的直径都等于正方形的棱长,
∴侧面积为πdh=40×3.14×40,
故选:C.
二.填空题
16.解:根据题意得:圆锥侧面积=π×3×6=18π(平方米),
则购买油毡所需要的费用=10×18π=180π(元).
故答案为:180π.
17.解:设圆锥的底面半径为r.
由题意,2πr=,
∴r=3,
故答案为:3.
18.解:连结AD,
∵△ABC是边长为2的等边三角形,
∴AD=2×=,
∴扇形的弧长为=π,
∴圆锥的底面圆的半径是π÷π÷2=.
故答案为:.
19.解:(1)如图,点D的坐标为(﹣4,0);
(2)在Rt△OAD中,AD==4,
即⊙D的半径长为4;
(3)设该圆锥的底面圆的半径长为r,
∵CD=AD=4,AC==4,
∴CD2+AD2=AC2,
∴△ACD为等腰直角三角形,∠ADC=90°,
根据题意得2πr=,解得r=,
即该圆锥的底面圆的半径长为.
故答案为(﹣4,0);4;.
20.解:∵底面圆的半径为3cm,
∴底面周长为6πcm,
∴侧面展开扇形的弧长为6πcm,
设扇形的半径为r,
∵圆锥的侧面展开图的圆心角是120°,
∴=6π,
解得:r=9,
∴侧面积为×6π×9=27π(cm2),
故答案为:27πcm2.
21.解:设圆锥的底面半径为r.
由题意,2π?r=,
∴r=2,
故答案为:2.
22.解:由题意知:弧长=圆锥底面周长=2×4π=8π(厘米),
设所求圆心角的度数为n°,
则=8π,解得n=160,
即侧面展开扇形图的圆心角为160°.
故答案为:160°.
23.解:设这个圆柱的高是xcm,圆锥和圆柱的底面积都为S,
根据题意得S?x=9××S×8.1,
解得x=24.3(cm),
即这个圆柱的高是24.3cm.
故答案为24.3.
24.解:设圆柱体的高为h,
∵圆柱体侧面积为24π,底面圆的半径等于3,
∴2π×3×h=24π,
解得:h=4,
故答案为:4.
25.解:侧面积=2×3.14×3.2×5=100.48(dm2).
故这个圆柱的侧面积为100.48dm2.
故答案为:100.48.
三.解答题
26.解:(1)圆锥的体积=×π×52×2.5=π≈60.25(立方米),
答:这堆沙子约有60.25立方米;
(2)用这堆沙子在10m宽的公路上铺2cm厚的路面,能铺的米数为:60.25÷(10×0.02)=301.25(米),
答:用这堆沙子在10m宽的公路上铺2cm厚的路面,能铺301.25米;
(3)压路机一分钟压的面积=π×1×2×6≈36(平方米),
则这台压路机压一遍这段路面大约需要的时间=301.25×10÷36≈84(分).
27.解:(1)如图2中,作SE⊥AF交弧AF于C.
设图2中的扇形的圆心角为n°,
根据题意得=2π?1,
∴n=90°,
∵SA=SF,
∴△SFA是等腰直角三角形,
∴AF=SF=4,SE=AF=2,
∴S阴=S扇形SAF﹣S△SAF=﹣××=4π﹣8;
(2)在图2中,∵SC是一条蜜糖线,AE⊥SC,AE=2,
∴一只蚂蚁从A沿着圆锥表面最少需要爬2个单位长度才能吃到蜜糖.
28.解:(1)BC=(36﹣2x)=(18﹣x)cm,
旋转形成的圆柱的底面圆的周长为2π(18﹣x)cm.
故答案为:(18﹣x),2π(18﹣x).
(2)S=2π(18﹣x)?x=﹣2πx2+36πx(0<x<18).
(3)∵S=﹣2πx2+36πx=﹣2π(x﹣9)2+162π,
又∵﹣2π<0,
∴x=9时,S有最大值.
(4)由题意:﹣2πx2+36πx=18π,
∴x2﹣18x+9=0,
解得x=9+6或9﹣6(舍弃),
∴矩形的长是(9+6)cm,宽是(9﹣6)cm.
故答案为:(9+6),(9﹣6).
29.解:(1)由题意和函数图象可得,
圆柱容器的高为12cm,
故答案为:12;
(2)BC过点(26,8),(42,12),
设线段BC所对应的函数表达式为h=kt+b,
将点(26,8),(42,12)代入,得
,
解得,
所以线段BC所对应的函数表达式为h=t+;
(3)以为“柱锥体”的高为:5+3=8(cm),
所以顶端距离水面3.5cm位置有2个,
①当h=8﹣3.5=4.5时,在OA上,
设OA解析式为h=kt,过点A(15,5),
所以15k=5,解得k=,
所以OA解析式为h=t,
当h=4.5时,t=13.5;
②当h=8+3.5=11.5时,在BC上,
将h=11.5代入h=t+,
解得t=40.
综上所述:“柱锥体”顶端距离水面3.5cm时t的值为13.5s或40s.
30.解:(1)由题意3×2πr=,
∴r=4.
(2)圆锥的表面积=π?42+?2π?4?16=80π.
