2020——2021学年人教版 八年级数学下册 第十八章 平行四边形 培优训练(word版含解析)
文档属性
| 名称 | 2020——2021学年人教版 八年级数学下册 第十八章 平行四边形 培优训练(word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 521.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-16 00:00:00 | ||
图片预览


文档简介
人教版 八年级下册 第十八章 平行四边形 培优训练
一、选择题
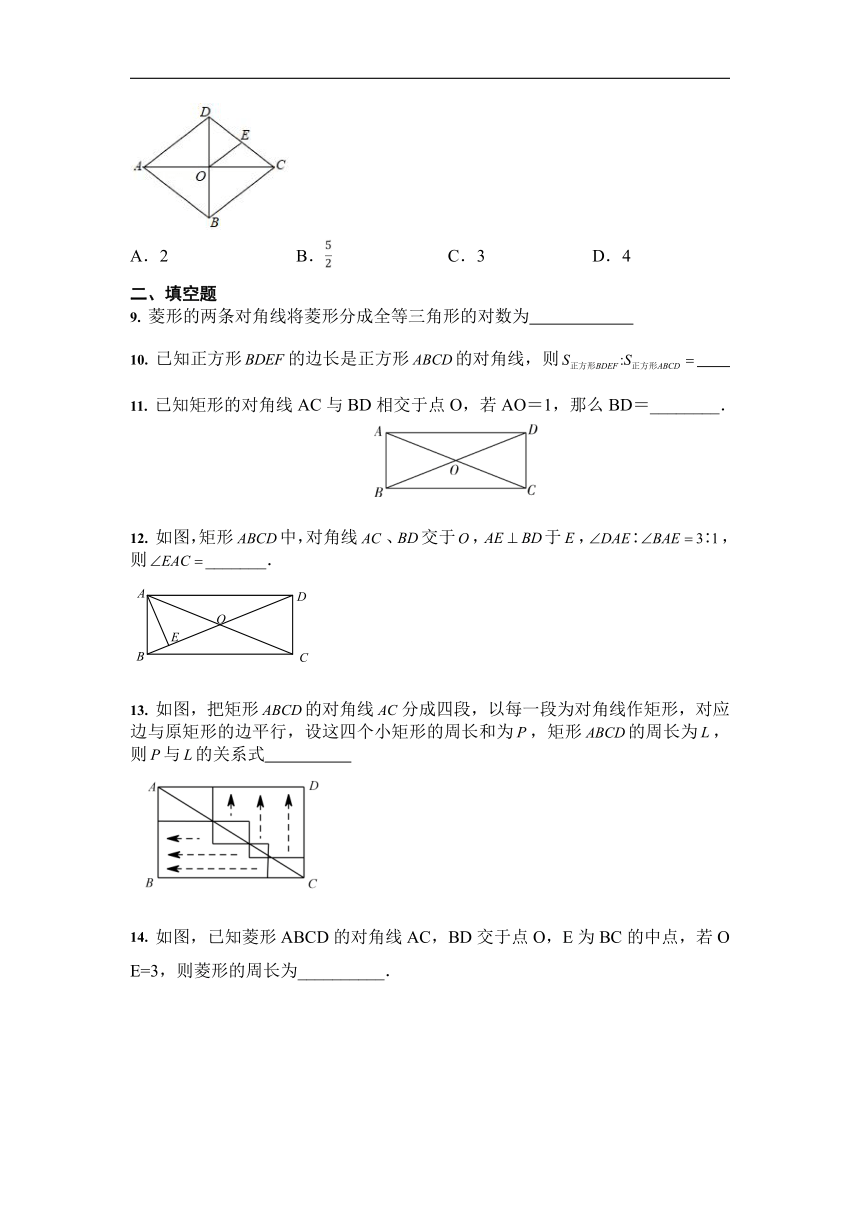
1. (2020·绥化)如图,四边形ABCD是菱形,E、F分别是BC、CD两边上的点,不能保证△ABE和△ADF一定全等的条件是( )
A.∠BAF=∠DAE B.EC=FC C.AE=AF D.BE=DF
2. 如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边的正方形EFGH的周长为( )
A.
B. 2
C. +1
D. 2+1
3. 菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=,BD=2,则菱形ABCD的面积为( )
A. 2 B. 4 C. 6 D. 8
4. 如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是( )
A. 7 B. 9 C. 10 D. 11
5. 在平行四边形中,点、、、和、、、分别为和的五等分点,点、和、分别是和的三等分点,已知四边形的面积为,则平行四边形面积为( )
A.2 B. C. D.
6. 如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH,若BE∶EC=2∶1,则线段CH的长是( )
A. 3 B. 4 C. 5 D. 6
7. 如图,在矩形ABCD中,点E,F在对角线BD.请添加一个条件,使得结论“AE=CF”成立,并加以证明.
8. (3分)如图,四边形ABCD是菱形,对角线AC,BD相交于点O,AC=8.BD=6,点E是CD上一点,连接OE,若OE=CE,则OE的长是( )
A.2 B. C.3 D.4
二、填空题
9. 菱形的两条对角线将菱形分成全等三角形的对数为
10. 已知正方形的边长是正方形的对角线,则
11. 已知矩形的对角线AC与BD相交于点O,若AO=1,那么BD=________.
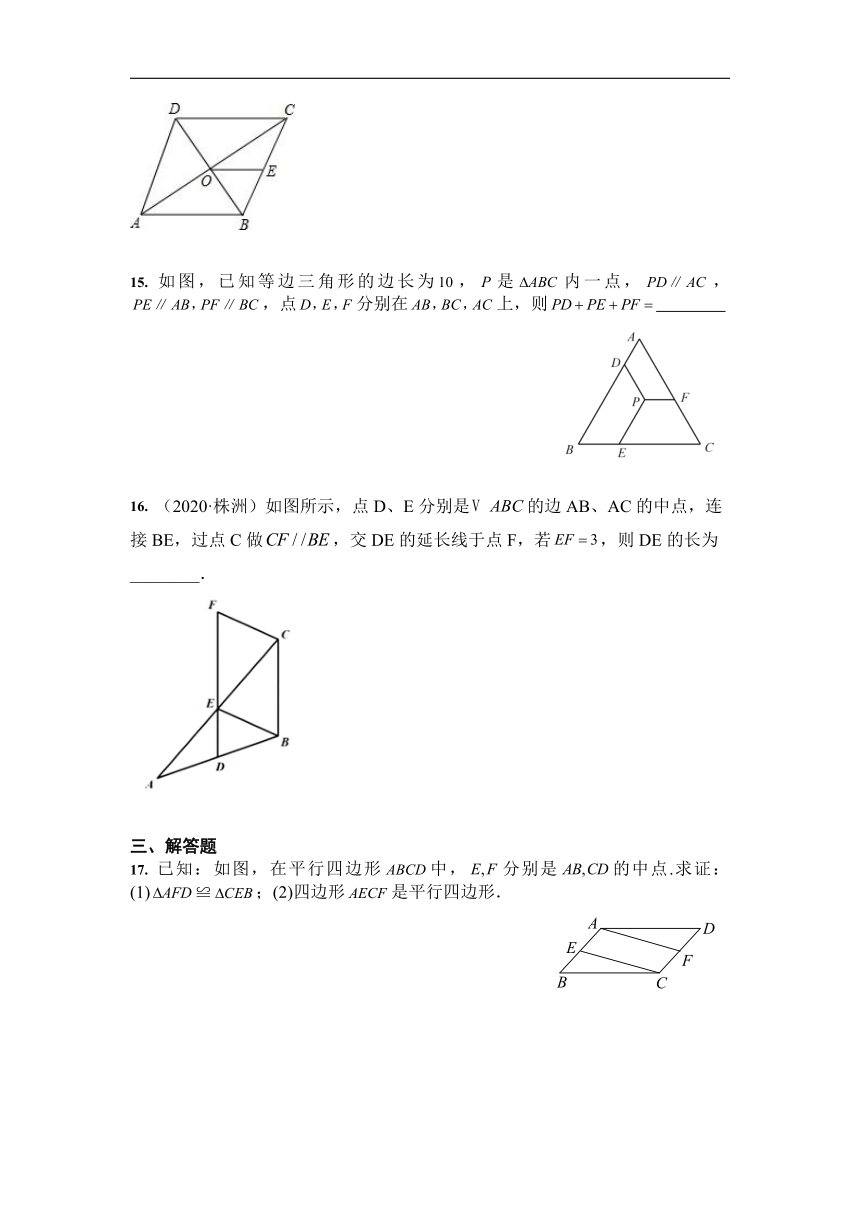
12. 如图,矩形中,对角线、交于,于,,则_______.
13. 如图,把矩形的对角线分成四段,以每一段为对角线作矩形,对应边与原矩形的边平行,设这四个小矩形的周长和为,矩形的周长为,则与的关系式
14. 如图,已知菱形ABCD的对角线AC,BD交于点O,E为BC的中点,若OE=3,则菱形的周长为__________.
15. 如图,已知等边三角形的边长为,是内一点,,,点分别在上,则
16. (2020·株洲)如图所示,点D、E分别是的边AB、AC的中点,连接BE,过点C做,交DE的延长线于点F,若,则DE的长为________.
三、解答题
17. 已知:如图,在平行四边形中,分别是的中点.求证:(1)≌;(2)四边形是平行四边形.
18. 如图,在平行四边形中,是的中点,且,
求证:四边形是矩形.
19. 如图所示,在长方形中,点是边的中点,点是边的中点,与交于点.若,求的度数.
20. 如图⑴,四边形中,若,则必然等于.请运用结论证明下述问题:如图⑵,在平行四边形中取一点,使得,求证:.
人教版 八年级下册 第十八章 平行四边形 培优训练-答案
一、选择题
1. 【答案】C
【解析】由菱形的性质可知AB=AD,∠B=∠D,因此△ABE与△ADF已具备了一边一角相等.当选项A做条件时可用“ASA”判定全等;当选项B或选项D做条件时,可用“SAS”判定全等.选项C做条件时是“边、边、角”,不能判定两个三角形全等.故选C.
2. 【答案】B 【解析】∵正方形ABCD的面积为1,∴BC=CD=1,∵E、F是边的中点,∴CE=CF=,∴EF==,则正方形EFGH的周长为4×=2.
3. 【答案】A 【解析】∵E,F 分别是 AD,CD 边上的中点,即EF是△ACD的中位线,∴AC=2EF=2,则菱形ABCD的面积=AC·BD=×2×2=2.
4. 【答案】D 【解析】本题考查勾股定理、三角形的中位线定理和四边形的周长 . 解题思路:
?四边形EFGH的周长=EF+FG+HG+EH=11.
5. 【答案】C
6. 【答案】B 【解析】设CH=x,∵BE∶EC=2∶1,BC=9,∴EC=3,由折叠可知,EH=DH=9-x,在Rt△ECH中,由勾股定理得:(9-x)2=32+x2,解得:x=4.
7. 【答案】添加的条件是BE=DF(答案不唯一).
证明:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,
∴∠ABD=∠BDC,
又∵BE=DF(添加),
∴△ABE≌△CDF(SAS),
∴AE=CF.
8. 【答案】B
【解析】根据菱形的对角线互相垂直平分求出OB,OC,AC⊥BD,然后利用勾股定理列式求出BC,最后根据三角形的中位线平行于第三边并且等于第三边的一半求解即可.
∵菱形ABCD的对角线AC、BD相交于点O,
∴OBBD6=3,OA=OCAC8=4,AC⊥BD,
由勾股定理得,BC5,
∴AD=5,
∵OE=CE,
∴∠DCA=∠EOC,
∵四边形ABCD是菱形,
∴∠DCA=∠DAC,
∴∠DAC=∠EOC,
∴OE∥AD,
∵AO=OC,
∴OE是△ADC的中位线,
∴OEAD=2.5.
二、填空题
9. 【答案】
【解析】根据菱形的性质可知:共有对
10. 【答案】
11. 【答案】2 【解析】根据“矩形的对角线相等且互相平分”进行解题便可.∵四边形ABCD是矩形,∴BD=AC=2OA,∵OA=1,∴BD=2.
12. 【答案】
【解析】∵
∴,
∵,∴.
13. 【答案】.
【解析】如图,将四个小矩形的边分别向外平移,正好拼接成矩形的四边,所以
14. 【答案】24
【解析】∵四边形ABCD是菱形,
∴AB=BC=CD=AD,BO=DO,
∵点E是BC的中点,
∴OE是△BCD的中位线,
∴CD=2OE=2×3=6,
∴菱形ABCD的周长=4×6=24;
故答案为:24.
15. 【答案】
16. 【答案】
【解析】先证明DE为的中位线,得到四边形BCFE为平行四边形,求出BC=EF=3,根据中位线定理即可求解.
∵D、E分别是的边AB、AC的中点,
∴DE为的中位线,
∴DE∥BC,,
∵,
∴四边形BCFE为平行四边形,
∴BC=EF=3,
∴.
故答案为:
三、解答题
17. 【答案】
(1)∵四边形平行四边形,
∴.
又∵分别是的中点,
∴.
∴.
∴≌.
(2)由(1)知,≌. ∴.
∴四边形是平行四边形.
18. 【答案】
∵四边形是平行四边形,∴,
∵是的中点,∴
在和中
∴≌ (),∴
∴,∴四边形是矩形
19. 【答案】
如图所示,将平移至,此时为的中点.
连接,则,
故.
由于,,
故.
20. 【答案】
分别过点、作,,交于点,连接.
∵,
∴,,,
∵,,∴,
∴为平行四边形,∴
∵,∴≌,∴
在四边形中,
∴,∴
一、选择题
1. (2020·绥化)如图,四边形ABCD是菱形,E、F分别是BC、CD两边上的点,不能保证△ABE和△ADF一定全等的条件是( )
A.∠BAF=∠DAE B.EC=FC C.AE=AF D.BE=DF
2. 如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边的正方形EFGH的周长为( )
A.
B. 2
C. +1
D. 2+1
3. 菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=,BD=2,则菱形ABCD的面积为( )
A. 2 B. 4 C. 6 D. 8
4. 如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是( )
A. 7 B. 9 C. 10 D. 11
5. 在平行四边形中,点、、、和、、、分别为和的五等分点,点、和、分别是和的三等分点,已知四边形的面积为,则平行四边形面积为( )
A.2 B. C. D.
6. 如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH,若BE∶EC=2∶1,则线段CH的长是( )
A. 3 B. 4 C. 5 D. 6
7. 如图,在矩形ABCD中,点E,F在对角线BD.请添加一个条件,使得结论“AE=CF”成立,并加以证明.
8. (3分)如图,四边形ABCD是菱形,对角线AC,BD相交于点O,AC=8.BD=6,点E是CD上一点,连接OE,若OE=CE,则OE的长是( )
A.2 B. C.3 D.4
二、填空题
9. 菱形的两条对角线将菱形分成全等三角形的对数为
10. 已知正方形的边长是正方形的对角线,则
11. 已知矩形的对角线AC与BD相交于点O,若AO=1,那么BD=________.
12. 如图,矩形中,对角线、交于,于,,则_______.
13. 如图,把矩形的对角线分成四段,以每一段为对角线作矩形,对应边与原矩形的边平行,设这四个小矩形的周长和为,矩形的周长为,则与的关系式
14. 如图,已知菱形ABCD的对角线AC,BD交于点O,E为BC的中点,若OE=3,则菱形的周长为__________.
15. 如图,已知等边三角形的边长为,是内一点,,,点分别在上,则
16. (2020·株洲)如图所示,点D、E分别是的边AB、AC的中点,连接BE,过点C做,交DE的延长线于点F,若,则DE的长为________.
三、解答题
17. 已知:如图,在平行四边形中,分别是的中点.求证:(1)≌;(2)四边形是平行四边形.
18. 如图,在平行四边形中,是的中点,且,
求证:四边形是矩形.
19. 如图所示,在长方形中,点是边的中点,点是边的中点,与交于点.若,求的度数.
20. 如图⑴,四边形中,若,则必然等于.请运用结论证明下述问题:如图⑵,在平行四边形中取一点,使得,求证:.
人教版 八年级下册 第十八章 平行四边形 培优训练-答案
一、选择题
1. 【答案】C
【解析】由菱形的性质可知AB=AD,∠B=∠D,因此△ABE与△ADF已具备了一边一角相等.当选项A做条件时可用“ASA”判定全等;当选项B或选项D做条件时,可用“SAS”判定全等.选项C做条件时是“边、边、角”,不能判定两个三角形全等.故选C.
2. 【答案】B 【解析】∵正方形ABCD的面积为1,∴BC=CD=1,∵E、F是边的中点,∴CE=CF=,∴EF==,则正方形EFGH的周长为4×=2.
3. 【答案】A 【解析】∵E,F 分别是 AD,CD 边上的中点,即EF是△ACD的中位线,∴AC=2EF=2,则菱形ABCD的面积=AC·BD=×2×2=2.
4. 【答案】D 【解析】本题考查勾股定理、三角形的中位线定理和四边形的周长 . 解题思路:
?四边形EFGH的周长=EF+FG+HG+EH=11.
5. 【答案】C
6. 【答案】B 【解析】设CH=x,∵BE∶EC=2∶1,BC=9,∴EC=3,由折叠可知,EH=DH=9-x,在Rt△ECH中,由勾股定理得:(9-x)2=32+x2,解得:x=4.
7. 【答案】添加的条件是BE=DF(答案不唯一).
证明:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,
∴∠ABD=∠BDC,
又∵BE=DF(添加),
∴△ABE≌△CDF(SAS),
∴AE=CF.
8. 【答案】B
【解析】根据菱形的对角线互相垂直平分求出OB,OC,AC⊥BD,然后利用勾股定理列式求出BC,最后根据三角形的中位线平行于第三边并且等于第三边的一半求解即可.
∵菱形ABCD的对角线AC、BD相交于点O,
∴OBBD6=3,OA=OCAC8=4,AC⊥BD,
由勾股定理得,BC5,
∴AD=5,
∵OE=CE,
∴∠DCA=∠EOC,
∵四边形ABCD是菱形,
∴∠DCA=∠DAC,
∴∠DAC=∠EOC,
∴OE∥AD,
∵AO=OC,
∴OE是△ADC的中位线,
∴OEAD=2.5.
二、填空题
9. 【答案】
【解析】根据菱形的性质可知:共有对
10. 【答案】
11. 【答案】2 【解析】根据“矩形的对角线相等且互相平分”进行解题便可.∵四边形ABCD是矩形,∴BD=AC=2OA,∵OA=1,∴BD=2.
12. 【答案】
【解析】∵
∴,
∵,∴.
13. 【答案】.
【解析】如图,将四个小矩形的边分别向外平移,正好拼接成矩形的四边,所以
14. 【答案】24
【解析】∵四边形ABCD是菱形,
∴AB=BC=CD=AD,BO=DO,
∵点E是BC的中点,
∴OE是△BCD的中位线,
∴CD=2OE=2×3=6,
∴菱形ABCD的周长=4×6=24;
故答案为:24.
15. 【答案】
16. 【答案】
【解析】先证明DE为的中位线,得到四边形BCFE为平行四边形,求出BC=EF=3,根据中位线定理即可求解.
∵D、E分别是的边AB、AC的中点,
∴DE为的中位线,
∴DE∥BC,,
∵,
∴四边形BCFE为平行四边形,
∴BC=EF=3,
∴.
故答案为:
三、解答题
17. 【答案】
(1)∵四边形平行四边形,
∴.
又∵分别是的中点,
∴.
∴.
∴≌.
(2)由(1)知,≌. ∴.
∴四边形是平行四边形.
18. 【答案】
∵四边形是平行四边形,∴,
∵是的中点,∴
在和中
∴≌ (),∴
∴,∴四边形是矩形
19. 【答案】
如图所示,将平移至,此时为的中点.
连接,则,
故.
由于,,
故.
20. 【答案】
分别过点、作,,交于点,连接.
∵,
∴,,,
∵,,∴,
∴为平行四边形,∴
∵,∴≌,∴
在四边形中,
∴,∴
