10.3 解二元一次方程组(第2课时)(共38张PPT)
文档属性
| 名称 | 10.3 解二元一次方程组(第2课时)(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 00:00:00 | ||
图片预览











文档简介
第2课时
10.3 解二元一次方程组
第10章 二元一次方程
2020-2021学年度苏科版七年级下册
温故而知新
1、用含x的代数式表示y :
(1) x + y = 22
(2)5 x =2 y
(3)2 x - y =5
2、用含y 的代数式表示x :2 x - 7 y = 8
y= 22- x
y = x
2
5
y = 2x -5
x =
2
7y+8
回顾与思考
NBA篮球联赛中每场比赛都要分出胜负,若每队胜一场得2分,负一场得1分.如果火箭队为争取较好名次,想在最后22场比赛中得40分,求它的胜、负场数应分别是多少?
解:设胜x场,负y场,依题意得
③是一元一次方程,相信大家都会解.那么
根据上面的提示,你会解这个方程组吗?
再将②中的y转换为(22- x)就得到了③
解:设胜x场,则负场有(22-x)场,依题意得
比较一下上面的方程组与方程有什么关系?
③
40
)
22
(
2
=
-
+
x
x
①
②
22
=
+
y
x
40
2
=
+
y
x
由①我们可以得到:
x
y
-
=
22
二元一次方程组中有两个未知数,
如果消去其中一个未知数,将二元一次方
程组转化为我们熟悉的一元一次方程,我
们就可以先解出一个未知数,然后再设法
求另一个未知数.这种将未知数的个数由多
化少、逐一解决的思想,叫做消元思想.
请同学们读一读:
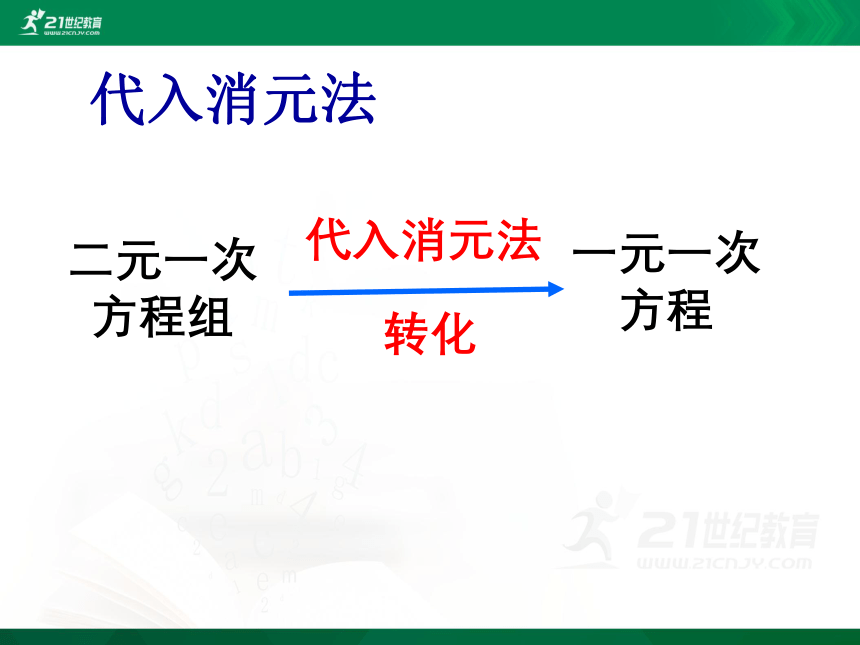
代入消元法
二元一次方程组
代入消元法
转化
一元一次方程
例1 解方程组:
解:
①
②
x +y = 12,
2x +y = 20.
由 ①得:
y = 12 –x.
③
把③代入②得:
2x +12-x= 20.
解这个一元一次方程,得
x = 5.
把x =8代入③,得
y =
4.
所以原方程组的解是
x = 8,
y = 4.
用代入法解二元一次方程组的一般步骤
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,求得另一个未知数的值;
4、写出方程组的解.
变
代
求
写
说说方法:
1、解方程组:
解:
①
②
x +y = 7,
3x +y = 17.
由 ①得:
y = 7 –x.
③
把③代入②得:
3x +7-x= 17.
解得 x = 5.
把x =5代入③,得
y =
2.
∴
x = 5,
y = 2.
2、 解方程组
解:
①
②
2x -7y = 8,
3x-y -10= 0.
由 ①得:
x = 4+ y.
③
把③代入②得:
3(4+ y) -8y-10= 0.
解得 y = -0.8.
把y = -0.8代入③,得
x =4+ ×(-0.8),
即 x=1.2.
∴
x = 1.2,
y = -0.8.
用代入法解方程组
2x+3y=16 ①
x+4y=13 ②
解:
∴原方程组的解是
x=5
y=2
(在实践中学习探究)
由② ,得 x=13 - 4y ③
把③代入① ,得
2(13 - 4y)+3y=16
26 –8y +3y =16
-5y= -10
y=2
把y=2代入③ ,得 x=5
把③代入②可以吗?试试看
把y=2代入① 或②可以吗?
把求出的解代入原方程组,可以检验你得到的解对不对.
随堂练习:
⑴
y =2 x
x+ y =12
⑵
x=—
y -5
2
4 x +3 y =65
⑶
x + y =11
x- y =7
⑷
3 x -2 y =9
x+2 y =3
x =4
y =8
x =5
y =15
x =3
y =0
用代入消元法解下列方程组:
x =9
y =2
能 力 检 测
(1)
(2)
b=2
ì
í
?
a=8
y=-1
ì
í
?
x=2
用代入法解二元一次方程组:
(3)
(4)
y=5
ì
í
?
x=3
y=1
ì
í
?
x=5
1、二元一次方程组
代入消元法
一元一次方程
2、代入消元法的一般步骤:
3、思想方法:转化思想、消元思想、
方程(组)思想.
知 识 梳 理
变
代
求
写
转化
解下面的二元一次方程组
代入①,消去 了!
把②变形得:
标准的代入消元法
②
①
还有别的方法吗?
认真观察此方程组中各个未知数
的系数有什么特点,并分组讨论看
还有没有其它的解法,并尝试一下能
否求出它的解.
新思路 新体验
①
②
和
互为相反数……
分析:
①
②
3x+5y +2x - 5y=10
①左边 + ② 左边 = ① 右边 + ②右边
5x =10
x=2
(3x + 5y)+(2x - 5y)= 21 + (-11)
等式性质
②
①
①
②
① + ②
① - ②
思考
联系上面的解法,想一想怎样解方程组
感悟规律 揭示本质
两个二元一次方程中同一未知数的系数相反或相等时,将两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称加减法.
2x-5y=7 ①
2x+3y=-1 ②
观察方程组中的两个方程,未知数x的系数相等,都是2.把两个方程两边分别相减,就可以消去未知数x,同样得到一个一元一次方程.
分析:
举一反三
解方程组
2x-5y=7 ①
2x+3y=-1 ②
解:把 ②-①得: 8y=-8
y=-1
把y =-1代入①,得:
2x-5×(-1)=7
解得:x=1
所以原方程组的解是
x=1
y=-1
举一反三
解方程组:
①
②
解:①+②,得
7y=14,
即,x=2.
把x=2代人①,得
6+7y=9.
解得
所以
3x-2y= -1 ①
6x+7y=9 ②
运用新知 拓展创新
分析:
1、要想用加减法解二元一次方程组
必须具备什么条件?
2、此方程组能否直接用加减法消元?
例2 解方程组:
①
②
解:由①+②,得
4x=6,
把 代入①,得
所以原方程的解是
例3 解方程组:
①
②
解:①×3,得
15x-6y=12.
③-④,得
所以原方程的解是
③
②×2,得
4x-6y=-10.
④
11x=22.
x=2.
将x=2代入①,得
5×2-2y=4.
y=3.
用加减法解方程组:
解:
①×3得 6x+9y=36 ③
所以原方程组的解是
①
②
③-④得: y=2
把y =2代入①,
解得: x=3
②×2得 6x+8y=34 ④
用加减法先消去未知数y该如何解?解得的结果与左面的解相同吗?
用代入消元法解下列方程组:
(1)
y=x,
y+4x=15;
{
(3)
x-7y =0,
x-9y+8 =0;
{
(4)
x-y =3,
x+y =5.
{
(2)
x+2y=4 ,
2x-3y=1;
{
解:将①代入②,得x+4x=15,
x=3.
将x=3代入①,得y=3.
所以原方程的解是
x=3,
y=3.
{
①
②
(1)
y=x,
y+4x=15;
{
①
②
解:将①代入②,得2×(4-2y)-3y=1,
y=1.
将y=1代入①,得x=2.
所以原方程的解是
x=2,
y=1.
{
(2)
x+2y=4 ,
2x-3y=1;
{
①
②
解:由①,得 x=7y ,
将③代入②,得7y-9y +8=0,
y=4.
将y=4代入③,得x=28.
所以原方程的解是
x=28,
y=4.
{
③
(3)
x-7y =0,
x-9y+8 =0;
{
①
②
解:由②,得x=5-y ,
将③代入①,得5-y -y=3,
y=1.
将y=1代入③,得x=4.
所以原方程的解是
x=4,
y=1.
{
③
(4)
x-y =3,
x+y =5.
{
解下列方程组:
(1)
2x+y=32,
2x-y=0;
{
(3)
6x+5z =25,
3+4z =20;
{
(4)
3s+4t =7,
3t-2s =1.
{
(2)
3x-y=-4,
x-2y=-3;
{
解:①+②,得4x=32,
x=8.
将x=8代入①,得y=16.
所以原方程的解是
x=8 ,
y=16.
{
①
②
(1)
{
2x+y=32,
2x-y=0;
解:②-①×2 ,得 -5x=5,
x=-1.
将x=-1代入② ,得 y=1.
所以原方程的解是
x=-1 ,
y=1.
{
①
②
(2)
{
3x-y=-4,
x-2y=-3;
解:①-②×2 ,得-3z =-15 ,
z =5.
将z =5代入② ,得 x=0.
所以原方程的解是
x=0 ,
z=5.
{
①
②
(3)
{
6x+5z =25,
3x+4z =20;
解:①×2 +②×3 ,得17t =17 ,
t=1.
将t=1代入② ,得s=1.
所以原方程的解是
t=1 ,
s=1.
{
①
②
(4)
{
3s+4t =7,
3t-2s =1.
基本思路:
主要步骤:
加减消元:
二元
一元
加减
消去一个元
求解
分别求出两个未知数的值
加减消元法解方程组基本思路是什么?主要步骤有哪些?
变形
同一个未知数的系
数相同或互为相反数
写解
写出方程组的解
谢谢聆听
10.3 解二元一次方程组
第10章 二元一次方程
2020-2021学年度苏科版七年级下册
温故而知新
1、用含x的代数式表示y :
(1) x + y = 22
(2)5 x =2 y
(3)2 x - y =5
2、用含y 的代数式表示x :2 x - 7 y = 8
y= 22- x
y = x
2
5
y = 2x -5
x =
2
7y+8
回顾与思考
NBA篮球联赛中每场比赛都要分出胜负,若每队胜一场得2分,负一场得1分.如果火箭队为争取较好名次,想在最后22场比赛中得40分,求它的胜、负场数应分别是多少?
解:设胜x场,负y场,依题意得
③是一元一次方程,相信大家都会解.那么
根据上面的提示,你会解这个方程组吗?
再将②中的y转换为(22- x)就得到了③
解:设胜x场,则负场有(22-x)场,依题意得
比较一下上面的方程组与方程有什么关系?
③
40
)
22
(
2
=
-
+
x
x
①
②
22
=
+
y
x
40
2
=
+
y
x
由①我们可以得到:
x
y
-
=
22
二元一次方程组中有两个未知数,
如果消去其中一个未知数,将二元一次方
程组转化为我们熟悉的一元一次方程,我
们就可以先解出一个未知数,然后再设法
求另一个未知数.这种将未知数的个数由多
化少、逐一解决的思想,叫做消元思想.
请同学们读一读:
代入消元法
二元一次方程组
代入消元法
转化
一元一次方程
例1 解方程组:
解:
①
②
x +y = 12,
2x +y = 20.
由 ①得:
y = 12 –x.
③
把③代入②得:
2x +12-x= 20.
解这个一元一次方程,得
x = 5.
把x =8代入③,得
y =
4.
所以原方程组的解是
x = 8,
y = 4.
用代入法解二元一次方程组的一般步骤
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,求得另一个未知数的值;
4、写出方程组的解.
变
代
求
写
说说方法:
1、解方程组:
解:
①
②
x +y = 7,
3x +y = 17.
由 ①得:
y = 7 –x.
③
把③代入②得:
3x +7-x= 17.
解得 x = 5.
把x =5代入③,得
y =
2.
∴
x = 5,
y = 2.
2、 解方程组
解:
①
②
2x -7y = 8,
3x-y -10= 0.
由 ①得:
x = 4+ y.
③
把③代入②得:
3(4+ y) -8y-10= 0.
解得 y = -0.8.
把y = -0.8代入③,得
x =4+ ×(-0.8),
即 x=1.2.
∴
x = 1.2,
y = -0.8.
用代入法解方程组
2x+3y=16 ①
x+4y=13 ②
解:
∴原方程组的解是
x=5
y=2
(在实践中学习探究)
由② ,得 x=13 - 4y ③
把③代入① ,得
2(13 - 4y)+3y=16
26 –8y +3y =16
-5y= -10
y=2
把y=2代入③ ,得 x=5
把③代入②可以吗?试试看
把y=2代入① 或②可以吗?
把求出的解代入原方程组,可以检验你得到的解对不对.
随堂练习:
⑴
y =2 x
x+ y =12
⑵
x=—
y -5
2
4 x +3 y =65
⑶
x + y =11
x- y =7
⑷
3 x -2 y =9
x+2 y =3
x =4
y =8
x =5
y =15
x =3
y =0
用代入消元法解下列方程组:
x =9
y =2
能 力 检 测
(1)
(2)
b=2
ì
í
?
a=8
y=-1
ì
í
?
x=2
用代入法解二元一次方程组:
(3)
(4)
y=5
ì
í
?
x=3
y=1
ì
í
?
x=5
1、二元一次方程组
代入消元法
一元一次方程
2、代入消元法的一般步骤:
3、思想方法:转化思想、消元思想、
方程(组)思想.
知 识 梳 理
变
代
求
写
转化
解下面的二元一次方程组
代入①,消去 了!
把②变形得:
标准的代入消元法
②
①
还有别的方法吗?
认真观察此方程组中各个未知数
的系数有什么特点,并分组讨论看
还有没有其它的解法,并尝试一下能
否求出它的解.
新思路 新体验
①
②
和
互为相反数……
分析:
①
②
3x+5y +2x - 5y=10
①左边 + ② 左边 = ① 右边 + ②右边
5x =10
x=2
(3x + 5y)+(2x - 5y)= 21 + (-11)
等式性质
②
①
①
②
① + ②
① - ②
思考
联系上面的解法,想一想怎样解方程组
感悟规律 揭示本质
两个二元一次方程中同一未知数的系数相反或相等时,将两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称加减法.
2x-5y=7 ①
2x+3y=-1 ②
观察方程组中的两个方程,未知数x的系数相等,都是2.把两个方程两边分别相减,就可以消去未知数x,同样得到一个一元一次方程.
分析:
举一反三
解方程组
2x-5y=7 ①
2x+3y=-1 ②
解:把 ②-①得: 8y=-8
y=-1
把y =-1代入①,得:
2x-5×(-1)=7
解得:x=1
所以原方程组的解是
x=1
y=-1
举一反三
解方程组:
①
②
解:①+②,得
7y=14,
即,x=2.
把x=2代人①,得
6+7y=9.
解得
所以
3x-2y= -1 ①
6x+7y=9 ②
运用新知 拓展创新
分析:
1、要想用加减法解二元一次方程组
必须具备什么条件?
2、此方程组能否直接用加减法消元?
例2 解方程组:
①
②
解:由①+②,得
4x=6,
把 代入①,得
所以原方程的解是
例3 解方程组:
①
②
解:①×3,得
15x-6y=12.
③-④,得
所以原方程的解是
③
②×2,得
4x-6y=-10.
④
11x=22.
x=2.
将x=2代入①,得
5×2-2y=4.
y=3.
用加减法解方程组:
解:
①×3得 6x+9y=36 ③
所以原方程组的解是
①
②
③-④得: y=2
把y =2代入①,
解得: x=3
②×2得 6x+8y=34 ④
用加减法先消去未知数y该如何解?解得的结果与左面的解相同吗?
用代入消元法解下列方程组:
(1)
y=x,
y+4x=15;
{
(3)
x-7y =0,
x-9y+8 =0;
{
(4)
x-y =3,
x+y =5.
{
(2)
x+2y=4 ,
2x-3y=1;
{
解:将①代入②,得x+4x=15,
x=3.
将x=3代入①,得y=3.
所以原方程的解是
x=3,
y=3.
{
①
②
(1)
y=x,
y+4x=15;
{
①
②
解:将①代入②,得2×(4-2y)-3y=1,
y=1.
将y=1代入①,得x=2.
所以原方程的解是
x=2,
y=1.
{
(2)
x+2y=4 ,
2x-3y=1;
{
①
②
解:由①,得 x=7y ,
将③代入②,得7y-9y +8=0,
y=4.
将y=4代入③,得x=28.
所以原方程的解是
x=28,
y=4.
{
③
(3)
x-7y =0,
x-9y+8 =0;
{
①
②
解:由②,得x=5-y ,
将③代入①,得5-y -y=3,
y=1.
将y=1代入③,得x=4.
所以原方程的解是
x=4,
y=1.
{
③
(4)
x-y =3,
x+y =5.
{
解下列方程组:
(1)
2x+y=32,
2x-y=0;
{
(3)
6x+5z =25,
3+4z =20;
{
(4)
3s+4t =7,
3t-2s =1.
{
(2)
3x-y=-4,
x-2y=-3;
{
解:①+②,得4x=32,
x=8.
将x=8代入①,得y=16.
所以原方程的解是
x=8 ,
y=16.
{
①
②
(1)
{
2x+y=32,
2x-y=0;
解:②-①×2 ,得 -5x=5,
x=-1.
将x=-1代入② ,得 y=1.
所以原方程的解是
x=-1 ,
y=1.
{
①
②
(2)
{
3x-y=-4,
x-2y=-3;
解:①-②×2 ,得-3z =-15 ,
z =5.
将z =5代入② ,得 x=0.
所以原方程的解是
x=0 ,
z=5.
{
①
②
(3)
{
6x+5z =25,
3x+4z =20;
解:①×2 +②×3 ,得17t =17 ,
t=1.
将t=1代入② ,得s=1.
所以原方程的解是
t=1 ,
s=1.
{
①
②
(4)
{
3s+4t =7,
3t-2s =1.
基本思路:
主要步骤:
加减消元:
二元
一元
加减
消去一个元
求解
分别求出两个未知数的值
加减消元法解方程组基本思路是什么?主要步骤有哪些?
变形
同一个未知数的系
数相同或互为相反数
写解
写出方程组的解
谢谢聆听
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
