5.1.2 垂线同步练习(含解析)
图片预览

文档简介
人教版数学七年级下册 第五章 相交线与平行线 5.1.2 垂线 同步练习
一、单选题
1.若线段 , 分别是 边上的高线和中线,则(?? )
A.?????????????????????????B.?????????????????????????C.?????????????????????????D.?
2.如图,连接直线 外一点 与直线 上各点 , ,其中 ,这些线段 , , , , 中,最短的线段是(?? )
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
3.如图,AC⊥BC,AC=4.5,若点P在直线BC上,则AP的长可能是(??? ).
A.?5???????????????????????????????????????????B.?4???????????????????????????????????????????C.?3???????????????????????????????????????????D.?2
4.如图,把河 中的水引到村庄C拟修水渠中最短的是(? )
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
5.如图,在平面内作已知直线m的垂线,可作垂线的条数有(??? )
A.?0条?????????????????????????????????????B.?1条?????????????????????????????????????C.?2条?????????????????????????????????????D.?无数条
6.如图,直线 , 相交于点O, ,垂足为点O.若 ,则 的度数为(?? )
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
7.在同-平面内,若∠A与∠B的两边分别垂直,且∠A比∠B的3倍少40°,则∠A的度数为(??? )
A.?20°????????????????????????????????B.?55°????????????????????????????????C.?20°或 125°????????????????????????????????D.?20°或55°
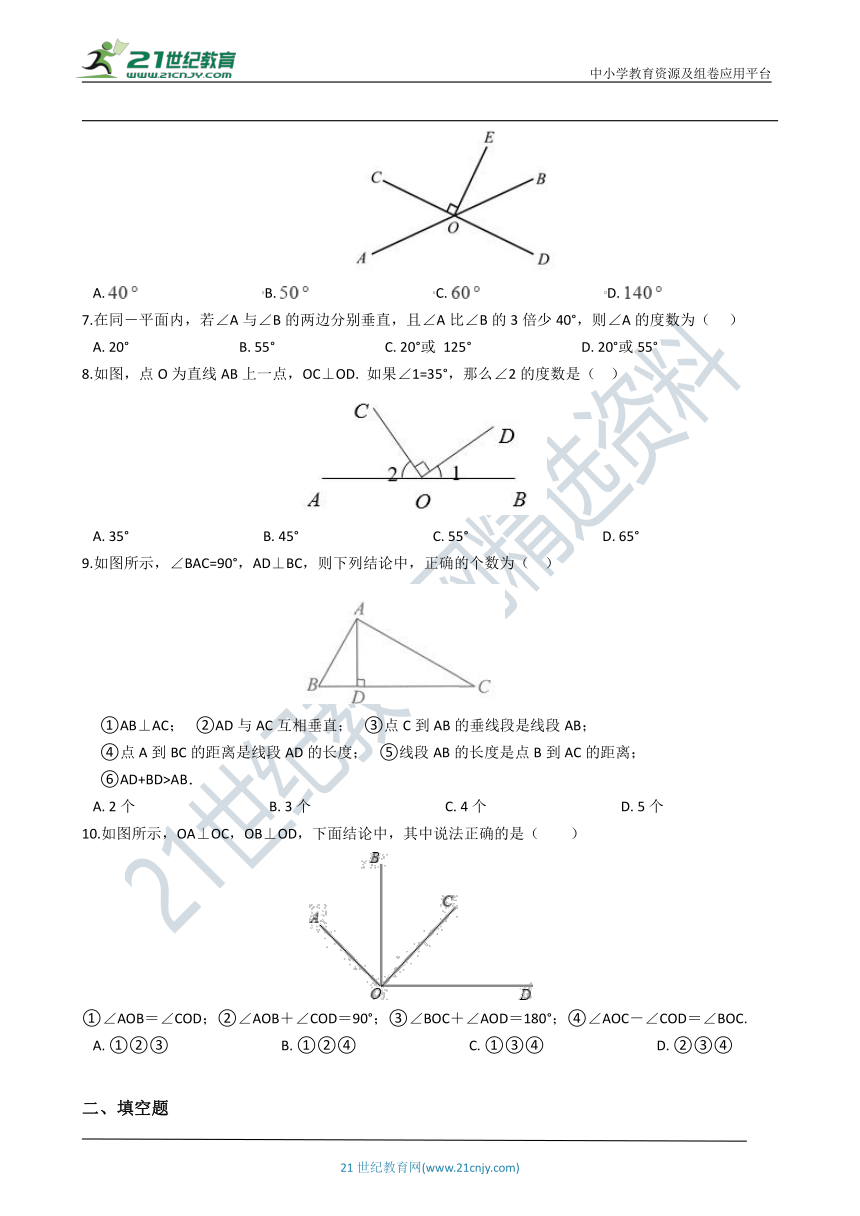
8.如图,点O为直线AB上一点,OC⊥OD. 如果∠1=35°,那么∠2的度数是(?? )
A.?35°???????????????????????????????????????B.?45°???????????????????????????????????????C.?55°???????????????????????????????????????D.?65°
9.如图所示,∠BAC=90°,AD⊥BC,则下列结论中,正确的个数为(?? )
??? ①AB⊥AC;? ②AD与AC互相垂直;? ③点C到AB的垂线段是线段AB;
??? ④点A到BC的距离是线段AD的长度;? ⑤线段AB的长度是点B到AC的距离;
??? ⑥AD+BD>AB.
A.?2个???????????????????????????????????????B.?3个???????????????????????????????????????C.?4个???????????????????????????????????????D.?5个
10.如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是( )
①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC.
A.?①②③????????????????????????????????B.?①②④????????????????????????????????C.?①③④????????????????????????????????D.?②③④
二、填空题
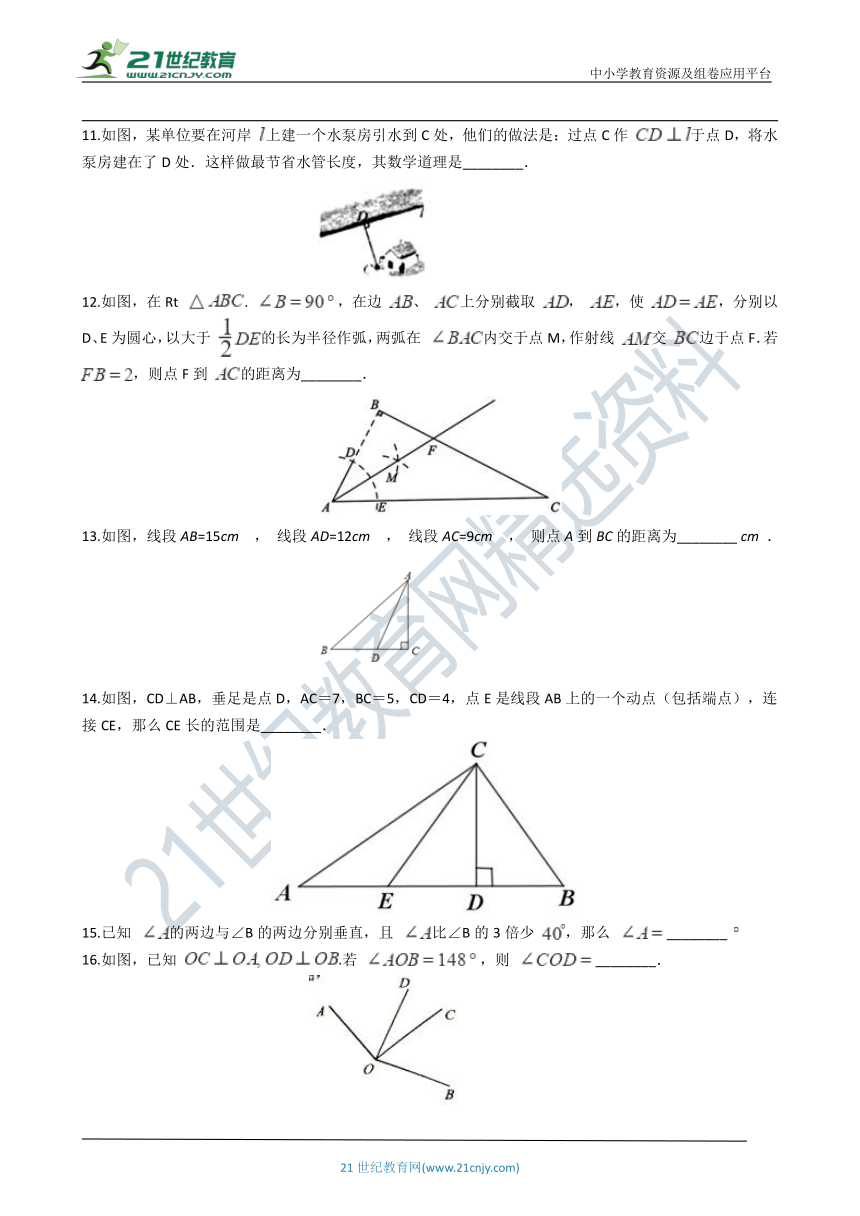
11.如图,某单位要在河岸 上建一个水泵房引水到C处,他们的做法是:过点C作 于点D,将水泵房建在了D处.这样做最节省水管长度,其数学道理是________.
12.如图,在Rt . ,在边 、 上分别截取 , ,使 ,分别以D、E为圆心,以大于 的长为半径作弧,两弧在 内交于点M,作射线 交 边于点F.若 ,则点F到 的距离为________.
?
13.如图,线段AB=15cm , 线段AD=12cm , 线段AC=9cm , 则点A到BC的距离为________ cm .
14.如图,CD⊥AB,垂足是点D,AC=7,BC=5,CD=4,点E是线段AB上的一个动点(包括端点),连接CE,那么CE长的范围是________.
15.已知 的两边与∠B的两边分别垂直,且 比∠B的3倍少 ,那么 ________
16.如图,已知 .若 ,则 ________.
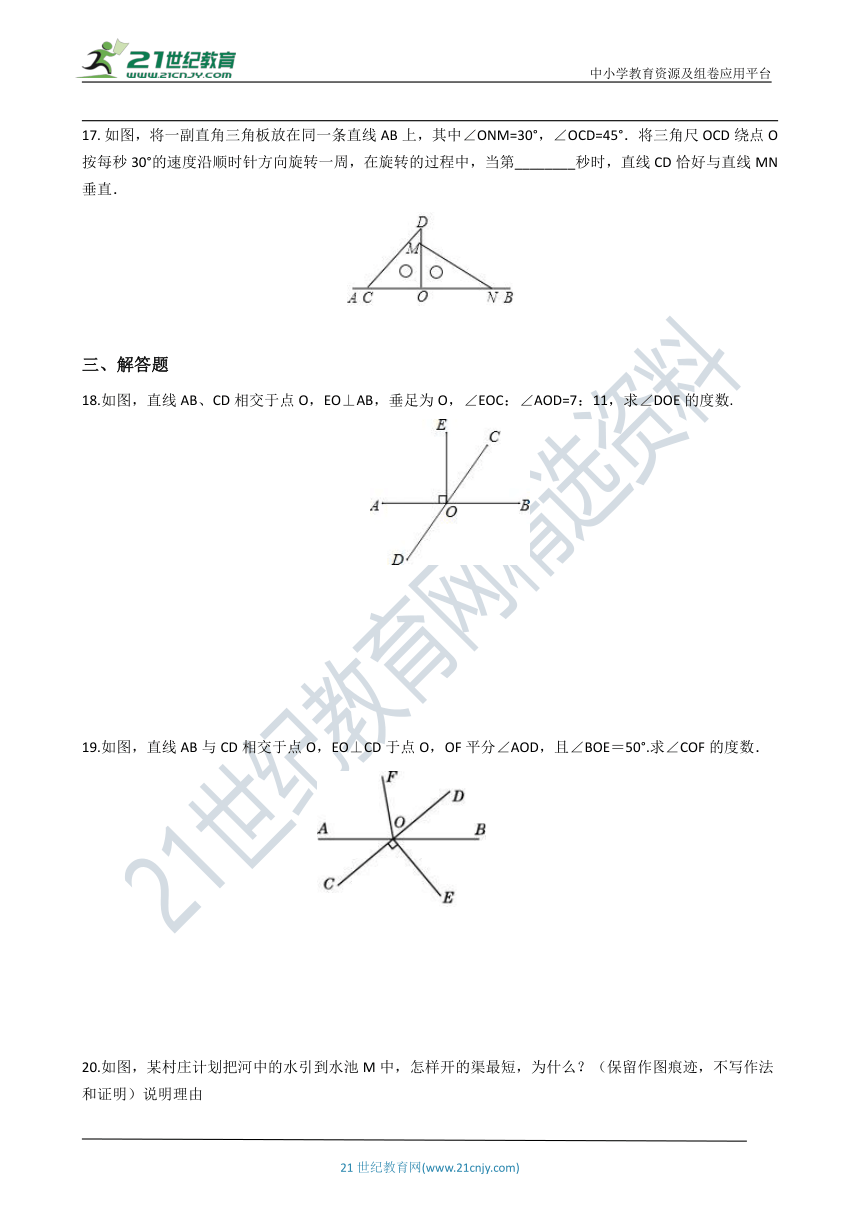
如图,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.将三角尺OCD绕点O按每秒30°的速度沿顺时针方向旋转一周,在旋转的过程中,当第________秒时,直线CD恰好与直线MN垂直.
三、解答题
18.如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC:∠AOD=7:11,求∠DOE的度数.?
19.如图,直线AB与CD相交于点O,EO⊥CD于点O,OF平分∠AOD,且∠BOE=50°.求∠COF的度数.
20.如图,某村庄计划把河中的水引到水池M中,怎样开的渠最短,为什么?(保留作图痕迹,不写作法和证明)说明理由
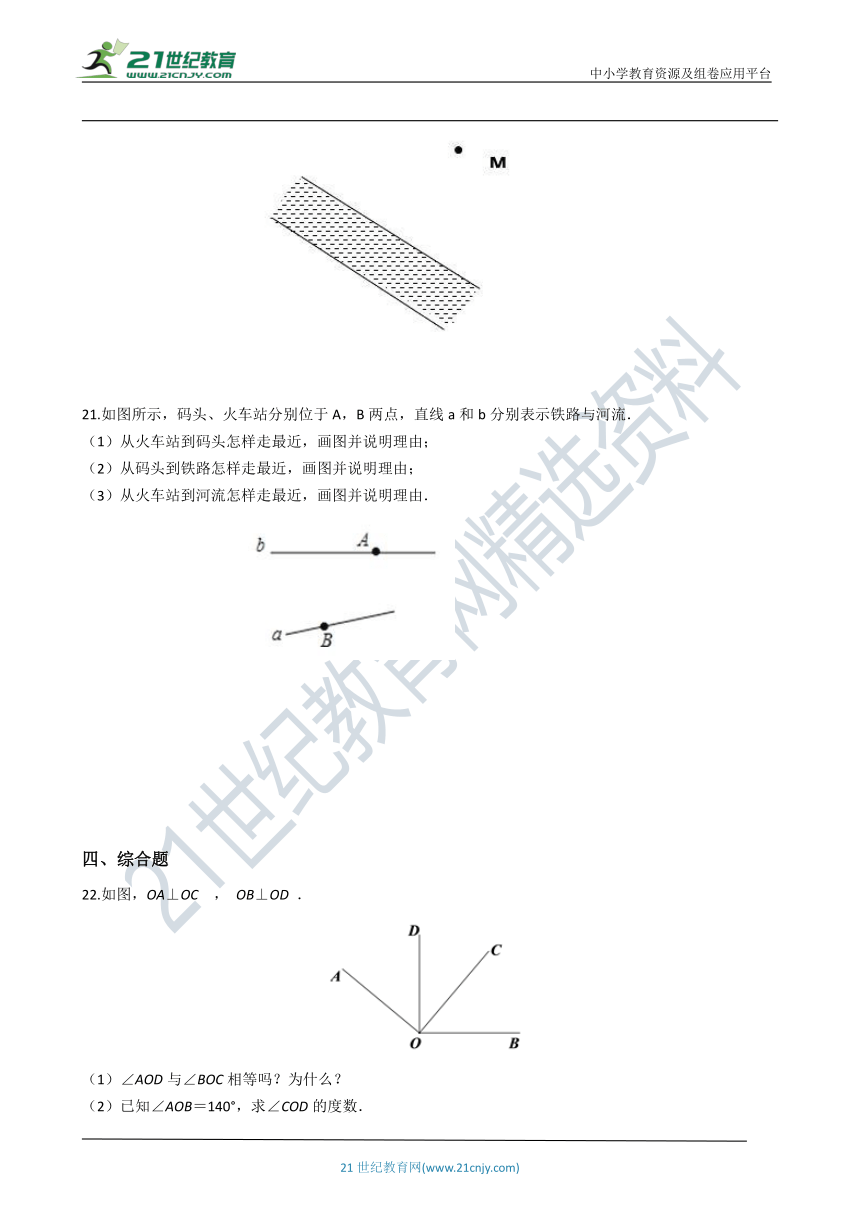
21.如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
四、综合题
22.如图,OA⊥OC , OB⊥OD .
(1)∠AOD与∠BOC相等吗?为什么?
(2)已知∠AOB=140°,求∠COD的度数.
答案解析部分
一、单选题
1.【答案】 D
【解析】解:由垂线段最短,可知 同一条边上的高线不可能比中线长,
只有当中线和高线重合时, ,
因此 ,
故答案为:D.
2.【答案】 A
【解析】解:∵PO⊥l,
∴这些线段PO,PA1 , PA2 , PA3 , …中,最短的线段是 PO.
故答案为:A.
3.【答案】 A
【解析】解:已知,在△ABC中,AC⊥BC,AC=4.5,
根据垂线段最短,可知AP的长不可小于4.5,当P和C重合时,AP=4.5,
故答案为:A.
4.【答案】 C
【解析】解:∵CP⊥AB,
∴把河中的水引到村庄C拟修水渠中最短的是CP.
故答案为:C.
5.【答案】 D
【解析】在同一平面内,画已知直线的垂线,可以画无数条;
故答案为:D.
6.【答案】 B
【解析】解:∵
∴
∵
∴
故答案为:B.
7.【答案】 C
【解析】解:设∠B是x度,根据题意,得
①两个角相等时,如图1:
∠B=∠A=x°,
x=3x-40
解得,x=20,
故∠A=20°,
②两个角互补时,如图2:
x+3x-40=180,
所以x=55,
3×55°-40°=125°
故∠A的度数为:20°或125°.
故答案为:C.
8.【答案】 C
【解析】解:∵OC⊥OD,
∴∠COD=90°
∵∠1+∠COD+∠2=180°
∴∠2=180°-90°-35°=55°.
故答案为:C.
9.【答案】C
【解析】∵∠BAC=90°,∴AB⊥AC,故①正确;
∵∠DAC<∠BAC=90°,∴AD与AC不垂直,故②错误;
点C到AB的垂线段是线段AC,故③错误;
点A到BC的距离是线段AD的长度,故④正确;
线段AB的长度是点B到AC的距离,故⑤正确;
在ABD中,根据两边之和大于第三边,AD+BD>AB,故⑥正确,
∴正确的为:①④⑤⑥.
故答案为:C.
10.【答案】C
【解析】由题意可知,OA⊥OC,所以∠AOC=90°,即∠AOB+∠BOC=90°.同时,OB⊥OD,所以∠BOD=90°,即∠COD+∠BOC=90°.依次,可以判定∠AOB=∠COD,所以①正确.又因为不能推断出∠AOB与∠COD的具体角度,所以②不正确.∠AOD=∠AOB+∠BOC+∠COD,所以∠BOC+∠AOD=∠BOC+∠AOB+∠BOC+∠COD=90°+90°=180°.因为∠AOB=∠COD,所以∠AOC-∠COD=∠AOC-∠AOB=∠BOC,所以④正确.为此,选C.
二、填空题
11.【答案】 垂线段最短
【解析】通过比较发现:直线外一点与直线上各点连结的所有线段中,垂线段最短.
故答案为:垂线段最短.
12.【答案】 2
【解析】解:根据作图过程可知:
AF平分∠BAC,
过点F作FG⊥AC,
∵∠B=90°,
∴FB⊥AB,
∴FG=FB=2.
∴点F到AC的距离为2.
故答案为:2.
13.【答案】 9
【解析】解:如图所示,已知 ,AC=9cm , 由点到直线的距离定义可知,点A到BC的距离为AC的长度,即为9cm;
故答案为:9.
14.【答案】 4≤CE≤7
【解析】解:∵CD⊥AB,垂足是点D,AC=7,BC=5,CD=4,
∴CE长的范围是4≤CE≤7,
故答案为:4≤CE≤7.
15.【答案】 20或125
【解析】解:设∠B是x度,根据题意,得
①两个角相等时,如图1:
∠B=∠A=x°,
x=3x-40,
解得,x=20,
故∠A=20°,
②两个角互补时,如图2:
x+3x-40=180,
所以x=55,
3×55°-40°=125°
综上所述:∠A的度数为:20°或125°.
故答案为:20或125.
16.【答案】
【解析】解:∵ .,
∴ ,
∵ ,
∴ ;
故答案为: .
17.【答案】5.5或11.5
【解析】解:如图,CD在OM的右边时,设CD与AB相交于G, ∵CD⊥MN,
∴∠NGC=90°﹣∠MNO=90°﹣30°=60°,
∴∠CON=∠NGC﹣∠OCD=60°﹣45°=15°,
∴旋转角为180°﹣∠CON=180°﹣15°=165°,
t=165°÷30°=5.5秒,
CD在OM的左边时,设CD与AB相交于G,
∵CD⊥MN,
∴∠NGD=90°﹣∠MNO=90°﹣30°=60°,
∴∠AOC=∠NGD﹣∠C=60°﹣45°=15°,
∴旋转角为360°﹣∠AOC=360°﹣15°=345°,
t=345°÷30°=11.5秒,
综上所述,第5.5或11.5秒时,直线CD恰好与直线MN垂直.
故答案为:5.5或11.5.
三、解答题
18.【答案】 解:∵EO⊥AB,?
∴∠EOA=90°,
∴∠EOC+∠AOD=90°,
∵∠EOC:∠AOD=7:11,
∴∠AOD=90°× =55°,
∴∠DOE=∠EOA+∠AOD=90°+55°=145°,
答:∠DOE的度数是145°.
【解析】由EO⊥AB可得∠AOE=90°,由此可得∠EOC+∠AOD=90°,结合∠EOC:∠AOD=7:11可求得∠AOD=55°,这样由∠DOE=∠EOA+∠AOD即可求得∠DOE的度数.
19.【答案】 解:∵EO⊥CD,
∴∠COE=90°,
又∵∠BOE=50°,
∴∠COB=∠COE+∠BOE=140°.
∵∠AOD=∠COB(对顶角相等),
∴∠AOD=140°,
∴∠COF= ∠AOD= 140°=75°.
【解析】先求∠COB的角度,再根据对顶角相等得出:∠AOD=∠COB,再根据角平分线的定义求得∠COF的度数.
20.【答案】解:理由是:垂线段最短 .
【解析】根据点到直线的所有连线中,垂线段最短分析作图即可.
21.【答案】 解:如图所示:
(1)沿AB走,两点之间线段最短;
(2)沿BD走,垂线段最短;
(3)沿AC走,垂线段最短.
【解析】(1)从火车站到码头的距离是点到点的距离,即两点间的距离.依据两点之间线段最短解答.
(2)从码头到铁路的距离是点到直线的距离.依据垂线段最短解答.
(3)从火车站到河流的距离是点到直线的距离.依据垂线段最短解答.
四、综合题
22.【答案】 (1)解:相等,理由如下:
∵AO⊥CO , DO⊥BO
∴∠AOC=∠BOD=90°
∴∠AOD+∠DOC=∠BOC+∠DOC
∴∠AOD=∠BOC
(2)解:∵∠AOB=140°,∠BOD=90°
∴∠AOD=∠AOB-∠BOD=50°
∵∠AOC=90°
∴∠COD=∠AOC-∠AOD=40°
答:∠COD的度数为40°
【解析】(1)利用垂直的定义,可知∠AOC=∠BOD,再利用同角的余角相等,可证得结论。
(2)此题解法不止一种,根据∠AOD=∠AOB-∠BOD,可求出∠AOD的度数,再利用∠COD=∠AOC-∠AOD,从而可求出∠COD的度数;或根据∠COD=∠AOC+∠BOD-∠AOB,即可求解。
一、单选题
1.若线段 , 分别是 边上的高线和中线,则(?? )
A.?????????????????????????B.?????????????????????????C.?????????????????????????D.?
2.如图,连接直线 外一点 与直线 上各点 , ,其中 ,这些线段 , , , , 中,最短的线段是(?? )
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
3.如图,AC⊥BC,AC=4.5,若点P在直线BC上,则AP的长可能是(??? ).
A.?5???????????????????????????????????????????B.?4???????????????????????????????????????????C.?3???????????????????????????????????????????D.?2
4.如图,把河 中的水引到村庄C拟修水渠中最短的是(? )
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
5.如图,在平面内作已知直线m的垂线,可作垂线的条数有(??? )
A.?0条?????????????????????????????????????B.?1条?????????????????????????????????????C.?2条?????????????????????????????????????D.?无数条
6.如图,直线 , 相交于点O, ,垂足为点O.若 ,则 的度数为(?? )
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
7.在同-平面内,若∠A与∠B的两边分别垂直,且∠A比∠B的3倍少40°,则∠A的度数为(??? )
A.?20°????????????????????????????????B.?55°????????????????????????????????C.?20°或 125°????????????????????????????????D.?20°或55°
8.如图,点O为直线AB上一点,OC⊥OD. 如果∠1=35°,那么∠2的度数是(?? )
A.?35°???????????????????????????????????????B.?45°???????????????????????????????????????C.?55°???????????????????????????????????????D.?65°
9.如图所示,∠BAC=90°,AD⊥BC,则下列结论中,正确的个数为(?? )
??? ①AB⊥AC;? ②AD与AC互相垂直;? ③点C到AB的垂线段是线段AB;
??? ④点A到BC的距离是线段AD的长度;? ⑤线段AB的长度是点B到AC的距离;
??? ⑥AD+BD>AB.
A.?2个???????????????????????????????????????B.?3个???????????????????????????????????????C.?4个???????????????????????????????????????D.?5个
10.如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是( )
①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC.
A.?①②③????????????????????????????????B.?①②④????????????????????????????????C.?①③④????????????????????????????????D.?②③④
二、填空题
11.如图,某单位要在河岸 上建一个水泵房引水到C处,他们的做法是:过点C作 于点D,将水泵房建在了D处.这样做最节省水管长度,其数学道理是________.
12.如图,在Rt . ,在边 、 上分别截取 , ,使 ,分别以D、E为圆心,以大于 的长为半径作弧,两弧在 内交于点M,作射线 交 边于点F.若 ,则点F到 的距离为________.
?
13.如图,线段AB=15cm , 线段AD=12cm , 线段AC=9cm , 则点A到BC的距离为________ cm .
14.如图,CD⊥AB,垂足是点D,AC=7,BC=5,CD=4,点E是线段AB上的一个动点(包括端点),连接CE,那么CE长的范围是________.
15.已知 的两边与∠B的两边分别垂直,且 比∠B的3倍少 ,那么 ________
16.如图,已知 .若 ,则 ________.
如图,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.将三角尺OCD绕点O按每秒30°的速度沿顺时针方向旋转一周,在旋转的过程中,当第________秒时,直线CD恰好与直线MN垂直.
三、解答题
18.如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC:∠AOD=7:11,求∠DOE的度数.?
19.如图,直线AB与CD相交于点O,EO⊥CD于点O,OF平分∠AOD,且∠BOE=50°.求∠COF的度数.
20.如图,某村庄计划把河中的水引到水池M中,怎样开的渠最短,为什么?(保留作图痕迹,不写作法和证明)说明理由
21.如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
四、综合题
22.如图,OA⊥OC , OB⊥OD .
(1)∠AOD与∠BOC相等吗?为什么?
(2)已知∠AOB=140°,求∠COD的度数.
答案解析部分
一、单选题
1.【答案】 D
【解析】解:由垂线段最短,可知 同一条边上的高线不可能比中线长,
只有当中线和高线重合时, ,
因此 ,
故答案为:D.
2.【答案】 A
【解析】解:∵PO⊥l,
∴这些线段PO,PA1 , PA2 , PA3 , …中,最短的线段是 PO.
故答案为:A.
3.【答案】 A
【解析】解:已知,在△ABC中,AC⊥BC,AC=4.5,
根据垂线段最短,可知AP的长不可小于4.5,当P和C重合时,AP=4.5,
故答案为:A.
4.【答案】 C
【解析】解:∵CP⊥AB,
∴把河中的水引到村庄C拟修水渠中最短的是CP.
故答案为:C.
5.【答案】 D
【解析】在同一平面内,画已知直线的垂线,可以画无数条;
故答案为:D.
6.【答案】 B
【解析】解:∵
∴
∵
∴
故答案为:B.
7.【答案】 C
【解析】解:设∠B是x度,根据题意,得
①两个角相等时,如图1:
∠B=∠A=x°,
x=3x-40
解得,x=20,
故∠A=20°,
②两个角互补时,如图2:
x+3x-40=180,
所以x=55,
3×55°-40°=125°
故∠A的度数为:20°或125°.
故答案为:C.
8.【答案】 C
【解析】解:∵OC⊥OD,
∴∠COD=90°
∵∠1+∠COD+∠2=180°
∴∠2=180°-90°-35°=55°.
故答案为:C.
9.【答案】C
【解析】∵∠BAC=90°,∴AB⊥AC,故①正确;
∵∠DAC<∠BAC=90°,∴AD与AC不垂直,故②错误;
点C到AB的垂线段是线段AC,故③错误;
点A到BC的距离是线段AD的长度,故④正确;
线段AB的长度是点B到AC的距离,故⑤正确;
在ABD中,根据两边之和大于第三边,AD+BD>AB,故⑥正确,
∴正确的为:①④⑤⑥.
故答案为:C.
10.【答案】C
【解析】由题意可知,OA⊥OC,所以∠AOC=90°,即∠AOB+∠BOC=90°.同时,OB⊥OD,所以∠BOD=90°,即∠COD+∠BOC=90°.依次,可以判定∠AOB=∠COD,所以①正确.又因为不能推断出∠AOB与∠COD的具体角度,所以②不正确.∠AOD=∠AOB+∠BOC+∠COD,所以∠BOC+∠AOD=∠BOC+∠AOB+∠BOC+∠COD=90°+90°=180°.因为∠AOB=∠COD,所以∠AOC-∠COD=∠AOC-∠AOB=∠BOC,所以④正确.为此,选C.
二、填空题
11.【答案】 垂线段最短
【解析】通过比较发现:直线外一点与直线上各点连结的所有线段中,垂线段最短.
故答案为:垂线段最短.
12.【答案】 2
【解析】解:根据作图过程可知:
AF平分∠BAC,
过点F作FG⊥AC,
∵∠B=90°,
∴FB⊥AB,
∴FG=FB=2.
∴点F到AC的距离为2.
故答案为:2.
13.【答案】 9
【解析】解:如图所示,已知 ,AC=9cm , 由点到直线的距离定义可知,点A到BC的距离为AC的长度,即为9cm;
故答案为:9.
14.【答案】 4≤CE≤7
【解析】解:∵CD⊥AB,垂足是点D,AC=7,BC=5,CD=4,
∴CE长的范围是4≤CE≤7,
故答案为:4≤CE≤7.
15.【答案】 20或125
【解析】解:设∠B是x度,根据题意,得
①两个角相等时,如图1:
∠B=∠A=x°,
x=3x-40,
解得,x=20,
故∠A=20°,
②两个角互补时,如图2:
x+3x-40=180,
所以x=55,
3×55°-40°=125°
综上所述:∠A的度数为:20°或125°.
故答案为:20或125.
16.【答案】
【解析】解:∵ .,
∴ ,
∵ ,
∴ ;
故答案为: .
17.【答案】5.5或11.5
【解析】解:如图,CD在OM的右边时,设CD与AB相交于G, ∵CD⊥MN,
∴∠NGC=90°﹣∠MNO=90°﹣30°=60°,
∴∠CON=∠NGC﹣∠OCD=60°﹣45°=15°,
∴旋转角为180°﹣∠CON=180°﹣15°=165°,
t=165°÷30°=5.5秒,
CD在OM的左边时,设CD与AB相交于G,
∵CD⊥MN,
∴∠NGD=90°﹣∠MNO=90°﹣30°=60°,
∴∠AOC=∠NGD﹣∠C=60°﹣45°=15°,
∴旋转角为360°﹣∠AOC=360°﹣15°=345°,
t=345°÷30°=11.5秒,
综上所述,第5.5或11.5秒时,直线CD恰好与直线MN垂直.
故答案为:5.5或11.5.
三、解答题
18.【答案】 解:∵EO⊥AB,?
∴∠EOA=90°,
∴∠EOC+∠AOD=90°,
∵∠EOC:∠AOD=7:11,
∴∠AOD=90°× =55°,
∴∠DOE=∠EOA+∠AOD=90°+55°=145°,
答:∠DOE的度数是145°.
【解析】由EO⊥AB可得∠AOE=90°,由此可得∠EOC+∠AOD=90°,结合∠EOC:∠AOD=7:11可求得∠AOD=55°,这样由∠DOE=∠EOA+∠AOD即可求得∠DOE的度数.
19.【答案】 解:∵EO⊥CD,
∴∠COE=90°,
又∵∠BOE=50°,
∴∠COB=∠COE+∠BOE=140°.
∵∠AOD=∠COB(对顶角相等),
∴∠AOD=140°,
∴∠COF= ∠AOD= 140°=75°.
【解析】先求∠COB的角度,再根据对顶角相等得出:∠AOD=∠COB,再根据角平分线的定义求得∠COF的度数.
20.【答案】解:理由是:垂线段最短 .
【解析】根据点到直线的所有连线中,垂线段最短分析作图即可.
21.【答案】 解:如图所示:
(1)沿AB走,两点之间线段最短;
(2)沿BD走,垂线段最短;
(3)沿AC走,垂线段最短.
【解析】(1)从火车站到码头的距离是点到点的距离,即两点间的距离.依据两点之间线段最短解答.
(2)从码头到铁路的距离是点到直线的距离.依据垂线段最短解答.
(3)从火车站到河流的距离是点到直线的距离.依据垂线段最短解答.
四、综合题
22.【答案】 (1)解:相等,理由如下:
∵AO⊥CO , DO⊥BO
∴∠AOC=∠BOD=90°
∴∠AOD+∠DOC=∠BOC+∠DOC
∴∠AOD=∠BOC
(2)解:∵∠AOB=140°,∠BOD=90°
∴∠AOD=∠AOB-∠BOD=50°
∵∠AOC=90°
∴∠COD=∠AOC-∠AOD=40°
答:∠COD的度数为40°
【解析】(1)利用垂直的定义,可知∠AOC=∠BOD,再利用同角的余角相等,可证得结论。
(2)此题解法不止一种,根据∠AOD=∠AOB-∠BOD,可求出∠AOD的度数,再利用∠COD=∠AOC-∠AOD,从而可求出∠COD的度数;或根据∠COD=∠AOC+∠BOD-∠AOB,即可求解。
