5.1.3 同位角、内错角、同旁内角同步练习(含解析)
文档属性
| 名称 | 5.1.3 同位角、内错角、同旁内角同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 09:46:49 | ||
图片预览




文档简介
人教版数学七年级下册 第五章 相交线与平行线 5.1.3 同位角、内错角、同旁内角 同步练习
一、单选题
1.如图,直线a,b被直线c所截,则∠1与∠2的位置关系是(?? )
A.?同位角???????????????????????????????B.?内错角???????????????????????????????C.?同旁内角???????????????????????????????D.?邻补角
2.如图,下列选项中与∠A是同旁内角的是(? ?)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
3.如图,下列四个角中,与∠1构成一对同位角的是(?? )
A.?∠2????????????????????????????????????????B.?∠3????????????????????????????????????????C.?∠4????????????????????????????????????????D.?∠5
4.如图所示,下列说法不正确的是(? )
A.?∠1和∠4是内错角??????????B.?∠1和∠3是对顶角??????????C.?∠3和∠4是同位角??????????D.?∠2和∠4是同旁内角
5.如图所示,下列说法错误的是(??? )
A.?与 是对顶角?????????????????????????????????????????B.?与 是同旁内角
C.?与 是内错角?????????????????????????????????????????D.?与 是同位角
6.已知∠1和∠2是同旁内角.若∠1=40°,则∠2的度数是( ??)
A.?40°???????????????????????????????????B.?140°???????????????????????????????????C.?160°???????????????????????????????????D.?无法确定
7.若∠a与∠β是内错角,且∠a=50°时,则∠β的度数为(??? )
A.?50°????????????????????????????????B.?130°????????????????????????????????C.?50°或130°????????????????????????????????D.?无法确定
8.如图所示,与∠α构成同位角的角的个数为( )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
9.如图,下列6种说法:①∠1与∠4是内错角;②∠1与∠2是同位角;③∠2与∠4是内错角;④∠4与∠5是同旁内角;⑤∠2与∠4是同位角;⑥∠2与∠5是内错角.其中正确的有 ( ????)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题
10.如图,有下列3个结论:①能与∠DEF构成内错角的角的个数是2;②能与∠EFB构成同位角的角的个数是1;③能与∠C构成同旁内角的角的个数是4,以上结论正确的是________.
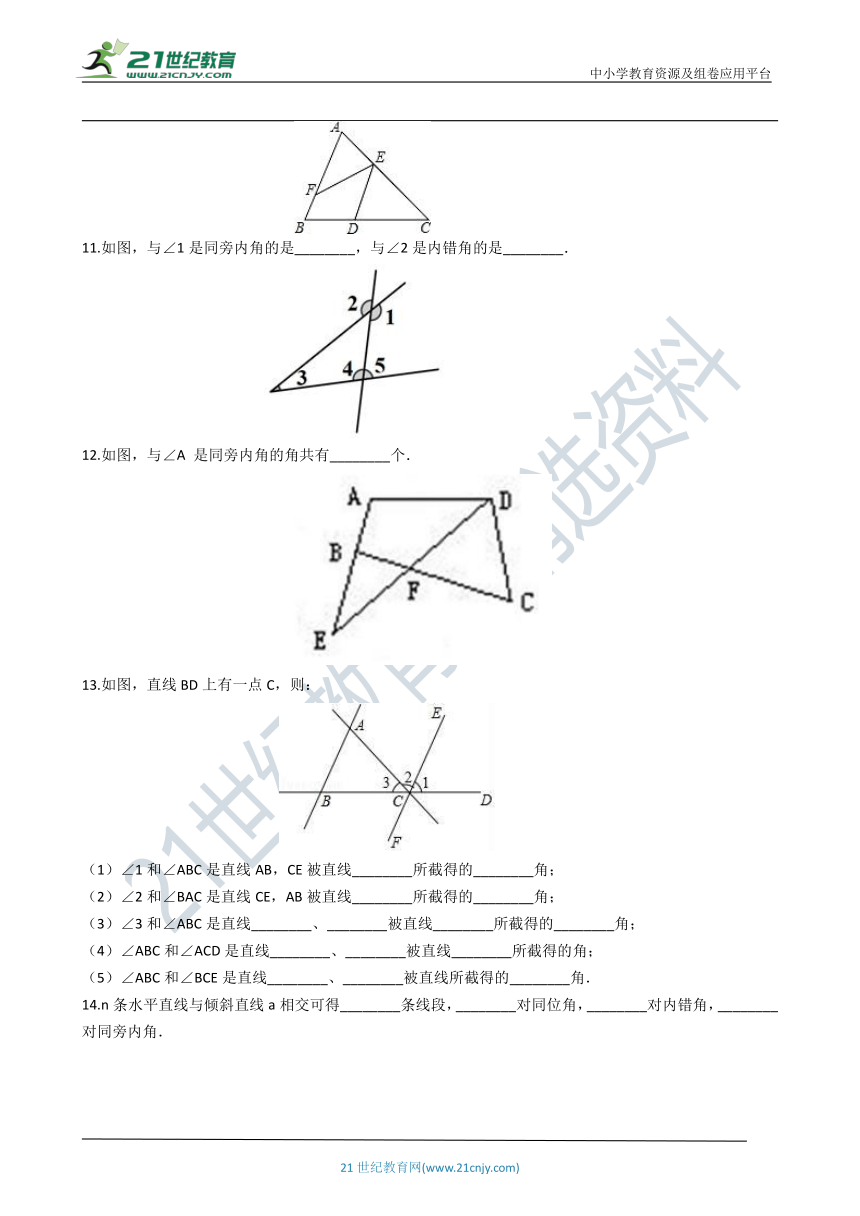
11.如图,与∠1是同旁内角的是________,与∠2是内错角的是________.
12.如图,与∠A 是同旁内角的角共有________个.
13.如图,直线BD上有一点C,则:
(1)∠1和∠ABC是直线AB,CE被直线________所截得的________角;
(2)∠2和∠BAC是直线CE,AB被直线________所截得的________角;
(3)∠3和∠ABC是直线________、________被直线________所截得的________角;
(4)∠ABC和∠ACD是直线________、________被直线________所截得的角;
(5)∠ABC和∠BCE是直线________、________被直线所截得的________角.
14.n条水平直线与倾斜直线a相交可得________条线段,________对同位角,________对内错角,________对同旁内角.
三、解答题
15.如图,已知直线a,b被直线c,d所截,直线a,c,d相交于点O,按要求完成下列各小题.
(1)在图中的∠1~∠9这9个角中,同位角共有多少对?请你全部写出来;
(2)∠4和∠5是什么位置关系的角?∠6和∠8之间的位置关系与∠4和∠5的相同吗?
16.两条直线被第三条直线所截,∠1是∠2的同旁内角,∠3是∠2的内错角.若∠1=3∠2,∠2=3∠3,求∠1、∠2的度数.
17.如图,
(1)指出直线AB,CD被AC所截形成的内错角;
(2)指出直线AB,CD被BE所截形成的同位角;
(3)找出图中∠1的所有同旁内角
18.如图,BCD是一条直线,∠1=∠B,∠2=∠A,指出∠1的同位角,∠2的内错角,并求出∠A+∠B+∠ACB的度数.
四、综合题
19.两条直线被第三条直线所截,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图,标出∠1,∠2,∠3.
(2)若∠1=2∠2,∠2=2∠3,求∠3的度数.
答案解析部分
一、单选题
1.【答案】 A
【解析】解:如图所示,∠1和∠2两个角都在两被截直线直线b和a同侧,并且在第三条直线c(截线)的同旁,故∠1和∠2是直线b、a被c所截而成的同位角.
故答案为:A.
2.【答案】 A
【解析】解:A、∠1和∠A是同旁内角,故本选项符合题意;
B、∠2和∠A是同位角,不是同旁内角,故本选项不符合题意;
C、∠3和∠A不是同旁内角,故本选项不符合题意;
D、∠4和∠A是内错角,不是同旁内角,故本选项不符合题意.
故答案为:A.
3.【答案】 B
【解析】解:由图可得,与∠1构成同位角的是∠3,
故答案为:B.
4.【答案】 D
【解析】解:由图可得,∠1和∠4是内错角,∠1和∠3是对顶角,∠3和∠4是同位角,∠2和∠4是同位角,而不是同旁内角,
故答案为:D.
5.【答案】 B
【解析】解:A. 与 是对顶角,故A选项不符合题意;
B. 与 不是同旁内角,故B符合题意;
C. 与 是内错角,故C选项不符合题意;
D. 与 是同位角,故D不选项符合题意.
故答案为:B.
6.【答案】 D
【解析】解:∵ ∠1和∠2是同旁内角,
∴∠1+∠2不一定互补,
∴∠2的度数无法确定。
故答案为:D
7.【答案】 D
【解析】解:∵两个角为内错角
∴没有规定的直线平行的情况下,内错角的度数无法确定。
故答案为:D。
8.【答案】 C
【解析】根据同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.同时,同位角的边构成“F“形,由此可判断,与∠α构成同位角的角为∠ACD,∠FAC,∠FAE.
9.【答案】 C
【解析】根据同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角作答.所以,题干中只有②④⑥正确,所以选C.
二、填空题
10.【答案】 ①②
【解析】解:①能与 构成内错角的角的个数有2个,即 和 ,故正确;
②能与 构成同位角的角的个数只有1个:即 ,故正确;
③能与 构成同旁内角的角的个数有5个:即 , , , , ,故错误;
所以结论正确的是①②.
故答案为:①②.
11.【答案】 ∠5;∠3
【解析】解:如图,与∠1是同旁内角的是∠5,与∠2是内错角的是∠3.
故答案为:∠5;∠3.
12.【答案】 4
【解析】根据同旁内角的定义可得∠A的同旁内角有:∠ABC,∠ADC,∠ADE,∠E,共4个.
故答案为:4.
13.【答案】 (1)BD(或BC);同位
(2)AC;内错
(3)AB;AC;BC;同旁内
(4)AB;AC;BC
(5)AB;CE;同旁内
【解析】(1)∠1和∠ABC是直线AB,CE被直线BD(或BC)所截得的同位角;(2)∠2和∠BAC是直线CE,AB被直线AC所截得的内错角;(3)∠3和∠ABC是直线AB,AC被直线BC所截得的同旁内角;(4)∠ABC和∠ACD是直线AB,AC被直线BC所截得的同位角;(5)∠ABC和∠BCE是直线AB,CE被直线所截得的同旁内角.
14.【答案】 ;2n(n﹣1);n(n﹣1);n(n﹣1)
【解析】解:n条水平直线与倾斜直线a相交可得 条线段,2n(n﹣1)对同位角,n(n﹣1)对内错角,n(n﹣1)对同旁内角。
三、解答题
15.【答案】 解:(1)如图所示:同位角共有5对:
分别是∠1和∠5,∠2和∠3,∠3和∠7,∠4和∠6,∠4和∠9;
(2)∠4和∠5是同旁内角,∠6和∠8也是同旁内角,故∠6和∠8之间的位置关系与∠4和∠5的相同.
【解析】(1)直接利用两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角,进而得出答案;
(2)直接利用两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角,进而得出答案.
16.【答案】 解:由∠1=3∠2,∠2=3∠3,得
∠1=9∠3.
由∠1是∠2的同旁内角,∠3是∠2的内错角,得
∠1与∠3是邻补角.
由邻补角角的性质,得
∠1+∠3=180°.
等量代换,得9∠3+∠3=180°,
解得∠3=18°.
∠1=9∠3=9×18°=162°,
∠2=3∠3=3×18°=54°.
【解析】根据等量代换,可得∠1与∠3的关系,再根据邻补角的性质,可得∠3的值,根据∠1、∠2、∠3的关系,可得答案.
17.【答案】 解:(1)直线AB,CD被AC所截形成的内错角是∠3和∠4;
(2)直线AB,CD被BE所截形成的同位角是∠B和∠DCE;
(3)∠1的所有同旁内角:∠4,∠D,∠ACE.
【解析】(1)根据内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角进行分析可得答案;
(2)根据同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角分析可得答案;
(3)根据同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角分析可得答案.
18.【答案】 ∠1的同位角是∠B,∠2的内错角∠A,180°
【解析】根据同位角就是:两个角都在截线的同旁,又分别处在被截的两条直线同侧的位置的角.内错角就是:两个角都在截线的两侧,又分别处在被截的两条直线中间位置的角;根据等量代换,角的和差,可得答案.由同位角的定义,内错角的定义,得∠1的同位角是∠B,∠2的内错角∠A,
由角的和差,得∠A+∠B+∠ACB=∠ACB+∠1+∠2=180°.
本题考查了同位角、内错角、同旁内角,解答此类题确定三线八角是关键,可直接从截线入手.对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义.
四、综合题
19.【答案】 (1)解:如图所示:
(2)解:∵∠1=2∠2,∠2=2∠3,
∴设∠3=x,则∠2=2x,∠1=4x,
故x+4x=180°,
解得:x=36°,
故∠3的度数为36°.
【解析】根据题意先画出图形, 设∠3=x,可得∠2=2x,∠1=4x,根据∠1与∠3是邻补角列出方程,求出x值即可.
一、单选题
1.如图,直线a,b被直线c所截,则∠1与∠2的位置关系是(?? )
A.?同位角???????????????????????????????B.?内错角???????????????????????????????C.?同旁内角???????????????????????????????D.?邻补角
2.如图,下列选项中与∠A是同旁内角的是(? ?)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
3.如图,下列四个角中,与∠1构成一对同位角的是(?? )
A.?∠2????????????????????????????????????????B.?∠3????????????????????????????????????????C.?∠4????????????????????????????????????????D.?∠5
4.如图所示,下列说法不正确的是(? )
A.?∠1和∠4是内错角??????????B.?∠1和∠3是对顶角??????????C.?∠3和∠4是同位角??????????D.?∠2和∠4是同旁内角
5.如图所示,下列说法错误的是(??? )
A.?与 是对顶角?????????????????????????????????????????B.?与 是同旁内角
C.?与 是内错角?????????????????????????????????????????D.?与 是同位角
6.已知∠1和∠2是同旁内角.若∠1=40°,则∠2的度数是( ??)
A.?40°???????????????????????????????????B.?140°???????????????????????????????????C.?160°???????????????????????????????????D.?无法确定
7.若∠a与∠β是内错角,且∠a=50°时,则∠β的度数为(??? )
A.?50°????????????????????????????????B.?130°????????????????????????????????C.?50°或130°????????????????????????????????D.?无法确定
8.如图所示,与∠α构成同位角的角的个数为( )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
9.如图,下列6种说法:①∠1与∠4是内错角;②∠1与∠2是同位角;③∠2与∠4是内错角;④∠4与∠5是同旁内角;⑤∠2与∠4是同位角;⑥∠2与∠5是内错角.其中正确的有 ( ????)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题
10.如图,有下列3个结论:①能与∠DEF构成内错角的角的个数是2;②能与∠EFB构成同位角的角的个数是1;③能与∠C构成同旁内角的角的个数是4,以上结论正确的是________.
11.如图,与∠1是同旁内角的是________,与∠2是内错角的是________.
12.如图,与∠A 是同旁内角的角共有________个.
13.如图,直线BD上有一点C,则:
(1)∠1和∠ABC是直线AB,CE被直线________所截得的________角;
(2)∠2和∠BAC是直线CE,AB被直线________所截得的________角;
(3)∠3和∠ABC是直线________、________被直线________所截得的________角;
(4)∠ABC和∠ACD是直线________、________被直线________所截得的角;
(5)∠ABC和∠BCE是直线________、________被直线所截得的________角.
14.n条水平直线与倾斜直线a相交可得________条线段,________对同位角,________对内错角,________对同旁内角.
三、解答题
15.如图,已知直线a,b被直线c,d所截,直线a,c,d相交于点O,按要求完成下列各小题.
(1)在图中的∠1~∠9这9个角中,同位角共有多少对?请你全部写出来;
(2)∠4和∠5是什么位置关系的角?∠6和∠8之间的位置关系与∠4和∠5的相同吗?
16.两条直线被第三条直线所截,∠1是∠2的同旁内角,∠3是∠2的内错角.若∠1=3∠2,∠2=3∠3,求∠1、∠2的度数.
17.如图,
(1)指出直线AB,CD被AC所截形成的内错角;
(2)指出直线AB,CD被BE所截形成的同位角;
(3)找出图中∠1的所有同旁内角
18.如图,BCD是一条直线,∠1=∠B,∠2=∠A,指出∠1的同位角,∠2的内错角,并求出∠A+∠B+∠ACB的度数.
四、综合题
19.两条直线被第三条直线所截,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图,标出∠1,∠2,∠3.
(2)若∠1=2∠2,∠2=2∠3,求∠3的度数.
答案解析部分
一、单选题
1.【答案】 A
【解析】解:如图所示,∠1和∠2两个角都在两被截直线直线b和a同侧,并且在第三条直线c(截线)的同旁,故∠1和∠2是直线b、a被c所截而成的同位角.
故答案为:A.
2.【答案】 A
【解析】解:A、∠1和∠A是同旁内角,故本选项符合题意;
B、∠2和∠A是同位角,不是同旁内角,故本选项不符合题意;
C、∠3和∠A不是同旁内角,故本选项不符合题意;
D、∠4和∠A是内错角,不是同旁内角,故本选项不符合题意.
故答案为:A.
3.【答案】 B
【解析】解:由图可得,与∠1构成同位角的是∠3,
故答案为:B.
4.【答案】 D
【解析】解:由图可得,∠1和∠4是内错角,∠1和∠3是对顶角,∠3和∠4是同位角,∠2和∠4是同位角,而不是同旁内角,
故答案为:D.
5.【答案】 B
【解析】解:A. 与 是对顶角,故A选项不符合题意;
B. 与 不是同旁内角,故B符合题意;
C. 与 是内错角,故C选项不符合题意;
D. 与 是同位角,故D不选项符合题意.
故答案为:B.
6.【答案】 D
【解析】解:∵ ∠1和∠2是同旁内角,
∴∠1+∠2不一定互补,
∴∠2的度数无法确定。
故答案为:D
7.【答案】 D
【解析】解:∵两个角为内错角
∴没有规定的直线平行的情况下,内错角的度数无法确定。
故答案为:D。
8.【答案】 C
【解析】根据同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.同时,同位角的边构成“F“形,由此可判断,与∠α构成同位角的角为∠ACD,∠FAC,∠FAE.
9.【答案】 C
【解析】根据同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角作答.所以,题干中只有②④⑥正确,所以选C.
二、填空题
10.【答案】 ①②
【解析】解:①能与 构成内错角的角的个数有2个,即 和 ,故正确;
②能与 构成同位角的角的个数只有1个:即 ,故正确;
③能与 构成同旁内角的角的个数有5个:即 , , , , ,故错误;
所以结论正确的是①②.
故答案为:①②.
11.【答案】 ∠5;∠3
【解析】解:如图,与∠1是同旁内角的是∠5,与∠2是内错角的是∠3.
故答案为:∠5;∠3.
12.【答案】 4
【解析】根据同旁内角的定义可得∠A的同旁内角有:∠ABC,∠ADC,∠ADE,∠E,共4个.
故答案为:4.
13.【答案】 (1)BD(或BC);同位
(2)AC;内错
(3)AB;AC;BC;同旁内
(4)AB;AC;BC
(5)AB;CE;同旁内
【解析】(1)∠1和∠ABC是直线AB,CE被直线BD(或BC)所截得的同位角;(2)∠2和∠BAC是直线CE,AB被直线AC所截得的内错角;(3)∠3和∠ABC是直线AB,AC被直线BC所截得的同旁内角;(4)∠ABC和∠ACD是直线AB,AC被直线BC所截得的同位角;(5)∠ABC和∠BCE是直线AB,CE被直线所截得的同旁内角.
14.【答案】 ;2n(n﹣1);n(n﹣1);n(n﹣1)
【解析】解:n条水平直线与倾斜直线a相交可得 条线段,2n(n﹣1)对同位角,n(n﹣1)对内错角,n(n﹣1)对同旁内角。
三、解答题
15.【答案】 解:(1)如图所示:同位角共有5对:
分别是∠1和∠5,∠2和∠3,∠3和∠7,∠4和∠6,∠4和∠9;
(2)∠4和∠5是同旁内角,∠6和∠8也是同旁内角,故∠6和∠8之间的位置关系与∠4和∠5的相同.
【解析】(1)直接利用两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角,进而得出答案;
(2)直接利用两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角,进而得出答案.
16.【答案】 解:由∠1=3∠2,∠2=3∠3,得
∠1=9∠3.
由∠1是∠2的同旁内角,∠3是∠2的内错角,得
∠1与∠3是邻补角.
由邻补角角的性质,得
∠1+∠3=180°.
等量代换,得9∠3+∠3=180°,
解得∠3=18°.
∠1=9∠3=9×18°=162°,
∠2=3∠3=3×18°=54°.
【解析】根据等量代换,可得∠1与∠3的关系,再根据邻补角的性质,可得∠3的值,根据∠1、∠2、∠3的关系,可得答案.
17.【答案】 解:(1)直线AB,CD被AC所截形成的内错角是∠3和∠4;
(2)直线AB,CD被BE所截形成的同位角是∠B和∠DCE;
(3)∠1的所有同旁内角:∠4,∠D,∠ACE.
【解析】(1)根据内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角进行分析可得答案;
(2)根据同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角分析可得答案;
(3)根据同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角分析可得答案.
18.【答案】 ∠1的同位角是∠B,∠2的内错角∠A,180°
【解析】根据同位角就是:两个角都在截线的同旁,又分别处在被截的两条直线同侧的位置的角.内错角就是:两个角都在截线的两侧,又分别处在被截的两条直线中间位置的角;根据等量代换,角的和差,可得答案.由同位角的定义,内错角的定义,得∠1的同位角是∠B,∠2的内错角∠A,
由角的和差,得∠A+∠B+∠ACB=∠ACB+∠1+∠2=180°.
本题考查了同位角、内错角、同旁内角,解答此类题确定三线八角是关键,可直接从截线入手.对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义.
四、综合题
19.【答案】 (1)解:如图所示:
(2)解:∵∠1=2∠2,∠2=2∠3,
∴设∠3=x,则∠2=2x,∠1=4x,
故x+4x=180°,
解得:x=36°,
故∠3的度数为36°.
【解析】根据题意先画出图形, 设∠3=x,可得∠2=2x,∠1=4x,根据∠1与∠3是邻补角列出方程,求出x值即可.
