5.1.1 相交线同步练习(含解析)
图片预览
文档简介
人教版数学七年级下册 第五章 相交线与平行线 5.1.1 相交线 同步练习
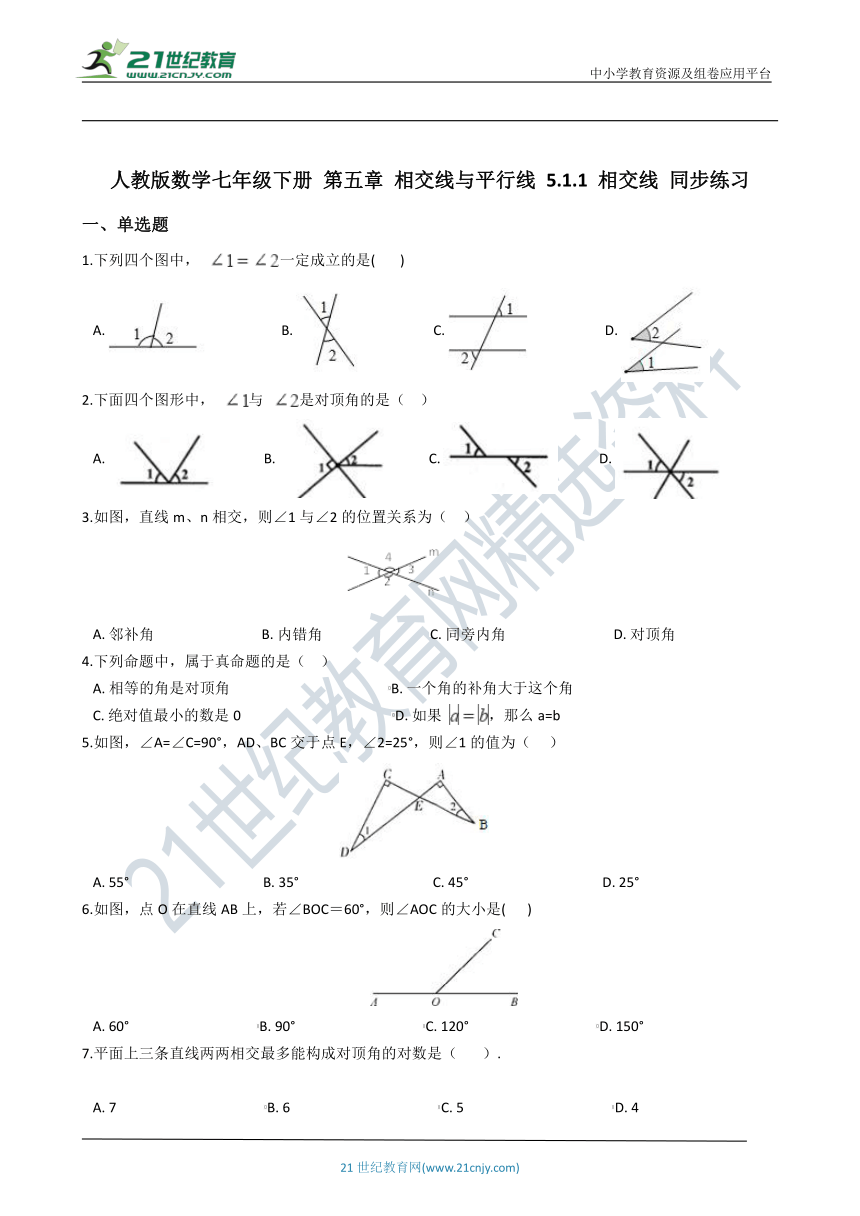
一、单选题
1.下列四个图中, 一定成立的是(????? )
A.????????????????????B.????????????????????C.????????????????????D.?
2.下面四个图形中, 与 是对顶角的是(?? )
A.?????????????B.?????????????C.?????????????D.?
3.如图,直线m、n相交,则∠1与∠2的位置关系为( )
A.?邻补角???????????????????????????????B.?内错角???????????????????????????????C.?同旁内角???????????????????????????????D.?对顶角
4.下列命题中,属于真命题的是(?? )
A.?相等的角是对顶角??????????????????????????????????????????????B.?一个角的补角大于这个角
C.?绝对值最小的数是0????????????????????????????????????????????D.?如果 ,那么a=b
5.如图,∠A=∠C=90°,AD、BC交于点E,∠2=25°,则∠1的值为( ???)
A.?55°???????????????????????????????????????B.?35°???????????????????????????????????????C.?45°???????????????????????????????????????D.?25°
6.如图,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是(???? )
A.?60°?????????????????????????????????????B.?90°?????????????????????????????????????C.?120°?????????????????????????????????????D.?150°
7.平面上三条直线两两相交最多能构成对顶角的对数是(????? ).
A.?7???????????????????????????????????????????B.?6???????????????????????????????????????????C.?5???????????????????????????????????????????D.?4
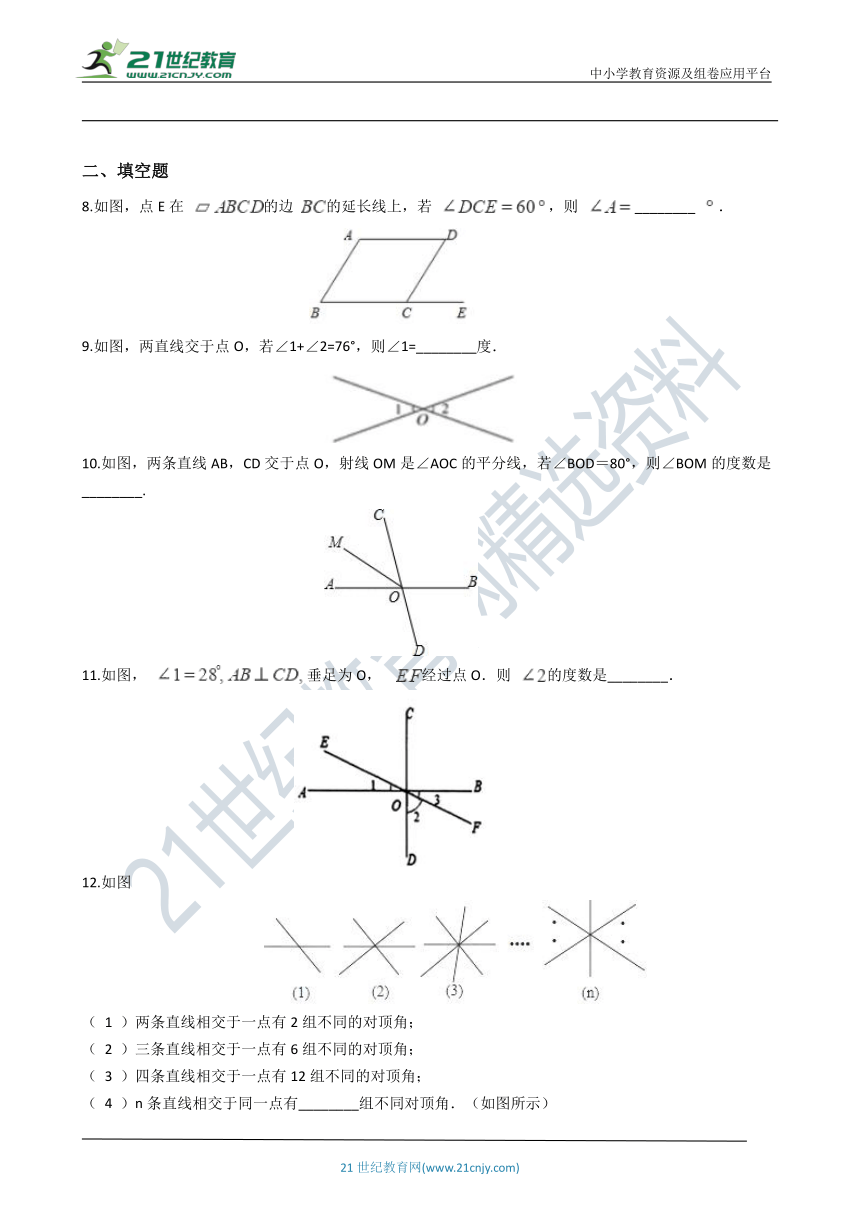
二、填空题
8.如图,点E在 的边 的延长线上,若 ,则 ________ .
9.如图,两直线交于点O,若∠1+∠2=76°,则∠1=________度.
10.如图,两条直线AB,CD交于点O,射线OM是∠AOC的平分线,若∠BOD=80°,则∠BOM的度数是________.
11.如图, 垂足为O, 经过点O.则 的度数是________.
12.如图
( 1 )两条直线相交于一点有2组不同的对顶角;
( 2 )三条直线相交于一点有6组不同的对顶角;
( 3 )四条直线相交于一点有12组不同的对顶角;
( 4 )n条直线相交于同一点有________组不同对顶角.(如图所示)
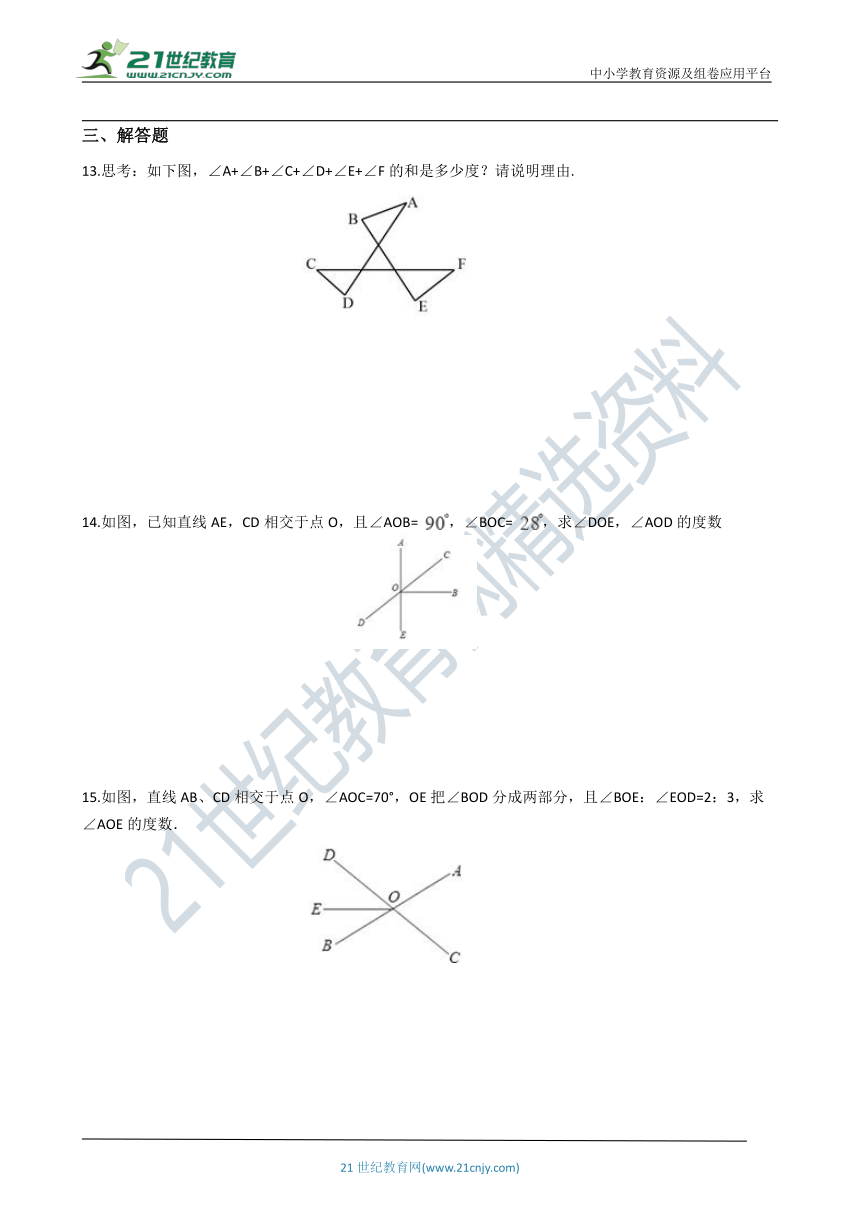
三、解答题
13.思考:如下图,∠A+∠B+∠C+∠D+∠E+∠F的和是多少度?请说明理由.
14.如图,已知直线AE,CD相交于点O,且∠AOB= ,∠BOC= ,求∠DOE,∠AOD的度数
15.如图,直线AB、CD相交于点O,∠AOC=70°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,求∠AOE的度数.
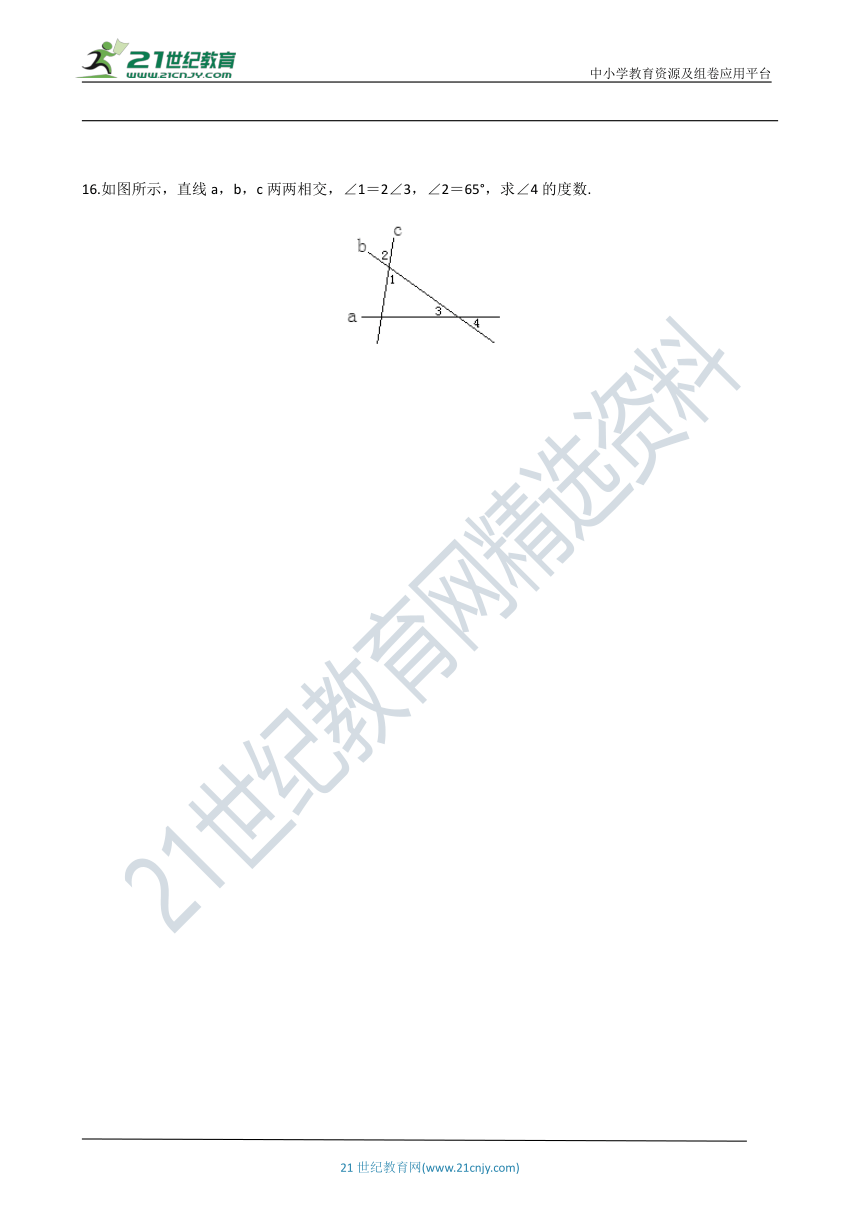
16.如图所示,直线a,b,c两两相交,∠1=2∠3,∠2=65°,求∠4的度数.
答案解析部分
一、单选题
1.【答案】 B
【解析】解:A、 不一定成立,此项不符题意;
B、由对顶角相等得: 一定成立,此项符合题意;
C、 不一定成立,此项不符题意;
D、 不一定成立,此项不符题意;
故答案为:B.
2.【答案】 D
【解析】解:A、图中∠1和∠2不是对顶角,故A不符合题意;
B、图中∠1和∠2不是对顶角,B故A不符合题意;
C、图中∠1和∠2不是对顶角,故C不符合题意;
D、图中∠1和∠2是对顶角,故D不符合题意;
故答案为:D.
3.【答案】 A
【解析】解:直线m、n相交,则∠1与∠2互为邻补角.
故答案为:A.
4.【答案】 C
【解析】A、相等的角不一定是对顶角,此项是假命题;
B、一个角的补角不一定大于这个角,如这个角为 ,其补角为 ,小于这个角,此项是假命题;
C、由绝对值的非负性得:绝对值最小的数是0,此项是真命题;
D、如果 ,那么 或 ,此项是假命题;
故答案为:C.
5.【答案】 D
【解析】解:∵∠A=∠C=90°,∠AEB=∠GED
∴∠1=∠2=25°
故答案为:D.
6.【答案】 C
【解析】解:∵∠BOC=60°,∴∠AOC=180°-∠BOC=120°.
故答案为:C.
7.【答案】 B
【解析】每两条直线相交构成2对对顶角,三条直线两两相交构成 对对顶角,故选B.
二、填空题
8.【答案】 120
【解析】解: ,
,
四边形 是平行四边形,
,
故答案为:120.
9.【答案】 38
【解析】解:∵两直线交于点O,
∴∠1=∠2,
∵∠1+∠2=76°,
∴∠1=38°.
故答案为:38.
10.【答案】 140°
【解析】解:∵∠BOD=80°,
∴∠AOC=80°,∠COB=100°,
∵射线OM是∠AOC的平分线,
∴∠COM=40°,
∴∠BOM=40°+100°=140°,
故答案为:140°.
11.【答案】 62?
【解析】解:∵AB⊥CD ,
∴∠BOD=90°,
∵∠3=∠1=28°,
∴∠2=90°-∠3=62°.
故答案为:62°.
12.【答案】 n(n-1)
【解析】观察图形可知,n条直线相交于同一点有(1+2+…+n-1)×2= ×2=n(n-1)组不同对顶角.故答案为:n(n-1).
三、解答题
13.【答案】 解:∠A+∠B+∠C+∠D+∠E+∠F=360°,理由如下
如下图所示
由三角形的内角和定理可得:∠A+∠B+∠AGB=180°①,∠C+∠D+∠CMD=180°②,∠E+∠F+∠ENF=180°③,∠GMN+∠MNG+∠MGN=180°
①+②+③,得
∠A+∠B+∠AGB+∠C+∠D+∠CMD+∠E+∠F+∠ENF=540°
∵∠AGB=∠MGN,∠CMD=∠GMN,∠ENF=∠MNG
∴∠A+∠B+∠C+∠D+∠E+∠F=540°-(∠CMD+∠ENF+∠AGB)
=540°-(∠GMN+∠MNG+∠MGN)
=360°
【解析】根据三角形的内角和定理可得:∠A+∠B+∠AGB=180°①,∠C+∠D+∠CMD=180°②,∠E+∠F+∠ENF=180°③,∠GMN+∠MNG+∠MGN=180°,然后将①+②+③,并利用对顶角相等和等量代换即可得出结论.
14.【答案】 解:∵∠AOB=90°,∠BOC=28°,
∴∠AOC=∠AOB﹣∠BOC=62°,
∴∠DOE=∠AOC=62°,
∴∠AOD=180°﹣∠DOE=118°.
【解析】先求出∠AOC=∠AOB﹣∠BOC=62°,再根据对顶角相等得出∠DOE=∠AOC=62°,然后根据邻补角定义求出∠AOD .
15.【答案】 解:∵∠AOC=70°,
∴∠BOD=∠AOC=70°,
∵∠BOE:∠EOD=2:3,
∴∠BOE= ×70°=28°,
∴∠AOE=180°-28°=152°.
【解析】根据对顶角相等求出∠BOD的度数,再根据∠BOE:∠EOD=2:3求出∠BOE的度数,然后利用互为邻补角的两个角的和等于180°即可求出∠AOE的度数.
16.【答案】 解:∵∠1=∠2,∠1=2∠3
∴∠2=2∠3
又∵∠3=∠4,
∴∠2=2∠4
∵∠2=65°
∴∠4=32.5°.
【解析】根据对顶角的性质,∠1=∠2,∠3=∠4,再根据∠1=2∠3,∠2=65°,可得∠4的度数.
一、单选题
1.下列四个图中, 一定成立的是(????? )
A.????????????????????B.????????????????????C.????????????????????D.?
2.下面四个图形中, 与 是对顶角的是(?? )
A.?????????????B.?????????????C.?????????????D.?
3.如图,直线m、n相交,则∠1与∠2的位置关系为( )
A.?邻补角???????????????????????????????B.?内错角???????????????????????????????C.?同旁内角???????????????????????????????D.?对顶角
4.下列命题中,属于真命题的是(?? )
A.?相等的角是对顶角??????????????????????????????????????????????B.?一个角的补角大于这个角
C.?绝对值最小的数是0????????????????????????????????????????????D.?如果 ,那么a=b
5.如图,∠A=∠C=90°,AD、BC交于点E,∠2=25°,则∠1的值为( ???)
A.?55°???????????????????????????????????????B.?35°???????????????????????????????????????C.?45°???????????????????????????????????????D.?25°
6.如图,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是(???? )
A.?60°?????????????????????????????????????B.?90°?????????????????????????????????????C.?120°?????????????????????????????????????D.?150°
7.平面上三条直线两两相交最多能构成对顶角的对数是(????? ).
A.?7???????????????????????????????????????????B.?6???????????????????????????????????????????C.?5???????????????????????????????????????????D.?4
二、填空题
8.如图,点E在 的边 的延长线上,若 ,则 ________ .
9.如图,两直线交于点O,若∠1+∠2=76°,则∠1=________度.
10.如图,两条直线AB,CD交于点O,射线OM是∠AOC的平分线,若∠BOD=80°,则∠BOM的度数是________.
11.如图, 垂足为O, 经过点O.则 的度数是________.
12.如图
( 1 )两条直线相交于一点有2组不同的对顶角;
( 2 )三条直线相交于一点有6组不同的对顶角;
( 3 )四条直线相交于一点有12组不同的对顶角;
( 4 )n条直线相交于同一点有________组不同对顶角.(如图所示)
三、解答题
13.思考:如下图,∠A+∠B+∠C+∠D+∠E+∠F的和是多少度?请说明理由.
14.如图,已知直线AE,CD相交于点O,且∠AOB= ,∠BOC= ,求∠DOE,∠AOD的度数
15.如图,直线AB、CD相交于点O,∠AOC=70°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,求∠AOE的度数.
16.如图所示,直线a,b,c两两相交,∠1=2∠3,∠2=65°,求∠4的度数.
答案解析部分
一、单选题
1.【答案】 B
【解析】解:A、 不一定成立,此项不符题意;
B、由对顶角相等得: 一定成立,此项符合题意;
C、 不一定成立,此项不符题意;
D、 不一定成立,此项不符题意;
故答案为:B.
2.【答案】 D
【解析】解:A、图中∠1和∠2不是对顶角,故A不符合题意;
B、图中∠1和∠2不是对顶角,B故A不符合题意;
C、图中∠1和∠2不是对顶角,故C不符合题意;
D、图中∠1和∠2是对顶角,故D不符合题意;
故答案为:D.
3.【答案】 A
【解析】解:直线m、n相交,则∠1与∠2互为邻补角.
故答案为:A.
4.【答案】 C
【解析】A、相等的角不一定是对顶角,此项是假命题;
B、一个角的补角不一定大于这个角,如这个角为 ,其补角为 ,小于这个角,此项是假命题;
C、由绝对值的非负性得:绝对值最小的数是0,此项是真命题;
D、如果 ,那么 或 ,此项是假命题;
故答案为:C.
5.【答案】 D
【解析】解:∵∠A=∠C=90°,∠AEB=∠GED
∴∠1=∠2=25°
故答案为:D.
6.【答案】 C
【解析】解:∵∠BOC=60°,∴∠AOC=180°-∠BOC=120°.
故答案为:C.
7.【答案】 B
【解析】每两条直线相交构成2对对顶角,三条直线两两相交构成 对对顶角,故选B.
二、填空题
8.【答案】 120
【解析】解: ,
,
四边形 是平行四边形,
,
故答案为:120.
9.【答案】 38
【解析】解:∵两直线交于点O,
∴∠1=∠2,
∵∠1+∠2=76°,
∴∠1=38°.
故答案为:38.
10.【答案】 140°
【解析】解:∵∠BOD=80°,
∴∠AOC=80°,∠COB=100°,
∵射线OM是∠AOC的平分线,
∴∠COM=40°,
∴∠BOM=40°+100°=140°,
故答案为:140°.
11.【答案】 62?
【解析】解:∵AB⊥CD ,
∴∠BOD=90°,
∵∠3=∠1=28°,
∴∠2=90°-∠3=62°.
故答案为:62°.
12.【答案】 n(n-1)
【解析】观察图形可知,n条直线相交于同一点有(1+2+…+n-1)×2= ×2=n(n-1)组不同对顶角.故答案为:n(n-1).
三、解答题
13.【答案】 解:∠A+∠B+∠C+∠D+∠E+∠F=360°,理由如下
如下图所示
由三角形的内角和定理可得:∠A+∠B+∠AGB=180°①,∠C+∠D+∠CMD=180°②,∠E+∠F+∠ENF=180°③,∠GMN+∠MNG+∠MGN=180°
①+②+③,得
∠A+∠B+∠AGB+∠C+∠D+∠CMD+∠E+∠F+∠ENF=540°
∵∠AGB=∠MGN,∠CMD=∠GMN,∠ENF=∠MNG
∴∠A+∠B+∠C+∠D+∠E+∠F=540°-(∠CMD+∠ENF+∠AGB)
=540°-(∠GMN+∠MNG+∠MGN)
=360°
【解析】根据三角形的内角和定理可得:∠A+∠B+∠AGB=180°①,∠C+∠D+∠CMD=180°②,∠E+∠F+∠ENF=180°③,∠GMN+∠MNG+∠MGN=180°,然后将①+②+③,并利用对顶角相等和等量代换即可得出结论.
14.【答案】 解:∵∠AOB=90°,∠BOC=28°,
∴∠AOC=∠AOB﹣∠BOC=62°,
∴∠DOE=∠AOC=62°,
∴∠AOD=180°﹣∠DOE=118°.
【解析】先求出∠AOC=∠AOB﹣∠BOC=62°,再根据对顶角相等得出∠DOE=∠AOC=62°,然后根据邻补角定义求出∠AOD .
15.【答案】 解:∵∠AOC=70°,
∴∠BOD=∠AOC=70°,
∵∠BOE:∠EOD=2:3,
∴∠BOE= ×70°=28°,
∴∠AOE=180°-28°=152°.
【解析】根据对顶角相等求出∠BOD的度数,再根据∠BOE:∠EOD=2:3求出∠BOE的度数,然后利用互为邻补角的两个角的和等于180°即可求出∠AOE的度数.
16.【答案】 解:∵∠1=∠2,∠1=2∠3
∴∠2=2∠3
又∵∠3=∠4,
∴∠2=2∠4
∵∠2=65°
∴∠4=32.5°.
【解析】根据对顶角的性质,∠1=∠2,∠3=∠4,再根据∠1=2∠3,∠2=65°,可得∠4的度数.
