第二册第六章圆周运动 单元检测 word版含答案
文档属性
| 名称 | 第二册第六章圆周运动 单元检测 word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 616.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-17 08:21:03 | ||
图片预览




文档简介
圆 周 运 动
1.对于物体做匀速圆周运动,下列说法中正确的是( )
A.其转速与角速度成反比,其周期与角速度成正比
B.运动的快慢可用线速度描述,也可用角速度来描述
C.匀速圆周运动的速度保持不变
D.做匀速圆周运动的物体,其加速度保持不变
2.如图所示,摩天轮悬挂的座舱在竖直平面内做匀速圆周运动。座舱的质量为m,运动半径为R,角速度大小为ω,重力加速度为g,则座舱 ( )
A.运动周期为
B.线速度的大小为ωR
C.受摩天轮作用力的大小始终为mg
D.受摩天轮作用力的大小始终为mω2R
3.如图所示,转动自行车的脚踏板时,关于大齿轮、小齿轮、后轮边缘上的A、B、C三点的向心加速度的说法正确的是 ( )
A.A点的向心加速度比B点的大
B.B点的向心加速度比C点的大
C.C点的向心加速度最大
D.以上三种说法都不正确
4.(2019·浙江1月学考)如图所示,四辆相同的小“自行车”固定在四根水平横杆上,四根杆子间的夹角均保持90°不变,且可一起绕中间的竖直轴转动。当小“自行车”的座位上均坐上小孩并一起转动时,他们的 ( )
A.角速度相同 B.线速度相同
C.向心加速度相同 D.所需向心力大小相同
5.如图,(d和c共轴)靠轮传动装置中右轮半径为2r,a为它边缘上的一点,b为轮上的一点、距轴为r;左侧为一轮轴,大轮的半径为4r,d为它边缘上的一点;小轮半径为r,c为它边缘上的一点。若传动中靠轮不打滑,则下列说法错误的是
( )
A.a点与d点的向心加速度大小之比为1∶4
B.a点与c点的线速度之比为1∶1
C.c点与b点的角速度之比为2∶1
D.b点与d点的周期之比为2∶1
6.图示为锥形齿轮的传动示意图,大齿轮带动小齿轮转动,大、小齿轮的角速度大小分别为ω1、ω2,两齿轮边缘处的线速度大小分别为v1、v2,则 ( )
A.ω1=ω2,v1>v2 B.ω1>ω2,v1=v2
C.ω1<ω2,v1=v2 D.ω1=ω2,v17.公园里的“飞天秋千”游戏开始前,座椅由钢丝绳竖直悬吊在半空。秋千匀速转动时,绳与竖直方向成某一角度,其简化模型如图所示。若要使夹角θ变大,可 ( )
A.增大转动周期 B.将钢丝绳变短
C.增大座椅质量 D.增大角速度
8.A、B、C三个物体放在旋转圆台上,它们由相同材料制成,A的质量为2m,B、C的质量各为m。如果OA=OB=R,OC=2R,则当圆台旋转时(设A、B、C都没有滑动),下述结论中错误的是 ( )
A.物体C向心加速度最大
B.物体B静摩擦力最小
C.当圆台旋转转速增加时,C比B先开始滑动
D.当圆台旋转转速增加时,A比B先开始滑动
9.盛有质量为m的水的小桶,以手臂为半径使之在竖直平面内做圆周运动,水随桶转到最高点需要的向心力为mω2R,则 ( )
A.当mω2R>mg时水就会洒出来
B.当mω2RC.当mω2R=mg时水刚好不会洒出来
D.以上结论都不对
10.如图所示,质量m=2.0×104 kg的汽车以不变的速率先后驶过凹形桥与凸形桥面,两桥面的圆弧半径均为60 m,如果桥面承受的压力不超过3.0×105 N,g取
10 m/s2,则汽车允许的最大速率是 ( )
A.10 m/s B.10 m/s
C.30 m/s D.10 m/s
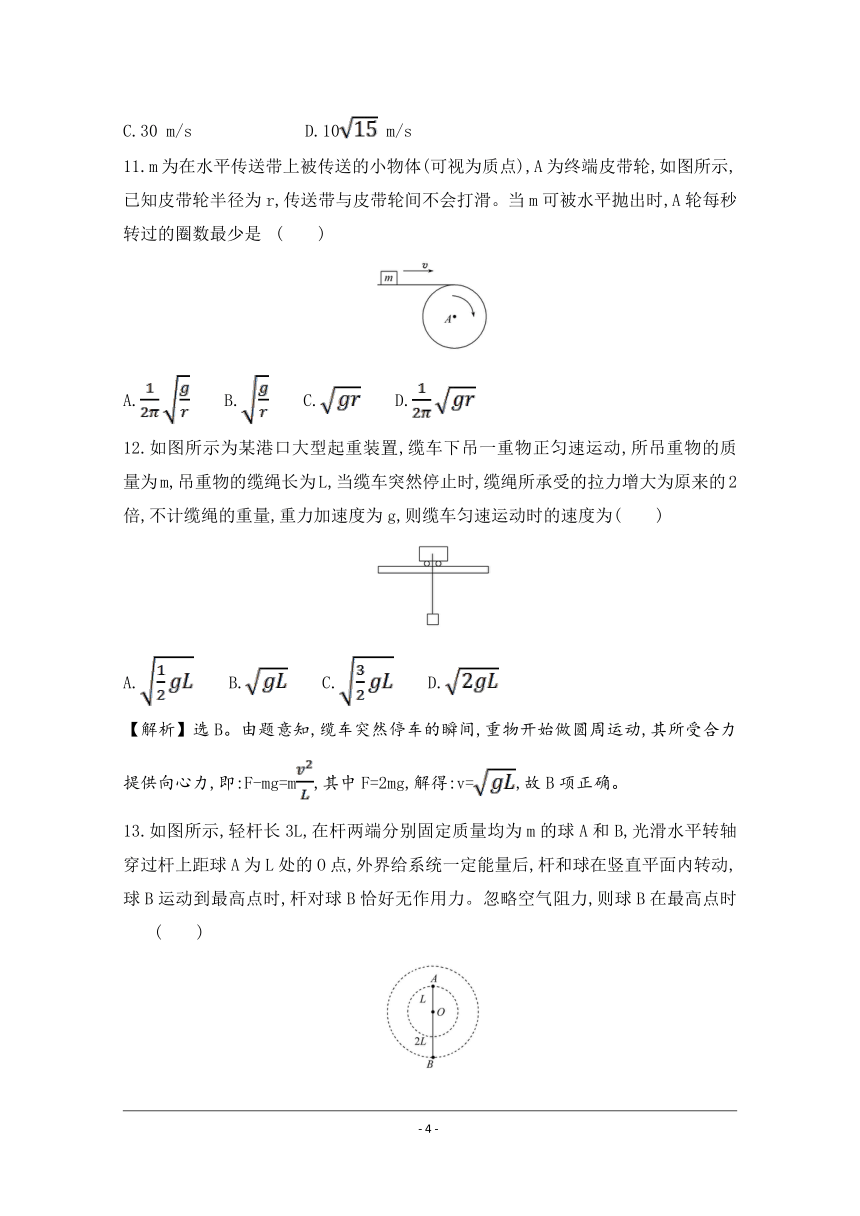
11.m为在水平传送带上被传送的小物体(可视为质点),A为终端皮带轮,如图所示,已知皮带轮半径为r,传送带与皮带轮间不会打滑。当m可被水平抛出时,A轮每秒转过的圈数最少是 ( )
A. B. C. D.
12.如图所示为某港口大型起重装置,缆车下吊一重物正匀速运动,所吊重物的质量为m,吊重物的缆绳长为L,当缆车突然停止时,缆绳所承受的拉力增大为原来的2倍,不计缆绳的重量,重力加速度为g,则缆车匀速运动时的速度为( )
A. B. C. D.
【解析】选B。由题意知,缆车突然停车的瞬间,重物开始做圆周运动,其所受合力提供向心力,即:F-mg=m,其中F=2mg,解得:v=,故B项正确。
13.如图所示,轻杆长3L,在杆两端分别固定质量均为m的球A和B,光滑水平转轴穿过杆上距球A为L处的O点,外界给系统一定能量后,杆和球在竖直平面内转动,球B运动到最高点时,杆对球B恰好无作用力。忽略空气阻力,则球B在最高点时 ( )
A.球B的速度大小为零
B.球A的速度大小为
C.水平转轴对杆的作用力为1.5mg
D.水平转轴对杆的作用力为2.5mg
14.(5分)用如图所示的装置可以做“探究向心力的大小与质量m、角速度ω和半径r之间的关系”实验。
(1)本实验采用的科学方法是____________。?
(2)转动手柄使长槽和短槽分别随变速塔轮匀速转动,槽内的球就做匀速圆周运动,横臂的挡板对球的压力提供了小球做匀速圆周运动的向心力,弹簧测力筒上露出的标尺可以显示此力的大小。由图示情景可知,钢球A与铝球B的角速度关系为ωA________(选填“>”“=”或“<”)ωB。?
(3)由该实验装置可以得到的结论是________。?
A.在质量和半径一定的情况下,向心力的大小与角速度成正比
B.在质量和半径一定的情况下,向心力的大小与线速度的大小成正比
C.在半径和角速度一定的情况下,向心力的大小与质量成正比
D.在质量和角速度一定的情况下,向心力的大小与半径成反比
15.(9分)在“用圆锥摆验证向心力的表达式”实验中,如图甲所示,细绳的悬点刚好与一竖直放置的刻度尺零刻度线对齐。将画着几个同心圆的白纸置于水平桌面上,使钢球静止时刚好位于圆心。用手带动钢球,调整白纸的位置,设法使钢球刚好沿纸上某个半径为r的圆做圆周运动,钢球的质量为m,重力加速度为g。
(1)用停表记录运动n圈的总时间为t,那么钢球做圆周运动需要的向心力表达式为Fn=______________。?
(2)通过刻度尺测得钢球运动轨道平面距悬点的高度为h,那么钢球做圆周运动中外力提供的向心力表达式为F=______________;?
(3)改变钢球做圆周运动的半径,多次实验,得到如图乙所示的-h关系图像为一直线时,可以达到粗略验证向心力表达式的目的,该图线的斜率表达式为k=__________。?
16.如图所示,水平转盘上放有质量为m的物体(可视为质点),连接物体和转轴的绳子长为r,物体与转盘间的最大静摩擦力是其压力的μ倍,转盘的角速度由零逐渐增大,求:
(1)绳子对物体的拉力为零时的最大角速度。
(2)当角速度为时,绳子对物体拉力的大小。
17.(9分)如图所示,半径为R,内径很小的光滑半圆管竖直放置,两个质量均为m的小球A、B以不同速率进入管内,A通过最高点C时,对管壁上部的压力为3mg,B通过最高点C时,对管壁下部的压力为0.75mg。求A、B两球落地点间的距离。
18.(4分)如图所示,长为L的轻质硬杆,一端固定一个质量为m的小球,另一端固定在水平转轴上,现让杆绕转轴O在竖直平面内匀速转动,转动的角速度为ω,某时刻杆对球的作用力恰好与杆垂直,则此时杆与水平面的夹角θ为( )
A.sinθ= B.sinθ=
C.cosθ= D.cosθ=
19.(4分)(2020·邵阳高一检测)如图所示,半径为R的半球形容器固定在水平转台上,转台绕过容器球心O的竖直轴线以角速度ω匀速转动。质量不同的小物块A、B随容器转动且相对容器壁静止,A、B和球心O点连线与竖直方向的夹角分别为α和β,α>β。则 ( )
A.A的质量一定小于B的质量
B.A、B受到的摩擦力可能同时为零
C.若A不受摩擦力,则B受沿容器壁向上的摩擦力
D.若ω增大,A、B受到的摩擦力可能都增大
20.(4分)(多选)如图所示,一个固定在竖直平面上的光滑半圆形管道,管道里有一个直径略小于管道内径的小球,小球在管道内做圆周运动,从B点脱离后做平抛运动,经过0.3 s后又恰好垂直与倾角为45°的斜面相碰。已知半圆形管道的半径为R=1 m,小球可看作质点且其质量为m=1 kg,g取10 m/s2。则 ( )
A.小球在斜面上的相碰点C与B的水平距离为0.45 m
B.小球在斜面上的相碰点C与B的水平距离为 0.9 m
C.小球经过管道的B点时,小球对管道有向下的作用力
D.小球经过管道的B点时,受到管道的作用力大小为1 N
21.(5分)如图所示为改装的探究圆周运动的向心加速度的实验装置。有机玻璃支架上固定一个直流电动机,电动机转轴上固定一个半径为r的塑枓圆盘,圆盘中心正下方用细线接一个重锤,圆盘边缘连接细绳,细绳另一端连接一个小球。实验操作如下:
①利用天平测量小球的质量m,记录当地的重力加速度g的大小;
②闭合电源开关,让小球做如图所示的匀速圆周运动,调节激光笔2的高度和激光笔1的位置,让激光恰好照射到小球的中心,用刻度尺测量小球做圆周运动的半径R和球心到塑料圆盘的高度h;
③当小球第一次到达A点时开始计时,并记录为1次,记录小球n次到达A点的时间t;
④切断电源,整理器材。
请回答下列问题:
(1)(多选)下列说法正确的是________。?
A.小球运动的周期为
B.小球运动的线速度大小为
C.小球运动的向心力大小为
D.若电动机转速增加,激光笔1、2应分别左移、升高
(2)若已测出R=40.00 cm、r=4.00 cm,h=90.00 cm,t=100.00 s,n=51,π取3.14,则小球做圆周运动的周期T=________s,记录的当地重力加速度大小应为g=______m/s2。(计算结果均保留3位有效数字) ?
22.(13分)(2020·沈阳高一检测)如图所示,装置BO′O可绕竖直轴O′O转动,可视为质点的小球A与两细线连接后分别系于B、C两点,装置静止时细线AB水平,细线AC与竖直方向的夹角θ=37°。已知小球的质量m=1 kg,细线AC长l=
1 m,B点距C点的水平和竖直距离相等。(重力加速度g取10 m/s2,sin37°
=,cos37°=)
(1)若装置匀速转动的角速度为ω1时,细线AB上的张力为零而细线AC与竖直方向夹角仍为37°,求角速度ω1的大小;
(2)若装置匀速转动的角速度ω2= rad/s,求细线AC与竖直方向的夹角;
(3)装置可以以不同的角速度匀速转动,试通过计算讨论细线AC上张力T随ω2的变化关系(请用m、l和ω表示)。
1.【解析】选B。根据T=可知,周期与角速度成反比,故A项错误;角速度是描述匀速圆周运动速度方向变化快慢的物理量,线速度表示单位时间内转过的弧长,都可以描述运动的快慢,故B正确;匀速圆周运动的过程中,线速度的大小不变,但方向改变,所以线速度改变,故C项错误;向心加速度方向始终指向圆心,是个变量,故D项错误。
2.【解析】选B。根据角速度和周期的关系可知,周期T=,故A项错误;线速度大小v=ωR,故B项正确;座舱做匀速圆周运动,受到的合外力充当向心力,故合力大小F=mω2R,由于座舱所受合外力为重力与摩天轮对座舱的作用力的合力,故摩天轮对座舱的作用力不等于mg,也不等于mω2R,故C、D错误。
3.【解析】选C。A、B为皮带传动,所以线速度相等,则由向心加速度公式an=,又因A的半径大于B的半径,可知,A的向心加速度小于B的向心加速度,故A项错误;B与C绕同一转轴转动,角速度相等,根据an=ω2r可知半径大的向心加速度大,则C的向心加速度大,故B项错误;由以上分析可知,C点的向心加速度最大,故C项正确,D项错误。
4.【解析】选A。四辆小“自行车”属于同轴转动,所以“自行车”上的每个小孩的角速度相同,A正确;线速度是矢量,各个小孩的线速度方向不同,所以线速度不同,B错误;向心加速度指向圆心,所以每个小孩的向心加速度方向不同,C错误;由于每个小孩的质量可能不同,所以其所需的向心力大小可能不同,D错误。
5.【解析】选A。ωc=2ωa、ωc=ωd,则ωd=2ωa;又ra=2r、rd=4r;据a=rω2可得,ad=8aa,故A错误;小轮与右轮间靠摩擦传动不打滑,两轮边缘上点的线速度大小相等,即va=vc,故B正确;va=vc、ra=2r、rc=r,据ω=可得,ωc=2ωa;a、b两点均在右轮上,ωa=ωb;所以ωc=2ωb,故C正确;大轮与小轮同轴转动,则ωc=ωd;又ωc=2ωb,所以ωd=2ωb。据T=可得,Tb=2Td,故D正确。
6.【解析】选C。大齿轮带动小齿轮转动,轮子边缘上的点在相同时间内走过的弧长相同,则线速度大小相等,即v1= v2,根据ω=知,r1>r2,则ω1<ω2,故C项正确。
7.【解析】选D。对座椅进行受力分析,如图
座椅所受重力和拉力的合力提供向心力,
mgtanθ=m(lsinθ+r)
解得l=-,
则要使夹角变大,可减小周期,或使钢丝绳的长度变长,或增大角速度,与座椅的质量无关,故D项正确,A、B、C错误。
8【解析】选D。三个物体都做匀速圆周运动,角速度相等,向心加速度an=ω2r,可见,半径越大,向心加速度越大,所以物体C的向心加速度最大,A正确;三个物体的合力都指向圆心,对任意一个受力分析,如图
支持力与重力平衡,由静摩擦力f提供向心力,则得
f=Fn。
根据题意,rC=2rA=2rB=2R
由向心力公式Fn=mω2r,
得三个物体所受的静摩擦力分别为:fA=(2m)ω2R=2mω2R,fB=mω2R。
fC=mω2(2R)=2mω2R,
故物体B受到的静摩擦力最小,B正确;当ω变大时,所需要的向心力也变大,当达到最大静摩擦力时,物体开始滑动。当转速增加时,A、C所需向心力同步增加,且保持相等。B所需向心力也增加,A和C所需的向心力与B所需的向心力保持2∶1的关系。由于B和C受到的最大静摩擦力始终相等,都比A小,所以C先滑动,A和B后同时滑动,C正确,D错误,本题选错误的,故选D。
9.【解析】选C。设小桶转到最高点时水恰好不从桶里流出来时,小桶的角速度为ω,则由牛顿第二定律得mg=mω2R,当mω2R>mg时,桶对水有向下的作用力,此时水不会洒出来,故C项正确。
10.【解析】选A。相同速率下汽车在最低点受到的支持力最大,即此时的最大速度就是全程允许的最大速率,根据FN1-mg=m,即v==10 m/s。由于v<=10 m/s,故在凸形桥最高点上汽车不会脱离桥面,所以汽车允许的最大速率为10 m/s,故A项正确。
11.【解析】选A。物体恰好不被抛出的临界条件是最高点重力恰好提供向心力,根据牛顿第二定律,有:mg=m,根据线速度定义公式有:v=2πrn,联立解得:n=,故A项正确。
12.【解析】选B。由题意知,缆车突然停车的瞬间,重物开始做圆周运动,其所受合力提供向心力,即:F-mg=m,其中F=2mg,解得:v=,故B项正确。
13.【解析】选C。球B运动到最高点时,杆对球B恰好无作用力,即重力恰好提供向心力,有mg=m,解得v=,故A错误;由于A、B两球的角速度相等,则球A的速度大小v′=,故B错误;球B到最高点时,对杆无弹力,此时球A受重力和拉力的合力提供向心力,有F-mg=m,解得:F=1.5mg,故C正确,D错误。
14.【解析】(1)在研究向心力的大小Fn与质量m、角速度ω和半径r之间的关系时,需先控制某些量不变,研究另外两个物理量的关系,该方法为控制变量法。
(2)由图可知图中两球受到的向心力相等,转动的半径相同,由于铝的密度小,则相同大小的铝球的质量小,由向心力的公式:Fn=mω2r,则ωA<ωB。
(3)选C。在质量和半径一定的情况下,向心力的大小与角速度平方成正比,故A项错误;图示的装置不能显示线速度的大小,故B项错误;在半径和角速度一定的情况下,向心力的大小与质量成正比,故C项正确;在质量和角速度一定的情况下,向心力的大小与半径成正比,故D项错误。
答案:(1)控制变量法 (2)< (3)C
15.【解析】(1)根据向心力公式:Fn=m ,而v= ,T=
得:Fn=mr。
(2)如图由几何关系可得:Fn=mgtanθ=mg。
(3)由上面分析得:mg=mr,整理得:=·h ,斜率表达式为:。
答案:(1)mr (2)mg (3)
16.【解析】(1)当恰由最大静摩擦力提供向心力时,绳子拉力为零且角速度达到最大,设转盘转动的角速度为ω0,则由μmg=mr (2分)
得ω0=。 (2分)
(2)当ω=时,ω>ω0,所以绳子的拉力F和最大静摩擦力共同提供向心力,此时,
F+μmg=mω2r (2分)
代入数据得F=μmg。 (2分)
答案:(1) (2)μmg
17.【解析】两个小球离开轨道后均做平抛运动,竖直方向上运动情况相同。
根据2R=gt2,可得t=2 (1分)
在最高点时,两小球受重力和管壁的作用力,这两个力的合力作为向心力,
对A球:3mg+mg=m (1分)
解得:vA=2, (1分)
则sA= vAt=4R (1分)
对B球:mg-0.75mg=m (2分)
解得:vB=, (1分)
则sB= vBt=R (1分)
A、B两球落地点间的距离等于它们平抛运动的水平位移之差,
则有:sA-sB=3R (1分)
即A、B两球落地点间的距离为3R。
答案:3R
18.【解析】选A。小球所受重力和杆的作用力的合力提供向心力,根据牛顿第二定律有:mgsinθ=mω2L,解得:sinθ=,故A项正确。
19.【解析】选D。根据题目条件无法确定A的质量和B的质量的大小,故A项错误;以A为研究对象,假设不受摩擦力,A受到重力和支持力,合力提供向心力,设此时对应的角速度为ωA,根据牛顿第二定律可得mAgtanα=mArA,其中rA=Rsinα,则ωA=,同理可得当B的摩擦力为零时,角速度为:ωB=;由于α>β,故A、B受到的摩擦力不可能同时为零,故B项错误;若A不受摩擦力,整体转动的角速度为:ωA=>ωB=,则B有向上的运动趋势,故B受沿容器壁向下的摩擦力,故C项错误;若转动的角速度ω>ωA,A和B受沿容器壁向下的摩擦力,如果角速度增大,则A、B受到的摩擦力都增大,故D项正确。
20.【解析】选B、C、D。小球从B到C的运动时间为t=0.3 s,那么,小球在C点的竖直分速度为:vy=gt=3 m/s。由小球恰好垂直与倾角为45°的斜面相碰可知水平分速度为:v==3 m/s,故小球在斜面上的相碰点C与B点的水平距离为:s=vt=0.9 m,故B项正确,A项错误;对小球在B点应用牛顿第二定律可得:FN+mg=m=9 N,所以,FN=-1 N,即管道对小球的支持力为1 N,方向竖直向上;由牛顿第三定律可得:小球经过管道的B点时,小球对管道的作用力大小为1 N,方向竖直向下,故C、D项正确。
21.?【解析】(1)从小球第1次到第n次通过A位置,
转动圈数为n-1,时间为t,故周期为:T=,故A错误;小球的线速度大小为:v==,故B正确;小球受重力和拉力,合力提供向心力,设绳与竖直方向的夹角为α,则:Tcosα=mg
Tsinα=F向
故F向=mgtanα=mg,故C错误;
若电动机的转速增加,则转动半径增加,故激光笔1、2应分别左移、上移,故D正确;故选B、D。
(2)小球做圆周运动的周期
T== s=2.00 s;
向心力:F向=mg=mR
解得:g==9.86 m/s2
答案:(1)B、D (2)2.00 9.86
22【解析】(1)细线AB上张力恰为零时有
mgtan37°=mlsin37°, (2分)
解得ω1== rad/s。 (1分)
(2)当ω2>ω1时, 细线AB应松弛,即
mgtanθ′=mlsinθ′, (2分)
解得cosθ′=,θ′=53°。
此时细线AB恰好竖直,但张力为零。 (1分)
(3)当ω<ω1时,细线AB水平,细线AC上张力的竖直分量等于小球的重力:
Tcosθ=mg, (2分)
解得T==12.5 N; (1分)
当ω1<ω<ω2时,细线AB松弛,细线AC上张力的水平分量等于小球做圆周运动需要的向心力
Tsinθ′=mω2lsinθ′, (1分)
T=mω2l。 (1分)
当ω>ω2时,细线AB在竖直方向绷直,仍然由细线AC上张力的水平分量提供小球做圆周运动需要的向心力Tsinθ′=mω2lsinθ′, (1分)
T=mω2l。 (1分)
综上所述:当ω<ω1时,T=12.5 N不变;
当ω>ω1时,T=mω2l。
答案:(1) rad/s (2)53°
(3)当ω<ω1时,T=12.5 N不变;当ω>ω1时,T=mω2l
- 1 -
1.对于物体做匀速圆周运动,下列说法中正确的是( )
A.其转速与角速度成反比,其周期与角速度成正比
B.运动的快慢可用线速度描述,也可用角速度来描述
C.匀速圆周运动的速度保持不变
D.做匀速圆周运动的物体,其加速度保持不变
2.如图所示,摩天轮悬挂的座舱在竖直平面内做匀速圆周运动。座舱的质量为m,运动半径为R,角速度大小为ω,重力加速度为g,则座舱 ( )
A.运动周期为
B.线速度的大小为ωR
C.受摩天轮作用力的大小始终为mg
D.受摩天轮作用力的大小始终为mω2R
3.如图所示,转动自行车的脚踏板时,关于大齿轮、小齿轮、后轮边缘上的A、B、C三点的向心加速度的说法正确的是 ( )
A.A点的向心加速度比B点的大
B.B点的向心加速度比C点的大
C.C点的向心加速度最大
D.以上三种说法都不正确
4.(2019·浙江1月学考)如图所示,四辆相同的小“自行车”固定在四根水平横杆上,四根杆子间的夹角均保持90°不变,且可一起绕中间的竖直轴转动。当小“自行车”的座位上均坐上小孩并一起转动时,他们的 ( )
A.角速度相同 B.线速度相同
C.向心加速度相同 D.所需向心力大小相同
5.如图,(d和c共轴)靠轮传动装置中右轮半径为2r,a为它边缘上的一点,b为轮上的一点、距轴为r;左侧为一轮轴,大轮的半径为4r,d为它边缘上的一点;小轮半径为r,c为它边缘上的一点。若传动中靠轮不打滑,则下列说法错误的是
( )
A.a点与d点的向心加速度大小之比为1∶4
B.a点与c点的线速度之比为1∶1
C.c点与b点的角速度之比为2∶1
D.b点与d点的周期之比为2∶1
6.图示为锥形齿轮的传动示意图,大齿轮带动小齿轮转动,大、小齿轮的角速度大小分别为ω1、ω2,两齿轮边缘处的线速度大小分别为v1、v2,则 ( )
A.ω1=ω2,v1>v2 B.ω1>ω2,v1=v2
C.ω1<ω2,v1=v2 D.ω1=ω2,v1
A.增大转动周期 B.将钢丝绳变短
C.增大座椅质量 D.增大角速度
8.A、B、C三个物体放在旋转圆台上,它们由相同材料制成,A的质量为2m,B、C的质量各为m。如果OA=OB=R,OC=2R,则当圆台旋转时(设A、B、C都没有滑动),下述结论中错误的是 ( )
A.物体C向心加速度最大
B.物体B静摩擦力最小
C.当圆台旋转转速增加时,C比B先开始滑动
D.当圆台旋转转速增加时,A比B先开始滑动
9.盛有质量为m的水的小桶,以手臂为半径使之在竖直平面内做圆周运动,水随桶转到最高点需要的向心力为mω2R,则 ( )
A.当mω2R>mg时水就会洒出来
B.当mω2R
D.以上结论都不对
10.如图所示,质量m=2.0×104 kg的汽车以不变的速率先后驶过凹形桥与凸形桥面,两桥面的圆弧半径均为60 m,如果桥面承受的压力不超过3.0×105 N,g取
10 m/s2,则汽车允许的最大速率是 ( )
A.10 m/s B.10 m/s
C.30 m/s D.10 m/s
11.m为在水平传送带上被传送的小物体(可视为质点),A为终端皮带轮,如图所示,已知皮带轮半径为r,传送带与皮带轮间不会打滑。当m可被水平抛出时,A轮每秒转过的圈数最少是 ( )
A. B. C. D.
12.如图所示为某港口大型起重装置,缆车下吊一重物正匀速运动,所吊重物的质量为m,吊重物的缆绳长为L,当缆车突然停止时,缆绳所承受的拉力增大为原来的2倍,不计缆绳的重量,重力加速度为g,则缆车匀速运动时的速度为( )
A. B. C. D.
【解析】选B。由题意知,缆车突然停车的瞬间,重物开始做圆周运动,其所受合力提供向心力,即:F-mg=m,其中F=2mg,解得:v=,故B项正确。
13.如图所示,轻杆长3L,在杆两端分别固定质量均为m的球A和B,光滑水平转轴穿过杆上距球A为L处的O点,外界给系统一定能量后,杆和球在竖直平面内转动,球B运动到最高点时,杆对球B恰好无作用力。忽略空气阻力,则球B在最高点时 ( )
A.球B的速度大小为零
B.球A的速度大小为
C.水平转轴对杆的作用力为1.5mg
D.水平转轴对杆的作用力为2.5mg
14.(5分)用如图所示的装置可以做“探究向心力的大小与质量m、角速度ω和半径r之间的关系”实验。
(1)本实验采用的科学方法是____________。?
(2)转动手柄使长槽和短槽分别随变速塔轮匀速转动,槽内的球就做匀速圆周运动,横臂的挡板对球的压力提供了小球做匀速圆周运动的向心力,弹簧测力筒上露出的标尺可以显示此力的大小。由图示情景可知,钢球A与铝球B的角速度关系为ωA________(选填“>”“=”或“<”)ωB。?
(3)由该实验装置可以得到的结论是________。?
A.在质量和半径一定的情况下,向心力的大小与角速度成正比
B.在质量和半径一定的情况下,向心力的大小与线速度的大小成正比
C.在半径和角速度一定的情况下,向心力的大小与质量成正比
D.在质量和角速度一定的情况下,向心力的大小与半径成反比
15.(9分)在“用圆锥摆验证向心力的表达式”实验中,如图甲所示,细绳的悬点刚好与一竖直放置的刻度尺零刻度线对齐。将画着几个同心圆的白纸置于水平桌面上,使钢球静止时刚好位于圆心。用手带动钢球,调整白纸的位置,设法使钢球刚好沿纸上某个半径为r的圆做圆周运动,钢球的质量为m,重力加速度为g。
(1)用停表记录运动n圈的总时间为t,那么钢球做圆周运动需要的向心力表达式为Fn=______________。?
(2)通过刻度尺测得钢球运动轨道平面距悬点的高度为h,那么钢球做圆周运动中外力提供的向心力表达式为F=______________;?
(3)改变钢球做圆周运动的半径,多次实验,得到如图乙所示的-h关系图像为一直线时,可以达到粗略验证向心力表达式的目的,该图线的斜率表达式为k=__________。?
16.如图所示,水平转盘上放有质量为m的物体(可视为质点),连接物体和转轴的绳子长为r,物体与转盘间的最大静摩擦力是其压力的μ倍,转盘的角速度由零逐渐增大,求:
(1)绳子对物体的拉力为零时的最大角速度。
(2)当角速度为时,绳子对物体拉力的大小。
17.(9分)如图所示,半径为R,内径很小的光滑半圆管竖直放置,两个质量均为m的小球A、B以不同速率进入管内,A通过最高点C时,对管壁上部的压力为3mg,B通过最高点C时,对管壁下部的压力为0.75mg。求A、B两球落地点间的距离。
18.(4分)如图所示,长为L的轻质硬杆,一端固定一个质量为m的小球,另一端固定在水平转轴上,现让杆绕转轴O在竖直平面内匀速转动,转动的角速度为ω,某时刻杆对球的作用力恰好与杆垂直,则此时杆与水平面的夹角θ为( )
A.sinθ= B.sinθ=
C.cosθ= D.cosθ=
19.(4分)(2020·邵阳高一检测)如图所示,半径为R的半球形容器固定在水平转台上,转台绕过容器球心O的竖直轴线以角速度ω匀速转动。质量不同的小物块A、B随容器转动且相对容器壁静止,A、B和球心O点连线与竖直方向的夹角分别为α和β,α>β。则 ( )
A.A的质量一定小于B的质量
B.A、B受到的摩擦力可能同时为零
C.若A不受摩擦力,则B受沿容器壁向上的摩擦力
D.若ω增大,A、B受到的摩擦力可能都增大
20.(4分)(多选)如图所示,一个固定在竖直平面上的光滑半圆形管道,管道里有一个直径略小于管道内径的小球,小球在管道内做圆周运动,从B点脱离后做平抛运动,经过0.3 s后又恰好垂直与倾角为45°的斜面相碰。已知半圆形管道的半径为R=1 m,小球可看作质点且其质量为m=1 kg,g取10 m/s2。则 ( )
A.小球在斜面上的相碰点C与B的水平距离为0.45 m
B.小球在斜面上的相碰点C与B的水平距离为 0.9 m
C.小球经过管道的B点时,小球对管道有向下的作用力
D.小球经过管道的B点时,受到管道的作用力大小为1 N
21.(5分)如图所示为改装的探究圆周运动的向心加速度的实验装置。有机玻璃支架上固定一个直流电动机,电动机转轴上固定一个半径为r的塑枓圆盘,圆盘中心正下方用细线接一个重锤,圆盘边缘连接细绳,细绳另一端连接一个小球。实验操作如下:
①利用天平测量小球的质量m,记录当地的重力加速度g的大小;
②闭合电源开关,让小球做如图所示的匀速圆周运动,调节激光笔2的高度和激光笔1的位置,让激光恰好照射到小球的中心,用刻度尺测量小球做圆周运动的半径R和球心到塑料圆盘的高度h;
③当小球第一次到达A点时开始计时,并记录为1次,记录小球n次到达A点的时间t;
④切断电源,整理器材。
请回答下列问题:
(1)(多选)下列说法正确的是________。?
A.小球运动的周期为
B.小球运动的线速度大小为
C.小球运动的向心力大小为
D.若电动机转速增加,激光笔1、2应分别左移、升高
(2)若已测出R=40.00 cm、r=4.00 cm,h=90.00 cm,t=100.00 s,n=51,π取3.14,则小球做圆周运动的周期T=________s,记录的当地重力加速度大小应为g=______m/s2。(计算结果均保留3位有效数字) ?
22.(13分)(2020·沈阳高一检测)如图所示,装置BO′O可绕竖直轴O′O转动,可视为质点的小球A与两细线连接后分别系于B、C两点,装置静止时细线AB水平,细线AC与竖直方向的夹角θ=37°。已知小球的质量m=1 kg,细线AC长l=
1 m,B点距C点的水平和竖直距离相等。(重力加速度g取10 m/s2,sin37°
=,cos37°=)
(1)若装置匀速转动的角速度为ω1时,细线AB上的张力为零而细线AC与竖直方向夹角仍为37°,求角速度ω1的大小;
(2)若装置匀速转动的角速度ω2= rad/s,求细线AC与竖直方向的夹角;
(3)装置可以以不同的角速度匀速转动,试通过计算讨论细线AC上张力T随ω2的变化关系(请用m、l和ω表示)。
1.【解析】选B。根据T=可知,周期与角速度成反比,故A项错误;角速度是描述匀速圆周运动速度方向变化快慢的物理量,线速度表示单位时间内转过的弧长,都可以描述运动的快慢,故B正确;匀速圆周运动的过程中,线速度的大小不变,但方向改变,所以线速度改变,故C项错误;向心加速度方向始终指向圆心,是个变量,故D项错误。
2.【解析】选B。根据角速度和周期的关系可知,周期T=,故A项错误;线速度大小v=ωR,故B项正确;座舱做匀速圆周运动,受到的合外力充当向心力,故合力大小F=mω2R,由于座舱所受合外力为重力与摩天轮对座舱的作用力的合力,故摩天轮对座舱的作用力不等于mg,也不等于mω2R,故C、D错误。
3.【解析】选C。A、B为皮带传动,所以线速度相等,则由向心加速度公式an=,又因A的半径大于B的半径,可知,A的向心加速度小于B的向心加速度,故A项错误;B与C绕同一转轴转动,角速度相等,根据an=ω2r可知半径大的向心加速度大,则C的向心加速度大,故B项错误;由以上分析可知,C点的向心加速度最大,故C项正确,D项错误。
4.【解析】选A。四辆小“自行车”属于同轴转动,所以“自行车”上的每个小孩的角速度相同,A正确;线速度是矢量,各个小孩的线速度方向不同,所以线速度不同,B错误;向心加速度指向圆心,所以每个小孩的向心加速度方向不同,C错误;由于每个小孩的质量可能不同,所以其所需的向心力大小可能不同,D错误。
5.【解析】选A。ωc=2ωa、ωc=ωd,则ωd=2ωa;又ra=2r、rd=4r;据a=rω2可得,ad=8aa,故A错误;小轮与右轮间靠摩擦传动不打滑,两轮边缘上点的线速度大小相等,即va=vc,故B正确;va=vc、ra=2r、rc=r,据ω=可得,ωc=2ωa;a、b两点均在右轮上,ωa=ωb;所以ωc=2ωb,故C正确;大轮与小轮同轴转动,则ωc=ωd;又ωc=2ωb,所以ωd=2ωb。据T=可得,Tb=2Td,故D正确。
6.【解析】选C。大齿轮带动小齿轮转动,轮子边缘上的点在相同时间内走过的弧长相同,则线速度大小相等,即v1= v2,根据ω=知,r1>r2,则ω1<ω2,故C项正确。
7.【解析】选D。对座椅进行受力分析,如图
座椅所受重力和拉力的合力提供向心力,
mgtanθ=m(lsinθ+r)
解得l=-,
则要使夹角变大,可减小周期,或使钢丝绳的长度变长,或增大角速度,与座椅的质量无关,故D项正确,A、B、C错误。
8【解析】选D。三个物体都做匀速圆周运动,角速度相等,向心加速度an=ω2r,可见,半径越大,向心加速度越大,所以物体C的向心加速度最大,A正确;三个物体的合力都指向圆心,对任意一个受力分析,如图
支持力与重力平衡,由静摩擦力f提供向心力,则得
f=Fn。
根据题意,rC=2rA=2rB=2R
由向心力公式Fn=mω2r,
得三个物体所受的静摩擦力分别为:fA=(2m)ω2R=2mω2R,fB=mω2R。
fC=mω2(2R)=2mω2R,
故物体B受到的静摩擦力最小,B正确;当ω变大时,所需要的向心力也变大,当达到最大静摩擦力时,物体开始滑动。当转速增加时,A、C所需向心力同步增加,且保持相等。B所需向心力也增加,A和C所需的向心力与B所需的向心力保持2∶1的关系。由于B和C受到的最大静摩擦力始终相等,都比A小,所以C先滑动,A和B后同时滑动,C正确,D错误,本题选错误的,故选D。
9.【解析】选C。设小桶转到最高点时水恰好不从桶里流出来时,小桶的角速度为ω,则由牛顿第二定律得mg=mω2R,当mω2R>mg时,桶对水有向下的作用力,此时水不会洒出来,故C项正确。
10.【解析】选A。相同速率下汽车在最低点受到的支持力最大,即此时的最大速度就是全程允许的最大速率,根据FN1-mg=m,即v==10 m/s。由于v<=10 m/s,故在凸形桥最高点上汽车不会脱离桥面,所以汽车允许的最大速率为10 m/s,故A项正确。
11.【解析】选A。物体恰好不被抛出的临界条件是最高点重力恰好提供向心力,根据牛顿第二定律,有:mg=m,根据线速度定义公式有:v=2πrn,联立解得:n=,故A项正确。
12.【解析】选B。由题意知,缆车突然停车的瞬间,重物开始做圆周运动,其所受合力提供向心力,即:F-mg=m,其中F=2mg,解得:v=,故B项正确。
13.【解析】选C。球B运动到最高点时,杆对球B恰好无作用力,即重力恰好提供向心力,有mg=m,解得v=,故A错误;由于A、B两球的角速度相等,则球A的速度大小v′=,故B错误;球B到最高点时,对杆无弹力,此时球A受重力和拉力的合力提供向心力,有F-mg=m,解得:F=1.5mg,故C正确,D错误。
14.【解析】(1)在研究向心力的大小Fn与质量m、角速度ω和半径r之间的关系时,需先控制某些量不变,研究另外两个物理量的关系,该方法为控制变量法。
(2)由图可知图中两球受到的向心力相等,转动的半径相同,由于铝的密度小,则相同大小的铝球的质量小,由向心力的公式:Fn=mω2r,则ωA<ωB。
(3)选C。在质量和半径一定的情况下,向心力的大小与角速度平方成正比,故A项错误;图示的装置不能显示线速度的大小,故B项错误;在半径和角速度一定的情况下,向心力的大小与质量成正比,故C项正确;在质量和角速度一定的情况下,向心力的大小与半径成正比,故D项错误。
答案:(1)控制变量法 (2)< (3)C
15.【解析】(1)根据向心力公式:Fn=m ,而v= ,T=
得:Fn=mr。
(2)如图由几何关系可得:Fn=mgtanθ=mg。
(3)由上面分析得:mg=mr,整理得:=·h ,斜率表达式为:。
答案:(1)mr (2)mg (3)
16.【解析】(1)当恰由最大静摩擦力提供向心力时,绳子拉力为零且角速度达到最大,设转盘转动的角速度为ω0,则由μmg=mr (2分)
得ω0=。 (2分)
(2)当ω=时,ω>ω0,所以绳子的拉力F和最大静摩擦力共同提供向心力,此时,
F+μmg=mω2r (2分)
代入数据得F=μmg。 (2分)
答案:(1) (2)μmg
17.【解析】两个小球离开轨道后均做平抛运动,竖直方向上运动情况相同。
根据2R=gt2,可得t=2 (1分)
在最高点时,两小球受重力和管壁的作用力,这两个力的合力作为向心力,
对A球:3mg+mg=m (1分)
解得:vA=2, (1分)
则sA= vAt=4R (1分)
对B球:mg-0.75mg=m (2分)
解得:vB=, (1分)
则sB= vBt=R (1分)
A、B两球落地点间的距离等于它们平抛运动的水平位移之差,
则有:sA-sB=3R (1分)
即A、B两球落地点间的距离为3R。
答案:3R
18.【解析】选A。小球所受重力和杆的作用力的合力提供向心力,根据牛顿第二定律有:mgsinθ=mω2L,解得:sinθ=,故A项正确。
19.【解析】选D。根据题目条件无法确定A的质量和B的质量的大小,故A项错误;以A为研究对象,假设不受摩擦力,A受到重力和支持力,合力提供向心力,设此时对应的角速度为ωA,根据牛顿第二定律可得mAgtanα=mArA,其中rA=Rsinα,则ωA=,同理可得当B的摩擦力为零时,角速度为:ωB=;由于α>β,故A、B受到的摩擦力不可能同时为零,故B项错误;若A不受摩擦力,整体转动的角速度为:ωA=>ωB=,则B有向上的运动趋势,故B受沿容器壁向下的摩擦力,故C项错误;若转动的角速度ω>ωA,A和B受沿容器壁向下的摩擦力,如果角速度增大,则A、B受到的摩擦力都增大,故D项正确。
20.【解析】选B、C、D。小球从B到C的运动时间为t=0.3 s,那么,小球在C点的竖直分速度为:vy=gt=3 m/s。由小球恰好垂直与倾角为45°的斜面相碰可知水平分速度为:v==3 m/s,故小球在斜面上的相碰点C与B点的水平距离为:s=vt=0.9 m,故B项正确,A项错误;对小球在B点应用牛顿第二定律可得:FN+mg=m=9 N,所以,FN=-1 N,即管道对小球的支持力为1 N,方向竖直向上;由牛顿第三定律可得:小球经过管道的B点时,小球对管道的作用力大小为1 N,方向竖直向下,故C、D项正确。
21.?【解析】(1)从小球第1次到第n次通过A位置,
转动圈数为n-1,时间为t,故周期为:T=,故A错误;小球的线速度大小为:v==,故B正确;小球受重力和拉力,合力提供向心力,设绳与竖直方向的夹角为α,则:Tcosα=mg
Tsinα=F向
故F向=mgtanα=mg,故C错误;
若电动机的转速增加,则转动半径增加,故激光笔1、2应分别左移、上移,故D正确;故选B、D。
(2)小球做圆周运动的周期
T== s=2.00 s;
向心力:F向=mg=mR
解得:g==9.86 m/s2
答案:(1)B、D (2)2.00 9.86
22【解析】(1)细线AB上张力恰为零时有
mgtan37°=mlsin37°, (2分)
解得ω1== rad/s。 (1分)
(2)当ω2>ω1时, 细线AB应松弛,即
mgtanθ′=mlsinθ′, (2分)
解得cosθ′=,θ′=53°。
此时细线AB恰好竖直,但张力为零。 (1分)
(3)当ω<ω1时,细线AB水平,细线AC上张力的竖直分量等于小球的重力:
Tcosθ=mg, (2分)
解得T==12.5 N; (1分)
当ω1<ω<ω2时,细线AB松弛,细线AC上张力的水平分量等于小球做圆周运动需要的向心力
Tsinθ′=mω2lsinθ′, (1分)
T=mω2l。 (1分)
当ω>ω2时,细线AB在竖直方向绷直,仍然由细线AC上张力的水平分量提供小球做圆周运动需要的向心力Tsinθ′=mω2lsinθ′, (1分)
T=mω2l。 (1分)
综上所述:当ω<ω1时,T=12.5 N不变;
当ω>ω1时,T=mω2l。
答案:(1) rad/s (2)53°
(3)当ω<ω1时,T=12.5 N不变;当ω>ω1时,T=mω2l
- 1 -
