初中数学冀教版八年级下册21.4一次函数的应用练习题(Word版 含解析)
文档属性
| 名称 | 初中数学冀教版八年级下册21.4一次函数的应用练习题(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 147.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 11:11:03 | ||
图片预览



文档简介
初中数学冀教版八年级下册第二十一章21.4一次函数的应用练习题
一、选择题
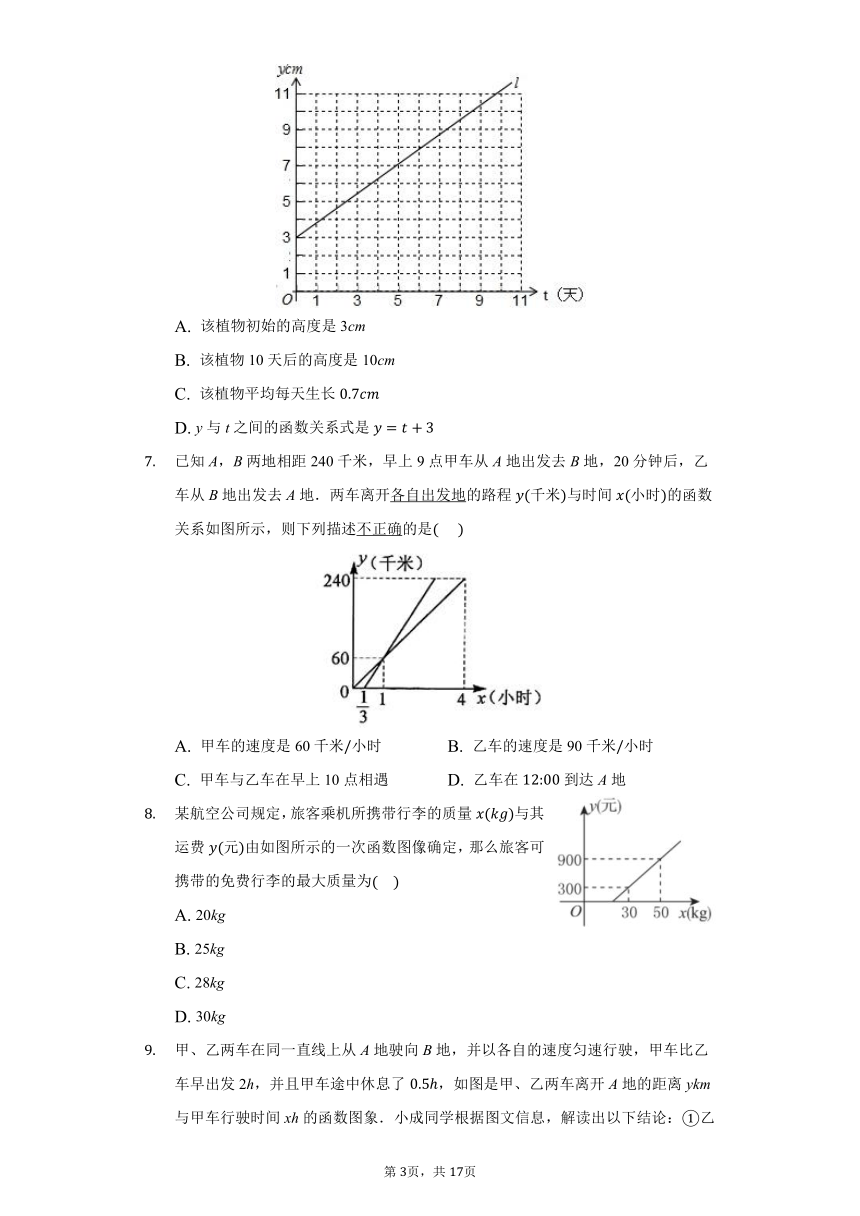
甲、乙两地高速铁路建设成功,一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为小时,两车之间的距离为千米,图中的折线表示y与x之间的函数关系,下列说法:
甲、乙两地相距1800千米;
点B的实际意义是两车出发后4小时相遇;
,;
动车的速度是450千米小时.
其中不正确的是
A.
B.
C.
D.
全民健身的今天,散步是大众喜欢的运动甲、乙两人在绿道上同时从同一起点以各自的速度匀速同向而行,步行一段时间后,甲因有事按原速度原路返回,此时乙仍按原速度继续前行甲乙两人之间的距离米与他们出发后的时间分的函数关系如图所示,已知甲步行速度比乙快由图象可知,甲、乙的速度分别是
A.
60米分,40米分
B.
80米分,60米分
C.
80米分,40米分
D.
120米分,80米分
甲、乙两人分别从A、B两地出发相向而行,和分别表示甲、乙两人离B地的距离与行走时间之间的关系,设甲、乙行走的速度分别是和,则
A.
B.
C.
D.
某快递公司甲、乙两名快递员7月上旬10天里派送快递,乙比甲晚工作一段时间,工作期间甲快递员因事停工3天,各自的工作效率一定,他们各自的工作量件随工作时间天变化的图象如图所示则有下列说法:甲工人的工作效率为60件天;乙工人每天比甲工人少送10件;甲工人一共送420件;乙比甲少工作2天其中正确的个数是
A.
1个
B.
2个
C.
3个
D.
4个
如图,设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车原地返回设x小时后两车间的距离为y千米,y关于x的函数关系如图所示,则乙车的速度为
A.
50千米小时
B.
45千米小时
C.
40千米小时
D.
35千米小时
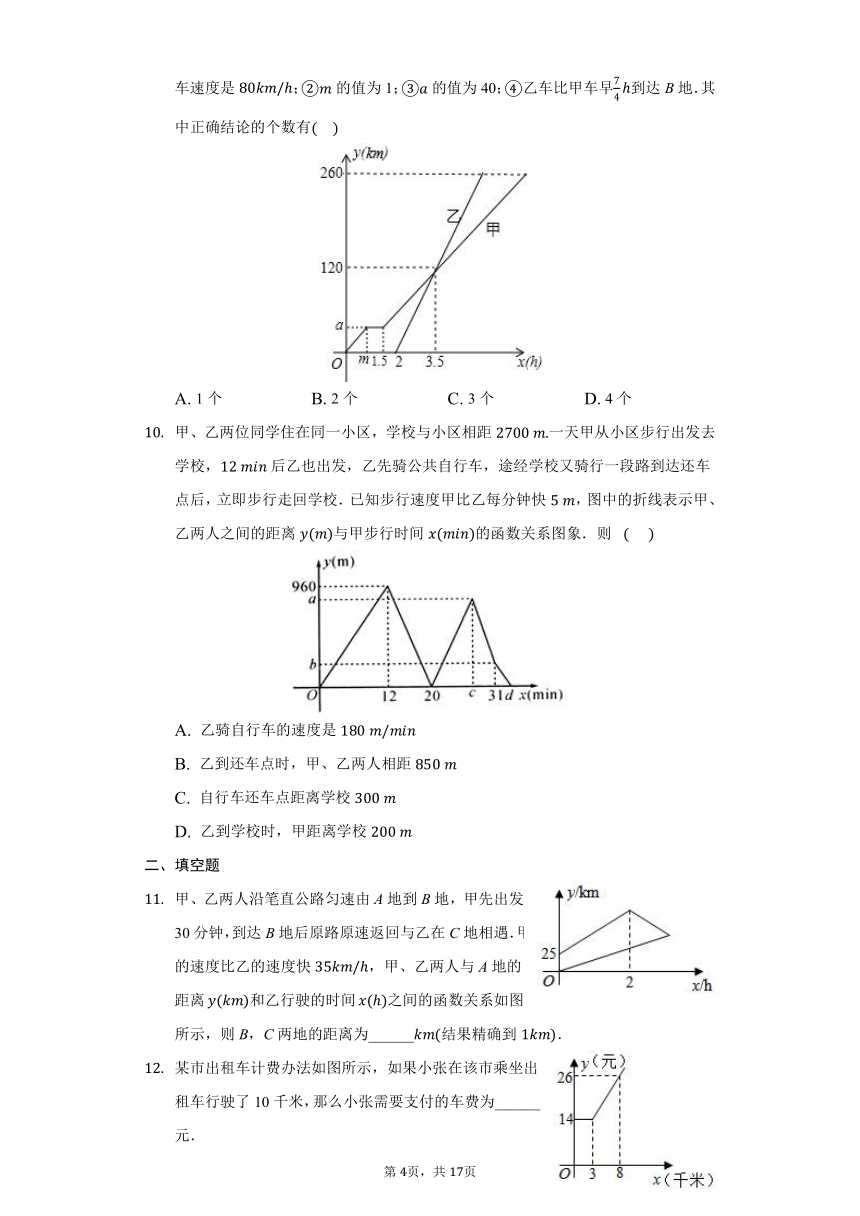
图象l表示的是某植物生长t天后的高度单位:与t之间的关系,根据图象,下列结论不正确的是
A.
该植物初始的高度是3cm
B.
该植物10天后的高度是10cm
C.
该植物平均每天生长
D.
y与t之间的函数关系式是
已知A,B两地相距240千米,早上9点甲车从A地出发去B地,20分钟后,乙车从B地出发去A地.两车离开各自出发地的路程千米与时间小时的函数关系如图所示,则下列描述不正确的是???
A.
甲车的速度是60千米小时
B.
乙车的速度是90千米小时
C.
甲车与乙车在早上10点相遇
D.
乙车在到达A地
某航空公司规定,旅客乘机所携带行李的质量与其运费元由如图所示的一次函数图像确定,那么旅客可携带的免费行李的最大质量为
A.
20kg
B.
25kg
C.
28kg
D.
30kg
甲、乙两车在同一直线上从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早出发2h,并且甲车途中休息了,如图是甲、乙两车离开A地的距离ykm与甲车行驶时间xh的函数图象.小成同学根据图文信息,解读出以下结论:乙车速度是;的值为1;的值为40;乙车比甲车早到达B地.其中正确结论的个数有??????
A.
1个
B.
2个
C.
3个
D.
4个
甲、乙两位同学住在同一小区,学校与小区相距一天甲从小区步行出发去学校,后乙也出发,乙先骑公共自行车,途经学校又骑行一段路到达还车点后,立即步行走回学校.已知步行速度甲比乙每分钟快,图中的折线表示甲、乙两人之间的距离与甲步行时间的函数关系图象.则?
???
A.
乙骑自行车的速度是
B.
乙到还车点时,甲、乙两人相距
C.
自行车还车点距离学校
D.
乙到学校时,甲距离学校
二、填空题
甲、乙两人沿笔直公路匀速由A地到B地,甲先出发30分钟,到达B地后原路原速返回与乙在C地相遇.甲的速度比乙的速度快,甲、乙两人与A地的距离和乙行驶的时间之间的函数关系如图所示,则B,C两地的距离为______结果精确到.
某市出租车计费办法如图所示,如果小张在该市乘坐出租车行驶了10千米,那么小张需要支付的车费为______元.
某高速列车公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费元是行李质量的一次函数,已知行李质量为30kg时,需付行李费4元;行李质量为40kg时,需付行李费12元,则旅客最多可免费携带______
kg行李.
某个周末,李海和他的叔叔先后从家出发,他们沿着同一条公路匀速前往某景区,李海8点骑着电动车出发,如图是他行驶路程随行驶时间变化的图象李海的叔叔开车9点出发,若要在10点至11点之间含10点和11点追上李海,则叔叔的开车速度的范围是______
.
三、解答题
某商场计划购进两种新型节能台灯共100盏,这两种台灯的进价、售价如下表所示:
类型
价格
进价元盏
售价元盖
A型
30
45
B型
50
70
若商场预计进货款为3500元,则这两种台灯各购进多少盏?
若商场规定B型台灯的进货数量不超过A型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
某市自来水公司为限制单位用水,每月只给某单位计划内用水3000吨,计划内用水每吨收费元,超计划部分每吨按元收费.
某月该单位用水3200吨,水费是______元;若用水2800吨,水费是______元;
写出该单位水费元与每月用水量吨之间的函数关系式;
若某月该单位缴纳水费1540元,则该单位这个月的用水多少吨?
一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.两车行驶的时间为xh,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系,根据图象解决以下问题:
甲、乙两地的距离为______km;
慢车的速度为______,快车的速度为______;
求当x为多少时,两车之间的距离为500km,请通过计算求出x的值.
生态公园计划在园内的坡地上造一片有A、B两种树的混合林,需要购买这两种树苗3000棵。A种树苗单价20元棵,成活率,劳务费4元棵;B种树苗单价25元棵,成活率,劳务费5元棵,设购买A种树苗x棵,造这片林的总费用为y元。解答下列问题:
求出元与棵之间的函数关系式;
假设这批树苗种植后成活2914棵,则造这片林的总费用需多少元?
答案和解析
1.【答案】D
【解析】解:由图象可知,甲、乙两地相距1800千米,故说法正确;
点B的实际意义是两车出发后4小时相遇,故说法正确;
普通列车的速度为:,动车的速度为:,故说法错误;
,
,,
故说法正确;
故选:D.
根据题意和函数图象中的数据可以判断各个小题中的结论是否正确,从而可以解答本题.
本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
2.【答案】A
【解析】解:根据题意可知,甲每分钟比乙快:米,
设乙的速度为x米分,则甲的速度为米分,
根据题意得:,
解得,
米分,
即甲的速度为米分,乙的速度为40米分,
故选:A.
根据题意可知,步行10分钟后甲开始返回,此时两人之间的距离为200米,可得他们的速度差为米分,再经过2分钟后两人相遇,根据相遇问题列方程解答即可.
本题考查一次函数的应用,解答此类问题的关键是明确题意,利用数形结合的思想解答.
3.【答案】B
【解析】解:设A、B两地的距离为skm,
,
解得,,
则,
则,
故选:B.
根据题意和函数图象中的数据,可以得到和的关系,从而可以解答本题.
本题考查一次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
4.【答案】C
【解析】解:甲的工作效率为件天,故正确.
乙的工作效率为件天,,故正确.
甲一共送了件,故正确.
甲工作7天,乙工作了6天,乙比甲少工作1天,故错误.
故选:C.
理由图象信息,根据工作效率、工作时间、工作量等关系一一解决问题即可.
本题考查一次函数的应用、工作量、工作时间、工作效率之间的关系等知识,解题的关键是读懂图象信息,属于中考常考题型.
5.【答案】B
【解析】解:设甲车的速度为,乙车的速度为,
由图象可知:,
解得:,
故选:B.
设甲车的速度为,乙车的速度为,根据题意列出方程即可求出答案.
本题考查一次函数的应用,解题的关键是正确找出题中的等量关系列出方程组,本题属于基础题型.
6.【答案】D
【解析】解:对于A,有图象中可知植物初始高度是3cm,故A选项正确,不符合题意;
对于B,图象中可知植物10天后高度是10,故B选项正确,不符合题意;
对于C,由10天内生长可知,平均每天生长,故C选项正确,不符合题意;
对于D,设函数解析式为,将和代入
,解得.
.
故D选项错误,符合题意.
故选:D.
根据图象上和的实际意义即可判断A,B两选项正误;由和可知该植物10天生长了7cm,可以算出平均每天生长长度判断C正误;设函数解析式为,将和代入求出解析式判断D选项正误.
本题考查了一次函数的应用,解决本题的关键是利用待定系数法求出一次函数的解析式.
7.【答案】C
【解析】
【分析】
本题主要考查了一次函数的应用及图像,关键是通过图象获取信息先根据图象获取信息,利用速度、路程和时间的关系计算可得结果.
【解答】
解:通过图象可得甲车行驶了4个小时的路程是240千米,则速度是千米小时,故A说法正确;
乙车行驶了小时的路程是60千米,则速度是千米小时,故B说法正确;
设乙车行驶x小时后相遇,根据题意可得,解得,
则甲车行驶时间为小时,即10点48分相遇,故C说法错误;
根据乙车的速度是90千米小时,路程是240千米可得所用时间为小时,小时,即3小时到达,则达到时间为点,故D说法正确,
故选C.
8.【答案】A
【解析】解:设y与x的函数关系式为,
由题意可知,所以,,所以函数关系式为,
当时,即,所以.
故选:A.
根据图中数据,用待定系数法求出直线解析式,然后求时,x对应的值即可.
本题重点考查了一次函数的图象及一次函数的应用,是一道难度中等的题目.
9.【答案】D
【解析】解:千米小时,
即乙车速度是,故正确;
由题意,得故正确;
,则,
故正确;
设甲车休息之后行驶路程与时间的函数关系式为,由题意,
得,解得,
,
根据图形得知:甲、乙两车中先到达B地的是乙车,
把代入得,,
乙车的行驶速度:,
乙车的行驶260km需要,
,
乙车比甲车早到达B地.故正确.
综上所述,正确结论的有共4个.
故选:D.
先由函数图象中的信息求出m的值,再根据“路程时间速度”求出甲的速度,并求出a的值;先根据图形判断甲、乙两车中先到达B地的是乙车,再把代入求得甲车到达B地的时间,再求出乙车行驶260km需要,即可得到结论.
本题主要考查了一次函数的应用,解决问题的关键是从图形中获得必要的信息进行计算,运用待定系数法求一次函数的解析式.解答此类试题时,需要掌握建立函数模型的方法以及采用分段函数解决问题的思想.
10.【答案】C
【解析】
【分析】
本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.根据甲12分钟步行了960米可得甲步行的速度,根据乙骑自行车8分钟行驶的路程比甲多960米即可得出乙骑自行车的速度;根据乙骑自行车的速度和乙步行的速度求出求出c的值,进而求出乙到还车点时,甲、乙两人的距离;同时可以求出自行车还车点到学校的距离;根据乙在甲出发31分后到达学校,即可求出乙到学校时,甲到学校的距离.
【解答】
解:甲步行的速度为:米分,
乙骑自行车的速度为:米分,
故选项A错误;
乙步行的速度为:米分,
乙全程:,解得,
所以乙骑自行车的路程为:米,
所以自行车还车点距离学校为:米,
故选项C正确;
乙到还车点时,乙的路程为3000米,甲步行的路程为:米,
此时两人相距:米,
故选项B错误;
乙到学校时,甲的路程为:米,
此时甲离学校:米.
故选项D错误.
故选C.
11.【答案】73
【解析】解:由题意可知,甲行驶的速度为:,A、B两地之间的距离为:,
乙的速度为:,
,
即乙出发小时后与甲相遇,
所以B,C两地的距离为:.
故答案为:73.
根据题意结合图象可得甲行驶的速度以及A、B两地之间的距离,进而得出乙行驶的速度,然后求出两人相遇的时间,即可求出B,C两地的距离.
本题考查了一次函数的应用,解决本题的关键是根据图象获取相关信息,求出A、B两地之间的距离.
12.【答案】
【解析】解:由图象可知,出租车的起步价是14元,在3千米内只收起步价,
设超过3千米的函数解析式为,则,解得,
超过3千米时所需费用y与x之间的函数关系式是,
出租车行驶了10千米则元,
故答案为.
设超过3千米的函数解析式为,根据题意列出方程组,利用待定系数法求得解析式,然后把代入即可求得.
此题主要考查了一次函数的应用、学会待定系数法确定函数解析式,正确由图象得出正确信息是解题关键,属于中考常考题型,
13.【答案】25
【解析】解:设行李费元与行李质量的函数关系式为,
行李质量为30kg时,需付行李费4元;行李质量为40kg时,需付行李费12元,
,
解得,
即行李费元与行李质量的函数关系式为,
当时,,解得,
故答案为:25.
根据当行李的质量超过规定时,需付的行李费元是行李质量的一次函数,已知行李质量为30kg时,需付行李费4元;行李质量为40kg时,需付行李费12元,可以求得y与x的函数关系式,然后令求出相应的x的值,即可得到旅客最多可免费携带多少kg的行李.
本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质解答.
14.【答案】
【解析】解:由图象可得,
李海的速度为,
李海的叔叔开车9点出发,要在10点至11点之间含10点和11点追上李海,
,得,
,得,
叔叔的开车速度的范围是,
故答案为:.
根据题意和函数图象中的数据,可以计算出李海的骑车速度和叔叔的开车速度的范围,本题得以解决.
本题考查一次函数的应用、一元一次不等式的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
15.【答案】解:设商场应购进A型台灯x盏,则B型台灯为盏,
根据题意得,,
解得,
所以,,
答:应购进A型台灯75盏,B型台灯25盏;
设商场销售完这批台灯可获利y元,
则,
,
,
型台灯的进货数量不超过A型台灯数量的3倍,
,
,
,
时,y取得最大值,为元
答:商场购进A型台灯25盏,B型台灯75盏,销售完这批台灯时获利最多,此时利润为1875元.
【解析】本题考查的是一元一次方程的应用,一次函数的应用.
设商场应购进A型台灯x盏,表示出B型台灯为盏,然后根据进货款型台灯的进货款型台灯的进货款列出方程求解即可;
设商场销售完这批台灯可获利y元,根据获利等于两种台灯的获利总和列式整理,再求出x的取值范围,然后根据一次函数的增减性求出获利的最大值.
16.【答案】1660?
1400
【解析】解:某月该单位用水3200吨,水费是:元;
若用水2800吨,水费是:元.
因为缴纳水费1540元,所以用水量应超过3000吨,故令,设用水x吨.
???????????
即该月的用水量是3050吨.
根据3000吨以内,用水每吨收费元,超计划部分每吨按元收费,即可求解;
根据收费标准,分吨,和吨两种情况进行讨论,分两种情况写出解析式;
该单位缴纳水费1540元一定是超过3000元,根据超过3000吨的情况的水费标准即可得到一个关于用水量的方程,即可求解.
本题考查的是用一次函数解决实际问题,正确理解收费标准,列出函数解析式是关键,此类题是近年中考中的热点问题.
17.【答案】720?
80?
120
【解析】解:甲、乙两地的距离为720km,
故答案为:720;
设慢车的速度为,快车的速度为,
根据题意,得,解得,
故答案为80,120;
由题意,可知两车行驶的过程中有2次两车之间的距离为500km.
即相遇前:,
解得,
相遇后:点,
慢车行驶20km两车之间的距离为500km,
慢车行驶20km需要的时间是,
,
故或,两车之间的距离为500km.
根据题意结合图象即可得出结果.
由图象可知,两车同时出发.等量关系有两个:慢车的速度快车的速度,慢车的速度快车的速度,设慢车的速度为,快车的速度为,依此列出方程组,求解即可;
分相遇前相距500km和相遇后相遇500km两种情况求解即可.
本题考查了一次函数的应用,主要利用了路程、时间、速度三者之间的关系,要分相遇前与相遇后两种情况讨论,这也是本题容易出错的地方.
18.【答案】解:根据题意得:
即元与棵之间的函数关系式为
根据题意得:,解得.
当时,
所以造这片林的总费用需81600元.
【解析】略
第2页,共2页
第1页,共1页
一、选择题
甲、乙两地高速铁路建设成功,一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为小时,两车之间的距离为千米,图中的折线表示y与x之间的函数关系,下列说法:
甲、乙两地相距1800千米;
点B的实际意义是两车出发后4小时相遇;
,;
动车的速度是450千米小时.
其中不正确的是
A.
B.
C.
D.
全民健身的今天,散步是大众喜欢的运动甲、乙两人在绿道上同时从同一起点以各自的速度匀速同向而行,步行一段时间后,甲因有事按原速度原路返回,此时乙仍按原速度继续前行甲乙两人之间的距离米与他们出发后的时间分的函数关系如图所示,已知甲步行速度比乙快由图象可知,甲、乙的速度分别是
A.
60米分,40米分
B.
80米分,60米分
C.
80米分,40米分
D.
120米分,80米分
甲、乙两人分别从A、B两地出发相向而行,和分别表示甲、乙两人离B地的距离与行走时间之间的关系,设甲、乙行走的速度分别是和,则
A.
B.
C.
D.
某快递公司甲、乙两名快递员7月上旬10天里派送快递,乙比甲晚工作一段时间,工作期间甲快递员因事停工3天,各自的工作效率一定,他们各自的工作量件随工作时间天变化的图象如图所示则有下列说法:甲工人的工作效率为60件天;乙工人每天比甲工人少送10件;甲工人一共送420件;乙比甲少工作2天其中正确的个数是
A.
1个
B.
2个
C.
3个
D.
4个
如图,设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车原地返回设x小时后两车间的距离为y千米,y关于x的函数关系如图所示,则乙车的速度为
A.
50千米小时
B.
45千米小时
C.
40千米小时
D.
35千米小时
图象l表示的是某植物生长t天后的高度单位:与t之间的关系,根据图象,下列结论不正确的是
A.
该植物初始的高度是3cm
B.
该植物10天后的高度是10cm
C.
该植物平均每天生长
D.
y与t之间的函数关系式是
已知A,B两地相距240千米,早上9点甲车从A地出发去B地,20分钟后,乙车从B地出发去A地.两车离开各自出发地的路程千米与时间小时的函数关系如图所示,则下列描述不正确的是???
A.
甲车的速度是60千米小时
B.
乙车的速度是90千米小时
C.
甲车与乙车在早上10点相遇
D.
乙车在到达A地
某航空公司规定,旅客乘机所携带行李的质量与其运费元由如图所示的一次函数图像确定,那么旅客可携带的免费行李的最大质量为
A.
20kg
B.
25kg
C.
28kg
D.
30kg
甲、乙两车在同一直线上从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早出发2h,并且甲车途中休息了,如图是甲、乙两车离开A地的距离ykm与甲车行驶时间xh的函数图象.小成同学根据图文信息,解读出以下结论:乙车速度是;的值为1;的值为40;乙车比甲车早到达B地.其中正确结论的个数有??????
A.
1个
B.
2个
C.
3个
D.
4个
甲、乙两位同学住在同一小区,学校与小区相距一天甲从小区步行出发去学校,后乙也出发,乙先骑公共自行车,途经学校又骑行一段路到达还车点后,立即步行走回学校.已知步行速度甲比乙每分钟快,图中的折线表示甲、乙两人之间的距离与甲步行时间的函数关系图象.则?
???
A.
乙骑自行车的速度是
B.
乙到还车点时,甲、乙两人相距
C.
自行车还车点距离学校
D.
乙到学校时,甲距离学校
二、填空题
甲、乙两人沿笔直公路匀速由A地到B地,甲先出发30分钟,到达B地后原路原速返回与乙在C地相遇.甲的速度比乙的速度快,甲、乙两人与A地的距离和乙行驶的时间之间的函数关系如图所示,则B,C两地的距离为______结果精确到.
某市出租车计费办法如图所示,如果小张在该市乘坐出租车行驶了10千米,那么小张需要支付的车费为______元.
某高速列车公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费元是行李质量的一次函数,已知行李质量为30kg时,需付行李费4元;行李质量为40kg时,需付行李费12元,则旅客最多可免费携带______
kg行李.
某个周末,李海和他的叔叔先后从家出发,他们沿着同一条公路匀速前往某景区,李海8点骑着电动车出发,如图是他行驶路程随行驶时间变化的图象李海的叔叔开车9点出发,若要在10点至11点之间含10点和11点追上李海,则叔叔的开车速度的范围是______
.
三、解答题
某商场计划购进两种新型节能台灯共100盏,这两种台灯的进价、售价如下表所示:
类型
价格
进价元盏
售价元盖
A型
30
45
B型
50
70
若商场预计进货款为3500元,则这两种台灯各购进多少盏?
若商场规定B型台灯的进货数量不超过A型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
某市自来水公司为限制单位用水,每月只给某单位计划内用水3000吨,计划内用水每吨收费元,超计划部分每吨按元收费.
某月该单位用水3200吨,水费是______元;若用水2800吨,水费是______元;
写出该单位水费元与每月用水量吨之间的函数关系式;
若某月该单位缴纳水费1540元,则该单位这个月的用水多少吨?
一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.两车行驶的时间为xh,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系,根据图象解决以下问题:
甲、乙两地的距离为______km;
慢车的速度为______,快车的速度为______;
求当x为多少时,两车之间的距离为500km,请通过计算求出x的值.
生态公园计划在园内的坡地上造一片有A、B两种树的混合林,需要购买这两种树苗3000棵。A种树苗单价20元棵,成活率,劳务费4元棵;B种树苗单价25元棵,成活率,劳务费5元棵,设购买A种树苗x棵,造这片林的总费用为y元。解答下列问题:
求出元与棵之间的函数关系式;
假设这批树苗种植后成活2914棵,则造这片林的总费用需多少元?
答案和解析
1.【答案】D
【解析】解:由图象可知,甲、乙两地相距1800千米,故说法正确;
点B的实际意义是两车出发后4小时相遇,故说法正确;
普通列车的速度为:,动车的速度为:,故说法错误;
,
,,
故说法正确;
故选:D.
根据题意和函数图象中的数据可以判断各个小题中的结论是否正确,从而可以解答本题.
本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
2.【答案】A
【解析】解:根据题意可知,甲每分钟比乙快:米,
设乙的速度为x米分,则甲的速度为米分,
根据题意得:,
解得,
米分,
即甲的速度为米分,乙的速度为40米分,
故选:A.
根据题意可知,步行10分钟后甲开始返回,此时两人之间的距离为200米,可得他们的速度差为米分,再经过2分钟后两人相遇,根据相遇问题列方程解答即可.
本题考查一次函数的应用,解答此类问题的关键是明确题意,利用数形结合的思想解答.
3.【答案】B
【解析】解:设A、B两地的距离为skm,
,
解得,,
则,
则,
故选:B.
根据题意和函数图象中的数据,可以得到和的关系,从而可以解答本题.
本题考查一次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
4.【答案】C
【解析】解:甲的工作效率为件天,故正确.
乙的工作效率为件天,,故正确.
甲一共送了件,故正确.
甲工作7天,乙工作了6天,乙比甲少工作1天,故错误.
故选:C.
理由图象信息,根据工作效率、工作时间、工作量等关系一一解决问题即可.
本题考查一次函数的应用、工作量、工作时间、工作效率之间的关系等知识,解题的关键是读懂图象信息,属于中考常考题型.
5.【答案】B
【解析】解:设甲车的速度为,乙车的速度为,
由图象可知:,
解得:,
故选:B.
设甲车的速度为,乙车的速度为,根据题意列出方程即可求出答案.
本题考查一次函数的应用,解题的关键是正确找出题中的等量关系列出方程组,本题属于基础题型.
6.【答案】D
【解析】解:对于A,有图象中可知植物初始高度是3cm,故A选项正确,不符合题意;
对于B,图象中可知植物10天后高度是10,故B选项正确,不符合题意;
对于C,由10天内生长可知,平均每天生长,故C选项正确,不符合题意;
对于D,设函数解析式为,将和代入
,解得.
.
故D选项错误,符合题意.
故选:D.
根据图象上和的实际意义即可判断A,B两选项正误;由和可知该植物10天生长了7cm,可以算出平均每天生长长度判断C正误;设函数解析式为,将和代入求出解析式判断D选项正误.
本题考查了一次函数的应用,解决本题的关键是利用待定系数法求出一次函数的解析式.
7.【答案】C
【解析】
【分析】
本题主要考查了一次函数的应用及图像,关键是通过图象获取信息先根据图象获取信息,利用速度、路程和时间的关系计算可得结果.
【解答】
解:通过图象可得甲车行驶了4个小时的路程是240千米,则速度是千米小时,故A说法正确;
乙车行驶了小时的路程是60千米,则速度是千米小时,故B说法正确;
设乙车行驶x小时后相遇,根据题意可得,解得,
则甲车行驶时间为小时,即10点48分相遇,故C说法错误;
根据乙车的速度是90千米小时,路程是240千米可得所用时间为小时,小时,即3小时到达,则达到时间为点,故D说法正确,
故选C.
8.【答案】A
【解析】解:设y与x的函数关系式为,
由题意可知,所以,,所以函数关系式为,
当时,即,所以.
故选:A.
根据图中数据,用待定系数法求出直线解析式,然后求时,x对应的值即可.
本题重点考查了一次函数的图象及一次函数的应用,是一道难度中等的题目.
9.【答案】D
【解析】解:千米小时,
即乙车速度是,故正确;
由题意,得故正确;
,则,
故正确;
设甲车休息之后行驶路程与时间的函数关系式为,由题意,
得,解得,
,
根据图形得知:甲、乙两车中先到达B地的是乙车,
把代入得,,
乙车的行驶速度:,
乙车的行驶260km需要,
,
乙车比甲车早到达B地.故正确.
综上所述,正确结论的有共4个.
故选:D.
先由函数图象中的信息求出m的值,再根据“路程时间速度”求出甲的速度,并求出a的值;先根据图形判断甲、乙两车中先到达B地的是乙车,再把代入求得甲车到达B地的时间,再求出乙车行驶260km需要,即可得到结论.
本题主要考查了一次函数的应用,解决问题的关键是从图形中获得必要的信息进行计算,运用待定系数法求一次函数的解析式.解答此类试题时,需要掌握建立函数模型的方法以及采用分段函数解决问题的思想.
10.【答案】C
【解析】
【分析】
本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.根据甲12分钟步行了960米可得甲步行的速度,根据乙骑自行车8分钟行驶的路程比甲多960米即可得出乙骑自行车的速度;根据乙骑自行车的速度和乙步行的速度求出求出c的值,进而求出乙到还车点时,甲、乙两人的距离;同时可以求出自行车还车点到学校的距离;根据乙在甲出发31分后到达学校,即可求出乙到学校时,甲到学校的距离.
【解答】
解:甲步行的速度为:米分,
乙骑自行车的速度为:米分,
故选项A错误;
乙步行的速度为:米分,
乙全程:,解得,
所以乙骑自行车的路程为:米,
所以自行车还车点距离学校为:米,
故选项C正确;
乙到还车点时,乙的路程为3000米,甲步行的路程为:米,
此时两人相距:米,
故选项B错误;
乙到学校时,甲的路程为:米,
此时甲离学校:米.
故选项D错误.
故选C.
11.【答案】73
【解析】解:由题意可知,甲行驶的速度为:,A、B两地之间的距离为:,
乙的速度为:,
,
即乙出发小时后与甲相遇,
所以B,C两地的距离为:.
故答案为:73.
根据题意结合图象可得甲行驶的速度以及A、B两地之间的距离,进而得出乙行驶的速度,然后求出两人相遇的时间,即可求出B,C两地的距离.
本题考查了一次函数的应用,解决本题的关键是根据图象获取相关信息,求出A、B两地之间的距离.
12.【答案】
【解析】解:由图象可知,出租车的起步价是14元,在3千米内只收起步价,
设超过3千米的函数解析式为,则,解得,
超过3千米时所需费用y与x之间的函数关系式是,
出租车行驶了10千米则元,
故答案为.
设超过3千米的函数解析式为,根据题意列出方程组,利用待定系数法求得解析式,然后把代入即可求得.
此题主要考查了一次函数的应用、学会待定系数法确定函数解析式,正确由图象得出正确信息是解题关键,属于中考常考题型,
13.【答案】25
【解析】解:设行李费元与行李质量的函数关系式为,
行李质量为30kg时,需付行李费4元;行李质量为40kg时,需付行李费12元,
,
解得,
即行李费元与行李质量的函数关系式为,
当时,,解得,
故答案为:25.
根据当行李的质量超过规定时,需付的行李费元是行李质量的一次函数,已知行李质量为30kg时,需付行李费4元;行李质量为40kg时,需付行李费12元,可以求得y与x的函数关系式,然后令求出相应的x的值,即可得到旅客最多可免费携带多少kg的行李.
本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质解答.
14.【答案】
【解析】解:由图象可得,
李海的速度为,
李海的叔叔开车9点出发,要在10点至11点之间含10点和11点追上李海,
,得,
,得,
叔叔的开车速度的范围是,
故答案为:.
根据题意和函数图象中的数据,可以计算出李海的骑车速度和叔叔的开车速度的范围,本题得以解决.
本题考查一次函数的应用、一元一次不等式的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
15.【答案】解:设商场应购进A型台灯x盏,则B型台灯为盏,
根据题意得,,
解得,
所以,,
答:应购进A型台灯75盏,B型台灯25盏;
设商场销售完这批台灯可获利y元,
则,
,
,
型台灯的进货数量不超过A型台灯数量的3倍,
,
,
,
时,y取得最大值,为元
答:商场购进A型台灯25盏,B型台灯75盏,销售完这批台灯时获利最多,此时利润为1875元.
【解析】本题考查的是一元一次方程的应用,一次函数的应用.
设商场应购进A型台灯x盏,表示出B型台灯为盏,然后根据进货款型台灯的进货款型台灯的进货款列出方程求解即可;
设商场销售完这批台灯可获利y元,根据获利等于两种台灯的获利总和列式整理,再求出x的取值范围,然后根据一次函数的增减性求出获利的最大值.
16.【答案】1660?
1400
【解析】解:某月该单位用水3200吨,水费是:元;
若用水2800吨,水费是:元.
因为缴纳水费1540元,所以用水量应超过3000吨,故令,设用水x吨.
???????????
即该月的用水量是3050吨.
根据3000吨以内,用水每吨收费元,超计划部分每吨按元收费,即可求解;
根据收费标准,分吨,和吨两种情况进行讨论,分两种情况写出解析式;
该单位缴纳水费1540元一定是超过3000元,根据超过3000吨的情况的水费标准即可得到一个关于用水量的方程,即可求解.
本题考查的是用一次函数解决实际问题,正确理解收费标准,列出函数解析式是关键,此类题是近年中考中的热点问题.
17.【答案】720?
80?
120
【解析】解:甲、乙两地的距离为720km,
故答案为:720;
设慢车的速度为,快车的速度为,
根据题意,得,解得,
故答案为80,120;
由题意,可知两车行驶的过程中有2次两车之间的距离为500km.
即相遇前:,
解得,
相遇后:点,
慢车行驶20km两车之间的距离为500km,
慢车行驶20km需要的时间是,
,
故或,两车之间的距离为500km.
根据题意结合图象即可得出结果.
由图象可知,两车同时出发.等量关系有两个:慢车的速度快车的速度,慢车的速度快车的速度,设慢车的速度为,快车的速度为,依此列出方程组,求解即可;
分相遇前相距500km和相遇后相遇500km两种情况求解即可.
本题考查了一次函数的应用,主要利用了路程、时间、速度三者之间的关系,要分相遇前与相遇后两种情况讨论,这也是本题容易出错的地方.
18.【答案】解:根据题意得:
即元与棵之间的函数关系式为
根据题意得:,解得.
当时,
所以造这片林的总费用需81600元.
【解析】略
第2页,共2页
第1页,共1页
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
