2020——2021学年人教版 九年级数学下册 第二十七章 相似 章末训练(word含答案)
文档属性
| 名称 | 2020——2021学年人教版 九年级数学下册 第二十七章 相似 章末训练(word含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 588.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 11:04:42 | ||
图片预览




文档简介
人教版 九年级数学下册 第二十七章 相似 章末训练
一、选择题
1. (2020·内江)如图,在中,D、E分别是AB和AC的中点,,则( )
A. 30 B. 25 C. 22.5 D. 20
2. (2020·嘉兴) 如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的位似比为的位似图形△OCD,则点C坐标为( )
A.(﹣1,﹣1) B.() C.() D.(﹣2,﹣1)
3. (2019?重庆)下列命题是真命题的是
A.如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为2∶3
B.如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为4∶9
C.如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为2∶3
D.如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为4∶9
4. (2020·云南)如图,平行四边形ABCD的对角线AC,BD相交于点O,E是CD的中点.则△DEO与△BCD的面积的比等于( )
A. B. C. D.
5. (2020·营口)如图,在△ABC中,DE∥AB,且=,则的值为( )
A. B. C. D.
6. (2019?巴中)如图ABCD,F为BC中点,延长AD至E,使,连接EF交DC于点G,则=
A.2∶3 B.3∶2
C.9∶4 D.4∶9
7. (2019?贵港)如图,在中,点,分别在,边上,,,若,,则线段的长为
A. B.
C. D.5
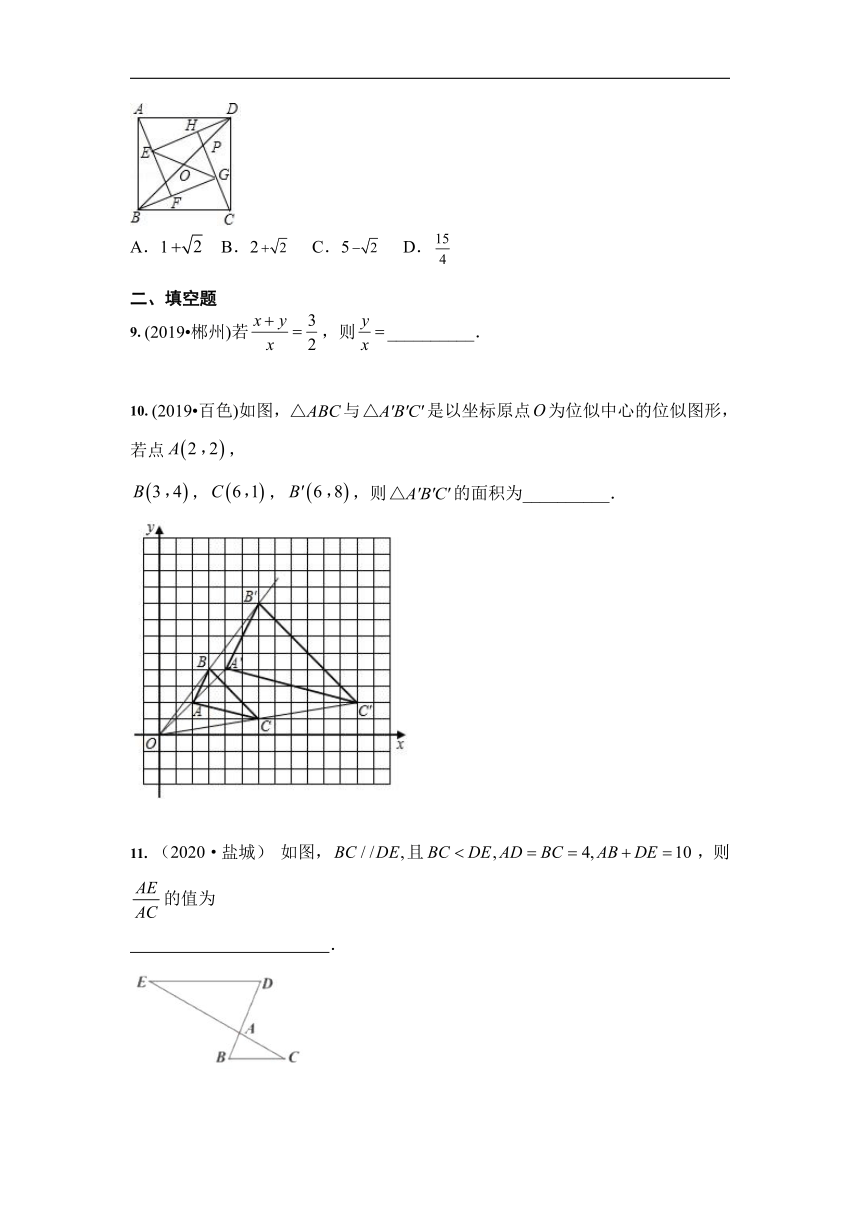
8. (2020?丽水)如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH.连结EG,BD相交于点O、BD与HC相交于点P.若GO=GP,则的值是( )
A.1 B.2 C.5 D.
二、填空题
9. (2019?郴州)若,则__________.
10. (2019?百色)如图,与是以坐标原点为位似中心的位似图形,若点,
,,,则的面积为__________.
11. (2020·盐城) 如图,且,则的值为
.
12. (2020·吉林)如图,在中,,分别是边,的中点.若的面积为.则四边形的面积为_______.
13. (2019?永州)如图,已知点F是△ABC的重心,连接BF并延长,交AC于点E,连接CF并延长,交AB于点D,过点F作FG∥BC,交AC于点G.设三角形EFG,四边形FBCG的面积分别为S1,S2,则S1:S2=__________.
14. 在平面直角坐标系中,点A关于y轴的对称点为点B,点A关于原点O的对称点为点C.
(1)若点A的坐标为(1,2),请你在给出的坐标系中画出△ABC.设AB与y轴的交点为D,则=__________;
(2)若点A的坐标为(a,b)(ab≠0),则△ABC的形状为____________.
15. (2020·东营)如图,P为平行四边形ABCD边BC边上一点,E、F分别为PA、PD上的点,且PA=3PE,PD=3PF,△PEF、△PDC、△PAB的面积分别记为、、,若=2,则+= .
16. (2019?泸州)如图,在等腰中,,,点在边上,,点在边上,,垂足为,则长为__________.
三、解答题
17. (2020·杭州)如图,在中,点D,E,F分别在AB,BC,AC边上,,.
(1)求证:.
(2)设,
①若BC=12,求线段BE的长;
②若△EFC的面积是20,求△ABC的面积.
18. 如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC、CD于点P、Q.
(1)请写出图中各对相似三角形(相似比为1除外);
(2)求BP∶PQ∶QR.
19. (2020·攀枝花)三角形三条边上的中线交于一点,这个点叫三角形的重心.如图是的重心.求证:.
20. (2020·南京)如图,在△ABC和△A’B’C’中,D、D’分别是AB、A’B’上一点,=.
(1)当==时,求证:△ABC∽△A’B’C’.
证明的途径可以用下面的框图表示,请填写其中的空格.
(2)当==时,判断△ABC与△A’B’C’是否相似,并说明理由.
人教版 九年级数学下册 第二十七章 相似 章末训练-答案
一、选择题
1. 【答案】 D
【解析】本题考查了相似三角形的判定与性质,解答本题的关键是得出DE是中位线,从而判断△ADE∽△ABC,然后掌握相似三角形的面积比等于相似比的平方即可求解本题.首先判断出△ADE∽△ABC,然后根据相似三角形的面积比等于相似比的平方即可求出△ABC的面积.
根据题意,点D和点E分别是AB和AC的中点,则DE∥BC且DE=BC,故可以判断出△ADE∽△ABC,根据相似三角形的面积比等于相似比的平方,可知:=1:4,则:=3:4,题中已知,故可得=5,=20,因此本题选D.
2. 【答案】B
【解析】本题考查了在坐标系中,位似图形点的坐标.在平面直角坐标系中,如果以原点为位似中心,画出一个与原图形位似的图形,使它与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(–kx,–ky).由A(4,3),位似比k=,可得C()因此本题选B.
3. 【答案】B
【解析】A、如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为4∶9,是假命题;
B、如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为4∶9,是真命题;
C、如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为16∶81,是假命题;
D、如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为16∶81,是假命题,
故选B.
4. 【答案】 B.
【解析】利用平行四边形的性质可得出点O为线段BD的中点,结合点E是CD的中点可得出线段OE为△DBC的中位线,利用三角形中位线定理可得出OE∥BC,OE=BC,进而可得出△DOE∽△DBC,再利用相似三角形的面积比等于相似比的平分,即可求出△DEO与△BCD的面积的比为1:4.
5. 【答案】A
【解析】利用平行截割定理求的值.∵DE∥AB,∴==,∵CE+AE=AC,∴=.
6. 【答案】D
【解析】设,∵,∴,
∵四边形ABCD是平行四边形,∴,,
∵点F是BC的中点,∴,
∵,∴,
∴,故选D.
7. 【答案】C
【解析】设,,∴,
∵,∴,
∴,∴,
∴,,
∵,,∴,
∵,∴,
∴,
设,,∴,
∴,∴,∴,
故选C.
8. 【答案】C
【解析】∵四边形EFGH为正方形,∴∠EGH=45°,∠FGH=90°,∵OG=GP,∴∠GOP=∠OPG=67.5°,∴∠PBG=22.5°,又∵∠DBC=45°,∴∠GBC=22.5°,∴∠PBG=∠GBC,
∵∠BGP=∠BG=90°,BG=BG,∴△BPG≌△BCG,∴PG=CG.设OG=PG=CG=x,
∵O为EG,BD的交点,∴EG=2x,FGx.∵四个全等的直角三角形拼成“赵爽弦图”,∴BF=CG=x,
∴BG=xx,∴BC2=BG2+CG2,
∴,因此本题选D.
二、填空题
9. 【答案】
【解析】∵,∴,
故2y=x,则,故答案为:.
10. 【答案】18
【解析】∵与是以坐标原点为位似中心的位似图形,
若点,,∴位似比为,
∵,,
∴,
∴的面积为:,
故答案为:18.
11. 【答案】2
【解析】∵BC∥DE,∴△ADE∽△ABC,∴ ,设DE=x,则AB=10-x∵AD=BC=4,∴,∴x1=8 ,x2=2(舍去), ,此本题答案为2 .
12. 【答案】
【解析】点,分别是边,的中点,
,即
又,
则四边形的面积为.
故答案为:.
13. 【答案】
【解析】∵点F是△ABC的重心,∴BF=2EF,∴BE=3EF,
∵FG∥BC,∴△EFG∽△EBC,
∴,()2,
∴S1∶S2,故答案为:.
14. 【答案】(1)△ABC如图 (2)直角三角形 解析:(1)因为点A的坐标为(1,2),所以点A关于y轴的对称点B的坐标为(-1,2),关于原点的对称点C的坐标为(-1,-2).连AB,BC,AC,作△ABC.
设AB交y轴于D点,如图,
D点坐标为(0,2),
∵OD∥BC,
∴△ADO∽△ABC.
∴==.
(2)∵ab≠0,∴a≠0,且b≠0,
∴点A不在坐标轴上,
∴AB∥x轴,BC⊥x轴.
∴∠ABC=90°.
∴△ABC是直角三角形.
15. 【答案】18
【解析】本题考查了相似三角形的判定、性质,三角形的面积,解题的关键是根据已知条件推出相似三角形,并由相似比得到面积比.
∵PA=3PE,PD=3PF,∠APD =∠EPF,∴△PEF∽△PAD,相似比为1︰3,
∵△PEF的面积为=2,∴=9S=9×2=18,
∴+==18.
16. 【答案】
【解析】如图,过作于,则∠AHD=90°,
∵在等腰中,,,
∴,,
∴∠ADH=90°–∠CAD=45°=∠CAD,
∴,
∴CH=AC–AH=15–DH,
∵,∴,
又∵∠ANH=∠DNF,∴,
∴,∴,
∵,CE+BE=BC=15,∴,
∴,
∴,
∴,故答案为:.
三、解答题
17. 【答案】
解: (1)∵DE∥AC,∴∠BED=∠C.∵EF∥AB,∴∠B=∠FEC,∴△BDE∽△EFC.
(2)①∵EF∥AB,∴==.∵BC=12,∴=,∴BE=4.
②∵EF∥AB,∴△EFC△BAC,∴=.∵=,∴=.又∵△EFC的面积是20,∴=,∴S△ABC=45,即△ABC的面积是45.
18. 【答案】
解:(1)△BCP∽△BER,△PCQ∽△PAB,△PCQ∽△RDQ,△PAB∽△RDQ.
(2)∵四边形ABCD和四边形ACED都是平行四边形,
∴BC=AD=CE,AC∥DE,∴PB=PR,=.
又∵PC∥DR,∴△PCQ∽△RDQ.
∵点R是DE的中点,∴DR=RE.
∴===,∴QR=2PQ.
又∵BP=PR=PQ+QR=3PQ,
∴BP∶PQ∶QR=3∶1∶2.
19. 【答案】
证明:连接DE,
∵点G是△ABC的重心,
∴点E和点D分别是AB和BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC且DE=AC,
∴△DEG∽△ACG,
∴,
∴
∴AD=3DG,
即AD=3GD.
20. 【答案】
解:(1) == ∠A=∠A’.
(2)如图,过点D、D’分别作DE∥BC,D’E’∥B’C’,DE交AC于点E,D’E’交A’C’于点E’.
∵DE∥BC,
∴△ADE∽△ABC.
∴==.
同理==.
又=,
∴=,
∴=.
同理 =.
∴=,即=.
∴=.
又==,
∴==,
∴△DCE∽△D’C’E’.
∴∠CED=∠C’E’D’.
∵DE∥BC,
∴∠CED+∠ACB=180°.
同理 ∠C’E’D’+∠A’C’B’=180°.
∴∠ACB=∠A’C’B’.
又=
∴△ABC∽△A’B’C’.
一、选择题
1. (2020·内江)如图,在中,D、E分别是AB和AC的中点,,则( )
A. 30 B. 25 C. 22.5 D. 20
2. (2020·嘉兴) 如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的位似比为的位似图形△OCD,则点C坐标为( )
A.(﹣1,﹣1) B.() C.() D.(﹣2,﹣1)
3. (2019?重庆)下列命题是真命题的是
A.如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为2∶3
B.如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为4∶9
C.如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为2∶3
D.如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为4∶9
4. (2020·云南)如图,平行四边形ABCD的对角线AC,BD相交于点O,E是CD的中点.则△DEO与△BCD的面积的比等于( )
A. B. C. D.
5. (2020·营口)如图,在△ABC中,DE∥AB,且=,则的值为( )
A. B. C. D.
6. (2019?巴中)如图ABCD,F为BC中点,延长AD至E,使,连接EF交DC于点G,则=
A.2∶3 B.3∶2
C.9∶4 D.4∶9
7. (2019?贵港)如图,在中,点,分别在,边上,,,若,,则线段的长为
A. B.
C. D.5
8. (2020?丽水)如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH.连结EG,BD相交于点O、BD与HC相交于点P.若GO=GP,则的值是( )
A.1 B.2 C.5 D.
二、填空题
9. (2019?郴州)若,则__________.
10. (2019?百色)如图,与是以坐标原点为位似中心的位似图形,若点,
,,,则的面积为__________.
11. (2020·盐城) 如图,且,则的值为
.
12. (2020·吉林)如图,在中,,分别是边,的中点.若的面积为.则四边形的面积为_______.
13. (2019?永州)如图,已知点F是△ABC的重心,连接BF并延长,交AC于点E,连接CF并延长,交AB于点D,过点F作FG∥BC,交AC于点G.设三角形EFG,四边形FBCG的面积分别为S1,S2,则S1:S2=__________.
14. 在平面直角坐标系中,点A关于y轴的对称点为点B,点A关于原点O的对称点为点C.
(1)若点A的坐标为(1,2),请你在给出的坐标系中画出△ABC.设AB与y轴的交点为D,则=__________;
(2)若点A的坐标为(a,b)(ab≠0),则△ABC的形状为____________.
15. (2020·东营)如图,P为平行四边形ABCD边BC边上一点,E、F分别为PA、PD上的点,且PA=3PE,PD=3PF,△PEF、△PDC、△PAB的面积分别记为、、,若=2,则+= .
16. (2019?泸州)如图,在等腰中,,,点在边上,,点在边上,,垂足为,则长为__________.
三、解答题
17. (2020·杭州)如图,在中,点D,E,F分别在AB,BC,AC边上,,.
(1)求证:.
(2)设,
①若BC=12,求线段BE的长;
②若△EFC的面积是20,求△ABC的面积.
18. 如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC、CD于点P、Q.
(1)请写出图中各对相似三角形(相似比为1除外);
(2)求BP∶PQ∶QR.
19. (2020·攀枝花)三角形三条边上的中线交于一点,这个点叫三角形的重心.如图是的重心.求证:.
20. (2020·南京)如图,在△ABC和△A’B’C’中,D、D’分别是AB、A’B’上一点,=.
(1)当==时,求证:△ABC∽△A’B’C’.
证明的途径可以用下面的框图表示,请填写其中的空格.
(2)当==时,判断△ABC与△A’B’C’是否相似,并说明理由.
人教版 九年级数学下册 第二十七章 相似 章末训练-答案
一、选择题
1. 【答案】 D
【解析】本题考查了相似三角形的判定与性质,解答本题的关键是得出DE是中位线,从而判断△ADE∽△ABC,然后掌握相似三角形的面积比等于相似比的平方即可求解本题.首先判断出△ADE∽△ABC,然后根据相似三角形的面积比等于相似比的平方即可求出△ABC的面积.
根据题意,点D和点E分别是AB和AC的中点,则DE∥BC且DE=BC,故可以判断出△ADE∽△ABC,根据相似三角形的面积比等于相似比的平方,可知:=1:4,则:=3:4,题中已知,故可得=5,=20,因此本题选D.
2. 【答案】B
【解析】本题考查了在坐标系中,位似图形点的坐标.在平面直角坐标系中,如果以原点为位似中心,画出一个与原图形位似的图形,使它与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(–kx,–ky).由A(4,3),位似比k=,可得C()因此本题选B.
3. 【答案】B
【解析】A、如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为4∶9,是假命题;
B、如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为4∶9,是真命题;
C、如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为16∶81,是假命题;
D、如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为16∶81,是假命题,
故选B.
4. 【答案】 B.
【解析】利用平行四边形的性质可得出点O为线段BD的中点,结合点E是CD的中点可得出线段OE为△DBC的中位线,利用三角形中位线定理可得出OE∥BC,OE=BC,进而可得出△DOE∽△DBC,再利用相似三角形的面积比等于相似比的平分,即可求出△DEO与△BCD的面积的比为1:4.
5. 【答案】A
【解析】利用平行截割定理求的值.∵DE∥AB,∴==,∵CE+AE=AC,∴=.
6. 【答案】D
【解析】设,∵,∴,
∵四边形ABCD是平行四边形,∴,,
∵点F是BC的中点,∴,
∵,∴,
∴,故选D.
7. 【答案】C
【解析】设,,∴,
∵,∴,
∴,∴,
∴,,
∵,,∴,
∵,∴,
∴,
设,,∴,
∴,∴,∴,
故选C.
8. 【答案】C
【解析】∵四边形EFGH为正方形,∴∠EGH=45°,∠FGH=90°,∵OG=GP,∴∠GOP=∠OPG=67.5°,∴∠PBG=22.5°,又∵∠DBC=45°,∴∠GBC=22.5°,∴∠PBG=∠GBC,
∵∠BGP=∠BG=90°,BG=BG,∴△BPG≌△BCG,∴PG=CG.设OG=PG=CG=x,
∵O为EG,BD的交点,∴EG=2x,FGx.∵四个全等的直角三角形拼成“赵爽弦图”,∴BF=CG=x,
∴BG=xx,∴BC2=BG2+CG2,
∴,因此本题选D.
二、填空题
9. 【答案】
【解析】∵,∴,
故2y=x,则,故答案为:.
10. 【答案】18
【解析】∵与是以坐标原点为位似中心的位似图形,
若点,,∴位似比为,
∵,,
∴,
∴的面积为:,
故答案为:18.
11. 【答案】2
【解析】∵BC∥DE,∴△ADE∽△ABC,∴ ,设DE=x,则AB=10-x∵AD=BC=4,∴,∴x1=8 ,x2=2(舍去), ,此本题答案为2 .
12. 【答案】
【解析】点,分别是边,的中点,
,即
又,
则四边形的面积为.
故答案为:.
13. 【答案】
【解析】∵点F是△ABC的重心,∴BF=2EF,∴BE=3EF,
∵FG∥BC,∴△EFG∽△EBC,
∴,()2,
∴S1∶S2,故答案为:.
14. 【答案】(1)△ABC如图 (2)直角三角形 解析:(1)因为点A的坐标为(1,2),所以点A关于y轴的对称点B的坐标为(-1,2),关于原点的对称点C的坐标为(-1,-2).连AB,BC,AC,作△ABC.
设AB交y轴于D点,如图,
D点坐标为(0,2),
∵OD∥BC,
∴△ADO∽△ABC.
∴==.
(2)∵ab≠0,∴a≠0,且b≠0,
∴点A不在坐标轴上,
∴AB∥x轴,BC⊥x轴.
∴∠ABC=90°.
∴△ABC是直角三角形.
15. 【答案】18
【解析】本题考查了相似三角形的判定、性质,三角形的面积,解题的关键是根据已知条件推出相似三角形,并由相似比得到面积比.
∵PA=3PE,PD=3PF,∠APD =∠EPF,∴△PEF∽△PAD,相似比为1︰3,
∵△PEF的面积为=2,∴=9S=9×2=18,
∴+==18.
16. 【答案】
【解析】如图,过作于,则∠AHD=90°,
∵在等腰中,,,
∴,,
∴∠ADH=90°–∠CAD=45°=∠CAD,
∴,
∴CH=AC–AH=15–DH,
∵,∴,
又∵∠ANH=∠DNF,∴,
∴,∴,
∵,CE+BE=BC=15,∴,
∴,
∴,
∴,故答案为:.
三、解答题
17. 【答案】
解: (1)∵DE∥AC,∴∠BED=∠C.∵EF∥AB,∴∠B=∠FEC,∴△BDE∽△EFC.
(2)①∵EF∥AB,∴==.∵BC=12,∴=,∴BE=4.
②∵EF∥AB,∴△EFC△BAC,∴=.∵=,∴=.又∵△EFC的面积是20,∴=,∴S△ABC=45,即△ABC的面积是45.
18. 【答案】
解:(1)△BCP∽△BER,△PCQ∽△PAB,△PCQ∽△RDQ,△PAB∽△RDQ.
(2)∵四边形ABCD和四边形ACED都是平行四边形,
∴BC=AD=CE,AC∥DE,∴PB=PR,=.
又∵PC∥DR,∴△PCQ∽△RDQ.
∵点R是DE的中点,∴DR=RE.
∴===,∴QR=2PQ.
又∵BP=PR=PQ+QR=3PQ,
∴BP∶PQ∶QR=3∶1∶2.
19. 【答案】
证明:连接DE,
∵点G是△ABC的重心,
∴点E和点D分别是AB和BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC且DE=AC,
∴△DEG∽△ACG,
∴,
∴
∴AD=3DG,
即AD=3GD.
20. 【答案】
解:(1) == ∠A=∠A’.
(2)如图,过点D、D’分别作DE∥BC,D’E’∥B’C’,DE交AC于点E,D’E’交A’C’于点E’.
∵DE∥BC,
∴△ADE∽△ABC.
∴==.
同理==.
又=,
∴=,
∴=.
同理 =.
∴=,即=.
∴=.
又==,
∴==,
∴△DCE∽△D’C’E’.
∴∠CED=∠C’E’D’.
∵DE∥BC,
∴∠CED+∠ACB=180°.
同理 ∠C’E’D’+∠A’C’B’=180°.
∴∠ACB=∠A’C’B’.
又=
∴△ABC∽△A’B’C’.
