3.3 垂径定理同步练习(含解析)
图片预览



文档简介
3.3垂径定理
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,其中选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2019秋?金平区期末)下列语句,错误的是( )
A.直径是弦
B.相等的圆心角所对的弧相等
C.弦的垂直平分线一定经过圆心
D.平分弧的半径垂直于弧所对的弦
2.(2019春?西湖区校级月考)如图,⊙O的直径CD=10,AB是⊙O的弦,AB⊥CD于M,且DM:MC=4:1,则AB的长是( )
A.2 B.8 C.16 D.91
3.(2019秋?兴国县期末)如图,⊙O的弦AB⊥OC,且OD=2DC,AB=25,则⊙O的半径为( )
A.1 B.2 C.3 D.9
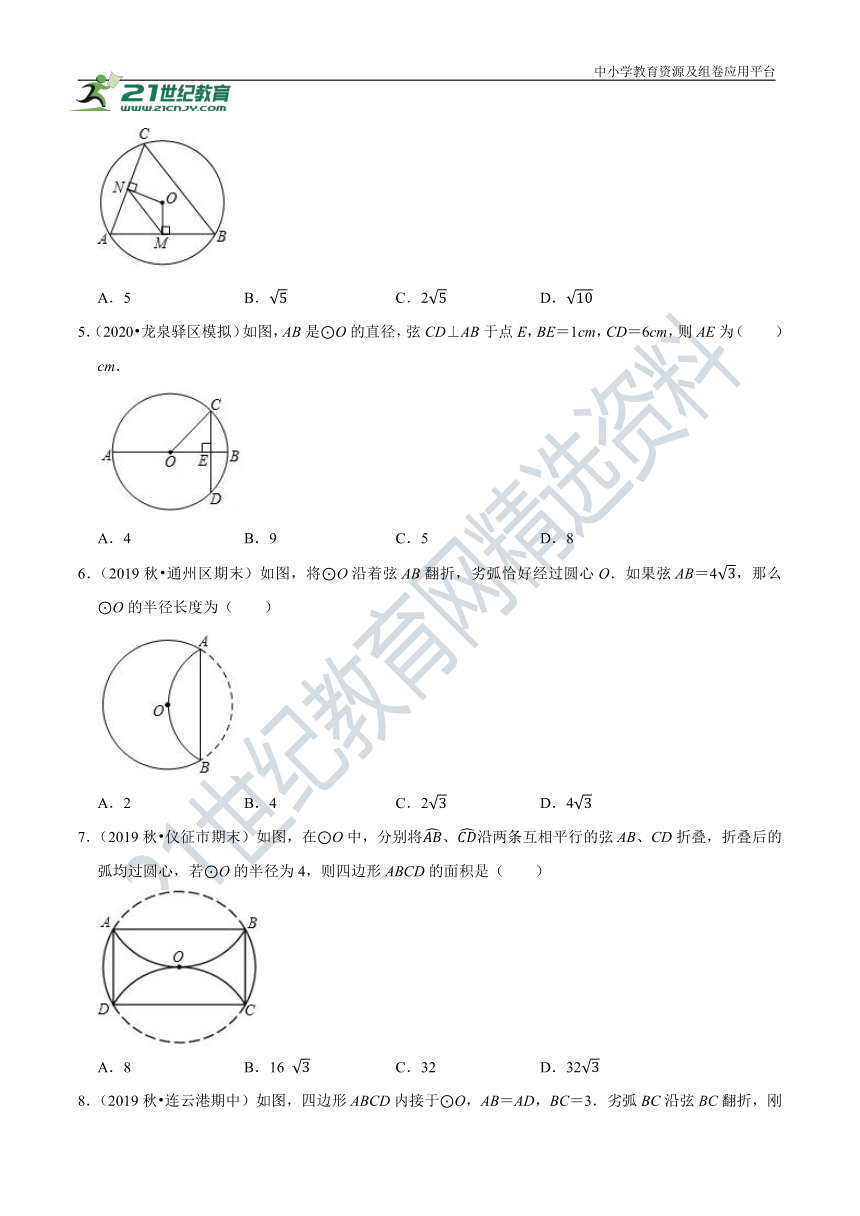
4.(2019秋?天津期末)如图,已知AB、AC都是⊙O的弦,OM⊥AB,ON⊥AC,垂足分别为M,N,若MN=5,那么BC等于( )
A.5 B.5 C.25 D.10
5.(2020?龙泉驿区模拟)如图,AB是⊙O的直径,弦CD⊥AB于点E,BE=1cm,CD=6cm,则AE为( )cm.
A.4 B.9 C.5 D.8
6.(2019秋?通州区期末)如图,将⊙O沿着弦AB翻折,劣弧恰好经过圆心O.如果弦AB=43,那么⊙O的半径长度为( )
A.2 B.4 C.23 D.43
7.(2019秋?仪征市期末)如图,在⊙O中,分别将AB、CD沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,若⊙O的半径为4,则四边形ABCD的面积是( )
A.8 B.16 3 C.32 D.323
8.(2019秋?连云港期中)如图,四边形ABCD内接于⊙O,AB=AD,BC=3.劣弧BC沿弦BC翻折,刚好经过圆心O.当对角线BD最大时,则弦AB的长是( )
A.6 B.23 C.32 D.22
9.(2020?浙江自主招生)如图,将半径为4cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长度为( )
A.4cm B.23cm C.43cm D.(2+43)cm
10.(2018?高邮市一模)如图,已知⊙O的半径为5,AB是⊙O的弦,AB=8,Q为AB中点,P是圆上的一点(不与A、B重合),连接PQ,则PQ的最小值为( )
A.1 B.2 C.3 D.8
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2019秋?黄岩区期末)如图,⊙O的直径CD长为6,点E是直径CD上一点,且CE=1,过点E作弦AB⊥CD,则弦AB长为 .
12.(2020秋?梁溪区期中)把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=12cm,则球的半径为 cm.
13.(2020秋?西城区校级期中)筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,则筒车工作时,盛水桶在水面以下的最大深度为 m.
14.(2019秋?顺义区期末)如图,⊙O的直径AB=10,弦CD⊥AB于点E,若BE=2,则CD的长为 .
15.(2019秋?瑞安市期中)一面墙上有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图,若矩形的高为2m,宽为233m,则要打掉墙体的面积为 m2.
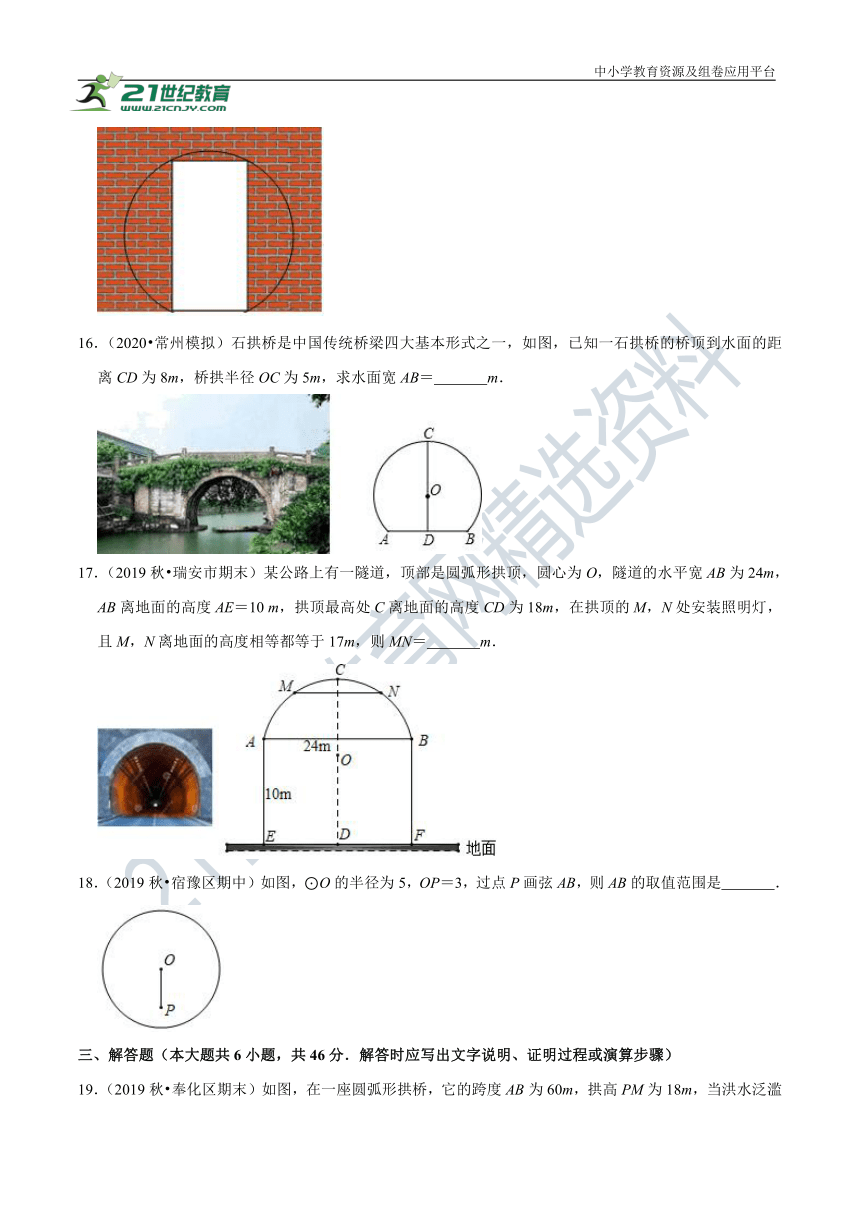
16.(2020?常州模拟)石拱桥是中国传统桥梁四大基本形式之一,如图,已知一石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,求水面宽AB= m.
17.(2019秋?瑞安市期末)某公路上有一隧道,顶部是圆弧形拱顶,圆心为O,隧道的水平宽AB为24m,AB离地面的高度AE=10 m,拱顶最高处C离地面的高度CD为18m,在拱顶的M,N处安装照明灯,且M,N离地面的高度相等都等于17m,则MN= m.
18.(2019秋?宿豫区期中)如图,⊙O的半径为5,OP=3,过点P画弦AB,则AB的取值范围是 .
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2019秋?奉化区期末)如图,在一座圆弧形拱桥,它的跨度AB为60m,拱高PM为18m,当洪水泛滥到跨度只有30m时,就要采取紧急措施,若某次洪水中,拱顶离水面只有4m,即PN=4m时,试通过计算说明是否需要采取紧急措施.
20.(2019秋?东城区校级期中)如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,如图EM经过圆心交⊙O于点E,EM⊥CD,并且CD=4cm,EM=6cm,求⊙O的半径.
21.如图,正方形ABCD内接于⊙O,M为AD的中点,连接BM,CM,求证:BM=CM.
22.(2019秋?海淀区期中)如图,一条公路的转弯处是一段圆弧(AB),点O是这段弧所在圆的圆心.AB=100m,C是AB上一点,OC⊥AB,垂足为D,CD=10m,求这段弯路的半径.
23.(2019秋?东台市期中)如图,在⊙O中,直径为MN,正方形ABCD的四个顶点分别在半径OM、OP以及⊙O上,并且∠POM=45°,若AB=1.
(1)求OD的长;
(2)求⊙O的半径.
24.(2017秋?农安县校级期中)如图,在平面直角坐标系中,点M在x轴的正半轴上,⊙M交x轴于A,B两点,交y轴于C,D两点,且C为弧AE的中点,连接CE、AE、CB、EB、AE与y轴交于点F,已知A(﹣2,0)、C(0,4).
(1)求证:AF=CF;
(2)求⊙M的半径及EB的长.
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解析】直径是弦,A正确,不符合题意;
在同圆或等圆中,相等的圆心角所对的弧相等,B错误,符合题意;
弦的垂直平分线一定经过圆心,C正确,不符合题意;
平分弧的半径垂直于弧所对的弦,D正确,不符合题意;
故选:B.
2.【解析】连接OA,如图,
∵DC⊥AB,且DC为圆O的直径,
∴M为AB中点,即AM=BM=12AB,
又∵CD=10,DM:MC=4:1,
∴DM=45DC=8,MC=15DC=2,且OA=OD=5,
∴OM=DM﹣OD=8﹣5=3,
在Rt△AOM中,根据勾股定理得:OA2=OM2+AM2,
即AM=OA2-OM2=4,
则AB=2AM=8.
故选:B.
3.【解析】设OD=2a,则CD=a,OA=3a,
∵AB⊥OC,OC为半径,
∴AD=BD=12AB=5,
在Rt△ODA中,由勾股定理得:(3a)2=(2a)2+(5)2,
a=1(负数舍去),
OA=3×1=3,
故选:C.
4.【解析】∵OM⊥AB,ON⊥AC,垂足分别为M、N,
∴M、N分别是AB与AC的中点,
∴MN是△ABC的中位线,
∴BC=2MN=25,
故选:C.
5.【解析】设OC=OB=xcm,
∵AB⊥CD,AB是直径,
∴EC=DE=3cm,
在Rt△OEC中,∵OC2=CE2+OE2,
∴x2=32+(x﹣1)2,
∴x=5,
∴OE=4cm,
∴AE=OA+OE=5+4=9cm,
故选:B.
6.【解析】作OD⊥AB于D,连接OA.
∵OD⊥AB,AB=43,
∴AD=12AB=23,
由折叠得:OD=12AO,
设OD=x,则AO=2x,
在Rt△OAD中,AD2+OD2=OA2,
(23)2+x2=(2x)2,
x=2,
∴OA=2x=4,即⊙O的半径长度为4;
故选:B.
7.【解析】过O作OH⊥AB交⊙O于E,反向延长EO交CD于G,交⊙O于F,
连接OA,OB,OD,
∵AB∥CD,
∴EF⊥CD,
∵分别将AB、CD沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,
∴OH=12OA,
∴∠HAO=30°,
∴∠AOH=60°,
同理∠DOG=60°,
∴∠AOD=60°,
∴△AOD是等边三角形,
∵OA=OB,
∴∠ABO=∠BAO=30°,
∴∠AOB=120°,
∴∠AOD+∠AOB=180°,
∴D,O,B三点共线,且BD为⊙O的直径,
∴∠DAB=90°,
同理,∠ABC=∠ADC=90°,
∴四边形ABCD是矩形,
∴AD=AO=4,AB=3AD=43,
∴四边形ABCD的面积是163,
故选:B.
8.【解析】作OH⊥BC于H,连接OB,如图,则BH=CH=12BC=32,
∵劣弧BC沿弦BC翻折,刚好经过圆心O,
∴OH=12OB,
∴∠OBH=30°,
∴OH=33BH=32,
∴OB=2OH=3,
当BD为直径时,即BD=23时,对角线BD最大,则此时∠BAD=90°,
∵AB=AD,
∴此时△ABD为等腰直角三角形,
∴AB=22BD=22×23=6.
故选:A.
9.【解析】过O作OC⊥AB,交圆O于点D,连接OA,
∴C为AB中点,即AC=BC,
由折叠得到CD=OC=12OD=2cm,
在Rt△AOC中,根据勾股定理得:AC2+OC2=OA2,
即AC2+4=16,
解得:AC=23cm,
则AB=2AC=43cm.
故选:C.
10.【解析】由题意得,当点P为劣弧AB的中点时,PQ最小,
连接OP、OA,
由垂径定理得,点Q在OP上,AQ=12AB=4,
在Rt△AOB中,OQ=OA2-AQ2=3,
∴PQ=OP﹣OQ=2,
故选:B.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解析】连接OA,∵AB⊥CD,
∴AE=BE
∵CE=1,OA=OC=3
∴OE=3﹣1=2,
在Rt△AOE中,AE=OA2-OE2=32-22=5
∴AB=25,
故答案为25.
12.【解析】EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDMN是矩形,
∴MN=CD=12,
设OF=xcm,则ON=OF,
∴OM=MN﹣ON=12﹣x,MF=6,
在直角三角形OMF中,OM2+MF2=OF2
即:(12﹣x)2+62=x2
解得:x=7.5,
故答案为:7.5.
13.【解析】过O点作半径OD⊥AB于E,如图,
∴AE=BE=12AB=12×8=4,
在Rt△AEO中,OE=OA2-AE2=52-42=3,
∴ED=OD﹣OE=5﹣3=2(m),
答:筒车工作时,盛水桶在水面以下的最大深度为2m.
14.【解析】如图,连接OC.
∵⊙O的直径AB=10,
∴OB=OC=5,
∴OE=OB﹣BE=5﹣2=3,
∵弦CD⊥AB于点E,
∴CE=ED=12CD.
∵在Rt△OEC中,∠OEC=90°,OE=3,OC=5,
∴CE=OC2-OE2=52-32=4,
∴CD=2CE=8.
故答案为8.
15.【解析】如图,连结AD、BC交于O,∵∠BDC=90°,
∴BC是直径,
∴BC=BD2+CD2=22+(233)2=433,
∴OA=OB=AB=233,
∴△AOB是正三角形,
∴∠AOB=60°,∠AOC=120°,
∴S△AOB=33,S△AOC=33,
∴S=2(S扇形OAC﹣S△AOC)+S扇形OAB﹣S△AOB
=2[120?π×(233)2360-33]+[60?π×(233)2360-33]
=109π-3,
∴打掉墙体面积为(109π-3)平方米,
故答案为:(109π-3).
16.【解析】连接OA,如图所示.
∵CD⊥AB,
∴AD=BD=12AB.
在Rt△ADO中,OA=OC=5m,OD=CD﹣OC=3m,∠ADO=90°,
∴AD=OA2-OD2=52-32=4(m),
∴AB=2AD=8m.
故答案为:8.
17.【解析】设CD于AB交于G,与MN交于H,
∵CD=18m,AE=10m,AB=24m,HD=17m,
∴CG=8m,AG=12m,CH=1m,
设圆拱的半径为r,
在Rt△AOG中,OA2=OG2+AG2,
∴r2=(r﹣8)2+122,
解得r=13,
∴OC=13m,
∴OH=13﹣1=12m,
在Rt△MOH中,OM2=OH2+MH2,
∴132=122+MH2,
解得MH2=25,
∴MH=5m,
∴MN=10m,
故答案为10.
18.【解析】过点P作CD⊥OP,交⊙O于C,D.连接OC.
∵OC=5,OP=3,∠OPC=90°,
∴PC=OC2-OP2=52-32=4,
∵OP⊥CD,
∴PC=PD=4,
∴CD=8,
∴过点P的最短的弦长为8,最长的弦长为10,
即AB的取值范围是8≤AB≤10,
故答案为:8≤AB≤10.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解析】设圆弧所在圆的圆心为O,连接OA、OA′,设半径为x米,
则OA=OA′=OP,
由垂径定理可知AM=BM,A′N=B′N,
∵AB=60米,
∴AM=30米,且OM=OP﹣PM=(x﹣18)米,
在Rt△AOM中,由勾股定理可得AO2=OM2+AM2,
即x2=(x﹣18)2+302,解得x=34,
∴ON=OP﹣PN=34﹣4=30(米),
在Rt△A′ON中,由勾股定理可得A′N=OA'2-ON2=342-302=16(米),
∴A′B′=32米>30米,
∴不需要采取紧急措施.
20.【解析】连接OC,
∵M是⊙O弦CD的中点,
根据垂径定理:EM⊥CD,
又CD=4则有:CM=12CD=2,
设圆的半径是x米,
在Rt△COM中,有OC2=CM2+OM2,
即:x2=22+(6﹣x)2,
解得:x=103,
所以圆的半径长是103cm.
21.【解答】证明:∵四边形ABCD是正方形,
∴AB=CD,
∴AB=CD,
∵M为AD中点,
∴AM=DM,
∴AB+AM=CD+DM,即BM=CM,
∴BM=CM.
22.【解析】设这段弯路的半径为r m,
∵OC⊥AB于D,AB=100(m),
∴BD=DA=12AB=50(m)
∴CD=10(m),
得OD=r﹣10(m).
∵Rt△BOD中,根据勾股定理有BO2=BD2+DO2
即r2=502+(r﹣10)2
解得r=130(m).
答:这段弯路的半径为130 m.
23.【解析】(1)如图,
∵四边形ABCD 为正方形,
∴DC=BC=AB=1,∠DCO=∠ABC=90°,
∵∠DCO=45°,
∴CO=DC=1,
∴OD=2CO=2×1=2;
(2)BO=BC+CO=BC+CD1+1=2,.
连接AO,
则△ABO 为直角三角形,
于是 AO=AB2+BO2=12+22=5.
即⊙O的半径为5.
24.【解答】(1)证明:∵AB⊥CD,
∴AC=AD,OC=OD=4,
C为弧AE的中点,
∴AC=CE=AD,
∴∠CAD=∠CAE,
∴AF=CF;
(2)解:连接DM,如图,
设⊙M的半径为r,则OM=r﹣2,DM=r,
在Rt△ODM中,(r﹣2)2+42=r2,解得r=5,
设OF=x,则CF=AF=4﹣x,
在Rt△AOF中,22+x2=(4﹣x)2,解得x=32,
∴AF=4-32=52,
∵∠OAF=∠EAB,
而∠AOF=∠AEB,
∴Rt△AOF∽Rt△AEB,
∴OF:BE=AF:AB,即32:BE=52:10,解得BE=6,
∴⊙M的半径为5,EB的长为6.
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,其中选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2019秋?金平区期末)下列语句,错误的是( )
A.直径是弦
B.相等的圆心角所对的弧相等
C.弦的垂直平分线一定经过圆心
D.平分弧的半径垂直于弧所对的弦
2.(2019春?西湖区校级月考)如图,⊙O的直径CD=10,AB是⊙O的弦,AB⊥CD于M,且DM:MC=4:1,则AB的长是( )
A.2 B.8 C.16 D.91
3.(2019秋?兴国县期末)如图,⊙O的弦AB⊥OC,且OD=2DC,AB=25,则⊙O的半径为( )
A.1 B.2 C.3 D.9
4.(2019秋?天津期末)如图,已知AB、AC都是⊙O的弦,OM⊥AB,ON⊥AC,垂足分别为M,N,若MN=5,那么BC等于( )
A.5 B.5 C.25 D.10
5.(2020?龙泉驿区模拟)如图,AB是⊙O的直径,弦CD⊥AB于点E,BE=1cm,CD=6cm,则AE为( )cm.
A.4 B.9 C.5 D.8
6.(2019秋?通州区期末)如图,将⊙O沿着弦AB翻折,劣弧恰好经过圆心O.如果弦AB=43,那么⊙O的半径长度为( )
A.2 B.4 C.23 D.43
7.(2019秋?仪征市期末)如图,在⊙O中,分别将AB、CD沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,若⊙O的半径为4,则四边形ABCD的面积是( )
A.8 B.16 3 C.32 D.323
8.(2019秋?连云港期中)如图,四边形ABCD内接于⊙O,AB=AD,BC=3.劣弧BC沿弦BC翻折,刚好经过圆心O.当对角线BD最大时,则弦AB的长是( )
A.6 B.23 C.32 D.22
9.(2020?浙江自主招生)如图,将半径为4cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长度为( )
A.4cm B.23cm C.43cm D.(2+43)cm
10.(2018?高邮市一模)如图,已知⊙O的半径为5,AB是⊙O的弦,AB=8,Q为AB中点,P是圆上的一点(不与A、B重合),连接PQ,则PQ的最小值为( )
A.1 B.2 C.3 D.8
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2019秋?黄岩区期末)如图,⊙O的直径CD长为6,点E是直径CD上一点,且CE=1,过点E作弦AB⊥CD,则弦AB长为 .
12.(2020秋?梁溪区期中)把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=12cm,则球的半径为 cm.
13.(2020秋?西城区校级期中)筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,则筒车工作时,盛水桶在水面以下的最大深度为 m.
14.(2019秋?顺义区期末)如图,⊙O的直径AB=10,弦CD⊥AB于点E,若BE=2,则CD的长为 .
15.(2019秋?瑞安市期中)一面墙上有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图,若矩形的高为2m,宽为233m,则要打掉墙体的面积为 m2.
16.(2020?常州模拟)石拱桥是中国传统桥梁四大基本形式之一,如图,已知一石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,求水面宽AB= m.
17.(2019秋?瑞安市期末)某公路上有一隧道,顶部是圆弧形拱顶,圆心为O,隧道的水平宽AB为24m,AB离地面的高度AE=10 m,拱顶最高处C离地面的高度CD为18m,在拱顶的M,N处安装照明灯,且M,N离地面的高度相等都等于17m,则MN= m.
18.(2019秋?宿豫区期中)如图,⊙O的半径为5,OP=3,过点P画弦AB,则AB的取值范围是 .
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2019秋?奉化区期末)如图,在一座圆弧形拱桥,它的跨度AB为60m,拱高PM为18m,当洪水泛滥到跨度只有30m时,就要采取紧急措施,若某次洪水中,拱顶离水面只有4m,即PN=4m时,试通过计算说明是否需要采取紧急措施.
20.(2019秋?东城区校级期中)如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,如图EM经过圆心交⊙O于点E,EM⊥CD,并且CD=4cm,EM=6cm,求⊙O的半径.
21.如图,正方形ABCD内接于⊙O,M为AD的中点,连接BM,CM,求证:BM=CM.
22.(2019秋?海淀区期中)如图,一条公路的转弯处是一段圆弧(AB),点O是这段弧所在圆的圆心.AB=100m,C是AB上一点,OC⊥AB,垂足为D,CD=10m,求这段弯路的半径.
23.(2019秋?东台市期中)如图,在⊙O中,直径为MN,正方形ABCD的四个顶点分别在半径OM、OP以及⊙O上,并且∠POM=45°,若AB=1.
(1)求OD的长;
(2)求⊙O的半径.
24.(2017秋?农安县校级期中)如图,在平面直角坐标系中,点M在x轴的正半轴上,⊙M交x轴于A,B两点,交y轴于C,D两点,且C为弧AE的中点,连接CE、AE、CB、EB、AE与y轴交于点F,已知A(﹣2,0)、C(0,4).
(1)求证:AF=CF;
(2)求⊙M的半径及EB的长.
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解析】直径是弦,A正确,不符合题意;
在同圆或等圆中,相等的圆心角所对的弧相等,B错误,符合题意;
弦的垂直平分线一定经过圆心,C正确,不符合题意;
平分弧的半径垂直于弧所对的弦,D正确,不符合题意;
故选:B.
2.【解析】连接OA,如图,
∵DC⊥AB,且DC为圆O的直径,
∴M为AB中点,即AM=BM=12AB,
又∵CD=10,DM:MC=4:1,
∴DM=45DC=8,MC=15DC=2,且OA=OD=5,
∴OM=DM﹣OD=8﹣5=3,
在Rt△AOM中,根据勾股定理得:OA2=OM2+AM2,
即AM=OA2-OM2=4,
则AB=2AM=8.
故选:B.
3.【解析】设OD=2a,则CD=a,OA=3a,
∵AB⊥OC,OC为半径,
∴AD=BD=12AB=5,
在Rt△ODA中,由勾股定理得:(3a)2=(2a)2+(5)2,
a=1(负数舍去),
OA=3×1=3,
故选:C.
4.【解析】∵OM⊥AB,ON⊥AC,垂足分别为M、N,
∴M、N分别是AB与AC的中点,
∴MN是△ABC的中位线,
∴BC=2MN=25,
故选:C.
5.【解析】设OC=OB=xcm,
∵AB⊥CD,AB是直径,
∴EC=DE=3cm,
在Rt△OEC中,∵OC2=CE2+OE2,
∴x2=32+(x﹣1)2,
∴x=5,
∴OE=4cm,
∴AE=OA+OE=5+4=9cm,
故选:B.
6.【解析】作OD⊥AB于D,连接OA.
∵OD⊥AB,AB=43,
∴AD=12AB=23,
由折叠得:OD=12AO,
设OD=x,则AO=2x,
在Rt△OAD中,AD2+OD2=OA2,
(23)2+x2=(2x)2,
x=2,
∴OA=2x=4,即⊙O的半径长度为4;
故选:B.
7.【解析】过O作OH⊥AB交⊙O于E,反向延长EO交CD于G,交⊙O于F,
连接OA,OB,OD,
∵AB∥CD,
∴EF⊥CD,
∵分别将AB、CD沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,
∴OH=12OA,
∴∠HAO=30°,
∴∠AOH=60°,
同理∠DOG=60°,
∴∠AOD=60°,
∴△AOD是等边三角形,
∵OA=OB,
∴∠ABO=∠BAO=30°,
∴∠AOB=120°,
∴∠AOD+∠AOB=180°,
∴D,O,B三点共线,且BD为⊙O的直径,
∴∠DAB=90°,
同理,∠ABC=∠ADC=90°,
∴四边形ABCD是矩形,
∴AD=AO=4,AB=3AD=43,
∴四边形ABCD的面积是163,
故选:B.
8.【解析】作OH⊥BC于H,连接OB,如图,则BH=CH=12BC=32,
∵劣弧BC沿弦BC翻折,刚好经过圆心O,
∴OH=12OB,
∴∠OBH=30°,
∴OH=33BH=32,
∴OB=2OH=3,
当BD为直径时,即BD=23时,对角线BD最大,则此时∠BAD=90°,
∵AB=AD,
∴此时△ABD为等腰直角三角形,
∴AB=22BD=22×23=6.
故选:A.
9.【解析】过O作OC⊥AB,交圆O于点D,连接OA,
∴C为AB中点,即AC=BC,
由折叠得到CD=OC=12OD=2cm,
在Rt△AOC中,根据勾股定理得:AC2+OC2=OA2,
即AC2+4=16,
解得:AC=23cm,
则AB=2AC=43cm.
故选:C.
10.【解析】由题意得,当点P为劣弧AB的中点时,PQ最小,
连接OP、OA,
由垂径定理得,点Q在OP上,AQ=12AB=4,
在Rt△AOB中,OQ=OA2-AQ2=3,
∴PQ=OP﹣OQ=2,
故选:B.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解析】连接OA,∵AB⊥CD,
∴AE=BE
∵CE=1,OA=OC=3
∴OE=3﹣1=2,
在Rt△AOE中,AE=OA2-OE2=32-22=5
∴AB=25,
故答案为25.
12.【解析】EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDMN是矩形,
∴MN=CD=12,
设OF=xcm,则ON=OF,
∴OM=MN﹣ON=12﹣x,MF=6,
在直角三角形OMF中,OM2+MF2=OF2
即:(12﹣x)2+62=x2
解得:x=7.5,
故答案为:7.5.
13.【解析】过O点作半径OD⊥AB于E,如图,
∴AE=BE=12AB=12×8=4,
在Rt△AEO中,OE=OA2-AE2=52-42=3,
∴ED=OD﹣OE=5﹣3=2(m),
答:筒车工作时,盛水桶在水面以下的最大深度为2m.
14.【解析】如图,连接OC.
∵⊙O的直径AB=10,
∴OB=OC=5,
∴OE=OB﹣BE=5﹣2=3,
∵弦CD⊥AB于点E,
∴CE=ED=12CD.
∵在Rt△OEC中,∠OEC=90°,OE=3,OC=5,
∴CE=OC2-OE2=52-32=4,
∴CD=2CE=8.
故答案为8.
15.【解析】如图,连结AD、BC交于O,∵∠BDC=90°,
∴BC是直径,
∴BC=BD2+CD2=22+(233)2=433,
∴OA=OB=AB=233,
∴△AOB是正三角形,
∴∠AOB=60°,∠AOC=120°,
∴S△AOB=33,S△AOC=33,
∴S=2(S扇形OAC﹣S△AOC)+S扇形OAB﹣S△AOB
=2[120?π×(233)2360-33]+[60?π×(233)2360-33]
=109π-3,
∴打掉墙体面积为(109π-3)平方米,
故答案为:(109π-3).
16.【解析】连接OA,如图所示.
∵CD⊥AB,
∴AD=BD=12AB.
在Rt△ADO中,OA=OC=5m,OD=CD﹣OC=3m,∠ADO=90°,
∴AD=OA2-OD2=52-32=4(m),
∴AB=2AD=8m.
故答案为:8.
17.【解析】设CD于AB交于G,与MN交于H,
∵CD=18m,AE=10m,AB=24m,HD=17m,
∴CG=8m,AG=12m,CH=1m,
设圆拱的半径为r,
在Rt△AOG中,OA2=OG2+AG2,
∴r2=(r﹣8)2+122,
解得r=13,
∴OC=13m,
∴OH=13﹣1=12m,
在Rt△MOH中,OM2=OH2+MH2,
∴132=122+MH2,
解得MH2=25,
∴MH=5m,
∴MN=10m,
故答案为10.
18.【解析】过点P作CD⊥OP,交⊙O于C,D.连接OC.
∵OC=5,OP=3,∠OPC=90°,
∴PC=OC2-OP2=52-32=4,
∵OP⊥CD,
∴PC=PD=4,
∴CD=8,
∴过点P的最短的弦长为8,最长的弦长为10,
即AB的取值范围是8≤AB≤10,
故答案为:8≤AB≤10.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解析】设圆弧所在圆的圆心为O,连接OA、OA′,设半径为x米,
则OA=OA′=OP,
由垂径定理可知AM=BM,A′N=B′N,
∵AB=60米,
∴AM=30米,且OM=OP﹣PM=(x﹣18)米,
在Rt△AOM中,由勾股定理可得AO2=OM2+AM2,
即x2=(x﹣18)2+302,解得x=34,
∴ON=OP﹣PN=34﹣4=30(米),
在Rt△A′ON中,由勾股定理可得A′N=OA'2-ON2=342-302=16(米),
∴A′B′=32米>30米,
∴不需要采取紧急措施.
20.【解析】连接OC,
∵M是⊙O弦CD的中点,
根据垂径定理:EM⊥CD,
又CD=4则有:CM=12CD=2,
设圆的半径是x米,
在Rt△COM中,有OC2=CM2+OM2,
即:x2=22+(6﹣x)2,
解得:x=103,
所以圆的半径长是103cm.
21.【解答】证明:∵四边形ABCD是正方形,
∴AB=CD,
∴AB=CD,
∵M为AD中点,
∴AM=DM,
∴AB+AM=CD+DM,即BM=CM,
∴BM=CM.
22.【解析】设这段弯路的半径为r m,
∵OC⊥AB于D,AB=100(m),
∴BD=DA=12AB=50(m)
∴CD=10(m),
得OD=r﹣10(m).
∵Rt△BOD中,根据勾股定理有BO2=BD2+DO2
即r2=502+(r﹣10)2
解得r=130(m).
答:这段弯路的半径为130 m.
23.【解析】(1)如图,
∵四边形ABCD 为正方形,
∴DC=BC=AB=1,∠DCO=∠ABC=90°,
∵∠DCO=45°,
∴CO=DC=1,
∴OD=2CO=2×1=2;
(2)BO=BC+CO=BC+CD1+1=2,.
连接AO,
则△ABO 为直角三角形,
于是 AO=AB2+BO2=12+22=5.
即⊙O的半径为5.
24.【解答】(1)证明:∵AB⊥CD,
∴AC=AD,OC=OD=4,
C为弧AE的中点,
∴AC=CE=AD,
∴∠CAD=∠CAE,
∴AF=CF;
(2)解:连接DM,如图,
设⊙M的半径为r,则OM=r﹣2,DM=r,
在Rt△ODM中,(r﹣2)2+42=r2,解得r=5,
设OF=x,则CF=AF=4﹣x,
在Rt△AOF中,22+x2=(4﹣x)2,解得x=32,
∴AF=4-32=52,
∵∠OAF=∠EAB,
而∠AOF=∠AEB,
∴Rt△AOF∽Rt△AEB,
∴OF:BE=AF:AB,即32:BE=52:10,解得BE=6,
∴⊙M的半径为5,EB的长为6.
