3.5 确定圆的条件同步练习(含解析)
文档属性
| 名称 | 3.5 确定圆的条件同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 10:11:55 | ||
图片预览




文档简介
3.5确定圆的条件
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,其中选择10道、填空6道、解答8道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2019秋?北仑区期末)下列四个结论,不正确的是( )
①过三点可以作一个圆;
②圆内接四边形对角相等;
③平分弦的直径垂直于弦;
④相等的圆周角所对的弧也相等.
A.②③ B.①③④ C.①②④ D.①②③④
2.(2020秋?崇川区校级月考)下列语句中正确的有( )
①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③圆的轴对称图形,任何一条直径所在直线都是它的对称轴;④三点确定一个圆.
A.1个 B.2个 C.3个 D.4个
3.(2019?吴兴区校级一模)平面上有四个点,过其中任意3个点一共能确定圆的个数为( )
A.0或3或4 B.0或1或3 C.0或1或3或4 D.0或1或4
4.(2019秋?东台市期中)如图,点A、B、C在同一条直线上,点D在直线AB外,过这四个点中的任意3个,能画的圆有( )
A.1 个 B.2个 C.3个 D.4 个
5.(2018秋?兴化市月考)小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是( )
A.第一块 B.第二块 C.第三块 D.第四块
6.(2018?镇江模拟)如图,已知点平面直角坐标系内三点A(3,0)、B(5,0)、C(0,4),⊙P经过点A、B、C,则点P的坐标为( )
A.(6,8) B.(4,5) C.(4,318) D.(4,338)
7.(2020秋?海淀区期中)如图,不等边△ABC内接于⊙O,下列结论不成立的是( )
A.∠1=∠2 B.∠1=∠4 C.∠AOB=2∠ACB D.∠ACB=∠2+∠3
8.(2020?汶上县一模)如图,在直角坐标系中,点A(0,3)、点B(4,3)、点C(0,﹣1),则△ABC外接圆的半径为( )
A.2 B.3 C.4 D.22
9.(2020春?江州区期末)A、B、C分别表示三个村庄,AB=1700米,BC=800米,AC=1500米,某社区拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
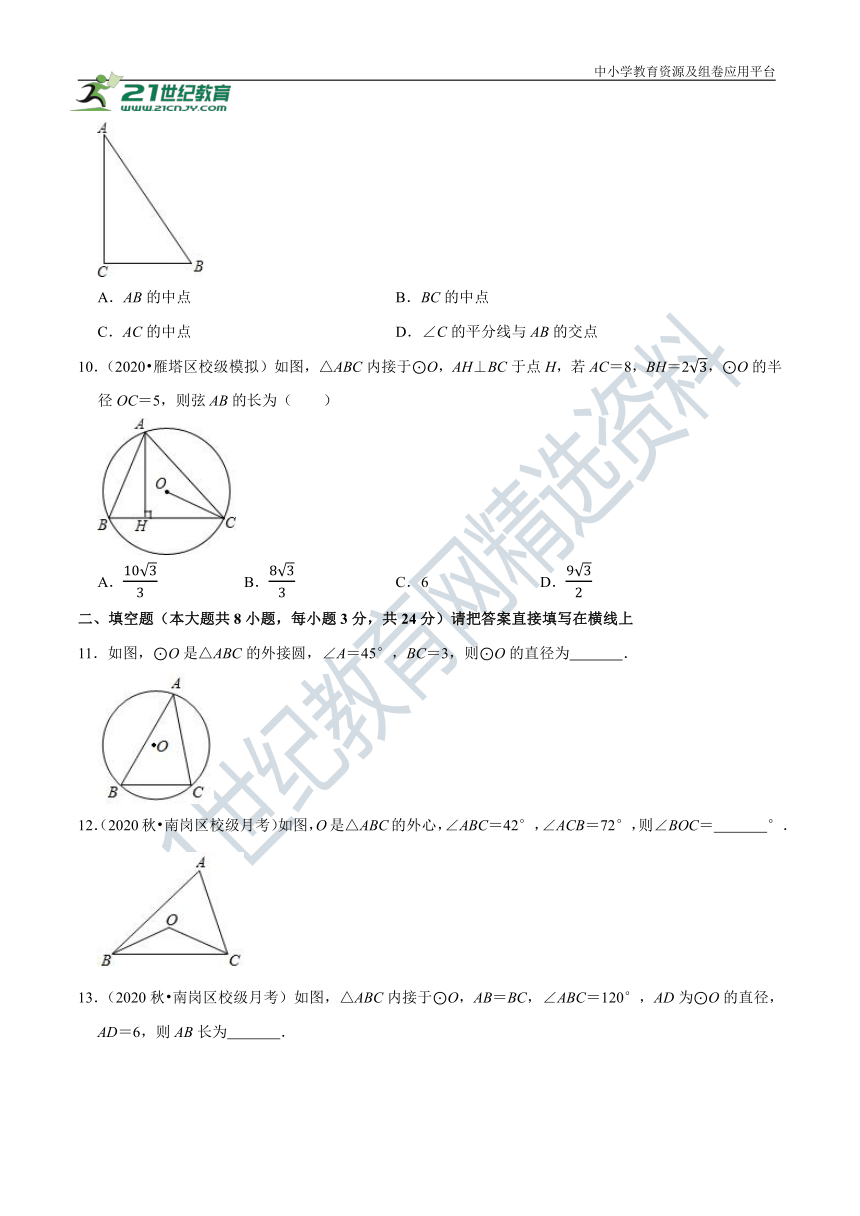
A.AB的中点 B.BC的中点
C.AC的中点 D.∠C的平分线与AB的交点
10.(2020?雁塔区校级模拟)如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=8,BH=23,⊙O的半径OC=5,则弦AB的长为( )
A.1033 B.833 C.6 D.932
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.如图,⊙O是△ABC的外接圆,∠A=45°,BC=3,则⊙O的直径为 .
12.(2020秋?南岗区校级月考)如图,O是△ABC的外心,∠ABC=42°,∠ACB=72°,则∠BOC= °.
13.(2020秋?南岗区校级月考)如图,△ABC内接于⊙O,AB=BC,∠ABC=120°,AD为⊙O的直径,AD=6,则AB长为 .
14.(2020?鼓楼区校级模拟)如图,⊙O是△ABC的外接圆,AB=4,∠B=30°,tanC=43,则⊙O的半径是 .
15.(2020?吉安模拟)△ABC内接于⊙O,∠B=70°,∠OCB=50°,点P是⊙O上一个动点(不与图中已知点重合),若△ACP是等腰三角形,则∠ACP的度数为 .
16.(2020春?越城区期中)如图,AB为△ADC的外接圆⊙O的直径,若∠BAD=50°,则∠ACD= °.
17.(2019秋?北京期末)如图,在平面直角坐标系中,点A,B,C都在格点上,过A,B,C三点作一圆弧,则圆心的坐标是 .
18.(2020?路北区二模)如图,已知⊙O的半径为2,△ABC内接于⊙O,∠ACB=135°,则AB= .弓形ACB的面积为 .
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020秋?秀洲区月考)将图中的破轮子复原,已知弧上三点A,B,C.
(1)画出该轮的圆心;
(2)若△ABC是等腰三角形,底边BC=16cm,腰AB=10cm,求圆片的半径R.
20.(2020?湖州)如图,已知△ABC是⊙O的内接三角形,AD是⊙O的直径,连结BD,BC平分∠ABD.
(1)求证:∠CAD=∠ABC;
(2)若AD=6,求CD的长.
21.(2020?鼓楼区一模)如图,△ABC内接于⊙O,∠BAC=45°,AD⊥BC,垂足为D,BD=6,DC=4.
(1)求⊙O的半径;
(2)求AD的长.
22.(2020?泰兴市一模)如图,△ABC是⊙O的内接三角形.AE是⊙O的直径,交BC于点G.过点A作AF⊥BC,AF分别与BC、⊙O交于点D、F,连接BE、CF.
(1)求证:∠BAE=∠CAF;
(2)若AB=8,AC=6,AG=5,求AF的长.
23.(2020?浙江自主招生)已知:如图,在△ABC中,∠BAC=30°,BC=4,求△ABC面积的最大值.
24.(2020?鹿城区校级二模)如图,Rt△ABC中,∠C=90°,M为AB上一点,过M,C,B三点的⊙O交AC于P,过点P作PD∥AB,交⊙O于点D.
(1)若M是AB中点,连结MD,求证:四边形APDM是平行四边形;
(2)连结PM,当PM=PC,且AC=4,tanA=12,求线段PD的长.
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解析】①过不在同一直线上的三点可以作一个圆,故原命题错误,符合题意;
②圆内接四边形对角互补,错误,符合题意;
③平分弦(不是直径)的直径垂直于弦,故原命题错误,符合题意;
④同圆或等圆中,相等的圆周角所对的弧也相等,故原命题错误,符合题意.
错误的有①②③④,
故选:D.
2.【解析】①同圆或等圆中,相等的圆心角所对的弧相等,故不符合题意;
②平分弦(弦不是直径)的直径垂直于弦;故不符合题意;
③圆是轴对称图形,任何一条直径所在直线都是它的对称轴;故符合题意;
④把这题一条直线上的三点确定一个圆,故不符合题意,
故选:A.
3.【解析】如图,当四点在同一条直线上时,不能确定圆,当四点共圆时,只能作一个圆,当三点在同一直线上时,可以作三个圆,当四点不共圆时,且没有三点共线时,能确定四个圆.
故选:C.
4.【解析】∵点A、B、C在同一条直线上,
∴经过点A、B、D,或点A、C、D,或点B、C、D分别能画一个圆,
故选:C.
5.【解析】第①块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
6.【解析】∵⊙P经过点A、B、C,
∴点P在线段AB的垂直平分线上,
∴点P的横坐标为4,
设点P的坐标为(4,y),
作PE⊥OB于E,PF⊥OC于F,
由题意得,
42+(y-4)2=12+y2,
解得,y=318,
故选:C.
7.【解析】∵OB=OC,
∴∠1=∠2,所以A选项的结论成立;
∵OA=OB,
∴∠4=∠OBA,
∴∠AOB=180°﹣∠4﹣∠OBA=180°﹣2∠4,
∵△ABC为不等边三角形,
∴AB≠BC,
∴∠BOC≠∠AOB,
而∠BOC=180°﹣∠1﹣∠2=180°﹣2∠1,
∴∠1≠∠4,所以B选项的结论不成立;
∵∠AOB与∠ACB都对AB,
∴∠AOB=2∠ACB,所以C选项的结论成立;
∵OA=OC,
∴∠OCA=∠3,
∴∠ACB=∠1+∠OCA=∠2+∠3,所以D选项的结论成立.
故选:B.
8.【解析】连接AB、BC,如图,
∵A(0,3)、B(4,3),
∴AB⊥y轴,
∴∠BAC=90°,
∴BC为△ABC外接圆的直径,
∵AC=3+1=4,AB=4,
∴BC=42+42=42,
∴△ABC外接圆的半径为22.
故选:D.
9【解析】∵AB=1700米,BC=800米,AC=1500米,
∴BC2+AC2=AB2,
∴∠C=90°,
根据直角三角形斜边上的中线等于斜边的一半得出活动中心P的位置应为斜边AB的中点,
故选:A.
10.【解析】如图,延长CO交⊙O于D,连接AD,
∵CD为⊙O的直径,
∴CD=2OC=10,∠DAC=90°,
∴AD=CD2-AC2=100-64=6,
∵∠DAC=∠BHA=90°,∠D=∠B,
∴△ADC∽△HBA,
∴BHAD=ABCD,
∴236=AB10,
∴AB=1033,
故选:A.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解析】连接OB、OC,如图,∵∠BOC=2∠A=90°,
而OB=OC,
∴△OBC为等腰直角三角形,
∴OB=22BC=322,
∴⊙O的直径为32.
故答案为32.
12.【解析】∵∠ABC=42°,∠ACB=72°,
∴∠BAC=180°﹣42°﹣72°=66°,
∵O是△ABC的外心,
∴以O为圆心,OB为半径的圆是△ABC的外接圆,
∴∠BOC=2∠BAC=132°.
故答案为132,
13.【解析】∵AB=BC,∠ABC=120°,
∴∠ACB=30°,
∴∠ADB=30°,
∵AD为⊙O的直径,
∴∠ABD=90°,
∴AB=12AD=12×6=3.
故答案为3.
14.【解析】作直径AD,连接BD,如图,
∵AD为直径,
∴∠ABD=90°,
∵∠D=∠C,
∴tanD=tanC=43,
在Rt△ABD中,tanD=ABBD=43,
而AB=4,
∴BD=3,
∴AD=32+42=5,
∴⊙O的半径为52.
故答案为52.
15.【解析】如图,连接OA,OB,
∵∠OCB=50°,
∴∠OBC=50°,
∵∠B=70°,
∴∠OBA=∠OAB=20°,
∴∠AOB=140°,
∴∠AOC=360°﹣80°﹣140°=140°,
∴∠OAC=∠OCA=20°,
∴∠ACB=50°+20°=70°,
∴AB=AC,
当AP′=AC时,
此时点P′与点B重合,不符合题意;
当AP=PC时,
∵∠B=70°,
∴∠APC=180°﹣70°=110°,
∴∠ACP=∠CAP=12(180°﹣110°)=35°;
当AP′=P′C时,
∠P′AC=∠P′CA=12(180°﹣70)=55°;
当AC=P′C时,
∠ACP′=180°﹣70°﹣70°=40°.
故答案为:35°或55°或40°.
16.【解析】如图,连接BD,
∵AB为△ADC的外接圆⊙O的直径,
∴∠ADB=90°,
∵∠BAD=50°,
∴∠ABD=90°﹣50°=40°,
∴∠ACD=∠ABD=40°.
故答案为:40.
17.【解析】根据垂径定理的推论:弦的垂直平分线必过圆心,
可以作弦AB和BC的垂直平分线,交点即为圆心.
如图所示,则圆心是(2,1).
故答案为:(2,1).
18.【解析】在优弧AB上取点D,连接AD、BD、OA、OB,
∵四边形ADBC为圆内接四边形,
∴∠D=180°﹣∠ACB=45°,
由圆周角定理得,∠AOB=2∠D=90°,
∵OA=OB,∠AOB=90°,
∴AB=2OA=22,
弓形ACB的面积=90π×22360-12×2×2=π﹣2,
故答案为:22;π﹣2.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解析】(1)如图所示:分别作弦AB和AC的垂直平分线交点O即为所求的圆心;
(2)连接AO,OB,
∵BC=16cm,
∴BD=8cm,
∵AB=10cm,
∴AD=6cm,
设圆片的半径为R,在Rt△BOD中,OD=(R﹣6)cm,
∴R2=82+(R﹣6)2,
解得:R=253cm,
∴圆片的半径R为253cm.
20.【解析】(1)∵BC平分∠ABD,
∴∠DBC=∠ABC,
∵∠CAD=∠DBC,
∴∠CAD=∠ABC;
(2)∵∠CAD=∠ABC,
∴CD=AC,
∵AD是⊙O的直径,AD=6,
∴CD的长=12×12×π×6=32π.
21.【解析】(1)如图1,连接OB、OC,
∵BD=6,DC=4,
∴BC=10,
由圆周角定理得,∠BOC=2∠BAC=90°,
∴OB=22BC=52;
(2)如图2,连接OA,过点O作OE⊥AD于E,OF⊥BC于F,
∴BF=FC=5,
∴DF=1,
∵∠BOC=90°,BF=FC,
∴OF=12BC=5,
∵AD⊥BC,OE⊥AD,OF⊥BC,
∴四边形OFDE为矩形,
∴OE=DF=1,DE=OF=5,
在Rt△AOE中,AE=OA2-OE2=7,
∴AD=AE+DE=12.
22.【解答】(1)证明:∵AF⊥BC,
∴∠ADC=90°,
∴∠ACB+∠CAF=90°,
∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠BAE+∠E=90°,
由圆周角定理得,∠ACB=∠E,
∴∠BAE=∠CAF;
(2)解:由圆周角定理得,∠ABG=∠AFC,又∠BAE=∠CAF,
∴△ABG∽△AFC,
∴ABAF=AGAC,即8AF=56,
解得,AF=485.
23.【解析】作出△ABC的外接圆⊙O,连接OB,OC,当△ABC的BC边上的高经过点O时,△ABC面积最大,
如图,过点O作OD⊥BC,并延长DO交圆于点A',连接A'B,A'C,
∵∠BAC=30°,
∴∠BOC=60°,
∵OB=OC,
∴△OBC为等边三角形,
∴∠BOD=30°,OB=OA'=BC=4,
∴OD=23,
∴A'D=4+23,
∴S△A'BC=12×BC×A'D=12×4×(4+23)=8+43.
24.【解答】(1)证明:连接CM,PB,DM,如图1所示:
∵∠C=90°,四边形BCPM为圆内接四边形,
∴∠C+∠BMP=180°,
∴∠BMP=90°,BP为⊙O的直径,
又∵PD∥AB,
∴∠DPM=180°﹣∠BMP=90°,
∴MD为⊙O的直径,
∵∠C=90°,M为AB的中点,
∴CM=12AB=BM,
∴CM=BM,
又∵MD为⊙O的直径,
∴DM垂直平分BC,
∴PC∥MD,
∴四边形APDM为平行四边形;
(2)解:连接BD、CD、BP,如图2所示:
∵MD和BP均为⊙O的直径,
∴∠DPM=∠PMB=∠PDB=90°,
∴四边形PDBM为矩形,
∴PM=BD,
∵PM=PC,
∴PC=BD,
在Rt△BPD和Rt△PBC中,BP=PBBD=PC,
∴Rt△BPD≌Rt△PBC(HL),
∴PD=BC,
在Rt△ACB中,AC=4,tanA=BCAC=12,
∴BC=4tanA=2,
∴PD=BC=2.
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,其中选择10道、填空6道、解答8道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2019秋?北仑区期末)下列四个结论,不正确的是( )
①过三点可以作一个圆;
②圆内接四边形对角相等;
③平分弦的直径垂直于弦;
④相等的圆周角所对的弧也相等.
A.②③ B.①③④ C.①②④ D.①②③④
2.(2020秋?崇川区校级月考)下列语句中正确的有( )
①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③圆的轴对称图形,任何一条直径所在直线都是它的对称轴;④三点确定一个圆.
A.1个 B.2个 C.3个 D.4个
3.(2019?吴兴区校级一模)平面上有四个点,过其中任意3个点一共能确定圆的个数为( )
A.0或3或4 B.0或1或3 C.0或1或3或4 D.0或1或4
4.(2019秋?东台市期中)如图,点A、B、C在同一条直线上,点D在直线AB外,过这四个点中的任意3个,能画的圆有( )
A.1 个 B.2个 C.3个 D.4 个
5.(2018秋?兴化市月考)小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是( )
A.第一块 B.第二块 C.第三块 D.第四块
6.(2018?镇江模拟)如图,已知点平面直角坐标系内三点A(3,0)、B(5,0)、C(0,4),⊙P经过点A、B、C,则点P的坐标为( )
A.(6,8) B.(4,5) C.(4,318) D.(4,338)
7.(2020秋?海淀区期中)如图,不等边△ABC内接于⊙O,下列结论不成立的是( )
A.∠1=∠2 B.∠1=∠4 C.∠AOB=2∠ACB D.∠ACB=∠2+∠3
8.(2020?汶上县一模)如图,在直角坐标系中,点A(0,3)、点B(4,3)、点C(0,﹣1),则△ABC外接圆的半径为( )
A.2 B.3 C.4 D.22
9.(2020春?江州区期末)A、B、C分别表示三个村庄,AB=1700米,BC=800米,AC=1500米,某社区拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
A.AB的中点 B.BC的中点
C.AC的中点 D.∠C的平分线与AB的交点
10.(2020?雁塔区校级模拟)如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=8,BH=23,⊙O的半径OC=5,则弦AB的长为( )
A.1033 B.833 C.6 D.932
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.如图,⊙O是△ABC的外接圆,∠A=45°,BC=3,则⊙O的直径为 .
12.(2020秋?南岗区校级月考)如图,O是△ABC的外心,∠ABC=42°,∠ACB=72°,则∠BOC= °.
13.(2020秋?南岗区校级月考)如图,△ABC内接于⊙O,AB=BC,∠ABC=120°,AD为⊙O的直径,AD=6,则AB长为 .
14.(2020?鼓楼区校级模拟)如图,⊙O是△ABC的外接圆,AB=4,∠B=30°,tanC=43,则⊙O的半径是 .
15.(2020?吉安模拟)△ABC内接于⊙O,∠B=70°,∠OCB=50°,点P是⊙O上一个动点(不与图中已知点重合),若△ACP是等腰三角形,则∠ACP的度数为 .
16.(2020春?越城区期中)如图,AB为△ADC的外接圆⊙O的直径,若∠BAD=50°,则∠ACD= °.
17.(2019秋?北京期末)如图,在平面直角坐标系中,点A,B,C都在格点上,过A,B,C三点作一圆弧,则圆心的坐标是 .
18.(2020?路北区二模)如图,已知⊙O的半径为2,△ABC内接于⊙O,∠ACB=135°,则AB= .弓形ACB的面积为 .
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020秋?秀洲区月考)将图中的破轮子复原,已知弧上三点A,B,C.
(1)画出该轮的圆心;
(2)若△ABC是等腰三角形,底边BC=16cm,腰AB=10cm,求圆片的半径R.
20.(2020?湖州)如图,已知△ABC是⊙O的内接三角形,AD是⊙O的直径,连结BD,BC平分∠ABD.
(1)求证:∠CAD=∠ABC;
(2)若AD=6,求CD的长.
21.(2020?鼓楼区一模)如图,△ABC内接于⊙O,∠BAC=45°,AD⊥BC,垂足为D,BD=6,DC=4.
(1)求⊙O的半径;
(2)求AD的长.
22.(2020?泰兴市一模)如图,△ABC是⊙O的内接三角形.AE是⊙O的直径,交BC于点G.过点A作AF⊥BC,AF分别与BC、⊙O交于点D、F,连接BE、CF.
(1)求证:∠BAE=∠CAF;
(2)若AB=8,AC=6,AG=5,求AF的长.
23.(2020?浙江自主招生)已知:如图,在△ABC中,∠BAC=30°,BC=4,求△ABC面积的最大值.
24.(2020?鹿城区校级二模)如图,Rt△ABC中,∠C=90°,M为AB上一点,过M,C,B三点的⊙O交AC于P,过点P作PD∥AB,交⊙O于点D.
(1)若M是AB中点,连结MD,求证:四边形APDM是平行四边形;
(2)连结PM,当PM=PC,且AC=4,tanA=12,求线段PD的长.
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解析】①过不在同一直线上的三点可以作一个圆,故原命题错误,符合题意;
②圆内接四边形对角互补,错误,符合题意;
③平分弦(不是直径)的直径垂直于弦,故原命题错误,符合题意;
④同圆或等圆中,相等的圆周角所对的弧也相等,故原命题错误,符合题意.
错误的有①②③④,
故选:D.
2.【解析】①同圆或等圆中,相等的圆心角所对的弧相等,故不符合题意;
②平分弦(弦不是直径)的直径垂直于弦;故不符合题意;
③圆是轴对称图形,任何一条直径所在直线都是它的对称轴;故符合题意;
④把这题一条直线上的三点确定一个圆,故不符合题意,
故选:A.
3.【解析】如图,当四点在同一条直线上时,不能确定圆,当四点共圆时,只能作一个圆,当三点在同一直线上时,可以作三个圆,当四点不共圆时,且没有三点共线时,能确定四个圆.
故选:C.
4.【解析】∵点A、B、C在同一条直线上,
∴经过点A、B、D,或点A、C、D,或点B、C、D分别能画一个圆,
故选:C.
5.【解析】第①块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
6.【解析】∵⊙P经过点A、B、C,
∴点P在线段AB的垂直平分线上,
∴点P的横坐标为4,
设点P的坐标为(4,y),
作PE⊥OB于E,PF⊥OC于F,
由题意得,
42+(y-4)2=12+y2,
解得,y=318,
故选:C.
7.【解析】∵OB=OC,
∴∠1=∠2,所以A选项的结论成立;
∵OA=OB,
∴∠4=∠OBA,
∴∠AOB=180°﹣∠4﹣∠OBA=180°﹣2∠4,
∵△ABC为不等边三角形,
∴AB≠BC,
∴∠BOC≠∠AOB,
而∠BOC=180°﹣∠1﹣∠2=180°﹣2∠1,
∴∠1≠∠4,所以B选项的结论不成立;
∵∠AOB与∠ACB都对AB,
∴∠AOB=2∠ACB,所以C选项的结论成立;
∵OA=OC,
∴∠OCA=∠3,
∴∠ACB=∠1+∠OCA=∠2+∠3,所以D选项的结论成立.
故选:B.
8.【解析】连接AB、BC,如图,
∵A(0,3)、B(4,3),
∴AB⊥y轴,
∴∠BAC=90°,
∴BC为△ABC外接圆的直径,
∵AC=3+1=4,AB=4,
∴BC=42+42=42,
∴△ABC外接圆的半径为22.
故选:D.
9【解析】∵AB=1700米,BC=800米,AC=1500米,
∴BC2+AC2=AB2,
∴∠C=90°,
根据直角三角形斜边上的中线等于斜边的一半得出活动中心P的位置应为斜边AB的中点,
故选:A.
10.【解析】如图,延长CO交⊙O于D,连接AD,
∵CD为⊙O的直径,
∴CD=2OC=10,∠DAC=90°,
∴AD=CD2-AC2=100-64=6,
∵∠DAC=∠BHA=90°,∠D=∠B,
∴△ADC∽△HBA,
∴BHAD=ABCD,
∴236=AB10,
∴AB=1033,
故选:A.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解析】连接OB、OC,如图,∵∠BOC=2∠A=90°,
而OB=OC,
∴△OBC为等腰直角三角形,
∴OB=22BC=322,
∴⊙O的直径为32.
故答案为32.
12.【解析】∵∠ABC=42°,∠ACB=72°,
∴∠BAC=180°﹣42°﹣72°=66°,
∵O是△ABC的外心,
∴以O为圆心,OB为半径的圆是△ABC的外接圆,
∴∠BOC=2∠BAC=132°.
故答案为132,
13.【解析】∵AB=BC,∠ABC=120°,
∴∠ACB=30°,
∴∠ADB=30°,
∵AD为⊙O的直径,
∴∠ABD=90°,
∴AB=12AD=12×6=3.
故答案为3.
14.【解析】作直径AD,连接BD,如图,
∵AD为直径,
∴∠ABD=90°,
∵∠D=∠C,
∴tanD=tanC=43,
在Rt△ABD中,tanD=ABBD=43,
而AB=4,
∴BD=3,
∴AD=32+42=5,
∴⊙O的半径为52.
故答案为52.
15.【解析】如图,连接OA,OB,
∵∠OCB=50°,
∴∠OBC=50°,
∵∠B=70°,
∴∠OBA=∠OAB=20°,
∴∠AOB=140°,
∴∠AOC=360°﹣80°﹣140°=140°,
∴∠OAC=∠OCA=20°,
∴∠ACB=50°+20°=70°,
∴AB=AC,
当AP′=AC时,
此时点P′与点B重合,不符合题意;
当AP=PC时,
∵∠B=70°,
∴∠APC=180°﹣70°=110°,
∴∠ACP=∠CAP=12(180°﹣110°)=35°;
当AP′=P′C时,
∠P′AC=∠P′CA=12(180°﹣70)=55°;
当AC=P′C时,
∠ACP′=180°﹣70°﹣70°=40°.
故答案为:35°或55°或40°.
16.【解析】如图,连接BD,
∵AB为△ADC的外接圆⊙O的直径,
∴∠ADB=90°,
∵∠BAD=50°,
∴∠ABD=90°﹣50°=40°,
∴∠ACD=∠ABD=40°.
故答案为:40.
17.【解析】根据垂径定理的推论:弦的垂直平分线必过圆心,
可以作弦AB和BC的垂直平分线,交点即为圆心.
如图所示,则圆心是(2,1).
故答案为:(2,1).
18.【解析】在优弧AB上取点D,连接AD、BD、OA、OB,
∵四边形ADBC为圆内接四边形,
∴∠D=180°﹣∠ACB=45°,
由圆周角定理得,∠AOB=2∠D=90°,
∵OA=OB,∠AOB=90°,
∴AB=2OA=22,
弓形ACB的面积=90π×22360-12×2×2=π﹣2,
故答案为:22;π﹣2.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解析】(1)如图所示:分别作弦AB和AC的垂直平分线交点O即为所求的圆心;
(2)连接AO,OB,
∵BC=16cm,
∴BD=8cm,
∵AB=10cm,
∴AD=6cm,
设圆片的半径为R,在Rt△BOD中,OD=(R﹣6)cm,
∴R2=82+(R﹣6)2,
解得:R=253cm,
∴圆片的半径R为253cm.
20.【解析】(1)∵BC平分∠ABD,
∴∠DBC=∠ABC,
∵∠CAD=∠DBC,
∴∠CAD=∠ABC;
(2)∵∠CAD=∠ABC,
∴CD=AC,
∵AD是⊙O的直径,AD=6,
∴CD的长=12×12×π×6=32π.
21.【解析】(1)如图1,连接OB、OC,
∵BD=6,DC=4,
∴BC=10,
由圆周角定理得,∠BOC=2∠BAC=90°,
∴OB=22BC=52;
(2)如图2,连接OA,过点O作OE⊥AD于E,OF⊥BC于F,
∴BF=FC=5,
∴DF=1,
∵∠BOC=90°,BF=FC,
∴OF=12BC=5,
∵AD⊥BC,OE⊥AD,OF⊥BC,
∴四边形OFDE为矩形,
∴OE=DF=1,DE=OF=5,
在Rt△AOE中,AE=OA2-OE2=7,
∴AD=AE+DE=12.
22.【解答】(1)证明:∵AF⊥BC,
∴∠ADC=90°,
∴∠ACB+∠CAF=90°,
∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠BAE+∠E=90°,
由圆周角定理得,∠ACB=∠E,
∴∠BAE=∠CAF;
(2)解:由圆周角定理得,∠ABG=∠AFC,又∠BAE=∠CAF,
∴△ABG∽△AFC,
∴ABAF=AGAC,即8AF=56,
解得,AF=485.
23.【解析】作出△ABC的外接圆⊙O,连接OB,OC,当△ABC的BC边上的高经过点O时,△ABC面积最大,
如图,过点O作OD⊥BC,并延长DO交圆于点A',连接A'B,A'C,
∵∠BAC=30°,
∴∠BOC=60°,
∵OB=OC,
∴△OBC为等边三角形,
∴∠BOD=30°,OB=OA'=BC=4,
∴OD=23,
∴A'D=4+23,
∴S△A'BC=12×BC×A'D=12×4×(4+23)=8+43.
24.【解答】(1)证明:连接CM,PB,DM,如图1所示:
∵∠C=90°,四边形BCPM为圆内接四边形,
∴∠C+∠BMP=180°,
∴∠BMP=90°,BP为⊙O的直径,
又∵PD∥AB,
∴∠DPM=180°﹣∠BMP=90°,
∴MD为⊙O的直径,
∵∠C=90°,M为AB的中点,
∴CM=12AB=BM,
∴CM=BM,
又∵MD为⊙O的直径,
∴DM垂直平分BC,
∴PC∥MD,
∴四边形APDM为平行四边形;
(2)解:连接BD、CD、BP,如图2所示:
∵MD和BP均为⊙O的直径,
∴∠DPM=∠PMB=∠PDB=90°,
∴四边形PDBM为矩形,
∴PM=BD,
∵PM=PC,
∴PC=BD,
在Rt△BPD和Rt△PBC中,BP=PBBD=PC,
∴Rt△BPD≌Rt△PBC(HL),
∴PD=BC,
在Rt△ACB中,AC=4,tanA=BCAC=12,
∴BC=4tanA=2,
∴PD=BC=2.
