3.8 圆内接正多边形同步练习(含解析)
文档属性
| 名称 | 3.8 圆内接正多边形同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 10:24:57 | ||
图片预览



文档简介
3.9圆内接正多边形
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,其中选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2019秋?东丽区期末)边长为2的正六边形的面积为( )
A.63 B.62 C.6 D.3
2.(2020?番禺区模拟)如图,四边形ABCD是⊙O的内接正方形,点P是CD上不同于点C的任意一点,则∠BPC的大小是( )
A.22.5° B.45° C.30° D.50°
3.(2020?保定模拟)如图,△ABD是⊙O的内接正三角形,四边形ACEF是⊙O的内接正四边形,若线段BC恰是⊙O的一个内接正n边形的一条边,则n=( )
A.16 B.12 C.10 D.8
4.(2020?南充模拟)如图,把边长相等的正六边形ABCDEF和正五边形ABGHI的AB边重合叠放在一起,连接EB,交HI于点K,则∠BKI的大小为( )
A.90° B.85° C.84° D.80°
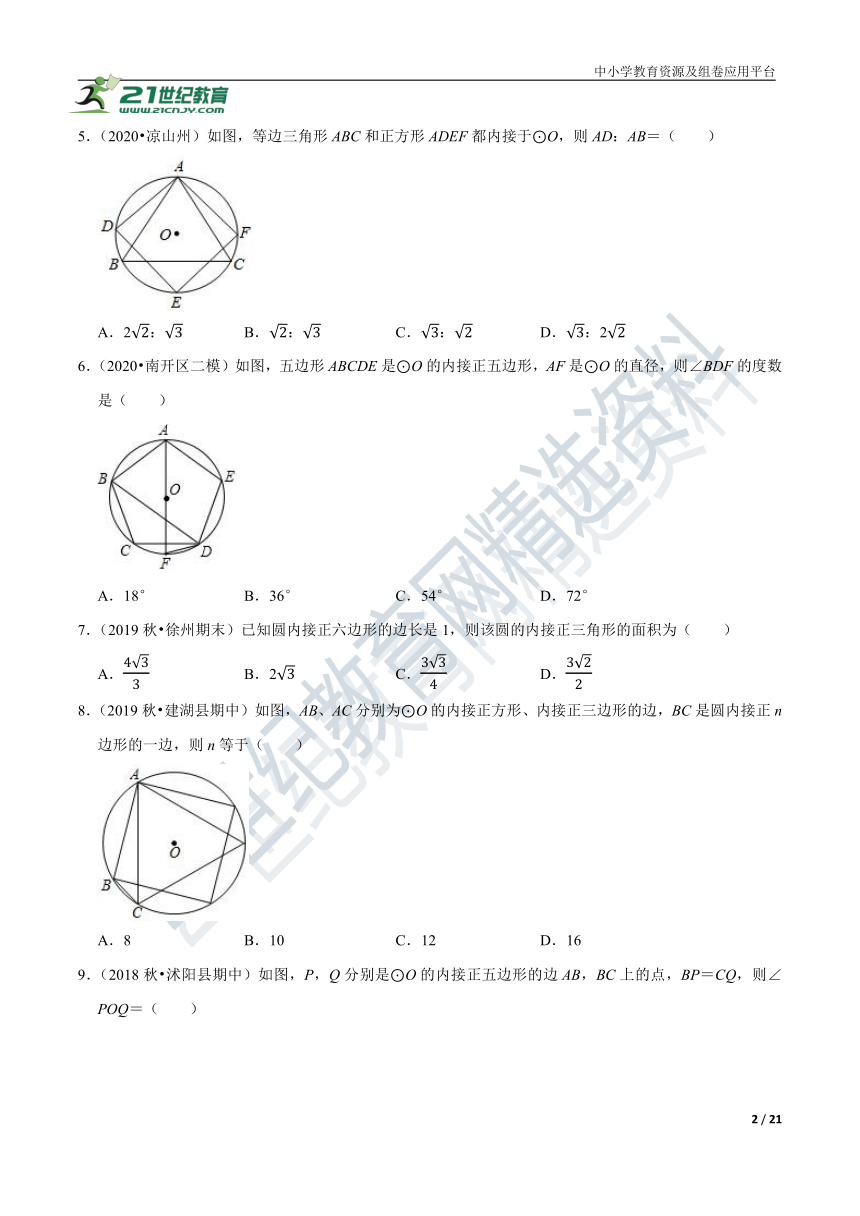
5.(2020?凉山州)如图,等边三角形ABC和正方形ADEF都内接于⊙O,则AD:AB=( )
A.22:3 B.2:3 C.3:2 D.3:22
6.(2020?南开区二模)如图,五边形ABCDE是⊙O的内接正五边形,AF是⊙O的直径,则∠BDF的度数是( )
A.18° B.36° C.54° D.72°
7.(2019秋?徐州期末)已知圆内接正六边形的边长是1,则该圆的内接正三角形的面积为( )
A.433 B.23 C.334 D.322
8.(2019秋?建湖县期中)如图,AB、AC分别为⊙O的内接正方形、内接正三边形的边,BC是圆内接正n边形的一边,则n等于( )
A.8 B.10 C.12 D.16
9.(2018秋?沭阳县期中)如图,P,Q分别是⊙O的内接正五边形的边AB,BC上的点,BP=CQ,则∠POQ=( )
A.75° B.54° C.72° D.60°
10.(2019秋?莱山区期末)如图,AB,AC分别为⊙O的内接正三角形和内接正四边形的一边,若BC恰好是同圆的一个内接正n边形的一边,则n的值为( )
A.8 B.10 C.12 D.15
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020?历下区二模)正方形的边长为6,则该正方形的边心距是 .
12.(2020?雁塔区校级二模)如图,在正六边形ABCDEF中,连接BD、BE、DF,则BEDF的值为 .
13.已知正五边形ABCDE内接于⊙O,连接BD,则∠ABD的度数是 .
14.(2019秋?东城区校级期中)如图,正六边形ABCDEF内接于⊙O且半径为3,则AB的长为 .
15.(2019秋?惠民县期中)如图,正六边形ABCDEF内接于⊙O,若⊙O的半径为2,则△ADE的周长是 .
16.(2019秋?鼓楼区期中)如图,AB是⊙O的内接正方形一边,点C在弧AB上,且AC是⊙O的内接正六边形的一边,若将BC看作是⊙O的内接正n边形的一边,则n的值是 .
17.(2019秋?镇江期末)如图,⊙O半径为2,正方形ABCD内接于⊙O,点E在ADC上运动,连接BE,作AF⊥BE,垂足为F,连接CF.则CF长的最小值为 .
18.(2014?余姚市校级自主招生)已知:圆内接正方形ABCD,∠DAC的平分线交圆于E,交CD于P,若EP=1,AP=3,则圆的半径r= .
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
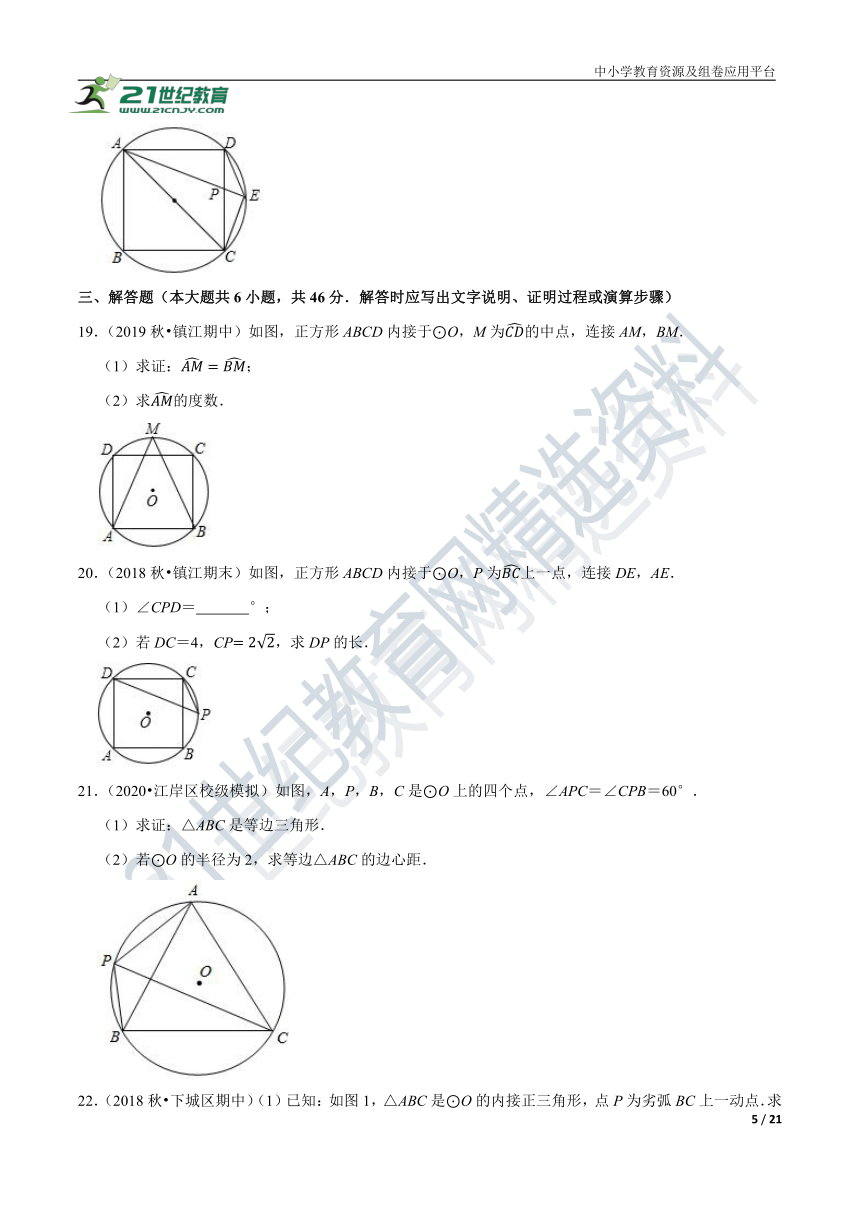
19.(2019秋?镇江期中)如图,正方形ABCD内接于⊙O,M为CD的中点,连接AM,BM.
(1)求证:AM=BM;
(2)求AM的度数.
20.(2018秋?镇江期末)如图,正方形ABCD内接于⊙O,P为BC上一点,连接DE,AE.
(1)∠CPD= °;
(2)若DC=4,CP=22,求DP的长.
21.(2020?江岸区校级模拟)如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形.
(2)若⊙O的半径为2,求等边△ABC的边心距.
22.(2018秋?下城区期中)(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为劣弧BC上一动点.求证:PA=PB+PC;
(2)已知:如图2,四边形ABCD是⊙O的内接正方形,点P为劣弧BC上一动点.求证:PA=PC+2PB.
23.(2017秋?青山区期中)如图正方形ABCD内接于⊙O,E为CD任意一点,连接DE、AE.
(1)求∠AED的度数.
(2)如图2,过点B作BF∥DE交⊙O于点F,连接AF,AF=1,AE=4,求DE的长度.
24.(2018秋?大连月考)如图1,△ABC为等边三角形,图2为正方形,图3为正五边形,图4为正多边形.
(1)如图1当BP=CQ时,请求出∠AOQ的度数,并说明理由
(2)如图2,在正方形中,当BP=CQ时∠AOQ= ;如图3,在正五边形中,当BP=CQ时,∠AOQ= ;
(3)如图4,在正n边形中,当BP=CQ时,∠AOQ是否有什么规律?如果有请用含有n的式子直接表示;如果没有规律,请说明理由.
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解析】如图,连接OB,OC,过点O作OH⊥BC于H,
∵六边形ABCDEF是正六边形,
∴∠BOC=16×360°=60°,
∵OB=0C,
∴△OBC是等边三角形,
∴BC=OB=OC=2,
∴它的半径为2,边长为2;
∵在Rt△OBH中,OH=OB?sin60°=2×32,
∴边心距是:3;
∴S正六边形ABCDEF=6S△OBC=6×12×2×3=63.
故选:A.
2.【解析】如图,连接OB、OC,则∠BOC=90°,
根据圆周角定理,得:∠BPC=12∠BOC=45°.
故选:B.
3.【解析】连接OA、OB、OC,如图,
∵AB,AC分别为⊙O的内接正四边形与内接正三角形的一边,
∴∠AOC=360°4=90°,∠AOB=360°3=120°,
∴∠BOC=∠AOB﹣∠AOC=30°,
∴n=360°30°=12,
即BC恰好是同圆内接一个正十二边形的一边.
故选:B.
4.【解析】由正五边形内角,得
∠I=∠BAI=(5-2)×180°5=108°,
由正六边形内角,得
∠ABC=(6-2)×180°6=120°,
∵BE平分∠ABC,
∴∠ABK=60°,
∴由四边形的内角和,得
∠BKI=360°﹣∠I﹣∠BAI﹣∠ABK
=360°﹣108°﹣108°﹣60°
=84°.
故选:C.
5.【解析】连接OA、OB、OD,过O作OH⊥AB于H,如图所示:
则AH=BH=12AB,
∵等边三角形ABC和正方形ADEF,都内接于⊙O,
∴∠AOB=120°,∠AOD=90°,
∵OA=OD=OB,
∴△AOD是等腰直角三角形,∠AOH=∠BOH=12×120°=60°,
∴AD=2OA,AH=OA?sin60°=32OA,
∴AB=2AH=2×32OA=3OA,
∴ADAB=2OA3OA=23,
故选:B.
6.【解析】∵AF是⊙O的直径,五边形ABCDE是⊙O的内接正五边形,
∴CF=DF,BC=DE,∠BAE=108°,
∴BF=EF,
∴∠BAF=12∠BAE=54°,
∴∠BDF=∠BAF=54°,
故选:C.
7.【解析】如图(二),
∵圆内接正六边形边长为1,
∴AB=1,
可得△OAB是等边三角形,圆的半径为1,
∴如图(一),
连接OB,过O作OD⊥BC于D,
则∠OBC=30°,BD=OB?cos30°=32×1=32,
故BC=2BD=3.OD=12OB=12,
∴圆的内接正三角形的面积=12×3×32=334,
故选:C.
8.【解析】连接AO,BO,CO.
∵AB、AC分别为⊙O的内接正方形、内接正三边形的一边,
∴∠AOB=360°4=90°,∠AOC=360°3=120°,
∴∠BOC=30°,
∴n=360°30°=12,
故选:C.
9.【解析】连接OA、OB、OC,
∵五边形ABCDE是⊙O的内接正五边形,
∴∠AOB=∠BOC=72°,
∵OA=OB,OB=OC,
∴∠OBA=∠OCB=54°,
在△OBP和△OCQ中,OB=OC∠OBP=∠OCQBP=CQ,
∴△OBP≌△OCQ,(SAS),
∴∠BOP=∠COQ,
∵∠AOB=∠AOP+∠BOP,∠BOC=∠BOQ+∠QOC,
∴∠BOP=∠QOC,
∵∠POQ=∠BOP+∠BOQ,∠BOC=∠BOQ+∠QOC,
∴∠POQ=∠BOC=72°.
故选:C.
10.【解析】连接OA、OB、OC,如图,
∵AB,AC分别为⊙O的内接正四边形与内接正三角形的一边,
∴∠AOC=360°4=90°,∠AOB=360°3=120°,
∴∠BOC=∠AOB﹣∠AOC=30°,
∴n=360°30°=12,
即BC恰好是同圆内接一个正十二边形的一边.
故选:C.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解析】如图所示:作OE⊥BC,
∵四边形ABCD是⊙O的内接正方形,
∴∠OBE=45°,而OE⊥BC,
∴BE=CE,
∴EB=OE=3,
故其边心距为3.
故答案为:3.
12.【解析】∵六边形ABCDEF是正六边形,
∴BC=CD=DE=EF,∠C=∠CDE=∠DEF=16(6﹣2)×180°=120°,
∴∠CDB=∠CBD=30°,
∴∠BDE=120°﹣30°=90°,∠DEB=∠FEB=60°,
∴∠DBE=30°,
∴BE=2DE,BD=3DE,
在△BCD和△DEF中,BC=DE∠C=∠DEFCD=EF,
∴△BCD≌△DEF(SAS),
∴BD=DF=3DE,
∴BEDF=2DE3DE=233;
故答案为:233.
13.【解析】∵五边形ABCDE为正五边形,
∴∠ABC=∠C=(5-2)×180°5=108°,
∵CD=CB,
∴∠CBD=180°-108°2=36°,
∴∠ABD=∠ABC﹣∠CBD=72°,
故答案为:72°.
14.【解析】连接OA、OB,如图所示:
∵正六边形ABCDEF内接于⊙O,
∴∠AOB=360°6=60°,
∵OA=OB=3,
∴△AOB是等边三角形,
∴AB=OA=OB=3,
故答案为:3.
15.【解析】连接OE,
∵多边形ABCDEF是正多边形,
∴∠DOE=360°6=60°,
∴∠DAE=12∠DOE=12×60°=30°,∠AED=90°,
∵⊙O的半径为2,
∴AD=2OD=4,
∴DE=12AD=12×2=1,AE=3DE=23,
∴△ADE的周长为2+4+23=6+23,
故答案为:6+23.
16.【解析】连接OC,
∵AB是⊙O内接正方形的一边,
∴∠AOB=360°÷4=90°,
∵BC是⊙O内接正六边形的一边,
∴∠AOC=360°÷6=60°,
∴∠BOC=∠AOB﹣∠AOC=90°﹣60°=30°,
∴n=360°÷30°=12;
故答案为:12;
17.【解析】如图,取AB的中点K,以AB为直径作⊙K,
∵AF⊥BE,
∴∠AFB=90°,
∵AK=BK,
∴KF=AK=BK,
∵正方形ABCD的外接圆的半径为2,
∴AB=BC=2?2=2,
∴KF=AK=KB=1,
∵∠CBK=90°,
∴CK=BK2+BC2=22+12=5,
∵CF≥CK﹣KF,
∴CF≥5-1,
∴CF的最小值为5-1.
故答案为5-1.
18.【解析】∵∠DAC的平分线交圆于E,
∴∠DAE=∠CAE,
∵∠CDE=∠CAE,
∴∠DAE=∠CDE,
∵∠AED=∠DEP,
∴△ADE∽△DPE,
∴PEDE=AEDE,
∴DE2=AE?EP;
∵EP=1,AP=3,
∴AE=4,
∴DE2=AE?EP=4,
∴DE=2
∵∠DAE=∠CAE,
∴弧DE=弧CE,
∴CE=DE=2,
∵圆内接正方形ABCD,
∴∠ADC=90,
∴AC是直径,
∴∠AEC=90,
∴AC=AE2+CE2=25,
∴r=5,
故答案为:5.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解答】(1)证明:∵四边形ABCD是正方形,
∴AD=BC,
∴AD=BC,
∵M为CD的中点,
∴DM=CM,
∴AD+DM=BC+CM,
∴AM=BM;
(2)解:连接OM,OA,OB,
∵正方形ABCD内接于⊙O,
∴∠AOB=90°,
∴∠AOM=∠BOM=12(360°﹣90°)=135°,
∴AM的度数时135°.
20.【解析】(1)如图,连接BD,
∵正方形ABCD内接于⊙O,P为BC上一点,
∴∠DBC=45°,
∵∠CPD=∠DBC,
∴∠CPD=45°.
故答案为:45;
(2)如图,作CH⊥DP于H,
∵CP=22,∠CPD=45°,
∴CH=PH=2,
∵DC=4,
∴DH=CD2-CH2=42-22=23,
∴DP=PH+DH=2+23.
21.【解答】(1)证明:在⊙O中,
∵∠BAC与∠CPB是BC对的圆周角,∠ABC与∠APC是AC所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
(2)过O作OD⊥BC于D,连接OB,
则∠OBD=30°,∠ODB=90°,
∵OB=2,
∴OD=1,
∴等边△ABC的边心距为1.
22.【解答】证明:(1)延长BP至E,使PE=PC,连接CE,如图1,
∵A、B、P、C四点共圆,
∴∠BAC+∠BPC=180°,
∵∠BPC+∠EPC=180°,
∴∠BAC=∠CPE=60°,
∵PE=PC,
∴△PCE是等边三角形,
∴CE=PC,∠E=60°;
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
∴∠BCE=∠ACP,
∵△ABC、△ECP为等边三角形,
∴CE=PC,AC=BC,
在△BEC和△APC中,
CE=PC∠BCE=∠ACPBC=AC,
∴△BEC≌△APC(SAS),
∴PA=BE=PB+PC;
(2)过点B作BE⊥PB交PA于E,连接OA,OB.如图2,
∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
∵∠APB=12∠AOB=45°,
∴BP=BE,
∴PE=2PB,
在△ABE和△CBP中,
BE=BP∠1=∠3AB=BC,
∴△ABE≌△CBP(SAS),
∴PC=AE,
∴PA=AE+PE=PC+2PB;
23.【解析】(1)如图1中,连接OA、OD.
∵四边形ABCD是正方形,
∴∠AOD=90°,
∴∠AED=12∠AOD=45°.
(2)如图2中,连接CF,CE,CA,BD,作DH⊥AE于H.
∵BF∥DE,AB∥CD,
∴∠BDE=∠DBF,∠BDC=∠ABD,
∴∠ABF=∠CDE,
∵∠CFA=∠AEC=90°,
∴∠DEC=∠AFB=135°,
∵CD=AB,
∴△CDE≌△ABF,
∴AF=CE=1,
∴AC=AE2+CE2=17,
∴AD=22AC=342,
∵∠DHE=90°,
∴∠HDE=∠HED=45°,
∴DH=HE,设DH=EH=x,
在Rt△ADH中,∵AD2=AH2+DH2,
∴344=(4﹣x)2+x2,
解得x=32或52(舍弃),
∴DE=2DH=322
24.【解析】(1)∠AOQ=60°.
在△ABP和△BCQ中,AB=BC∠ABC=∠CPB=CQ.
∴△ABP≌△BCQ(SAS).
∴∠BAP=∠CBQ.
∴∠AOQ=∠ABO+∠BAP=∠ABO+∠CBQ=∠ABC=60°;
(2)理由同(1):正方形∠AOQ=90°,正五边形∠AOQ=108°,
(3)正n边形∠AOQ=180°(n-2)n.
故答案为:90°,108°.
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,其中选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2019秋?东丽区期末)边长为2的正六边形的面积为( )
A.63 B.62 C.6 D.3
2.(2020?番禺区模拟)如图,四边形ABCD是⊙O的内接正方形,点P是CD上不同于点C的任意一点,则∠BPC的大小是( )
A.22.5° B.45° C.30° D.50°
3.(2020?保定模拟)如图,△ABD是⊙O的内接正三角形,四边形ACEF是⊙O的内接正四边形,若线段BC恰是⊙O的一个内接正n边形的一条边,则n=( )
A.16 B.12 C.10 D.8
4.(2020?南充模拟)如图,把边长相等的正六边形ABCDEF和正五边形ABGHI的AB边重合叠放在一起,连接EB,交HI于点K,则∠BKI的大小为( )
A.90° B.85° C.84° D.80°
5.(2020?凉山州)如图,等边三角形ABC和正方形ADEF都内接于⊙O,则AD:AB=( )
A.22:3 B.2:3 C.3:2 D.3:22
6.(2020?南开区二模)如图,五边形ABCDE是⊙O的内接正五边形,AF是⊙O的直径,则∠BDF的度数是( )
A.18° B.36° C.54° D.72°
7.(2019秋?徐州期末)已知圆内接正六边形的边长是1,则该圆的内接正三角形的面积为( )
A.433 B.23 C.334 D.322
8.(2019秋?建湖县期中)如图,AB、AC分别为⊙O的内接正方形、内接正三边形的边,BC是圆内接正n边形的一边,则n等于( )
A.8 B.10 C.12 D.16
9.(2018秋?沭阳县期中)如图,P,Q分别是⊙O的内接正五边形的边AB,BC上的点,BP=CQ,则∠POQ=( )
A.75° B.54° C.72° D.60°
10.(2019秋?莱山区期末)如图,AB,AC分别为⊙O的内接正三角形和内接正四边形的一边,若BC恰好是同圆的一个内接正n边形的一边,则n的值为( )
A.8 B.10 C.12 D.15
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020?历下区二模)正方形的边长为6,则该正方形的边心距是 .
12.(2020?雁塔区校级二模)如图,在正六边形ABCDEF中,连接BD、BE、DF,则BEDF的值为 .
13.已知正五边形ABCDE内接于⊙O,连接BD,则∠ABD的度数是 .
14.(2019秋?东城区校级期中)如图,正六边形ABCDEF内接于⊙O且半径为3,则AB的长为 .
15.(2019秋?惠民县期中)如图,正六边形ABCDEF内接于⊙O,若⊙O的半径为2,则△ADE的周长是 .
16.(2019秋?鼓楼区期中)如图,AB是⊙O的内接正方形一边,点C在弧AB上,且AC是⊙O的内接正六边形的一边,若将BC看作是⊙O的内接正n边形的一边,则n的值是 .
17.(2019秋?镇江期末)如图,⊙O半径为2,正方形ABCD内接于⊙O,点E在ADC上运动,连接BE,作AF⊥BE,垂足为F,连接CF.则CF长的最小值为 .
18.(2014?余姚市校级自主招生)已知:圆内接正方形ABCD,∠DAC的平分线交圆于E,交CD于P,若EP=1,AP=3,则圆的半径r= .
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2019秋?镇江期中)如图,正方形ABCD内接于⊙O,M为CD的中点,连接AM,BM.
(1)求证:AM=BM;
(2)求AM的度数.
20.(2018秋?镇江期末)如图,正方形ABCD内接于⊙O,P为BC上一点,连接DE,AE.
(1)∠CPD= °;
(2)若DC=4,CP=22,求DP的长.
21.(2020?江岸区校级模拟)如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形.
(2)若⊙O的半径为2,求等边△ABC的边心距.
22.(2018秋?下城区期中)(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为劣弧BC上一动点.求证:PA=PB+PC;
(2)已知:如图2,四边形ABCD是⊙O的内接正方形,点P为劣弧BC上一动点.求证:PA=PC+2PB.
23.(2017秋?青山区期中)如图正方形ABCD内接于⊙O,E为CD任意一点,连接DE、AE.
(1)求∠AED的度数.
(2)如图2,过点B作BF∥DE交⊙O于点F,连接AF,AF=1,AE=4,求DE的长度.
24.(2018秋?大连月考)如图1,△ABC为等边三角形,图2为正方形,图3为正五边形,图4为正多边形.
(1)如图1当BP=CQ时,请求出∠AOQ的度数,并说明理由
(2)如图2,在正方形中,当BP=CQ时∠AOQ= ;如图3,在正五边形中,当BP=CQ时,∠AOQ= ;
(3)如图4,在正n边形中,当BP=CQ时,∠AOQ是否有什么规律?如果有请用含有n的式子直接表示;如果没有规律,请说明理由.
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解析】如图,连接OB,OC,过点O作OH⊥BC于H,
∵六边形ABCDEF是正六边形,
∴∠BOC=16×360°=60°,
∵OB=0C,
∴△OBC是等边三角形,
∴BC=OB=OC=2,
∴它的半径为2,边长为2;
∵在Rt△OBH中,OH=OB?sin60°=2×32,
∴边心距是:3;
∴S正六边形ABCDEF=6S△OBC=6×12×2×3=63.
故选:A.
2.【解析】如图,连接OB、OC,则∠BOC=90°,
根据圆周角定理,得:∠BPC=12∠BOC=45°.
故选:B.
3.【解析】连接OA、OB、OC,如图,
∵AB,AC分别为⊙O的内接正四边形与内接正三角形的一边,
∴∠AOC=360°4=90°,∠AOB=360°3=120°,
∴∠BOC=∠AOB﹣∠AOC=30°,
∴n=360°30°=12,
即BC恰好是同圆内接一个正十二边形的一边.
故选:B.
4.【解析】由正五边形内角,得
∠I=∠BAI=(5-2)×180°5=108°,
由正六边形内角,得
∠ABC=(6-2)×180°6=120°,
∵BE平分∠ABC,
∴∠ABK=60°,
∴由四边形的内角和,得
∠BKI=360°﹣∠I﹣∠BAI﹣∠ABK
=360°﹣108°﹣108°﹣60°
=84°.
故选:C.
5.【解析】连接OA、OB、OD,过O作OH⊥AB于H,如图所示:
则AH=BH=12AB,
∵等边三角形ABC和正方形ADEF,都内接于⊙O,
∴∠AOB=120°,∠AOD=90°,
∵OA=OD=OB,
∴△AOD是等腰直角三角形,∠AOH=∠BOH=12×120°=60°,
∴AD=2OA,AH=OA?sin60°=32OA,
∴AB=2AH=2×32OA=3OA,
∴ADAB=2OA3OA=23,
故选:B.
6.【解析】∵AF是⊙O的直径,五边形ABCDE是⊙O的内接正五边形,
∴CF=DF,BC=DE,∠BAE=108°,
∴BF=EF,
∴∠BAF=12∠BAE=54°,
∴∠BDF=∠BAF=54°,
故选:C.
7.【解析】如图(二),
∵圆内接正六边形边长为1,
∴AB=1,
可得△OAB是等边三角形,圆的半径为1,
∴如图(一),
连接OB,过O作OD⊥BC于D,
则∠OBC=30°,BD=OB?cos30°=32×1=32,
故BC=2BD=3.OD=12OB=12,
∴圆的内接正三角形的面积=12×3×32=334,
故选:C.
8.【解析】连接AO,BO,CO.
∵AB、AC分别为⊙O的内接正方形、内接正三边形的一边,
∴∠AOB=360°4=90°,∠AOC=360°3=120°,
∴∠BOC=30°,
∴n=360°30°=12,
故选:C.
9.【解析】连接OA、OB、OC,
∵五边形ABCDE是⊙O的内接正五边形,
∴∠AOB=∠BOC=72°,
∵OA=OB,OB=OC,
∴∠OBA=∠OCB=54°,
在△OBP和△OCQ中,OB=OC∠OBP=∠OCQBP=CQ,
∴△OBP≌△OCQ,(SAS),
∴∠BOP=∠COQ,
∵∠AOB=∠AOP+∠BOP,∠BOC=∠BOQ+∠QOC,
∴∠BOP=∠QOC,
∵∠POQ=∠BOP+∠BOQ,∠BOC=∠BOQ+∠QOC,
∴∠POQ=∠BOC=72°.
故选:C.
10.【解析】连接OA、OB、OC,如图,
∵AB,AC分别为⊙O的内接正四边形与内接正三角形的一边,
∴∠AOC=360°4=90°,∠AOB=360°3=120°,
∴∠BOC=∠AOB﹣∠AOC=30°,
∴n=360°30°=12,
即BC恰好是同圆内接一个正十二边形的一边.
故选:C.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解析】如图所示:作OE⊥BC,
∵四边形ABCD是⊙O的内接正方形,
∴∠OBE=45°,而OE⊥BC,
∴BE=CE,
∴EB=OE=3,
故其边心距为3.
故答案为:3.
12.【解析】∵六边形ABCDEF是正六边形,
∴BC=CD=DE=EF,∠C=∠CDE=∠DEF=16(6﹣2)×180°=120°,
∴∠CDB=∠CBD=30°,
∴∠BDE=120°﹣30°=90°,∠DEB=∠FEB=60°,
∴∠DBE=30°,
∴BE=2DE,BD=3DE,
在△BCD和△DEF中,BC=DE∠C=∠DEFCD=EF,
∴△BCD≌△DEF(SAS),
∴BD=DF=3DE,
∴BEDF=2DE3DE=233;
故答案为:233.
13.【解析】∵五边形ABCDE为正五边形,
∴∠ABC=∠C=(5-2)×180°5=108°,
∵CD=CB,
∴∠CBD=180°-108°2=36°,
∴∠ABD=∠ABC﹣∠CBD=72°,
故答案为:72°.
14.【解析】连接OA、OB,如图所示:
∵正六边形ABCDEF内接于⊙O,
∴∠AOB=360°6=60°,
∵OA=OB=3,
∴△AOB是等边三角形,
∴AB=OA=OB=3,
故答案为:3.
15.【解析】连接OE,
∵多边形ABCDEF是正多边形,
∴∠DOE=360°6=60°,
∴∠DAE=12∠DOE=12×60°=30°,∠AED=90°,
∵⊙O的半径为2,
∴AD=2OD=4,
∴DE=12AD=12×2=1,AE=3DE=23,
∴△ADE的周长为2+4+23=6+23,
故答案为:6+23.
16.【解析】连接OC,
∵AB是⊙O内接正方形的一边,
∴∠AOB=360°÷4=90°,
∵BC是⊙O内接正六边形的一边,
∴∠AOC=360°÷6=60°,
∴∠BOC=∠AOB﹣∠AOC=90°﹣60°=30°,
∴n=360°÷30°=12;
故答案为:12;
17.【解析】如图,取AB的中点K,以AB为直径作⊙K,
∵AF⊥BE,
∴∠AFB=90°,
∵AK=BK,
∴KF=AK=BK,
∵正方形ABCD的外接圆的半径为2,
∴AB=BC=2?2=2,
∴KF=AK=KB=1,
∵∠CBK=90°,
∴CK=BK2+BC2=22+12=5,
∵CF≥CK﹣KF,
∴CF≥5-1,
∴CF的最小值为5-1.
故答案为5-1.
18.【解析】∵∠DAC的平分线交圆于E,
∴∠DAE=∠CAE,
∵∠CDE=∠CAE,
∴∠DAE=∠CDE,
∵∠AED=∠DEP,
∴△ADE∽△DPE,
∴PEDE=AEDE,
∴DE2=AE?EP;
∵EP=1,AP=3,
∴AE=4,
∴DE2=AE?EP=4,
∴DE=2
∵∠DAE=∠CAE,
∴弧DE=弧CE,
∴CE=DE=2,
∵圆内接正方形ABCD,
∴∠ADC=90,
∴AC是直径,
∴∠AEC=90,
∴AC=AE2+CE2=25,
∴r=5,
故答案为:5.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解答】(1)证明:∵四边形ABCD是正方形,
∴AD=BC,
∴AD=BC,
∵M为CD的中点,
∴DM=CM,
∴AD+DM=BC+CM,
∴AM=BM;
(2)解:连接OM,OA,OB,
∵正方形ABCD内接于⊙O,
∴∠AOB=90°,
∴∠AOM=∠BOM=12(360°﹣90°)=135°,
∴AM的度数时135°.
20.【解析】(1)如图,连接BD,
∵正方形ABCD内接于⊙O,P为BC上一点,
∴∠DBC=45°,
∵∠CPD=∠DBC,
∴∠CPD=45°.
故答案为:45;
(2)如图,作CH⊥DP于H,
∵CP=22,∠CPD=45°,
∴CH=PH=2,
∵DC=4,
∴DH=CD2-CH2=42-22=23,
∴DP=PH+DH=2+23.
21.【解答】(1)证明:在⊙O中,
∵∠BAC与∠CPB是BC对的圆周角,∠ABC与∠APC是AC所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
(2)过O作OD⊥BC于D,连接OB,
则∠OBD=30°,∠ODB=90°,
∵OB=2,
∴OD=1,
∴等边△ABC的边心距为1.
22.【解答】证明:(1)延长BP至E,使PE=PC,连接CE,如图1,
∵A、B、P、C四点共圆,
∴∠BAC+∠BPC=180°,
∵∠BPC+∠EPC=180°,
∴∠BAC=∠CPE=60°,
∵PE=PC,
∴△PCE是等边三角形,
∴CE=PC,∠E=60°;
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
∴∠BCE=∠ACP,
∵△ABC、△ECP为等边三角形,
∴CE=PC,AC=BC,
在△BEC和△APC中,
CE=PC∠BCE=∠ACPBC=AC,
∴△BEC≌△APC(SAS),
∴PA=BE=PB+PC;
(2)过点B作BE⊥PB交PA于E,连接OA,OB.如图2,
∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
∵∠APB=12∠AOB=45°,
∴BP=BE,
∴PE=2PB,
在△ABE和△CBP中,
BE=BP∠1=∠3AB=BC,
∴△ABE≌△CBP(SAS),
∴PC=AE,
∴PA=AE+PE=PC+2PB;
23.【解析】(1)如图1中,连接OA、OD.
∵四边形ABCD是正方形,
∴∠AOD=90°,
∴∠AED=12∠AOD=45°.
(2)如图2中,连接CF,CE,CA,BD,作DH⊥AE于H.
∵BF∥DE,AB∥CD,
∴∠BDE=∠DBF,∠BDC=∠ABD,
∴∠ABF=∠CDE,
∵∠CFA=∠AEC=90°,
∴∠DEC=∠AFB=135°,
∵CD=AB,
∴△CDE≌△ABF,
∴AF=CE=1,
∴AC=AE2+CE2=17,
∴AD=22AC=342,
∵∠DHE=90°,
∴∠HDE=∠HED=45°,
∴DH=HE,设DH=EH=x,
在Rt△ADH中,∵AD2=AH2+DH2,
∴344=(4﹣x)2+x2,
解得x=32或52(舍弃),
∴DE=2DH=322
24.【解析】(1)∠AOQ=60°.
在△ABP和△BCQ中,AB=BC∠ABC=∠CPB=CQ.
∴△ABP≌△BCQ(SAS).
∴∠BAP=∠CBQ.
∴∠AOQ=∠ABO+∠BAP=∠ABO+∠CBQ=∠ABC=60°;
(2)理由同(1):正方形∠AOQ=90°,正五边形∠AOQ=108°,
(3)正n边形∠AOQ=180°(n-2)n.
故答案为:90°,108°.
