3.9 弧长及扇形的面积同步练习(含解析)
文档属性
| 名称 | 3.9 弧长及扇形的面积同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 10:26:48 | ||
图片预览



文档简介
3.10弧长及扇形的面积
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,其中选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2019秋?莫旗期末)已知一个扇形的弧长为3π,所含的圆心角为120°,则半径为( )
A.9 B.3 C.92 D.322
2.(2019秋?鹿城区月考)已知扇形的弧长为8π,圆心角为120°,则扇形的半径是( )
A.6 B.8 C.12 D.24
3.(2019春?建湖县期中)如图,点A、B、C在半径为9的⊙O上,OA∥BC,∠OAB=70°,则劣弧AC的长为( )
A.6π B.7π C.72π D.632π
4.(2020春?东台市期中)如图,一块六边形绿化园地,六角都做有半径为1m的圆形喷水池,则这六个喷水池占去的绿化园地的面积(结果保留π)为( )
A.πm2 B.2πm2 C.4πm2 D.nπm2
5.(2019秋?邳州市期中)如图,在Rt△ABC中,∠ABC=90°,AB=4cm,BC=3cm,分别以A,C为圆心,以AC2的长为半径作圆.将Rt△ABC截去两个扇形,则剩余(阴影)部分的面积为( )cm2
A.6-254π B.6-2516π C.2516π D.6-52π
6.(2020?毕节市)如图,已知点C,D是以AB为直径的半圆的三等分点,弧CD的长为13π,则图中阴影部分的面积为( )
A.16π B.316π C.124π D.112π+34
7.(2019秋?玉田县期末)某盏路灯照射的空间可以看成如图所示的圆锥,它的高AO=8米,底面半径OB=6米,则圆锥的侧面积是多少平方米(结果保留π).( )
A.60π B.50π C.47.5π D.45.5π
8.(2020?新泰市二模)如图,从一块直径为4的圆形铁皮上剪出一个圆心角为90°的扇形CAB,且点C,A,B都在⊙O上,将此扇形围成一个圆锥,则该圆锥底面圆的半径是( )
A.12 B.2 C.22 D.24
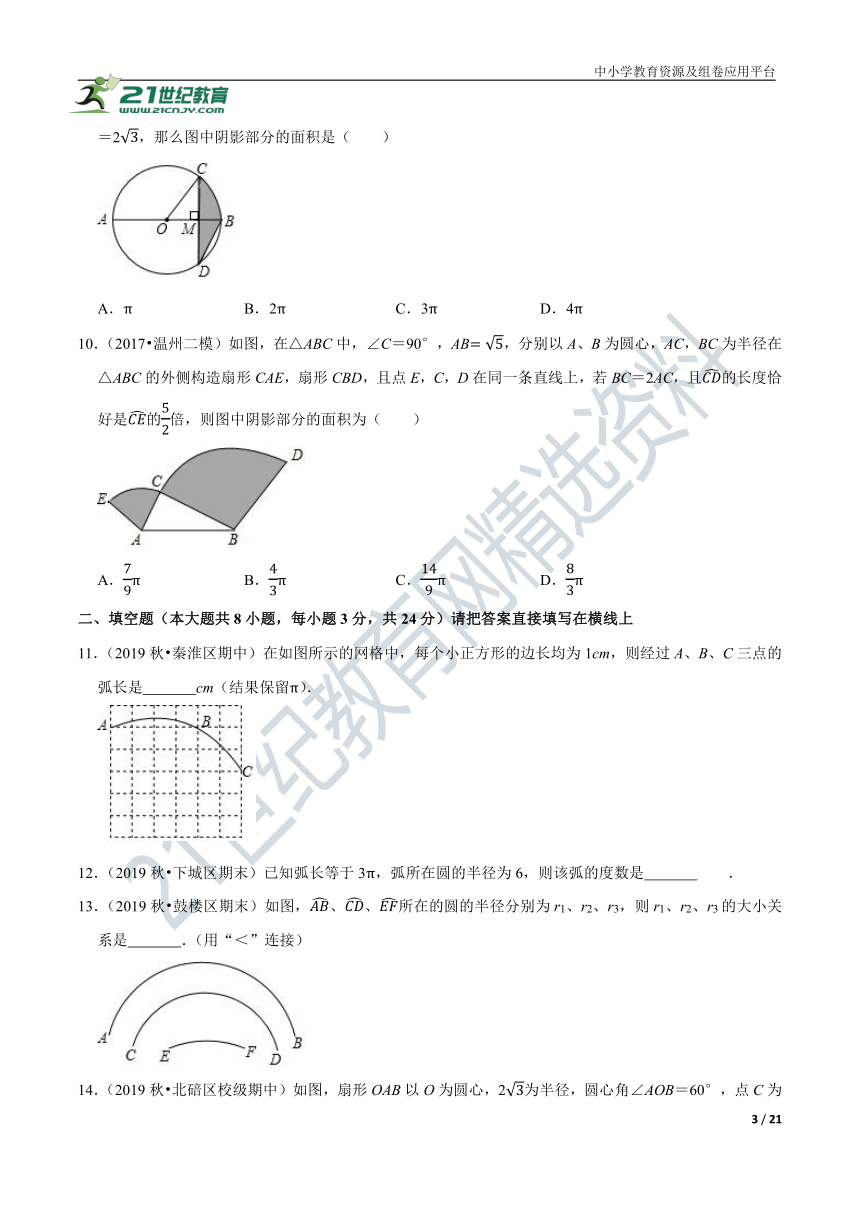
9.(2020?聊城)如图,AB是⊙O的直径,弦CD⊥AB,垂足为点M,连接OC,DB.如果OC∥DB,OC=23,那么图中阴影部分的面积是( )
A.π B.2π C.3π D.4π
10.(2017?温州二模)如图,在△ABC中,∠C=90°,AB=5,分别以A、B为圆心,AC,BC为半径在△ABC的外侧构造扇形CAE,扇形CBD,且点E,C,D在同一条直线上,若BC=2AC,且CD的长度恰好是CE的52倍,则图中阴影部分的面积为( )
A.79π B.43π C.149π D.83π
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2019秋?秦淮区期中)在如图所示的网格中,每个小正方形的边长均为1cm,则经过A、B、C三点的弧长是 cm(结果保留π).
12.(2019秋?下城区期末)已知弧长等于3π,弧所在圆的半径为6,则该弧的度数是 .
13.(2019秋?鼓楼区期末)如图,AB、CD、EF所在的圆的半径分别为r1、r2、r3,则r1、r2、r3的大小关系是 .(用“<”连接)
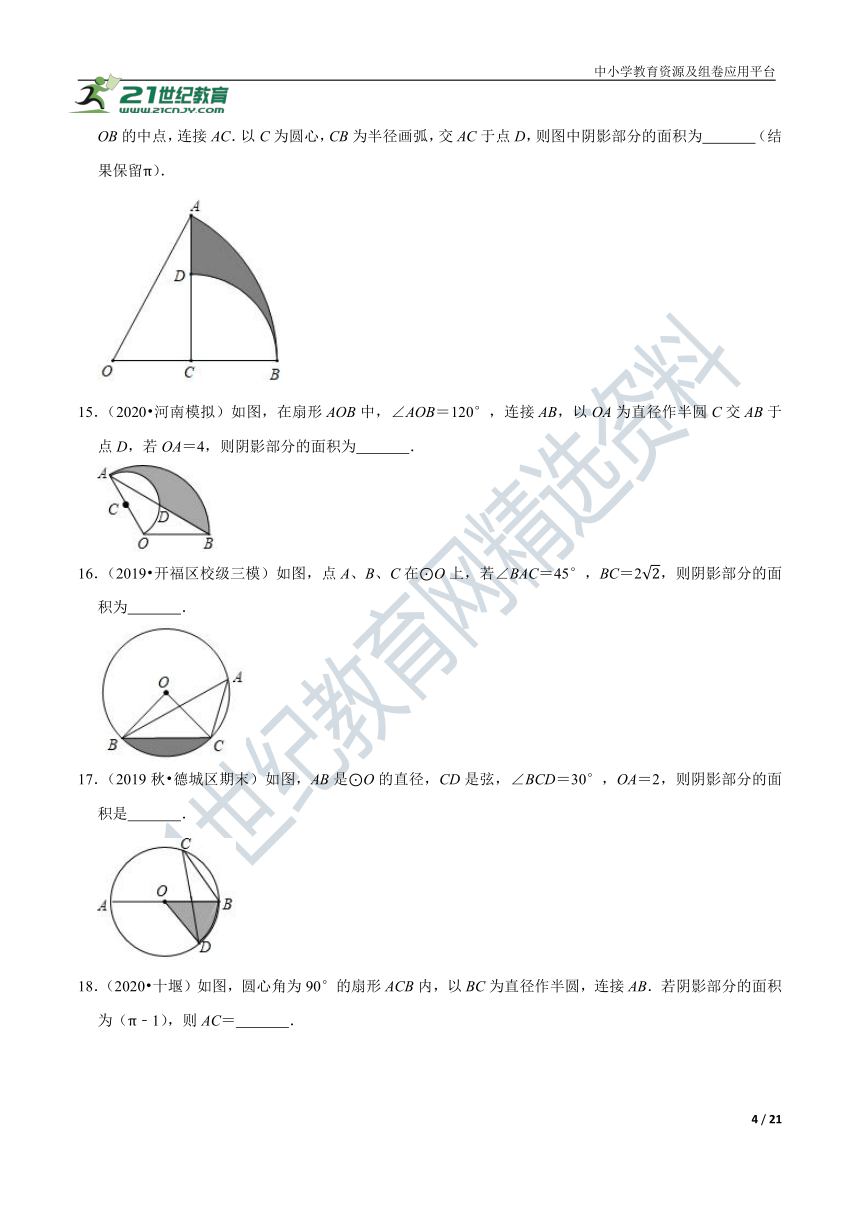
14.(2019秋?北碚区校级期中)如图,扇形OAB以O为圆心,23为半径,圆心角∠AOB=60°,点C为OB的中点,连接AC.以C为圆心,CB为半径画弧,交AC于点D,则图中阴影部分的面积为 (结果保留π).
15.(2020?河南模拟)如图,在扇形AOB中,∠AOB=120°,连接AB,以OA为直径作半圆C交AB于点D,若OA=4,则阴影部分的面积为 .
16.(2019?开福区校级三模)如图,点A、B、C在⊙O上,若∠BAC=45°,BC=22,则阴影部分的面积为 .
17.(2019秋?德城区期末)如图,AB是⊙O的直径,CD是弦,∠BCD=30°,OA=2,则阴影部分的面积是 .
18.(2020?十堰)如图,圆心角为90°的扇形ACB内,以BC为直径作半圆,连接AB.若阴影部分的面积为(π﹣1),则AC= .
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.如图,A是半径为2的⊙O外一点,OA=4,AB是⊙O的切线,B为切点,弦BC∥OA,连接AC,求阴影部分的面积.
20.(2019?遵义四模)如图,在Rt△ABC中,∠ACB=90°,以直角边BC为直径的⊙O交斜边AB于点D.点E为边AC的中点,连接DE并延长交BC的延长线于点F.
(1)求证:直线DE是⊙O的切线;
(2)若∠B=30°,AC=4,求阴影部分的面积.
21.(2018秋?黄山期末)如图,AB是⊙O的直径,弦CD⊥AB于点E,连接AC,BC.
(1)求证:∠A=∠BCD;
(2)若CD=43,∠B=60°,求扇形OAC(阴影部分)的面积.
22.(2020?龙岗区二模)如图,已知AB,CD为⊙O的直径,过点A作弦AE垂直于直径CD于F,点B恰好为DE的中点,连接BC,BE.
(1)求证:AE=BC;
(2)若AE=23,求⊙O的半径;
(3)在(2)的条件下,求阴影部分的面积.
23.(2020春?朝阳区校级月考)如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,AB=AE,BE分别交AD、AC于点F、G.
(1)证明:FA=FB;
(2)若BD=DO=2,求EC的长度.
24.(2019秋?吴兴区期末)如图,已知在矩形ABCD中,AB=2,BC=23.点P,Q分别是BC,AD边上的一个动点,连结BQ,以P为圆心,PB长为半径的⊙P交线段BQ于点E,连结PD.
(1)若DQ=3且四边形BPDQ是平行四边形时,求出⊙P的弦BE的长;
(2)在点P,Q运动的过程中,当四边形BPDQ是菱形时,求出⊙P的弦BE的长,并计算此时菱形与园重叠部分的面积.
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解析】设半径为r,∵扇形的弧长为3π,所含的圆心角为120°,
∴120?π×r180=3π,
∴r=92,
故选:C.
2.【解析】根据弧长的公式l=nπr180,
得到:8π=120πr180,
解得r=12,
故选:C.
3.【解析】连接OB,
∵OA=OB,
∴∠OBA=∠OAB=70°,
∴∠AOB=40°,
∵OA∥BC,
∴∠OBC=∠AOB=40°,
∵OB=OC,
∴∠C=∠OBC=40°,
∴∠BOC=100°,
∴∠AOC=100°+40°=140°,
∴劣弧AC的长=140?π×9180=7π,
故选:B.
4.【解析】∵六个扇形的圆心角的和=(6﹣2)×180°=720°,
∴S阴影部分=720π×12360=2π(m2),
∴这六个喷水池占去的绿化园地的面积(结果保留π)为2πm2.
故选:B.
5.【解析】∵∠C=90°,∴∠A+∠B=90°,
设∠A=α,∠B=β,则α+β=90°,
∵∠B=90°,AB=4cm,BC=3cm,
∴AC=AB2+BC2=42+32=5cm,
∴阴影的面积为12×3×4-απ?(2.5)2360-βπ?(2.5)2360=(6-2516π)cm2.
故选:B.
6.【解析】连接CD、OC、OD.
∵C,D是以AB为直径的半圆的三等分点,
∴∠AOC=∠COD=∠DOB=60°,AC=CD,
又∵OA=OC=OD,
∴△OAC、△OCD是等边三角形,
∴∠AOC=∠OCD,
∴CD∥AB,
∴S△ACD=S△OCD,
∵弧CD的长为13π,
∴60π?r180=13π,
解得:r=1,
∴S阴影=S扇形OCD=60π?12360=π6.
故选:A.
7.【解析】∵AO=8米,OB=6米,
∴AB=10米,
∴圆锥的底面周长=2×π×6=12π米,
∴S扇形=12lr=12×12π×10=60π米2.
故选:A.
8.【解析】连接BC,如图,
∵∠BAC=90°,
∴BC为⊙O的直径,BC=4,
∴AB=AC=22,
设该圆锥底面圆的半径为r,
∴2πr=90π×22180,解得r=22,
即该圆锥底面圆的半径为22.
故选:C.
9.【解析】连接OD,BC,
∵CD⊥AB,OC=OD,
∴DM=CM,∠COB=∠BOD,
∵OC∥BD,
∴∠COB=∠OBD,
∴∠BOD=∠OBD,
∴OD=DB,
∴△BOD是等边三角形,
∴∠BOD=60°,
∴∠BOC=60°,
∵DM=CM,
∴S△OBC=S△OBD,
∵OC∥DB,
∴S△OBD=S△CBD,
∴S△OBC=S△DBC,
∴图中阴影部分的面积=60?π×(23)2360=2π,
故选:B.
10.【解析】如图,连接ED,作AM⊥EC于M,BN⊥CD于N.
∵BC=2AC,
∴设AC=x,BC=2x,
∵∠C=90°,
∴x2+(2x)2=5,
∴x=1,2x=2,
AC=1,BC=2,
∵∠AMC=∠BNC=∠ACB=90°,
∴∠ACM+∠CAM=90°,∠ACM+∠BCN=90°,
∴∠BCN=∠CAM,
∵∠CBN+∠BCN=90°,
∴∠CAM+∠CBN=90°,
∵AE=AC,AM⊥EC,BC=BD,BN⊥CD,
∴∠CAE=2∠CAM,∠CBD=2∠CBN,
∴∠CAE+∠CBD=180°,
∵CD的长度恰好是CE的52倍,设∠CBD=m,∠CAE=n,
∴mπ?2180=52×n?π?1180,
∴4m=5n,
∵m+n=180°,
∴m=100°,n=80°,
∴S阴=100?π?22360+80?π?12360=4π3,
故选:B.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解析】连接BC、AB,作BC与AB的垂直平分线交于点O,点O即为A、B、C所在圆的圆心,
则OA2=22+42=20,OA=25
可知∠AOC=90°,
∴过A、B、C三点的弧:90π×25180=5π.
故答案为5π
12.【解析】设弧的圆心角为n°.
由题意:nπ?6180=3π,
解得n=90,
∴该弧的度数是90°,
故答案为90°.
13.【解析】观察图象可知:r2<r1<r3
故答案为r2<r1<r3.
14.【解析】连接AB,
∵OA=OB,∠AOB=60°,
∴△AOB为等边三角形,
∵点C为OB的中点,
∴OC=BC=3,AC⊥OB,
由勾股定理得,AC=OA2-OC2=(23)2-(3)2=3,
∴图中阴影部分的面积=60π×(23)2360-12×3×3-90π×(3)2360=54π-332,
故答案为:54π-332.
15.【解析】连接OD、CD,
∵OA为圆C的直径,
∴OD⊥AB,
∵OA=OB,∠AOB=120°,
∴AD=DB,∠OAD=30°,
∴OD=12OA=2,
由勾股定理得,AD=OA2-OD2=23,
∴△AOB的面积=12×AB×OD=43,
∵OC=CA,BD=DA,
∴CD∥OB,CD=12OB,
∴∠ACD=∠AOB=120°,△ACD的面积=14×△AOB的面积=3,
∴阴影部分的面积=120?π×42360-△AOB的面积﹣(120?π×22360-△ACD的面积)
=163π﹣43-43π+3
=4π﹣33,
故答案为:4π﹣33.
16.【解析】∵∠BAC=45°,
∴∠BOC=90°,
∴△OBC是等腰直角三角形,
∵BC=22,
∴OB=2,
∴△OBC的BC边上的高为:22OB=2,
∴S阴影=S扇形OBC﹣S△OBC=90?π×22360-12×22×2=π﹣2,
故答案为:π﹣2.
17.【解析】∵∠BCD=30°,
∴∠BOD=2∠BCD=60°,
∴阴影部分的面积=60?π?22360=23π.
故答案为23π.
18.【解析】将原图区域划分为四部分,阴影部分分别为S1,S2;两块空白分别为S3,S4,连接DC,如下图所示:
由已知得:三角形ABC为等腰直角三角形,S1+S2=π﹣1,
∵BC为直径,
∴∠CDB=90°,即CD⊥AB,
故CD=DB=DA,
∴D点为BC中点,由对称性可知CD与弦CD围成的面积与S3相等.
设AC=BC=x,
则S扇形ACB﹣S3﹣S4=S1+S2,
其中S扇ACB=90?π?x2360=πx24,
S4=S△ACB-S△BCD-S3=12?x2-12?x?x2-S3=x24-S3,
故:πx24-S3-(x24-S3)=π-1,
所以:x1=2,x2=﹣2(舍去)
故答案:2.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解析】连接OB,OC,
∵AB是圆的切线,
∴∠ABO=90°,
在直角△ABO中,OB=2,OA=4,
∴∠OAB=30°,∠AOB=60°,
∵OA∥BC,
∴∠CBO=∠AOB=60°,且S阴影部分=S扇形△BOC,
∴△BOC是等边三角形,边长是2,
∴S阴影部分=S扇形△BOC=60π×22360=2π3,即图中阴影部分的面积是2π3.
20.【解答】(1)证明:连接OD、CD,
∵OC=OD,
∴∠OCD=∠ODC,
又∵BC是⊙O的直径,
∴∠BDC=90°,
∴△ACD是直角三角形,
又∵点E是斜边AC的中点,
∴EC=ED,
∴∠ECD=∠EDC
又∵∠ECD+∠OCD=∠ACB=90度,
∴∠EDC+∠ODC=∠ODE=90°,
∴直线DE是⊙O的切线;
(2)解:由(1)已证:∠ODF=90°,
∴∠B=30°,
∴∠DOF=60°,
∴∠F=30°,
在Rt△ABC中,AC=4,
∴BC=ACtan30°=433=43,
∴OD=23,
在Rt△ODF中,DF=ODtan30°=2333=6,
∴阴影部分的面积为:12×23×6-60360π×(23)2=63-2π.
21.【解答】(1)证明:∵AB是⊙O的直径,弦CD⊥AB,
∴BC=BD,
∴∠A=∠BCD;
(2)解:∵OC=OB,∠B=60°,
∴△BOC为等边三角形,
∴∠BOC=60°,
∴∠AOC=120°,
∵AB是⊙O的直径,弦CD⊥AB,
∴CE=12CD=23,
在Rt△COE中,OC=CEsin∠COB=4,
∴扇形OAC(阴影部分)的面积=120π×42360=163π.
22.【解答】(1)证明:连接BD,
∵AB,CD为⊙O的直径,
∴∠CBD=∠AEB=90°,
∵点B恰好为DE的中点,
∴BD=EB,
∴∠A=∠C,
∵∠ABE=90°﹣∠A,∠CDB=90°﹣∠C,
∴∠ABE=∠CDB,
∴AE=BC,
∴AE=BC;
(2)解:∵过点A作弦AE垂直于直径CD于F,
∴AC=EC,
∵AE=BC,
∴AC=BE=12AE,
∴∠A=12∠ABE,
∴∠A=30°,
在Rt△ABE中,cos∠A=AEAB,
∴AB=AEcos30°=2332=4,
∴⊙O的半径为2.
(3)连接OE,
∵∠A=30°,
∴∠EOB=60°,
∴△EOB是等边三角形,
∵OB=OE=2,
∴S△EOB=12×2×2×32=3,
∴S阴=S扇形﹣S△EOB=60π×22360-3=2π3-3.
23.【解答】(1)证明:∵BC 是⊙O 的直径,
∴∠BAC=90°,
∴∠ABE+∠AGB=90°;
∵AD⊥BC,
∴∠C+∠CAD=90°;
∵AB=AE,
∴∠C=∠ABE,
∴∠AGB=∠CAD,
∵∠C=∠BAD
∴∠BAD=∠ABE
∴FA=FB.
(2)解:如图,连接AO、EO,
,
∵BD=DO=2,AD⊥BC,
∴AB=AO,
∵AO=BO,
∴AB=AO=BO,
∴△ABO是等边三角形,
∴∠AOB=60°,
∵AB=AE,
∴∠AOE=60°,
∴∠EOC=60°,
∴EC的长度=60×π×4180=43π.
24.【解答】
解:如图:
过点P作PT⊥BQ于点T,
∵AB=2,AD=BC=23,DQ=3,
∴AQ=3,
在Rt△ABQ中,根据勾股定理可得:BQ=7.
又∵四边形BPDQ是平行四边形,
∴BP=DQ=3
∵∠AQB=∠TBP,∠A=∠BTP,
∴△AQB∽△TPB,
∴BTAQ=BPBQ,
即BT3=37,
∴BT=377,
∴BE=2BT=677.
(2)设菱形BPDQ的边长为x,
则AQ=23-x,
在Rt△ABQ中,根据勾股定理,得
AB2+AQ2=BQ2,
即4+(23-x)2=x2,
解得x=433
由(1)可知:
BTx=23-xx,
∴BT=23-x=23-433=233,
∴BE=433,
∴点E、Q重合,
∴圆P经过点B、Q、D,
∴S菱形=833.
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,其中选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2019秋?莫旗期末)已知一个扇形的弧长为3π,所含的圆心角为120°,则半径为( )
A.9 B.3 C.92 D.322
2.(2019秋?鹿城区月考)已知扇形的弧长为8π,圆心角为120°,则扇形的半径是( )
A.6 B.8 C.12 D.24
3.(2019春?建湖县期中)如图,点A、B、C在半径为9的⊙O上,OA∥BC,∠OAB=70°,则劣弧AC的长为( )
A.6π B.7π C.72π D.632π
4.(2020春?东台市期中)如图,一块六边形绿化园地,六角都做有半径为1m的圆形喷水池,则这六个喷水池占去的绿化园地的面积(结果保留π)为( )
A.πm2 B.2πm2 C.4πm2 D.nπm2
5.(2019秋?邳州市期中)如图,在Rt△ABC中,∠ABC=90°,AB=4cm,BC=3cm,分别以A,C为圆心,以AC2的长为半径作圆.将Rt△ABC截去两个扇形,则剩余(阴影)部分的面积为( )cm2
A.6-254π B.6-2516π C.2516π D.6-52π
6.(2020?毕节市)如图,已知点C,D是以AB为直径的半圆的三等分点,弧CD的长为13π,则图中阴影部分的面积为( )
A.16π B.316π C.124π D.112π+34
7.(2019秋?玉田县期末)某盏路灯照射的空间可以看成如图所示的圆锥,它的高AO=8米,底面半径OB=6米,则圆锥的侧面积是多少平方米(结果保留π).( )
A.60π B.50π C.47.5π D.45.5π
8.(2020?新泰市二模)如图,从一块直径为4的圆形铁皮上剪出一个圆心角为90°的扇形CAB,且点C,A,B都在⊙O上,将此扇形围成一个圆锥,则该圆锥底面圆的半径是( )
A.12 B.2 C.22 D.24
9.(2020?聊城)如图,AB是⊙O的直径,弦CD⊥AB,垂足为点M,连接OC,DB.如果OC∥DB,OC=23,那么图中阴影部分的面积是( )
A.π B.2π C.3π D.4π
10.(2017?温州二模)如图,在△ABC中,∠C=90°,AB=5,分别以A、B为圆心,AC,BC为半径在△ABC的外侧构造扇形CAE,扇形CBD,且点E,C,D在同一条直线上,若BC=2AC,且CD的长度恰好是CE的52倍,则图中阴影部分的面积为( )
A.79π B.43π C.149π D.83π
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2019秋?秦淮区期中)在如图所示的网格中,每个小正方形的边长均为1cm,则经过A、B、C三点的弧长是 cm(结果保留π).
12.(2019秋?下城区期末)已知弧长等于3π,弧所在圆的半径为6,则该弧的度数是 .
13.(2019秋?鼓楼区期末)如图,AB、CD、EF所在的圆的半径分别为r1、r2、r3,则r1、r2、r3的大小关系是 .(用“<”连接)
14.(2019秋?北碚区校级期中)如图,扇形OAB以O为圆心,23为半径,圆心角∠AOB=60°,点C为OB的中点,连接AC.以C为圆心,CB为半径画弧,交AC于点D,则图中阴影部分的面积为 (结果保留π).
15.(2020?河南模拟)如图,在扇形AOB中,∠AOB=120°,连接AB,以OA为直径作半圆C交AB于点D,若OA=4,则阴影部分的面积为 .
16.(2019?开福区校级三模)如图,点A、B、C在⊙O上,若∠BAC=45°,BC=22,则阴影部分的面积为 .
17.(2019秋?德城区期末)如图,AB是⊙O的直径,CD是弦,∠BCD=30°,OA=2,则阴影部分的面积是 .
18.(2020?十堰)如图,圆心角为90°的扇形ACB内,以BC为直径作半圆,连接AB.若阴影部分的面积为(π﹣1),则AC= .
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.如图,A是半径为2的⊙O外一点,OA=4,AB是⊙O的切线,B为切点,弦BC∥OA,连接AC,求阴影部分的面积.
20.(2019?遵义四模)如图,在Rt△ABC中,∠ACB=90°,以直角边BC为直径的⊙O交斜边AB于点D.点E为边AC的中点,连接DE并延长交BC的延长线于点F.
(1)求证:直线DE是⊙O的切线;
(2)若∠B=30°,AC=4,求阴影部分的面积.
21.(2018秋?黄山期末)如图,AB是⊙O的直径,弦CD⊥AB于点E,连接AC,BC.
(1)求证:∠A=∠BCD;
(2)若CD=43,∠B=60°,求扇形OAC(阴影部分)的面积.
22.(2020?龙岗区二模)如图,已知AB,CD为⊙O的直径,过点A作弦AE垂直于直径CD于F,点B恰好为DE的中点,连接BC,BE.
(1)求证:AE=BC;
(2)若AE=23,求⊙O的半径;
(3)在(2)的条件下,求阴影部分的面积.
23.(2020春?朝阳区校级月考)如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,AB=AE,BE分别交AD、AC于点F、G.
(1)证明:FA=FB;
(2)若BD=DO=2,求EC的长度.
24.(2019秋?吴兴区期末)如图,已知在矩形ABCD中,AB=2,BC=23.点P,Q分别是BC,AD边上的一个动点,连结BQ,以P为圆心,PB长为半径的⊙P交线段BQ于点E,连结PD.
(1)若DQ=3且四边形BPDQ是平行四边形时,求出⊙P的弦BE的长;
(2)在点P,Q运动的过程中,当四边形BPDQ是菱形时,求出⊙P的弦BE的长,并计算此时菱形与园重叠部分的面积.
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解析】设半径为r,∵扇形的弧长为3π,所含的圆心角为120°,
∴120?π×r180=3π,
∴r=92,
故选:C.
2.【解析】根据弧长的公式l=nπr180,
得到:8π=120πr180,
解得r=12,
故选:C.
3.【解析】连接OB,
∵OA=OB,
∴∠OBA=∠OAB=70°,
∴∠AOB=40°,
∵OA∥BC,
∴∠OBC=∠AOB=40°,
∵OB=OC,
∴∠C=∠OBC=40°,
∴∠BOC=100°,
∴∠AOC=100°+40°=140°,
∴劣弧AC的长=140?π×9180=7π,
故选:B.
4.【解析】∵六个扇形的圆心角的和=(6﹣2)×180°=720°,
∴S阴影部分=720π×12360=2π(m2),
∴这六个喷水池占去的绿化园地的面积(结果保留π)为2πm2.
故选:B.
5.【解析】∵∠C=90°,∴∠A+∠B=90°,
设∠A=α,∠B=β,则α+β=90°,
∵∠B=90°,AB=4cm,BC=3cm,
∴AC=AB2+BC2=42+32=5cm,
∴阴影的面积为12×3×4-απ?(2.5)2360-βπ?(2.5)2360=(6-2516π)cm2.
故选:B.
6.【解析】连接CD、OC、OD.
∵C,D是以AB为直径的半圆的三等分点,
∴∠AOC=∠COD=∠DOB=60°,AC=CD,
又∵OA=OC=OD,
∴△OAC、△OCD是等边三角形,
∴∠AOC=∠OCD,
∴CD∥AB,
∴S△ACD=S△OCD,
∵弧CD的长为13π,
∴60π?r180=13π,
解得:r=1,
∴S阴影=S扇形OCD=60π?12360=π6.
故选:A.
7.【解析】∵AO=8米,OB=6米,
∴AB=10米,
∴圆锥的底面周长=2×π×6=12π米,
∴S扇形=12lr=12×12π×10=60π米2.
故选:A.
8.【解析】连接BC,如图,
∵∠BAC=90°,
∴BC为⊙O的直径,BC=4,
∴AB=AC=22,
设该圆锥底面圆的半径为r,
∴2πr=90π×22180,解得r=22,
即该圆锥底面圆的半径为22.
故选:C.
9.【解析】连接OD,BC,
∵CD⊥AB,OC=OD,
∴DM=CM,∠COB=∠BOD,
∵OC∥BD,
∴∠COB=∠OBD,
∴∠BOD=∠OBD,
∴OD=DB,
∴△BOD是等边三角形,
∴∠BOD=60°,
∴∠BOC=60°,
∵DM=CM,
∴S△OBC=S△OBD,
∵OC∥DB,
∴S△OBD=S△CBD,
∴S△OBC=S△DBC,
∴图中阴影部分的面积=60?π×(23)2360=2π,
故选:B.
10.【解析】如图,连接ED,作AM⊥EC于M,BN⊥CD于N.
∵BC=2AC,
∴设AC=x,BC=2x,
∵∠C=90°,
∴x2+(2x)2=5,
∴x=1,2x=2,
AC=1,BC=2,
∵∠AMC=∠BNC=∠ACB=90°,
∴∠ACM+∠CAM=90°,∠ACM+∠BCN=90°,
∴∠BCN=∠CAM,
∵∠CBN+∠BCN=90°,
∴∠CAM+∠CBN=90°,
∵AE=AC,AM⊥EC,BC=BD,BN⊥CD,
∴∠CAE=2∠CAM,∠CBD=2∠CBN,
∴∠CAE+∠CBD=180°,
∵CD的长度恰好是CE的52倍,设∠CBD=m,∠CAE=n,
∴mπ?2180=52×n?π?1180,
∴4m=5n,
∵m+n=180°,
∴m=100°,n=80°,
∴S阴=100?π?22360+80?π?12360=4π3,
故选:B.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解析】连接BC、AB,作BC与AB的垂直平分线交于点O,点O即为A、B、C所在圆的圆心,
则OA2=22+42=20,OA=25
可知∠AOC=90°,
∴过A、B、C三点的弧:90π×25180=5π.
故答案为5π
12.【解析】设弧的圆心角为n°.
由题意:nπ?6180=3π,
解得n=90,
∴该弧的度数是90°,
故答案为90°.
13.【解析】观察图象可知:r2<r1<r3
故答案为r2<r1<r3.
14.【解析】连接AB,
∵OA=OB,∠AOB=60°,
∴△AOB为等边三角形,
∵点C为OB的中点,
∴OC=BC=3,AC⊥OB,
由勾股定理得,AC=OA2-OC2=(23)2-(3)2=3,
∴图中阴影部分的面积=60π×(23)2360-12×3×3-90π×(3)2360=54π-332,
故答案为:54π-332.
15.【解析】连接OD、CD,
∵OA为圆C的直径,
∴OD⊥AB,
∵OA=OB,∠AOB=120°,
∴AD=DB,∠OAD=30°,
∴OD=12OA=2,
由勾股定理得,AD=OA2-OD2=23,
∴△AOB的面积=12×AB×OD=43,
∵OC=CA,BD=DA,
∴CD∥OB,CD=12OB,
∴∠ACD=∠AOB=120°,△ACD的面积=14×△AOB的面积=3,
∴阴影部分的面积=120?π×42360-△AOB的面积﹣(120?π×22360-△ACD的面积)
=163π﹣43-43π+3
=4π﹣33,
故答案为:4π﹣33.
16.【解析】∵∠BAC=45°,
∴∠BOC=90°,
∴△OBC是等腰直角三角形,
∵BC=22,
∴OB=2,
∴△OBC的BC边上的高为:22OB=2,
∴S阴影=S扇形OBC﹣S△OBC=90?π×22360-12×22×2=π﹣2,
故答案为:π﹣2.
17.【解析】∵∠BCD=30°,
∴∠BOD=2∠BCD=60°,
∴阴影部分的面积=60?π?22360=23π.
故答案为23π.
18.【解析】将原图区域划分为四部分,阴影部分分别为S1,S2;两块空白分别为S3,S4,连接DC,如下图所示:
由已知得:三角形ABC为等腰直角三角形,S1+S2=π﹣1,
∵BC为直径,
∴∠CDB=90°,即CD⊥AB,
故CD=DB=DA,
∴D点为BC中点,由对称性可知CD与弦CD围成的面积与S3相等.
设AC=BC=x,
则S扇形ACB﹣S3﹣S4=S1+S2,
其中S扇ACB=90?π?x2360=πx24,
S4=S△ACB-S△BCD-S3=12?x2-12?x?x2-S3=x24-S3,
故:πx24-S3-(x24-S3)=π-1,
所以:x1=2,x2=﹣2(舍去)
故答案:2.
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解析】连接OB,OC,
∵AB是圆的切线,
∴∠ABO=90°,
在直角△ABO中,OB=2,OA=4,
∴∠OAB=30°,∠AOB=60°,
∵OA∥BC,
∴∠CBO=∠AOB=60°,且S阴影部分=S扇形△BOC,
∴△BOC是等边三角形,边长是2,
∴S阴影部分=S扇形△BOC=60π×22360=2π3,即图中阴影部分的面积是2π3.
20.【解答】(1)证明:连接OD、CD,
∵OC=OD,
∴∠OCD=∠ODC,
又∵BC是⊙O的直径,
∴∠BDC=90°,
∴△ACD是直角三角形,
又∵点E是斜边AC的中点,
∴EC=ED,
∴∠ECD=∠EDC
又∵∠ECD+∠OCD=∠ACB=90度,
∴∠EDC+∠ODC=∠ODE=90°,
∴直线DE是⊙O的切线;
(2)解:由(1)已证:∠ODF=90°,
∴∠B=30°,
∴∠DOF=60°,
∴∠F=30°,
在Rt△ABC中,AC=4,
∴BC=ACtan30°=433=43,
∴OD=23,
在Rt△ODF中,DF=ODtan30°=2333=6,
∴阴影部分的面积为:12×23×6-60360π×(23)2=63-2π.
21.【解答】(1)证明:∵AB是⊙O的直径,弦CD⊥AB,
∴BC=BD,
∴∠A=∠BCD;
(2)解:∵OC=OB,∠B=60°,
∴△BOC为等边三角形,
∴∠BOC=60°,
∴∠AOC=120°,
∵AB是⊙O的直径,弦CD⊥AB,
∴CE=12CD=23,
在Rt△COE中,OC=CEsin∠COB=4,
∴扇形OAC(阴影部分)的面积=120π×42360=163π.
22.【解答】(1)证明:连接BD,
∵AB,CD为⊙O的直径,
∴∠CBD=∠AEB=90°,
∵点B恰好为DE的中点,
∴BD=EB,
∴∠A=∠C,
∵∠ABE=90°﹣∠A,∠CDB=90°﹣∠C,
∴∠ABE=∠CDB,
∴AE=BC,
∴AE=BC;
(2)解:∵过点A作弦AE垂直于直径CD于F,
∴AC=EC,
∵AE=BC,
∴AC=BE=12AE,
∴∠A=12∠ABE,
∴∠A=30°,
在Rt△ABE中,cos∠A=AEAB,
∴AB=AEcos30°=2332=4,
∴⊙O的半径为2.
(3)连接OE,
∵∠A=30°,
∴∠EOB=60°,
∴△EOB是等边三角形,
∵OB=OE=2,
∴S△EOB=12×2×2×32=3,
∴S阴=S扇形﹣S△EOB=60π×22360-3=2π3-3.
23.【解答】(1)证明:∵BC 是⊙O 的直径,
∴∠BAC=90°,
∴∠ABE+∠AGB=90°;
∵AD⊥BC,
∴∠C+∠CAD=90°;
∵AB=AE,
∴∠C=∠ABE,
∴∠AGB=∠CAD,
∵∠C=∠BAD
∴∠BAD=∠ABE
∴FA=FB.
(2)解:如图,连接AO、EO,
,
∵BD=DO=2,AD⊥BC,
∴AB=AO,
∵AO=BO,
∴AB=AO=BO,
∴△ABO是等边三角形,
∴∠AOB=60°,
∵AB=AE,
∴∠AOE=60°,
∴∠EOC=60°,
∴EC的长度=60×π×4180=43π.
24.【解答】
解:如图:
过点P作PT⊥BQ于点T,
∵AB=2,AD=BC=23,DQ=3,
∴AQ=3,
在Rt△ABQ中,根据勾股定理可得:BQ=7.
又∵四边形BPDQ是平行四边形,
∴BP=DQ=3
∵∠AQB=∠TBP,∠A=∠BTP,
∴△AQB∽△TPB,
∴BTAQ=BPBQ,
即BT3=37,
∴BT=377,
∴BE=2BT=677.
(2)设菱形BPDQ的边长为x,
则AQ=23-x,
在Rt△ABQ中,根据勾股定理,得
AB2+AQ2=BQ2,
即4+(23-x)2=x2,
解得x=433
由(1)可知:
BTx=23-xx,
∴BT=23-x=23-433=233,
∴BE=433,
∴点E、Q重合,
∴圆P经过点B、Q、D,
∴S菱形=833.
