湖北省第五届高考测评活动2020-2021学年高一上学期元月期末联考数学试题(B) Word版含答案
文档属性
| 名称 | 湖北省第五届高考测评活动2020-2021学年高一上学期元月期末联考数学试题(B) Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 624.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 09:25:12 | ||
图片预览




文档简介
2020年湖北省第五届高考测评活动高一元月期末联考
数学试卷(B卷)
本试卷共4页,22题.全卷满分150分.考试用时120分钟.
★祝考试顺利★
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.写在试卷、草稿纸和答题卡上的非答题区域均无效.
3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿纸和答题卡上的非答题区域均无效.
4.选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑.答案写在答题卡上对应的答题区域内,写在试卷、草稿纸和答题卡上的非答题区域均无效.
5.考试结束后,请将本试卷和答题卡一并上交.
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,,则( )
A. B.
C. D.
2. 下列函数与是同一个函数的是( )
A. B.
C. D.
3. 下列不等式中
①若 则; ②若, 则;
③若 则;④若 则;
其中成立有( )
A. ①②③④ B. ②④ C. ①③④ D. ②③④
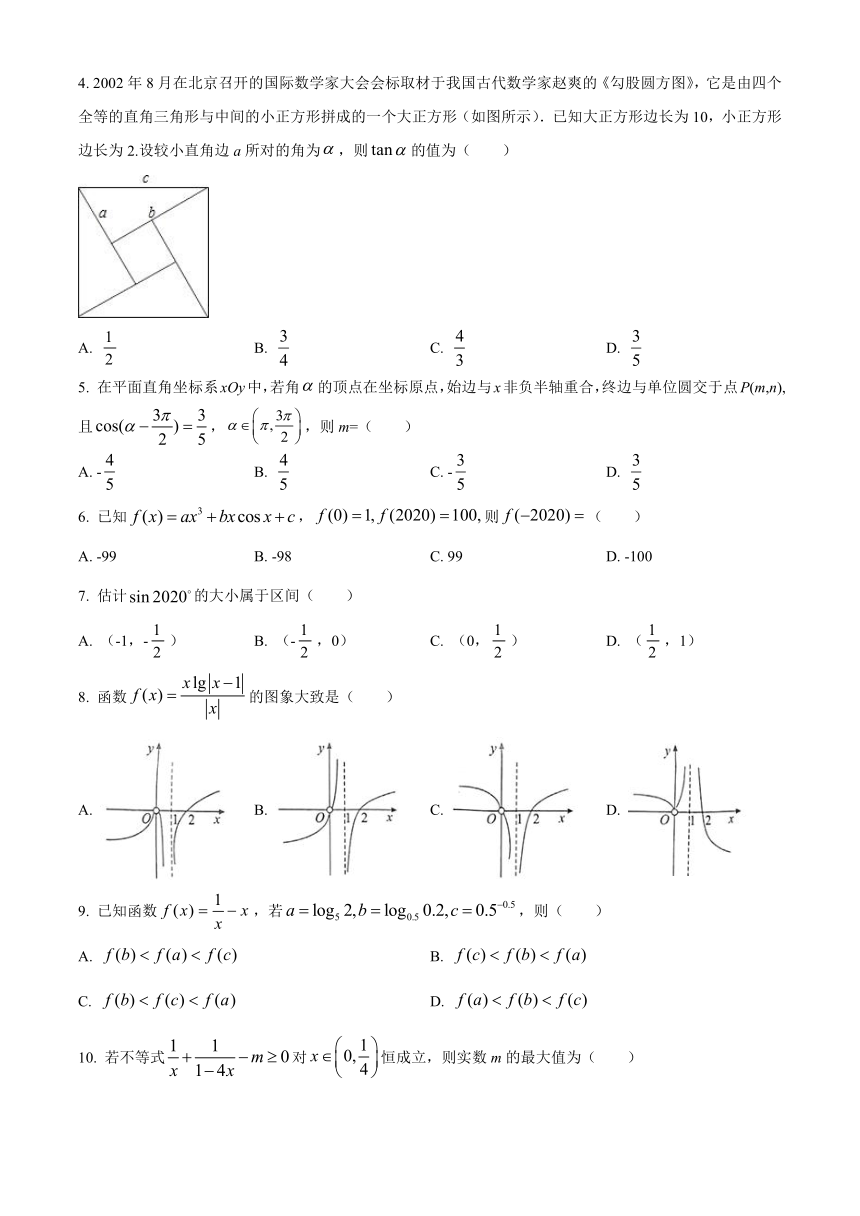
4. 2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示).已知大正方形边长为10,小正方形边长为2.设较小直角边a所对的角为,则的值为( )
A. B. C. D.
5. 在平面直角坐标系xOy中,若角的顶点在坐标原点,始边与x非负半轴重合,终边与单位圆交于点P(m,n),且,,则m=( )
A. - B. C. - D.
6. 已知,则( )
A. -99 B. -98 C. 99 D. -100
7. 估计的大小属于区间( )
A. (-1,-) B. (-,0) C. (0,) D. (,1)
8. 函数的图象大致是( )
A. B. C. D.
9. 已知函数,若,则( )
A. B.
C. D.
10. 若不等式对恒成立,则实数m的最大值为( )
A. 7 B. 8 C. 9 D. 10
11. 已知函数,若方程的解为,则( )
A. B. C. D.
12. 若定义在R上函数图象关于其图象上一点对称,对任意的实数x都有,且,则函数在区间上的零点个数最少有( )
A. 1010个 B. 1514个 C. 1515个 D. 2020个
二、填空题:本题共4小题,每小题5分,共20分.
13. 已知集合,若,则实数m取值范围为_______.
14. 已知R+,且则的最大值为_______.
15. 对下列命题:
①直线与函数图象相交,则相邻两交点的距离为;
②点 是函数的图象的一个对称中心;
③函数在上单调递减,则的取值范围为;
④函数若对R恒成立,则.
其中所有正确命题的序号为____
16. 已知函数,则f(6)=________;若方程在区间有三个不等实根,实数a的取值范围为________.
三、解答题:本大题共6小题,满分70分.解答应写出文字说明,证明过程或演算步骤.
17. (1)求值++;
(2)设求的值.
18. (1)已知关于x的不等式的解集为,求不等式的解集;
(2),a+b=2,求证.
19. 已知
(1)化简;
(2)若=2,求的值.
20. 已知函数的部分图象如图所示. .
(1)求f(x)解析式;
(2)将y=f(x)的图象先向右平移个单位,再将图象上的所有点横坐标变为原来的倍(纵坐标不变),所得到的图象对应的函数为y=g(x),求y=g(x)在上的最大值与最小值.
21. 打赢扶贫攻坚战,到2020年全面建成小康社会,是中国共产党向全世界和全国人民的承诺.一贫困户在政府扶持下结合地方特色联合当地几户贫困户创办一家农产品公司.为了振兴乡村,打好扶贫攻坚战,某市党政府开展了地标特产展销会.该公司拟定在2020年元旦展销期间举行产品促销活动,经测算该产品的年销量t万件(生产量与销量相等)与促销费用x万元满足已知2020年生产该产品还需投入成本4+t万元(不含促销费),促销费x满足当产品销量价格定为5元/件,当产品销量价格定为元/件(其中a为正常数).
(1)试将2020年该产品的利润y万元表示为促销费费x万元的函数;
(2)2020年该公司促销费投入多少万元时,公司利润最大?
22. 已知定义在R上偶函数f(x)和奇函数g(x)满足.
(1)求函数f(x)和g(x)的表达式;
(2)当时,不等式恒成立,求实数a的取值范围;
(3)若方程在上恰有一个实根,求实数m的取值范围.
2020年湖北省第五届高考测评活动高一元月期末联考
数学试卷(B卷) 答案
本试卷共4页,22题.全卷满分150分.考试用时120分钟.
★祝考试顺利★
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.写在试卷、草稿纸和答题卡上的非答题区域均无效.
3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿纸和答题卡上的非答题区域均无效.
4.选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑.答案写在答题卡上对应的答题区域内,写在试卷、草稿纸和答题卡上的非答题区域均无效.
5.考试结束后,请将本试卷和答题卡一并上交.
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,,则( )
A. B.
C. D.
【答案】B
2. 下列函数与是同一个函数的是( )
A. B.
C. D.
【答案】D
3. 下列不等式中
①若 则; ②若, 则;
③若 则;④若 则;
其中成立有( )
A. ①②③④ B. ②④ C. ①③④ D. ②③④
【答案】D
4. 2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示).已知大正方形边长为10,小正方形边长为2.设较小直角边a所对的角为,则的值为( )
A. B. C. D.
【答案】B
5. 在平面直角坐标系xOy中,若角的顶点在坐标原点,始边与x非负半轴重合,终边与单位圆交于点P(m,n),且,,则m=( )
A. - B. C. - D.
【答案】A
6. 已知,则( )
A. -99 B. -98 C. 99 D. -100
【答案】B
7. 估计的大小属于区间( )
A. (-1,-) B. (-,0) C. (0,) D. (,1)
【答案】A
8. 函数的图象大致是( )
A. B. C. D.
【答案】A
9. 已知函数,若,则( )
A. B.
C. D.
【答案】C
10. 若不等式对恒成立,则实数m的最大值为( )
A. 7 B. 8 C. 9 D. 10
【答案】C
11. 已知函数,若方程的解为,则( )
A. B. C. D.
【答案】A
12. 若定义在R上函数图象关于其图象上一点对称,对任意的实数x都有,且,则函数在区间上的零点个数最少有( )
A. 1010个 B. 1514个 C. 1515个 D. 2020个
【答案】C
二、填空题:本题共4小题,每小题5分,共20分.
13. 已知集合,若,则实数m取值范围为_______.
【答案】
14. 已知R+,且则的最大值为_______.
【答案】9
15. 对下列命题:
①直线与函数图象相交,则相邻两交点的距离为;
②点 是函数的图象的一个对称中心;
③函数在上单调递减,则的取值范围为;
④函数若对R恒成立,则.
其中所有正确命题的序号为____
【答案】①②③
16. 已知函数,则f(6)=________;若方程在区间有三个不等实根,实数a的取值范围为________.
【答案】 (1). 8 (2).
三、解答题:本大题共6小题,满分70分.解答应写出文字说明,证明过程或演算步骤.
17. (1)求值++;
(2)设求的值.
【答案】(1)123(2)1
18. (1)已知关于x的不等式的解集为,求不等式的解集;
(2),a+b=2,求证.
【答案】(1)(2)见证明
19. 已知
(1)化简;
(2)若=2,求的值.
【答案】(1)=(2)2
20. 已知函数的部分图象如图所示. .
(1)求f(x)解析式;
(2)将y=f(x)的图象先向右平移个单位,再将图象上的所有点横坐标变为原来的倍(纵坐标不变),所得到的图象对应的函数为y=g(x),求y=g(x)在上的最大值与最小值.
【答案】(1)(2)最小值与最大值分别为
21. 打赢扶贫攻坚战,到2020年全面建成小康社会,是中国共产党向全世界和全国人民的承诺.一贫困户在政府扶持下结合地方特色联合当地几户贫困户创办一家农产品公司.为了振兴乡村,打好扶贫攻坚战,某市党政府开展了地标特产展销会.该公司拟定在2020年元旦展销期间举行产品促销活动,经测算该产品的年销量t万件(生产量与销量相等)与促销费用x万元满足已知2020年生产该产品还需投入成本4+t万元(不含促销费),促销费x满足当产品销量价格定为5元/件,当产品销量价格定为元/件(其中a为正常数).
(1)试将2020年该产品的利润y万元表示为促销费费x万元的函数;
(2)2020年该公司促销费投入多少万元时,公司利润最大?
【答案】(1)(2)2万元
22. 已知定义在R上偶函数f(x)和奇函数g(x)满足.
(1)求函数f(x)和g(x)的表达式;
(2)当时,不等式恒成立,求实数a的取值范围;
(3)若方程在上恰有一个实根,求实数m的取值范围.
【答案】(1)(2)(3)
数学试卷(B卷)
本试卷共4页,22题.全卷满分150分.考试用时120分钟.
★祝考试顺利★
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.写在试卷、草稿纸和答题卡上的非答题区域均无效.
3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿纸和答题卡上的非答题区域均无效.
4.选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑.答案写在答题卡上对应的答题区域内,写在试卷、草稿纸和答题卡上的非答题区域均无效.
5.考试结束后,请将本试卷和答题卡一并上交.
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,,则( )
A. B.
C. D.
2. 下列函数与是同一个函数的是( )
A. B.
C. D.
3. 下列不等式中
①若 则; ②若, 则;
③若 则;④若 则;
其中成立有( )
A. ①②③④ B. ②④ C. ①③④ D. ②③④
4. 2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示).已知大正方形边长为10,小正方形边长为2.设较小直角边a所对的角为,则的值为( )
A. B. C. D.
5. 在平面直角坐标系xOy中,若角的顶点在坐标原点,始边与x非负半轴重合,终边与单位圆交于点P(m,n),且,,则m=( )
A. - B. C. - D.
6. 已知,则( )
A. -99 B. -98 C. 99 D. -100
7. 估计的大小属于区间( )
A. (-1,-) B. (-,0) C. (0,) D. (,1)
8. 函数的图象大致是( )
A. B. C. D.
9. 已知函数,若,则( )
A. B.
C. D.
10. 若不等式对恒成立,则实数m的最大值为( )
A. 7 B. 8 C. 9 D. 10
11. 已知函数,若方程的解为,则( )
A. B. C. D.
12. 若定义在R上函数图象关于其图象上一点对称,对任意的实数x都有,且,则函数在区间上的零点个数最少有( )
A. 1010个 B. 1514个 C. 1515个 D. 2020个
二、填空题:本题共4小题,每小题5分,共20分.
13. 已知集合,若,则实数m取值范围为_______.
14. 已知R+,且则的最大值为_______.
15. 对下列命题:
①直线与函数图象相交,则相邻两交点的距离为;
②点 是函数的图象的一个对称中心;
③函数在上单调递减,则的取值范围为;
④函数若对R恒成立,则.
其中所有正确命题的序号为____
16. 已知函数,则f(6)=________;若方程在区间有三个不等实根,实数a的取值范围为________.
三、解答题:本大题共6小题,满分70分.解答应写出文字说明,证明过程或演算步骤.
17. (1)求值++;
(2)设求的值.
18. (1)已知关于x的不等式的解集为,求不等式的解集;
(2),a+b=2,求证.
19. 已知
(1)化简;
(2)若=2,求的值.
20. 已知函数的部分图象如图所示. .
(1)求f(x)解析式;
(2)将y=f(x)的图象先向右平移个单位,再将图象上的所有点横坐标变为原来的倍(纵坐标不变),所得到的图象对应的函数为y=g(x),求y=g(x)在上的最大值与最小值.
21. 打赢扶贫攻坚战,到2020年全面建成小康社会,是中国共产党向全世界和全国人民的承诺.一贫困户在政府扶持下结合地方特色联合当地几户贫困户创办一家农产品公司.为了振兴乡村,打好扶贫攻坚战,某市党政府开展了地标特产展销会.该公司拟定在2020年元旦展销期间举行产品促销活动,经测算该产品的年销量t万件(生产量与销量相等)与促销费用x万元满足已知2020年生产该产品还需投入成本4+t万元(不含促销费),促销费x满足当产品销量价格定为5元/件,当产品销量价格定为元/件(其中a为正常数).
(1)试将2020年该产品的利润y万元表示为促销费费x万元的函数;
(2)2020年该公司促销费投入多少万元时,公司利润最大?
22. 已知定义在R上偶函数f(x)和奇函数g(x)满足.
(1)求函数f(x)和g(x)的表达式;
(2)当时,不等式恒成立,求实数a的取值范围;
(3)若方程在上恰有一个实根,求实数m的取值范围.
2020年湖北省第五届高考测评活动高一元月期末联考
数学试卷(B卷) 答案
本试卷共4页,22题.全卷满分150分.考试用时120分钟.
★祝考试顺利★
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.写在试卷、草稿纸和答题卡上的非答题区域均无效.
3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿纸和答题卡上的非答题区域均无效.
4.选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑.答案写在答题卡上对应的答题区域内,写在试卷、草稿纸和答题卡上的非答题区域均无效.
5.考试结束后,请将本试卷和答题卡一并上交.
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,,则( )
A. B.
C. D.
【答案】B
2. 下列函数与是同一个函数的是( )
A. B.
C. D.
【答案】D
3. 下列不等式中
①若 则; ②若, 则;
③若 则;④若 则;
其中成立有( )
A. ①②③④ B. ②④ C. ①③④ D. ②③④
【答案】D
4. 2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示).已知大正方形边长为10,小正方形边长为2.设较小直角边a所对的角为,则的值为( )
A. B. C. D.
【答案】B
5. 在平面直角坐标系xOy中,若角的顶点在坐标原点,始边与x非负半轴重合,终边与单位圆交于点P(m,n),且,,则m=( )
A. - B. C. - D.
【答案】A
6. 已知,则( )
A. -99 B. -98 C. 99 D. -100
【答案】B
7. 估计的大小属于区间( )
A. (-1,-) B. (-,0) C. (0,) D. (,1)
【答案】A
8. 函数的图象大致是( )
A. B. C. D.
【答案】A
9. 已知函数,若,则( )
A. B.
C. D.
【答案】C
10. 若不等式对恒成立,则实数m的最大值为( )
A. 7 B. 8 C. 9 D. 10
【答案】C
11. 已知函数,若方程的解为,则( )
A. B. C. D.
【答案】A
12. 若定义在R上函数图象关于其图象上一点对称,对任意的实数x都有,且,则函数在区间上的零点个数最少有( )
A. 1010个 B. 1514个 C. 1515个 D. 2020个
【答案】C
二、填空题:本题共4小题,每小题5分,共20分.
13. 已知集合,若,则实数m取值范围为_______.
【答案】
14. 已知R+,且则的最大值为_______.
【答案】9
15. 对下列命题:
①直线与函数图象相交,则相邻两交点的距离为;
②点 是函数的图象的一个对称中心;
③函数在上单调递减,则的取值范围为;
④函数若对R恒成立,则.
其中所有正确命题的序号为____
【答案】①②③
16. 已知函数,则f(6)=________;若方程在区间有三个不等实根,实数a的取值范围为________.
【答案】 (1). 8 (2).
三、解答题:本大题共6小题,满分70分.解答应写出文字说明,证明过程或演算步骤.
17. (1)求值++;
(2)设求的值.
【答案】(1)123(2)1
18. (1)已知关于x的不等式的解集为,求不等式的解集;
(2),a+b=2,求证.
【答案】(1)(2)见证明
19. 已知
(1)化简;
(2)若=2,求的值.
【答案】(1)=(2)2
20. 已知函数的部分图象如图所示. .
(1)求f(x)解析式;
(2)将y=f(x)的图象先向右平移个单位,再将图象上的所有点横坐标变为原来的倍(纵坐标不变),所得到的图象对应的函数为y=g(x),求y=g(x)在上的最大值与最小值.
【答案】(1)(2)最小值与最大值分别为
21. 打赢扶贫攻坚战,到2020年全面建成小康社会,是中国共产党向全世界和全国人民的承诺.一贫困户在政府扶持下结合地方特色联合当地几户贫困户创办一家农产品公司.为了振兴乡村,打好扶贫攻坚战,某市党政府开展了地标特产展销会.该公司拟定在2020年元旦展销期间举行产品促销活动,经测算该产品的年销量t万件(生产量与销量相等)与促销费用x万元满足已知2020年生产该产品还需投入成本4+t万元(不含促销费),促销费x满足当产品销量价格定为5元/件,当产品销量价格定为元/件(其中a为正常数).
(1)试将2020年该产品的利润y万元表示为促销费费x万元的函数;
(2)2020年该公司促销费投入多少万元时,公司利润最大?
【答案】(1)(2)2万元
22. 已知定义在R上偶函数f(x)和奇函数g(x)满足.
(1)求函数f(x)和g(x)的表达式;
(2)当时,不等式恒成立,求实数a的取值范围;
(3)若方程在上恰有一个实根,求实数m的取值范围.
【答案】(1)(2)(3)
同课章节目录
