江苏省常州市2020-2021学年高一上学期期末学业水平监测数学试题 Word版含答案
文档属性
| 名称 | 江苏省常州市2020-2021学年高一上学期期末学业水平监测数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 530.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 09:28:33 | ||
图片预览




文档简介
常州市教育学会期末学业水平测试
高一数学 2021 年 1月
注意事项:
1. 答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.
2. 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑. 如 需改动,用橡皮擦干净后,再选涂其他答案标号. 回答非选择题时,将答案写在答题 卡上. 写在本试卷上无效.
3. 考试结束后,将答题卡交回.
一、选择题: 本题共 8 小题,每小题 5 分,共 40 分. 在每小题给出的四个选项中,只有 一项是符合题目要求的.
1. 命题“false”的否定是
A. false B. false
C. false D. false
2. 已知集合false,false,若false,false, 则实数a的值为
A. 1 B. 2 C. 3 D.4
3. 学校操场上的铅球投郑落球区是一个半径为10米的扇形,并且沿着扇形的弧是长度
为约6米的防护栏,则扇形弧所对的圆心角的大小约为
A. false B. false C. false D. false
4. 若函数false的零点所在的区间为false,则整数a的值为
A. 0 B. 1 C. 2 D. 3
5. 函数false的图象大致为
6. 已知a,b都是正数,则“false”是“false”的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分又不必要条件
7. 17 世纪,在研究天文学的过程中,为了简化大数运算,苏格兰数学家纳皮尔发明了叉数,对数的思想方法即把乘方和乘法运算分别转化为乘法和加法,数学家拉普拉斯称赞为“对数的发明在实效上等于把天文学家的寿命延长了许多倍”. 已知false,false,设false,则N所在的区间为
A. false B. false C. false D. false
8.已知false是定义在false上的奇函数,且false,当false且false时,false.已知false,若false对false恒成立,则false的取值范围是
A. false B. false C. false D. false
二、选择题: 本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分.
9. 下列命题中,正确的有
A. 若false,则false
B. 若false,则false
C. 若false且false,则false
D. 若false且false,则false
10. 某杂志以每册2元的价格发行时,发行量为10万册.经过调查,若单册价格每提高0.2元,则发行价就减少5000册.要该杂志销售收入不少于22.4万元,每册杂志可以定价为
A. 2.5元 B. 3元 C. 3.2元 D. 3.5元
11. 对于函数false (其中false),下列结论正确的有
A. 若false恒成立,则false的最小值为2
B. 当false时,false的图象关于点false中心对称
C. 当false时,false在区间false上是单调函数
D. 当false时,false的图象可由false的图象向左平移false个单位长度得到
12. 德国著名数学家狄利克雷在数学领域成就显著, 狄利克雷函数就以其名命名,其解析
式为false关于函数false有以下四个命题,其中真命题有
A.false既不是奇函数也不是偶函数
B. false
C. false
D. false
三、填空题: 本题共 4 小题,每小题 5 分,共 20 分.
13. 若角false的终边经过点false,则false
14. 计算:false
15. 已知函数false是幂函数,且false时,false单调递减,则 false的值为
16. 已知函数false若关于x的方程false在[0,4]上有3个不相等的实数根,则实数m的取值范固是 .
四、解答题: 本大题共 6 小题,共 70 分. 请在答题卡指定区域内作答,解答时应写出必要
的文字说明,证明过程或演算步骤。
17. ( 10 分)
已知全集U=R,函数false的定义域为集合A,集合false
(1) 若false,求false;
(2) 设false.若p是q的充分不必要条件,求实数m的取值范围.
18. (12 分)
(1) 已知false,求false的值;
(2) 已知false,且false为第四象限角,求false的值.
19.(12分)已知false是定义在R 上的奇函数,当false时,false
(1) 求false的解析式;
(2) 求不等式false的解集.
3764280464947020. (12分)
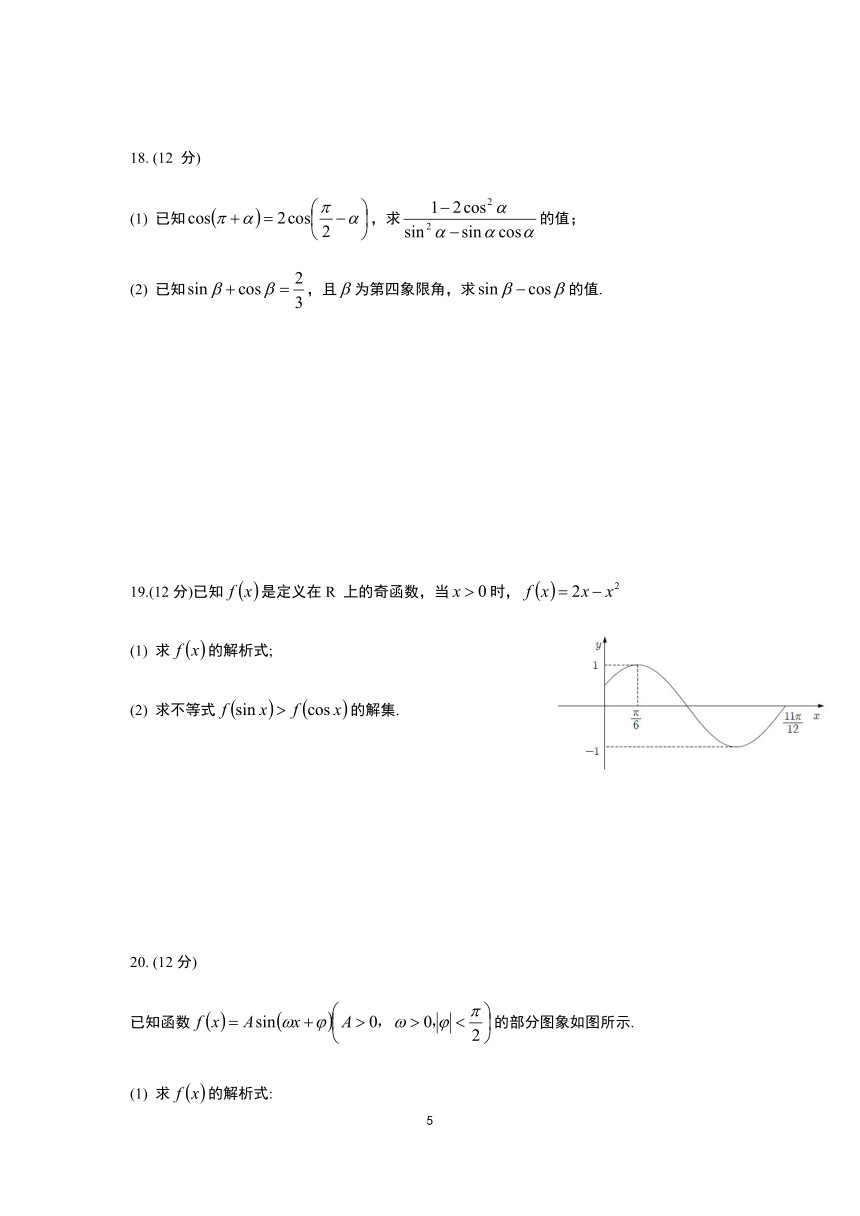
已知函数false的部分图象如图所示.
(1) 求false的解析式:
(2) 将false图象上所有点的横坐标变为原来的2倍(纵坐标不变),得到false的图
象.若false,求false的值.
21. (12分)
3426460293370设矩形ABCD的周长为20,其中false如图所示,把它沿对角线AC对折后,AB交DC 于点P.设false.
(1) 将y表示成x的函数,并求定义域:
(2) 求△ADP面积的最大值.
22. (12分)
已知函数false,函数false.
(1) 填空: 函数false的增区间为 ;
(2) 若命题“false”为真命题,求实数m的取值范围;
(3) 是否存在实数m,使函数false在[0,1]上的最大值为0?如果存如果存在,求出实数m所有的值.如果不存在,说明理由.
常州市教育学会学业水平测试
高一数学 2021 年 1月
注意事项:
1. 答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.
2. 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑. 如 需改动,用橡皮擦干净后,再选涂其他答案标号. 回答非选择题时,将答案写在答题 卡上. 写在本试卷上无效.
3. 考试结束后,将答题卡交回.
一、选择题: 本题共 8 小题,每小题 5 分,共 40 分. 在每小题给出的四个选项中,只有 一项是符合题目要求的.
1. 命题“false”的否定是
A. false B. false
C. false D. false
【答案】D
【考点】全称量词命题的否定
【解析】由题意,全称量词命题的否定需要将“false”改为“false”,结论否定即可,所以答案选D.
2. 已知集合false,false,若false,false, 则实数a的值为
A. 1 B. 2 C. 3 D.4
【答案】B
【考点】集合的运算
【解析】由题意可知当集合M为双元素集合时,false,因为false,false,false,则不符合题意,所以集合M为单元素集合,即false,故答案选B.
3. 学校操场上的铅球投郑落球区是一个半径为10米的扇形,并且沿着扇形的弧是长度
为约6米的防护栏,则扇形弧所对的圆心角的大小约为
A. false B. false C. false D. false
【答案】A
【考点】弧度制与角度制、扇形的弧长
【解析】由题意可知弧长false,且false,所以false,故答案选A.
4. 若函数false的零点所在的区间为false,则整数a的值为
A. 0 B. 1 C. 2 D. 3
【答案】C
【考点】函数的零点概念及零点存在性定理的应用
【解析】由题意可知false,false,false,所以满足false,所以零点所在的区间为false,故答案选C.
5. 函数false的图象大致为
【答案】D
【考点】函数的图象识别与判断
【解析】由题意可知该函数false,满足false,则函数为奇函数,所以选项A、C错误,可排除;因为false,false,显然false,所以排除选项B,故答案选D.
6. 已知a,b都是正数,则“false”是“false”的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分又不必要条件
【答案】B
【考点】逻辑用语中条件的判断
【解析】由题意可知当false时,可取false,显然不满足false;当false时,且false,所以false,即false,解得false,所以“false”是“false”的必要不充分条件,故答案选B.
7. 17 世纪,在研究天文学的过程中,为了简化大数运算,苏格兰数学家纳皮尔发明了叉数,对数的思想方法即把乘方和乘法运算分别转化为乘法和加法,数学家拉普拉斯称赞为“对数的发明在实效上等于把天文学家的寿命延长了许多倍”. 已知false,false,设false,则N所在的区间为
A. false B. false C. false D. false
【答案】C
【考点】指对数的运算
【解析】由题意对N取常用对数,得false=
false,则false,故答案选C.
8.已知false是定义在false上的奇函数,且false,当false且false时,false.已知false,若false对false恒成立,则false的取值范围是
A. false B. false C. false D. false
【答案】A
【考点】函数的性质综合
【解析】由题意false是在false上的奇函数,且当false且false时,即false,false可化为false,则false在false上单调递增,又false,所以false,所以false,则false时,false对false恒成立,即false对false恒成立,此时false,则化简为false对false恒成立,即false,因为false,所以false
解得false,故答案选A.
二、选择题: 本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分.
9. 下列命题中,正确的有
A. 若false,则false
B. 若false,则false
C. 若false且false,则false
D. 若false且false,则false
【答案】BC
【考点】不等式的基本性质
【解析】
法一:由题意可取特殊值验证,对于A选项,取false,当false时,不能推出false,故选项A错误;对于选项B,取false,则false,故选项B正确;对于选项C,取false,可得false,故选项C正确;对于选项D,取false,可得false,故选项D正确;所以答案选BC.
法二:由题意,对于A选项,由不等式的基本性质可得,当false时,不false能推出,故选项A错误;对于选项B,因为false,所以false且false,则false,故选项B正确;对于选项C,因为false且false,所以false,所以false,故选项C正确;对于选项D,因为false且false,所以false,所以false,所以false,故选项D正确;所以答案选BC.
10. 某杂志以每册2元的价格发行时,发行量为10万册.经过调查,若单册价格每提高0.2元,则发行价就减少5000册.要该杂志销售收入不少于22.4万元,每册杂志可以定价为
A. 2.5元 B. 3元 C. 3.2元 D. 3.5元
【答案】BC
【考点】解决实际问题
【解析】由题意可设杂志最高定价为x元,总销售收入为y元,则false,因为销售收入不少于22.4万元时,可得到false,解得false,所以答案选BC.
11. 对于函数false (其中false),下列结论正确的有
A. 若false恒成立,则false的最小值为2
B. 当false时,false的图象关于点false中心对称
C. 当false时,false在区间false上是单调函数
D. 当false时,false的图象可由false的图象向左平移false个单位长度得到
【答案】ABD
【考点】三角函数的图象与性质及变换
【解析】由题意,对于选项A,若false恒成立,则false,则false,解得false,因为false,所以false的最小值为2,故选项A正确;对于选项B,当false时,函数解析式为false,且false,所以false的图象关于点false中心对称,故选项B正确;对于选项C,当false时,函数解析式为false,因为false,所以false,则函数false在false上单调递增,在false上单调递减,故选项C错误;对于选项D,当false时,函数解析式为false,所以false的图象可由false的图象向左平移false个单位长度得到,故选项D正确;所以答案选ABD.
12. 德国著名数学家狄利克雷在数学领域成就显著, 狄利克雷函数就以其名命名,其解析
式为false关于函数false有以下四个命题,其中真命题有
A.false既不是奇函数也不是偶函数
B. false
C. false
D. false
【答案】BCD
【考点】新定义函数的性质及应用
【解析】由题意,对于选项A,当x为有理数时,false为有理数,则false,同理当x为无理数时,false为无理数,则false,所以当false时,false,所以函数为偶函数,故选项A错误;对于选项B,当x为有理数时,false为有理数,所以false,x为无理数时,false为无理数,false,所以false,故选项B正确;对于选项C,当x为有理数时,false,当x为无理数时,false,所以false,故选项C正确;对于选项D,当x 、y均为无理数,可令false时,false为无理数,则false,false满足false,所以false,故选项D正确;所以答案选BCD.
三、填空题: 本题共 4 小题,每小题 5 分,共 20 分.
13. 若角false的终边经过点false,则false
【答案】false
【考点】三角函数的概念、诱导公式
【解析】由题意false,则false,故答案为false.
14. 计算:false
【答案】10
【考点】指对数运算
【解析】由题意,原式false,故答案为10.
15. 已知函数false是幂函数,且false时,false单调递减,则 false的值为
【答案】false
【考点】幂函数的概念及性质
【解析】由题意可得false,解得false,当false时,false在false上单调递减,满足题意,所以false;当false时,false在false上单调递增,不满足题意,故舍去,综上,false,false.
16. 已知函数false若关于x的方程false在[0,4]上有3个不相等的实数根,则实数m的取值范固是 .
【答案】false
【考点】用数形结合思想解决函数的零点问题
【解析】由题意false,则原方程可化为false在[0,4]上有3个不相等的实数根,即函数false的图象与函数false的图象在[0,4]上有三个交点,所以false,可作出函数false的图象,由图像可知在[0,4]上有三个交点,得到false.或函数false的图象可先作出函数false的图象,再向下平移false个单位长度,最后再把x轴下方的图象翻折到x轴上方得到.
四、解答题: 本大题共 6 小题,共 70 分. 请在答题卡指定区域内作答,解答时应写出必要
的文字说明,证明过程或演算步骤。
17. ( 10 分)
已知全集U=R,函数false的定义域为集合A,集合false
(1) 若false,求false;
(2) 设false.若p是q的充分不必要条件,求实数m的取值范围.
【考点】集合的运算、逻辑用语中条件的应用
【解析】
(1)由false化简得false,解得false,所以false, ………2分
当false时,false, ………………………3分
false. ………………………………5分
(2)false, ……………7分
因为p是q的充分不必要条件,所以AB, ……………………8分
所以false,解得false. ……………………10分
18. (12 分)
(1) 已知false,求false的值;
(2) 已知false,且false为第四象限角,求false的值.
【考点】三角函数:同角三角函数关系式、诱导公式综合应用
【解析】
(1)由false得false, …………………………2分
显然false,否则false矛盾,…………………3分
所以false. …………………………4分
所以false
false. ……………………………6分
(2)由false平方得false,
所以false, ………………………8分
所以false, ………………………10分
因为false为第四象限,false,
所以false. ………………………12分
19.(12分)已知false是定义在R 上的奇函数,当false时,false
(1) 求false的解析式;
(2) 求不等式false的解集.
【考点】函数的奇偶性及其应用
【解析】
(1)当false时,false,所以false
因为false是奇函数,所以false, …………………………3分
又因为false是定义在R 上的奇函数,所以false, …………………………4分
所以false. …………………………5分
(2)因为当false时,false,所以false在false上递增,
当false时,false所以false在false上递增,
所以false在false上递增, ………………………8分
因为false,所以由false可得false, …………10分
37261807322820所以不等式的解集为false. …………………12分
20. (12分)
已知函数false的部分图象如图所示.
(1) 求false的解析式:
(2) 将false图象上所有点的横坐标变为原来的2倍(纵坐标不变),得到false的图象.若false,求false的值.
【考点】三角函数的图象与性质、诱导公式、同角三角函数关系综合应用
【解析】
(1)由图可知false, …………………………1分
由false得false,所以false, …………………………3分
所以false.
因为false,所以false,即false,
因为false,所以false,所以false. ………………………5分
(1)由题意,false,由false得false, ………………7分
false
false ………………10分
false. ………………………12分
21. (12分)
3426460293370设矩形ABCD的周长为20,其中false如图所示,把它沿对角线AC对折后,AB交DC 于点P.设false.
(1) 将y表示成x的函数,并求定义域:
(2) 求△ADP面积的最大值.
【考点】运用基本不等式解决实际问题
【解析】
(1)因为矩形ABCD的周长为20,false,所以false,
由false得false. ……………………………………2分
由对称性可知,false,所以false,
因为false,所以false,
解得false,定义域为false. ……………………………………6分
(2)△ADP的面积false,false.…8分
令false,则false,false,
false,
因为false,所以false,当且仅当false时取“=”,
所以false,
所以△ADP的面积的最大值为false. ……………………………………12分
22. (12分)
已知函数false,函数false.
(1) 填空: 函数false的增区间为 ;
(2) 若命题“false”为真命题,求实数m的取值范围;
(3) 是否存在实数m,使函数false在[0,1]上的最大值为0?如果存如果存在,求出实数m所有的值.如果不存在,说明理由.
【考点】函数的单调性、存在性问题求参数的取值范围、函数最值的综合应用
【解析】
(1)false的增区间为false.(写开区间亦可) …………………………2分
(2)由题意false,
令false,当且仅当false时取“=”,
“false”为真命题可转化为“false”为真命题,………4分
因为false,当且仅当false时取“=”,
所以false,
所以false. ………………………6分
(3)由(1)可知,当false时,false,记false,
若函数false在[0,1]上的最大值为0,则
①当false即false时,false在false上的最小值为1,
因为false图象的对称轴false,所以false,
解得false,符合题意; ………………8分
②当false即false时,false在false上的最大值为1,且false恒成立,
因为false的图象是开口向上的抛物线,在false上的最大值只可能为false或false,
若false,则false,不合题意;
若false,则false,此时对称轴false,
由false,不合题意. ………………11分
综上所述,只有false符合条件. ………………………12分
注:如果先考虑false时,false恒成立,由false,可得false,可以避免讨论,同样得分.
高一数学 2021 年 1月
注意事项:
1. 答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.
2. 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑. 如 需改动,用橡皮擦干净后,再选涂其他答案标号. 回答非选择题时,将答案写在答题 卡上. 写在本试卷上无效.
3. 考试结束后,将答题卡交回.
一、选择题: 本题共 8 小题,每小题 5 分,共 40 分. 在每小题给出的四个选项中,只有 一项是符合题目要求的.
1. 命题“false”的否定是
A. false B. false
C. false D. false
2. 已知集合false,false,若false,false, 则实数a的值为
A. 1 B. 2 C. 3 D.4
3. 学校操场上的铅球投郑落球区是一个半径为10米的扇形,并且沿着扇形的弧是长度
为约6米的防护栏,则扇形弧所对的圆心角的大小约为
A. false B. false C. false D. false
4. 若函数false的零点所在的区间为false,则整数a的值为
A. 0 B. 1 C. 2 D. 3
5. 函数false的图象大致为
6. 已知a,b都是正数,则“false”是“false”的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分又不必要条件
7. 17 世纪,在研究天文学的过程中,为了简化大数运算,苏格兰数学家纳皮尔发明了叉数,对数的思想方法即把乘方和乘法运算分别转化为乘法和加法,数学家拉普拉斯称赞为“对数的发明在实效上等于把天文学家的寿命延长了许多倍”. 已知false,false,设false,则N所在的区间为
A. false B. false C. false D. false
8.已知false是定义在false上的奇函数,且false,当false且false时,false.已知false,若false对false恒成立,则false的取值范围是
A. false B. false C. false D. false
二、选择题: 本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分.
9. 下列命题中,正确的有
A. 若false,则false
B. 若false,则false
C. 若false且false,则false
D. 若false且false,则false
10. 某杂志以每册2元的价格发行时,发行量为10万册.经过调查,若单册价格每提高0.2元,则发行价就减少5000册.要该杂志销售收入不少于22.4万元,每册杂志可以定价为
A. 2.5元 B. 3元 C. 3.2元 D. 3.5元
11. 对于函数false (其中false),下列结论正确的有
A. 若false恒成立,则false的最小值为2
B. 当false时,false的图象关于点false中心对称
C. 当false时,false在区间false上是单调函数
D. 当false时,false的图象可由false的图象向左平移false个单位长度得到
12. 德国著名数学家狄利克雷在数学领域成就显著, 狄利克雷函数就以其名命名,其解析
式为false关于函数false有以下四个命题,其中真命题有
A.false既不是奇函数也不是偶函数
B. false
C. false
D. false
三、填空题: 本题共 4 小题,每小题 5 分,共 20 分.
13. 若角false的终边经过点false,则false
14. 计算:false
15. 已知函数false是幂函数,且false时,false单调递减,则 false的值为
16. 已知函数false若关于x的方程false在[0,4]上有3个不相等的实数根,则实数m的取值范固是 .
四、解答题: 本大题共 6 小题,共 70 分. 请在答题卡指定区域内作答,解答时应写出必要
的文字说明,证明过程或演算步骤。
17. ( 10 分)
已知全集U=R,函数false的定义域为集合A,集合false
(1) 若false,求false;
(2) 设false.若p是q的充分不必要条件,求实数m的取值范围.
18. (12 分)
(1) 已知false,求false的值;
(2) 已知false,且false为第四象限角,求false的值.
19.(12分)已知false是定义在R 上的奇函数,当false时,false
(1) 求false的解析式;
(2) 求不等式false的解集.
3764280464947020. (12分)
已知函数false的部分图象如图所示.
(1) 求false的解析式:
(2) 将false图象上所有点的横坐标变为原来的2倍(纵坐标不变),得到false的图
象.若false,求false的值.
21. (12分)
3426460293370设矩形ABCD的周长为20,其中false如图所示,把它沿对角线AC对折后,AB交DC 于点P.设false.
(1) 将y表示成x的函数,并求定义域:
(2) 求△ADP面积的最大值.
22. (12分)
已知函数false,函数false.
(1) 填空: 函数false的增区间为 ;
(2) 若命题“false”为真命题,求实数m的取值范围;
(3) 是否存在实数m,使函数false在[0,1]上的最大值为0?如果存如果存在,求出实数m所有的值.如果不存在,说明理由.
常州市教育学会学业水平测试
高一数学 2021 年 1月
注意事项:
1. 答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.
2. 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑. 如 需改动,用橡皮擦干净后,再选涂其他答案标号. 回答非选择题时,将答案写在答题 卡上. 写在本试卷上无效.
3. 考试结束后,将答题卡交回.
一、选择题: 本题共 8 小题,每小题 5 分,共 40 分. 在每小题给出的四个选项中,只有 一项是符合题目要求的.
1. 命题“false”的否定是
A. false B. false
C. false D. false
【答案】D
【考点】全称量词命题的否定
【解析】由题意,全称量词命题的否定需要将“false”改为“false”,结论否定即可,所以答案选D.
2. 已知集合false,false,若false,false, 则实数a的值为
A. 1 B. 2 C. 3 D.4
【答案】B
【考点】集合的运算
【解析】由题意可知当集合M为双元素集合时,false,因为false,false,false,则不符合题意,所以集合M为单元素集合,即false,故答案选B.
3. 学校操场上的铅球投郑落球区是一个半径为10米的扇形,并且沿着扇形的弧是长度
为约6米的防护栏,则扇形弧所对的圆心角的大小约为
A. false B. false C. false D. false
【答案】A
【考点】弧度制与角度制、扇形的弧长
【解析】由题意可知弧长false,且false,所以false,故答案选A.
4. 若函数false的零点所在的区间为false,则整数a的值为
A. 0 B. 1 C. 2 D. 3
【答案】C
【考点】函数的零点概念及零点存在性定理的应用
【解析】由题意可知false,false,false,所以满足false,所以零点所在的区间为false,故答案选C.
5. 函数false的图象大致为
【答案】D
【考点】函数的图象识别与判断
【解析】由题意可知该函数false,满足false,则函数为奇函数,所以选项A、C错误,可排除;因为false,false,显然false,所以排除选项B,故答案选D.
6. 已知a,b都是正数,则“false”是“false”的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分又不必要条件
【答案】B
【考点】逻辑用语中条件的判断
【解析】由题意可知当false时,可取false,显然不满足false;当false时,且false,所以false,即false,解得false,所以“false”是“false”的必要不充分条件,故答案选B.
7. 17 世纪,在研究天文学的过程中,为了简化大数运算,苏格兰数学家纳皮尔发明了叉数,对数的思想方法即把乘方和乘法运算分别转化为乘法和加法,数学家拉普拉斯称赞为“对数的发明在实效上等于把天文学家的寿命延长了许多倍”. 已知false,false,设false,则N所在的区间为
A. false B. false C. false D. false
【答案】C
【考点】指对数的运算
【解析】由题意对N取常用对数,得false=
false,则false,故答案选C.
8.已知false是定义在false上的奇函数,且false,当false且false时,false.已知false,若false对false恒成立,则false的取值范围是
A. false B. false C. false D. false
【答案】A
【考点】函数的性质综合
【解析】由题意false是在false上的奇函数,且当false且false时,即false,false可化为false,则false在false上单调递增,又false,所以false,所以false,则false时,false对false恒成立,即false对false恒成立,此时false,则化简为false对false恒成立,即false,因为false,所以false
解得false,故答案选A.
二、选择题: 本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分.
9. 下列命题中,正确的有
A. 若false,则false
B. 若false,则false
C. 若false且false,则false
D. 若false且false,则false
【答案】BC
【考点】不等式的基本性质
【解析】
法一:由题意可取特殊值验证,对于A选项,取false,当false时,不能推出false,故选项A错误;对于选项B,取false,则false,故选项B正确;对于选项C,取false,可得false,故选项C正确;对于选项D,取false,可得false,故选项D正确;所以答案选BC.
法二:由题意,对于A选项,由不等式的基本性质可得,当false时,不false能推出,故选项A错误;对于选项B,因为false,所以false且false,则false,故选项B正确;对于选项C,因为false且false,所以false,所以false,故选项C正确;对于选项D,因为false且false,所以false,所以false,所以false,故选项D正确;所以答案选BC.
10. 某杂志以每册2元的价格发行时,发行量为10万册.经过调查,若单册价格每提高0.2元,则发行价就减少5000册.要该杂志销售收入不少于22.4万元,每册杂志可以定价为
A. 2.5元 B. 3元 C. 3.2元 D. 3.5元
【答案】BC
【考点】解决实际问题
【解析】由题意可设杂志最高定价为x元,总销售收入为y元,则false,因为销售收入不少于22.4万元时,可得到false,解得false,所以答案选BC.
11. 对于函数false (其中false),下列结论正确的有
A. 若false恒成立,则false的最小值为2
B. 当false时,false的图象关于点false中心对称
C. 当false时,false在区间false上是单调函数
D. 当false时,false的图象可由false的图象向左平移false个单位长度得到
【答案】ABD
【考点】三角函数的图象与性质及变换
【解析】由题意,对于选项A,若false恒成立,则false,则false,解得false,因为false,所以false的最小值为2,故选项A正确;对于选项B,当false时,函数解析式为false,且false,所以false的图象关于点false中心对称,故选项B正确;对于选项C,当false时,函数解析式为false,因为false,所以false,则函数false在false上单调递增,在false上单调递减,故选项C错误;对于选项D,当false时,函数解析式为false,所以false的图象可由false的图象向左平移false个单位长度得到,故选项D正确;所以答案选ABD.
12. 德国著名数学家狄利克雷在数学领域成就显著, 狄利克雷函数就以其名命名,其解析
式为false关于函数false有以下四个命题,其中真命题有
A.false既不是奇函数也不是偶函数
B. false
C. false
D. false
【答案】BCD
【考点】新定义函数的性质及应用
【解析】由题意,对于选项A,当x为有理数时,false为有理数,则false,同理当x为无理数时,false为无理数,则false,所以当false时,false,所以函数为偶函数,故选项A错误;对于选项B,当x为有理数时,false为有理数,所以false,x为无理数时,false为无理数,false,所以false,故选项B正确;对于选项C,当x为有理数时,false,当x为无理数时,false,所以false,故选项C正确;对于选项D,当x 、y均为无理数,可令false时,false为无理数,则false,false满足false,所以false,故选项D正确;所以答案选BCD.
三、填空题: 本题共 4 小题,每小题 5 分,共 20 分.
13. 若角false的终边经过点false,则false
【答案】false
【考点】三角函数的概念、诱导公式
【解析】由题意false,则false,故答案为false.
14. 计算:false
【答案】10
【考点】指对数运算
【解析】由题意,原式false,故答案为10.
15. 已知函数false是幂函数,且false时,false单调递减,则 false的值为
【答案】false
【考点】幂函数的概念及性质
【解析】由题意可得false,解得false,当false时,false在false上单调递减,满足题意,所以false;当false时,false在false上单调递增,不满足题意,故舍去,综上,false,false.
16. 已知函数false若关于x的方程false在[0,4]上有3个不相等的实数根,则实数m的取值范固是 .
【答案】false
【考点】用数形结合思想解决函数的零点问题
【解析】由题意false,则原方程可化为false在[0,4]上有3个不相等的实数根,即函数false的图象与函数false的图象在[0,4]上有三个交点,所以false,可作出函数false的图象,由图像可知在[0,4]上有三个交点,得到false.或函数false的图象可先作出函数false的图象,再向下平移false个单位长度,最后再把x轴下方的图象翻折到x轴上方得到.
四、解答题: 本大题共 6 小题,共 70 分. 请在答题卡指定区域内作答,解答时应写出必要
的文字说明,证明过程或演算步骤。
17. ( 10 分)
已知全集U=R,函数false的定义域为集合A,集合false
(1) 若false,求false;
(2) 设false.若p是q的充分不必要条件,求实数m的取值范围.
【考点】集合的运算、逻辑用语中条件的应用
【解析】
(1)由false化简得false,解得false,所以false, ………2分
当false时,false, ………………………3分
false. ………………………………5分
(2)false, ……………7分
因为p是q的充分不必要条件,所以AB, ……………………8分
所以false,解得false. ……………………10分
18. (12 分)
(1) 已知false,求false的值;
(2) 已知false,且false为第四象限角,求false的值.
【考点】三角函数:同角三角函数关系式、诱导公式综合应用
【解析】
(1)由false得false, …………………………2分
显然false,否则false矛盾,…………………3分
所以false. …………………………4分
所以false
false. ……………………………6分
(2)由false平方得false,
所以false, ………………………8分
所以false, ………………………10分
因为false为第四象限,false,
所以false. ………………………12分
19.(12分)已知false是定义在R 上的奇函数,当false时,false
(1) 求false的解析式;
(2) 求不等式false的解集.
【考点】函数的奇偶性及其应用
【解析】
(1)当false时,false,所以false
因为false是奇函数,所以false, …………………………3分
又因为false是定义在R 上的奇函数,所以false, …………………………4分
所以false. …………………………5分
(2)因为当false时,false,所以false在false上递增,
当false时,false所以false在false上递增,
所以false在false上递增, ………………………8分
因为false,所以由false可得false, …………10分
37261807322820所以不等式的解集为false. …………………12分
20. (12分)
已知函数false的部分图象如图所示.
(1) 求false的解析式:
(2) 将false图象上所有点的横坐标变为原来的2倍(纵坐标不变),得到false的图象.若false,求false的值.
【考点】三角函数的图象与性质、诱导公式、同角三角函数关系综合应用
【解析】
(1)由图可知false, …………………………1分
由false得false,所以false, …………………………3分
所以false.
因为false,所以false,即false,
因为false,所以false,所以false. ………………………5分
(1)由题意,false,由false得false, ………………7分
false
false ………………10分
false. ………………………12分
21. (12分)
3426460293370设矩形ABCD的周长为20,其中false如图所示,把它沿对角线AC对折后,AB交DC 于点P.设false.
(1) 将y表示成x的函数,并求定义域:
(2) 求△ADP面积的最大值.
【考点】运用基本不等式解决实际问题
【解析】
(1)因为矩形ABCD的周长为20,false,所以false,
由false得false. ……………………………………2分
由对称性可知,false,所以false,
因为false,所以false,
解得false,定义域为false. ……………………………………6分
(2)△ADP的面积false,false.…8分
令false,则false,false,
false,
因为false,所以false,当且仅当false时取“=”,
所以false,
所以△ADP的面积的最大值为false. ……………………………………12分
22. (12分)
已知函数false,函数false.
(1) 填空: 函数false的增区间为 ;
(2) 若命题“false”为真命题,求实数m的取值范围;
(3) 是否存在实数m,使函数false在[0,1]上的最大值为0?如果存如果存在,求出实数m所有的值.如果不存在,说明理由.
【考点】函数的单调性、存在性问题求参数的取值范围、函数最值的综合应用
【解析】
(1)false的增区间为false.(写开区间亦可) …………………………2分
(2)由题意false,
令false,当且仅当false时取“=”,
“false”为真命题可转化为“false”为真命题,………4分
因为false,当且仅当false时取“=”,
所以false,
所以false. ………………………6分
(3)由(1)可知,当false时,false,记false,
若函数false在[0,1]上的最大值为0,则
①当false即false时,false在false上的最小值为1,
因为false图象的对称轴false,所以false,
解得false,符合题意; ………………8分
②当false即false时,false在false上的最大值为1,且false恒成立,
因为false的图象是开口向上的抛物线,在false上的最大值只可能为false或false,
若false,则false,不合题意;
若false,则false,此时对称轴false,
由false,不合题意. ………………11分
综上所述,只有false符合条件. ………………………12分
注:如果先考虑false时,false恒成立,由false,可得false,可以避免讨论,同样得分.
同课章节目录
