人教版八年级数学下册课件-18.1.2 平行四边形的判定4(16张)
文档属性
| 名称 | 人教版八年级数学下册课件-18.1.2 平行四边形的判定4(16张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 169.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 12:16:05 | ||
图片预览




文档简介
人教版数学八年级下册
平行四边形的判定方法
平行四边形的判定
——方法盘点
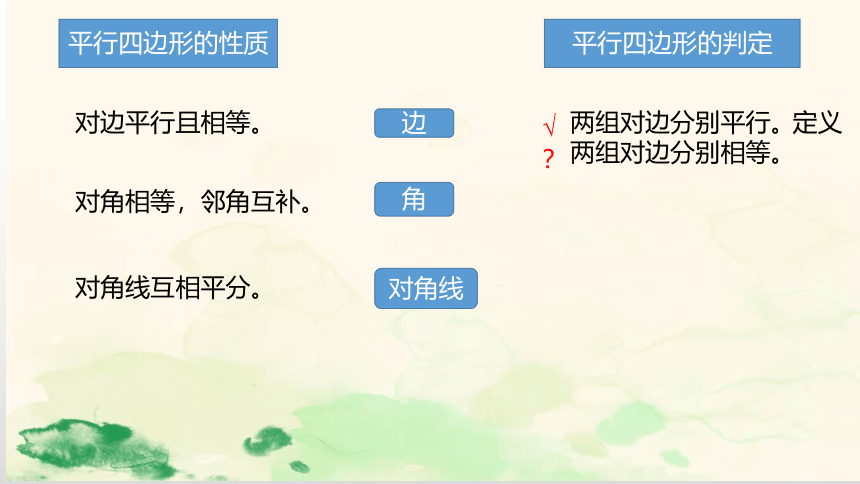
对边平行且相等。
对角相等,邻角互补。
对角线互相平分。
平行四边形的性质
平行四边形的判定
边
角
对角线
两组对边分别平行。
两组对边分别相等。
定义
√
?
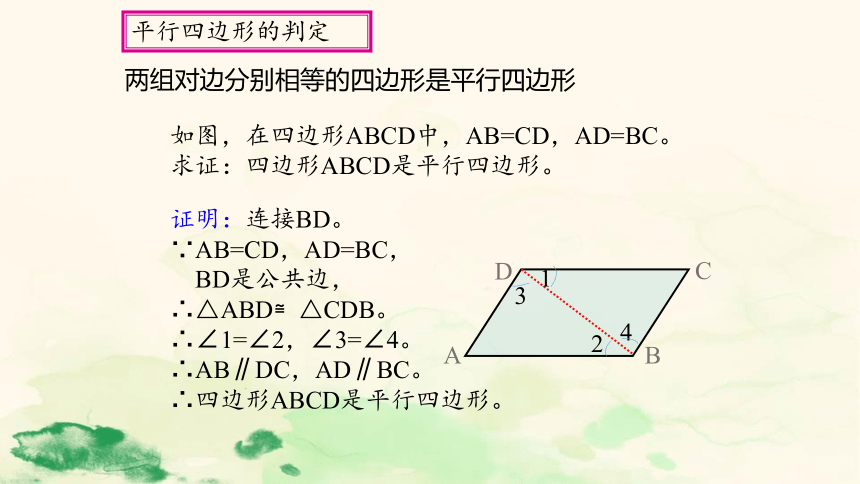
证明:连接BD。
∵AB=CD,AD=BC,
BD是公共边,
∴△ABD≌△CDB。
∴∠1=∠2,∠3=∠4。
∴AB∥DC,AD∥BC。
∴四边形ABCD是平行四边形。
如图,在四边形ABCD中,AB=CD,AD=BC。
求证:四边形ABCD是平行四边形。
平行四边形的判定
D
A
B
C
1
2
3
4
两组对边分别相等的四边形是平行四边形
对边平行且相等。
对角相等,邻角互补。
对角线互相平分。
平行四边形的性质
平行四边形的判定
边
角
对角线
两组对边分别平行。
两组对边分别相等。
定义
√
√
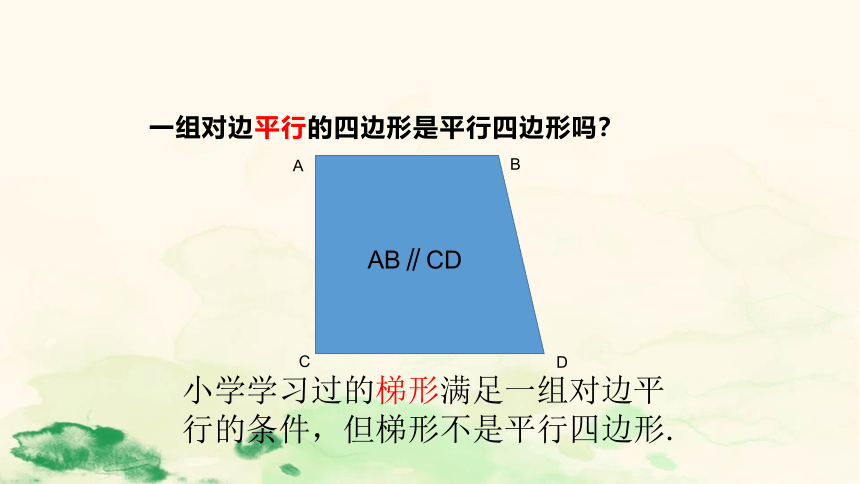
一组对边平行的四边形是平行四边形吗?
小学学习过的梯形满足一组对边平行的条件,但梯形不是平行四边形.
A
B
C
D
AB∥CD
满足一组对边相等的四边形是平行四边形吗?
如图1
,这个四边形EFGH满足一组对边EF=HG相等的条件,但它不是平行四边形.
一组对边平行,另一组对边相等的四边形是平行四边形吗?
AD∥BC且AB=DC,但四边形ABCD不一定是平行四边形。
不一定是,如:等腰梯形
A
B
D
C
AD∥BC
AB=DC
对边平行且相等。
对角相等,邻角互补。
对角线互相平分。
平行四边形的性质
平行四边形的判定
边
角
对角线
两组对边分别平行。
两组对边分别相等。
定义
√
?
一组对边平行且相等。
√
平行四边形的判定
已知:四边形ABCD中AB∥CD且AB=CD.
求证:四边形ABCD是平行四边形。
A
B
C
D
证明:连结AC
∵AB∥CD
∴∠BAC=∠DCA
又∵AB=CD,AC=AC
∴△ABC≌△CDA.
∴BC=AD
∴四边形ABCD是平行四边形。
一组对边平行且相等的四边形是平行四边形
对边平行且相等。
对角相等,邻角互补。
对角线互相平分。
平行四边形的性质
平行四边形的判定
边
角
对角线
两组对边分别平行。
两组对边分别相等。
定义
√
√
一组对边平行且相等。
√
两组对角分别相等。
?
证明:∵ 多边形ABCD是四边形,
∴∠A+∠B+∠C+∠D=360°。
又∵∠A=∠C,∠B=∠D,
∴∠A+∠B=180°,
∠B+∠C=180°。
∴AD∥BC,AB∥DC。
∴四边形ABCD是平行四边形。
如图,在四边形ABCD中,∠A=∠C,∠B=∠D。
求证:四边形ABCD是平行四边形。
平行四边形的判定
D
A
B
C
两组对角分别相等的四边形是平行四边形
对边平行且相等。
对角相等,邻角互补。
对角线互相平分。
平行四边形的性质
平行四边形的判定
边
角
对角线
两组对边分别平行。
两组对边分别相等。
定义
√
√
一组对边平行且相等。
√
两组对角分别相等
对角线互相平分
√
?
如图,在四边形ABCD中,AC,BD相交于点O,且
OA=OC,OB=OD。求证:四边形ABCD是平行四边形。
平行四边形的判定
D
A
B
C
O
证明:∵ OA=OC,OB=OD,∠AOD=∠COB,
∴△AOD≌△COB。
∴∠OAD=∠OCB。
∴AD∥BC。
同理:AB∥DC。
∴四边形ABCD是平行四边形。
对角线互相平分的四边形是平行四边形
对边平行且相等。
对角相等,邻角互补。
对角线互相平分。
平行四边形的性质
平行四边形的判定
边
角
对角线
两组对边分别平行。
两组对边分别相等。
定义
√
√
一组对边平行且相等。
√
两组对角分别相等
对角线互相平分
√
√
谢谢,再见!
平行四边形的判定方法
平行四边形的判定
——方法盘点
对边平行且相等。
对角相等,邻角互补。
对角线互相平分。
平行四边形的性质
平行四边形的判定
边
角
对角线
两组对边分别平行。
两组对边分别相等。
定义
√
?
证明:连接BD。
∵AB=CD,AD=BC,
BD是公共边,
∴△ABD≌△CDB。
∴∠1=∠2,∠3=∠4。
∴AB∥DC,AD∥BC。
∴四边形ABCD是平行四边形。
如图,在四边形ABCD中,AB=CD,AD=BC。
求证:四边形ABCD是平行四边形。
平行四边形的判定
D
A
B
C
1
2
3
4
两组对边分别相等的四边形是平行四边形
对边平行且相等。
对角相等,邻角互补。
对角线互相平分。
平行四边形的性质
平行四边形的判定
边
角
对角线
两组对边分别平行。
两组对边分别相等。
定义
√
√
一组对边平行的四边形是平行四边形吗?
小学学习过的梯形满足一组对边平行的条件,但梯形不是平行四边形.
A
B
C
D
AB∥CD
满足一组对边相等的四边形是平行四边形吗?
如图1
,这个四边形EFGH满足一组对边EF=HG相等的条件,但它不是平行四边形.
一组对边平行,另一组对边相等的四边形是平行四边形吗?
AD∥BC且AB=DC,但四边形ABCD不一定是平行四边形。
不一定是,如:等腰梯形
A
B
D
C
AD∥BC
AB=DC
对边平行且相等。
对角相等,邻角互补。
对角线互相平分。
平行四边形的性质
平行四边形的判定
边
角
对角线
两组对边分别平行。
两组对边分别相等。
定义
√
?
一组对边平行且相等。
√
平行四边形的判定
已知:四边形ABCD中AB∥CD且AB=CD.
求证:四边形ABCD是平行四边形。
A
B
C
D
证明:连结AC
∵AB∥CD
∴∠BAC=∠DCA
又∵AB=CD,AC=AC
∴△ABC≌△CDA.
∴BC=AD
∴四边形ABCD是平行四边形。
一组对边平行且相等的四边形是平行四边形
对边平行且相等。
对角相等,邻角互补。
对角线互相平分。
平行四边形的性质
平行四边形的判定
边
角
对角线
两组对边分别平行。
两组对边分别相等。
定义
√
√
一组对边平行且相等。
√
两组对角分别相等。
?
证明:∵ 多边形ABCD是四边形,
∴∠A+∠B+∠C+∠D=360°。
又∵∠A=∠C,∠B=∠D,
∴∠A+∠B=180°,
∠B+∠C=180°。
∴AD∥BC,AB∥DC。
∴四边形ABCD是平行四边形。
如图,在四边形ABCD中,∠A=∠C,∠B=∠D。
求证:四边形ABCD是平行四边形。
平行四边形的判定
D
A
B
C
两组对角分别相等的四边形是平行四边形
对边平行且相等。
对角相等,邻角互补。
对角线互相平分。
平行四边形的性质
平行四边形的判定
边
角
对角线
两组对边分别平行。
两组对边分别相等。
定义
√
√
一组对边平行且相等。
√
两组对角分别相等
对角线互相平分
√
?
如图,在四边形ABCD中,AC,BD相交于点O,且
OA=OC,OB=OD。求证:四边形ABCD是平行四边形。
平行四边形的判定
D
A
B
C
O
证明:∵ OA=OC,OB=OD,∠AOD=∠COB,
∴△AOD≌△COB。
∴∠OAD=∠OCB。
∴AD∥BC。
同理:AB∥DC。
∴四边形ABCD是平行四边形。
对角线互相平分的四边形是平行四边形
对边平行且相等。
对角相等,邻角互补。
对角线互相平分。
平行四边形的性质
平行四边形的判定
边
角
对角线
两组对边分别平行。
两组对边分别相等。
定义
√
√
一组对边平行且相等。
√
两组对角分别相等
对角线互相平分
√
√
谢谢,再见!
