苏科版七年级数学下册第七章平面的图形认识(二)复习二(Word版 无答案)
文档属性
| 名称 | 苏科版七年级数学下册第七章平面的图形认识(二)复习二(Word版 无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 140.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-17 12:19:04 | ||
图片预览

文档简介
苏科版七年级数学下册第七章平面的图形认识(二)复习二
一:学习目标
熟练运用平行线的性质和判定、三角形内角和定理熟练
掌握平行线和三角形中的基本图形
二、学习过程
(一)、基本应用
1.一个多边形的边数每增加一条,这个多边形的--------------------------------(
)
A.内角和增加360°
B.外角和增加360°
C.对角线增加一条
D.内角和增加180°
2、满足下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C
B.∠A=2∠B=3∠C
C.∠A:∠B:∠C=2:3:1
D.
一个外角等于和它相邻的内角
3、三角形的三条高相交于一点,此一点定在(
)
A.
三角形的内部
B.三角形的外部
C.三角形的一条边上
D.
不能确定
4、下列结论正确的是
…………………………………………(
)
A.两直线被第三条直线所截,同位角相等
B.三角形的一个外角等于两个内角的和
C.任一多边形的外角中最多有三个是钝角
D.连结平面上三点构成的图形是三角形
解决问题1、平行线中基本图形的应用
1、 如图所示,已知AB∥CD,分别探索下列三个图形中∠P与∠A,∠C的关系,请你从所得的三个关系式中任选一个加以说明.
结论:①
②
③
解决问题2:三角形中基本图形应用
1、如图所示,∠A=∠C=30°,∠D=90°,则∠ABC
.
2、△ABC中,BP、CP分别是∠ABC与∠ACB的平分线,BP、CP交△ABC内一点P.∠A=50°时,求∠P的度数;
变化1、
BP、CP分别是∠ABC与∠ACD的平分线,求∠P的度数;
变化2、BP、CP分别是∠EBC与∠BCD的平分线,求∠P的度数;
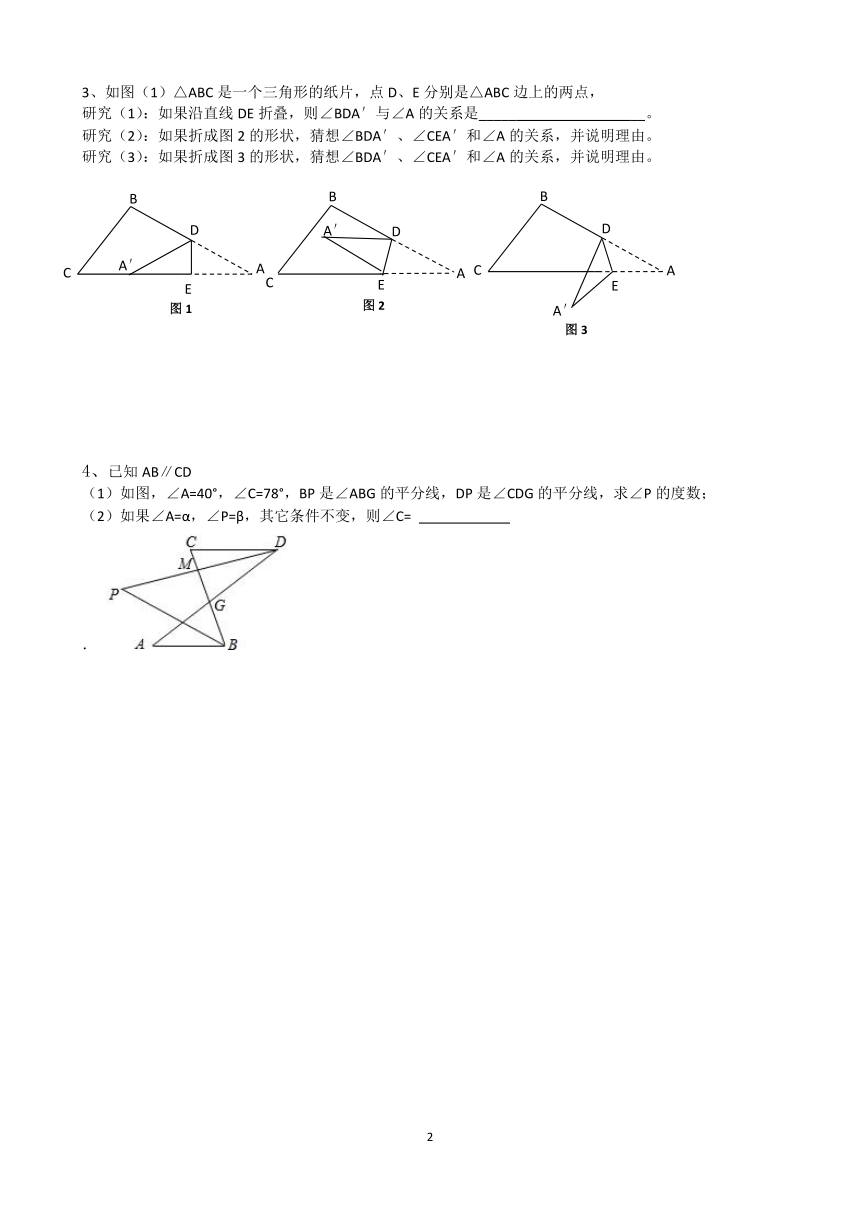
3、如图(1)△ABC是一个三角形的纸片,点D、E分别是△ABC边上的两点,
研究(1):如果沿直线DE折叠,则∠BDA′与∠A的关系是_____
__。
研究(2):如果折成图2的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由。
研究(3):如果折成图3的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由。
(
A
A′
B
E
D
C
图3
)
(
C
B
A
A′
D
E
图2
)
(
A
A′
B
E
D
C
图1
)
4、已知AB∥CD
(1)如图,∠A=40°,∠C=78°,BP是∠ABG的平分线,DP是∠CDG的平分线,求∠P的度数;
(2)如果∠A=α,∠P=β,其它条件不变,则∠C=
.
1.如图,把ΔABC沿线段DE折叠,使点A落在点F处,BC∥DE,若∠B=50°,则∠BDF=____0.
(
第2题
A
B
E
D
C
)
(
第1题图
)
(
第3题
)
2.如图,在△ABC中,AD是高,AE是角平分线,∠B=20?,∠C=60?,则∠EAD=______°.
3.如图所示,分别以边形的顶点为圆心,以1cm为半径画圆,则图中阴影部分的面积之和为
.
(
(第6题图)
)4、如图,∠ABD,∠ACD的角平分线交于点P,若∠A=50°,∠D=10°,则∠P的度数为
5、如图,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC外,若∠2=20°则∠1的度数为
度
6、如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=,则∠C的度数为(
)(A)
40°
(B)
41°
(C)
42°
(D)
43°
7.如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为( )
A.120°
B.135°
C.150°
D.180°
8、如图所示,把一个四边形纸片ABCD的四个顶角分别向内折叠,折叠之后,4个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8的度数是
( )
A.540°
B.630°
C.720°
D.810°
9、如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=80°,则∠BFD=
度.
10、如图①是长方形纸带,将纸带沿EF折叠成图②,再沿BF折叠成图③.
(1)若∠DEF=200,则图③中∠CFE度数是多少?
(
A
E
B
F
C
D
图
③
A
E
B
F
C
D
图
②
A
E
B
F
C
D
图
①
)
(2)若∠DEF=α,把图③中∠CFE用α表示.
11、Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2=_____°;
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间有何关系?
(3)若点P在Rt△ABC斜边BA的延长线上运动(CE<CD),则∠α、∠1、∠2之间有何关系?猜想并说明理由.
12、已知:∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.设∠OAC=°
(1)如图1,若AB∥ON,则:
①∠ABO的度数是
;
②如图2,当∠BAD=∠ABD时,
;
(
备用图
)(2)如图3,若AB⊥OM,则是否存在这样的的值,使得△ADB中有两个相等的角?若存在,求出的值;若不存在,说明理由.(画图探究)
1
一:学习目标
熟练运用平行线的性质和判定、三角形内角和定理熟练
掌握平行线和三角形中的基本图形
二、学习过程
(一)、基本应用
1.一个多边形的边数每增加一条,这个多边形的--------------------------------(
)
A.内角和增加360°
B.外角和增加360°
C.对角线增加一条
D.内角和增加180°
2、满足下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C
B.∠A=2∠B=3∠C
C.∠A:∠B:∠C=2:3:1
D.
一个外角等于和它相邻的内角
3、三角形的三条高相交于一点,此一点定在(
)
A.
三角形的内部
B.三角形的外部
C.三角形的一条边上
D.
不能确定
4、下列结论正确的是
…………………………………………(
)
A.两直线被第三条直线所截,同位角相等
B.三角形的一个外角等于两个内角的和
C.任一多边形的外角中最多有三个是钝角
D.连结平面上三点构成的图形是三角形
解决问题1、平行线中基本图形的应用
1、 如图所示,已知AB∥CD,分别探索下列三个图形中∠P与∠A,∠C的关系,请你从所得的三个关系式中任选一个加以说明.
结论:①
②
③
解决问题2:三角形中基本图形应用
1、如图所示,∠A=∠C=30°,∠D=90°,则∠ABC
.
2、△ABC中,BP、CP分别是∠ABC与∠ACB的平分线,BP、CP交△ABC内一点P.∠A=50°时,求∠P的度数;
变化1、
BP、CP分别是∠ABC与∠ACD的平分线,求∠P的度数;
变化2、BP、CP分别是∠EBC与∠BCD的平分线,求∠P的度数;
3、如图(1)△ABC是一个三角形的纸片,点D、E分别是△ABC边上的两点,
研究(1):如果沿直线DE折叠,则∠BDA′与∠A的关系是_____
__。
研究(2):如果折成图2的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由。
研究(3):如果折成图3的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由。
(
A
A′
B
E
D
C
图3
)
(
C
B
A
A′
D
E
图2
)
(
A
A′
B
E
D
C
图1
)
4、已知AB∥CD
(1)如图,∠A=40°,∠C=78°,BP是∠ABG的平分线,DP是∠CDG的平分线,求∠P的度数;
(2)如果∠A=α,∠P=β,其它条件不变,则∠C=
.
1.如图,把ΔABC沿线段DE折叠,使点A落在点F处,BC∥DE,若∠B=50°,则∠BDF=____0.
(
第2题
A
B
E
D
C
)
(
第1题图
)
(
第3题
)
2.如图,在△ABC中,AD是高,AE是角平分线,∠B=20?,∠C=60?,则∠EAD=______°.
3.如图所示,分别以边形的顶点为圆心,以1cm为半径画圆,则图中阴影部分的面积之和为
.
(
(第6题图)
)4、如图,∠ABD,∠ACD的角平分线交于点P,若∠A=50°,∠D=10°,则∠P的度数为
5、如图,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC外,若∠2=20°则∠1的度数为
度
6、如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=,则∠C的度数为(
)(A)
40°
(B)
41°
(C)
42°
(D)
43°
7.如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为( )
A.120°
B.135°
C.150°
D.180°
8、如图所示,把一个四边形纸片ABCD的四个顶角分别向内折叠,折叠之后,4个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8的度数是
( )
A.540°
B.630°
C.720°
D.810°
9、如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=80°,则∠BFD=
度.
10、如图①是长方形纸带,将纸带沿EF折叠成图②,再沿BF折叠成图③.
(1)若∠DEF=200,则图③中∠CFE度数是多少?
(
A
E
B
F
C
D
图
③
A
E
B
F
C
D
图
②
A
E
B
F
C
D
图
①
)
(2)若∠DEF=α,把图③中∠CFE用α表示.
11、Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2=_____°;
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间有何关系?
(3)若点P在Rt△ABC斜边BA的延长线上运动(CE<CD),则∠α、∠1、∠2之间有何关系?猜想并说明理由.
12、已知:∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.设∠OAC=°
(1)如图1,若AB∥ON,则:
①∠ABO的度数是
;
②如图2,当∠BAD=∠ABD时,
;
(
备用图
)(2)如图3,若AB⊥OM,则是否存在这样的的值,使得△ADB中有两个相等的角?若存在,求出的值;若不存在,说明理由.(画图探究)
1
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
